效率与公平视角下企业及政府的资源配置决策

曾 倩，韩 珣，方 新

(1. 重庆工商大学管理科学与工程学院，重庆 400067；2. 四川警察学院道路交通管理学，四川 泸州 646000)

1 引言

资源配置决策需要对有限资源进行合理安排，广泛涉及医疗、收入分配等制度安排[1]，学校、医院等公共资源，生产设备、工人等企业资源在数量、时间和空间上的配置[2]。效率和公平是资源配置中的两个重要目标。在“经济人”假设下人们总是追求效率的最大化，即强调资源的产生的总效用最大。由于个体的资源投入产出比不同，追求效率通常意味着个体获得资源的不均等[3]。Binmore[4]认为公平是人类天生的追求，不公平将会导致个体效用的降低。大量的行为实验研究也表明，人是具有公平偏好的，存在公平对待他人以及得到公平对待的意愿[5]。

企业与政府都是资源配置的主体，在现实经济活动中，关注公平目标的通常是政府，企业仍以效率为主。例如，2017年我国每千人口床位数城市为8.29张，农村仅为3.73张，基层医疗机构床位有98.6%为公立性质；邮政快递网点行政村覆盖率达87%，而民营快递企业农村布点仅限于发达乡镇。近年来，关于“企业社会责任”的研究指出，企业行为对社会资源优化配置有决定性的影响，仅追求效率无法实现社会福利最大化[6]。“公共服务市场化”的相关研究也表明，市场应更多地参与到公共服务资源的配置中[7]。政府和企业在资源配置中各自追求的目标是什么？企业会不会考虑公平？二者的决策结果是否有差异？都是值得探讨的问题。

已有文献中企业关注公平更多地集中在供应链领域，以订货批量、定价或协调契约问题为主。Bolton[8]最早刻画了公平关切形式，认为效用的正负差异都会带来一定的损失。Loch和Wu[9]提出公平关切效用形式Ui=πi+θiπj，其中θi为公平关切参数，反映了参考点效用对己方效用的影响。选择的参考点通常包括相对效用、绝对效用、其它均衡状态下的效用等。例如，魏强和李胜[10]在研究纵向供应链定价问题时，将供应商的相对效用作为零售商公平偏好的参考点。王玉燕和李璟[11]将制造商效用作为网络平台公平偏好参考点，研究了不同主导模式下E-闭环供应链的定价与服务水平。张旭和张庆[12]将Nash讨价还价解中零售商利润作为参考点，建立Stackelberg博弈模型。

部分研究关注了企业资源配置中的公平，多考虑企业员工的公平感受或设备的负荷均等。Jütte等[13]将员工间两两比较的不满意度差值作为公平测度指标，总成本作为效率指标构建了多目标排班模型。Bonald等[14]引入公平参数α建立效用函数，探讨缓存网络能力的均衡分配问题。仅有较少的研究考虑了下游客户公平感受对企业资源配置决策的影响。例如，Chung等[15]构造需求公平约束、流量公平约束建立了电动车充电站在各区域的数量分配模型。Bertsimas等[16]在等待成本函数中增加了航空公司的公平厌恶损失，探讨了机场的跑道时间分配问题。

在政府资源配置研究中，公平是学者们广泛关注的目标，研究的内容主要集中于公共资源分配、公共设施选址等方面。在20世纪80年代，Varian[17]就提出了效率与公平问题，强调了生产与分配中公平的重要性。在资源分配领域，研究主要包括数量和能力的分配，最早及最广泛的应用为通信带宽分配，后扩展到水资源、医院床位、应急物资、碳排量等[18]。Zhou Liping等[19]考虑到达和等待时间的公平性，建立了医院床位分配的公平与收益多目标随机规划模型。Gutjahr和Fischer[20]采用基尼系数衡量损失成本的公平性，研究了人道物流服务能力分配问题。在设施选址领域，学者们通常探讨如医院、学校等公共设施的选址，将到达设施的时间或距离作为影响公平感知的关键因素。Suzuki和Drezner[21]以最大服务距离最小刻画了公共设施选址公平。Batta等[22]加入距离设施点的上界约束，建立了P中值选址模型。Romero等[23]以基尼系数衡量各人口集聚区到设施距离的差异性，建立了危险品存储点选址和路径优化模型。

现有研究中实现公平的主要方法有三种。一是构造基于公平准则的目标函数，常见准则有最大最小公平、比例公平、纳什讨价还价公平等[14,16,21]。二是增加公平约束，如设施点距离的上界约束、服务满意度的下界约束等[15,22]。三是引入公平测度指标构造效率与公平的多目标函数，常见公平指标有基尼系数、极差、标准差、阿特金森指数等[13,19,20,23,24]。这些测度指标主要从统计学的角度研究了个体效用的差距，并不能很好地反应个体考虑公平的动机。因此Espejo和Puerto[25]提出了“客户嫉妒”的概念，与供应链公平关切下的参考点依赖类似，通过个体与他人比较产生的嫉妒值衡量资源配置公平性。但其研究仅考虑了公平目标，没有研究同时考虑效率时，嫉妒值如何影响决策者的总效用。

综上，现有研究主要存在三方面不足。一是考虑公平的资源配置研究中往往没有界定决策的主体，或者简单地将政府作为单一决策机构，忽略了企业在社会资源配置中的主体作用，也没有比较不同主体的资源配置决策行为是否存在差异；二是企业考虑的公平大多关注供应链上下游或内部资源使用的均衡，较少有研究探讨公平偏好对个体效用(如服务水平、消费者满意度)的影响；三是公平测度指标的选择与目标函数的构建，难以客观反映企业和政府的决策目标与偏好。

鉴于此，本文从企业和政府两个决策主体出发，探讨了“谁在什么情况下会考虑怎样的效率与公平”这一基本问题。与已有研究相比，本文将单一主体扩展为两个主体，对比分析了二者效率与公平偏好的不同动因与内涵；改进了现有模型，引入“个体变权”和“客户嫉妒”分别构建政府和企业的多目标效用函数，更具针对性地体现了政府对社会总福利的综合考虑、客户公平偏好对企业效用的影响；最后，比较了企业和政府在不同公平偏好情景下的最优资源配置决策，为政府协调与激励政策的制定、“公共服务市场化”由定性到定量的研究提供理论支撑。

2 资源配置决策模型

2.1 问题描述

企业和政府的资源配置决策为X，即资源数量分配、设施选址、设备能力配置、排班计划等。个体在资源配置决策X下获得效用ui(X)，i=1,2,…,n[3,16]。个体i实际需求量为Di，接受服务的需求量di与效用ui正相关，获得效用越高，个体接受服务的需求量越接近实际需求量。个体效用的提高将增加成本投入，k为提高效用的成本参数，C为成本投入约束。单位需求获得收益为p，由于个体区位、交通等条件差异，服务个体时的单位需求成本ci不同。在考虑客户与决策者公平偏好的情况下，企业和政府应如何决定个体获得的效用ui，以实现各自的效率与公平目标。

2.2 个体效用与需求量

由于资源配置涉及分配、选址、排班等广泛的问题，仅用资源数量难以表现配置结果。因此本文将个体效用作为决策变量，以衡量资源配置决策对个体的影响。例如，在应急物资分配决策下各区域获得的资源数或满意度，在公共选址决策下居民到设施点的距离、时间或成本等。

个体对获得的效用通常存在一定要求，效用过低时，资源配置结果低于预期，将导致需求的损失。因此，本文中个体接受服务的需求量di受本身实际需求量Di及获得效用ui的影响。当获得效用高于特定值Umax时，di等于实际需求Di。否则，将损失部分需求，直到效用低于特定值Umin时，个体将由于不满退出系统，此时需求量为0。因此，个体接受服务的需求量为：

(1)

2.3 效率与公平目标

1) 企业决策中的效率与公平

企业追求的效率通常为成本最低、利润最高或服务质量最优等。本文以利润最高为效率目标，即服务总收益与总成本的差值最大，可表示为：

(2)

企业考虑公平一方面来自于决策者公平对待他人的偏好，另一方面来自于客户获得公平对待的要求。由于客户感知到不公平时，可能出现减少需求、退出系统或其它报复行为，会对企业收益产生较大影响[9]。例如，航空公司在对机场的跑道分配感到不公平时，有可能改变下阶段的航线计划，选择其它的起降机场[16]。零售商对供应商产能分配感到不公平时，可能出现报复行为，减少订购量[26]。因此，相较而言，避免客户公平偏好带来的损失是企业考虑公平更重要的动因。

由于个体的公平感知往往是与他人比较获得的，Espejo和Puerto[25]提出了“客户嫉妒”的概念，与供应链公平关切下的参考点依赖[9-12]类似，通过比较产生的嫉妒值衡量资源配置公平性。相较于基尼系数、方差等其它统计概念上的常用指标，嫉妒值更加直观地反映了实际生活中个体对公平的感知与判断。但其研究中仅以最小嫉妒值为单一目标，没有研究效率与公平多目标的情况。本文在考虑效率的同时，采用客户需求损失值量化了个体公平偏好对企业效用的影响。

当个体i的效用与j相比较低时，i产生嫉妒gij，嫉妒值为个体效用差值，反之嫉妒为0，gij=max(0,uj-ui)。假设所有个体对不公平的厌恶程度相同，即可接受的最大嫉妒值均为α。当客户感知到嫉妒时，对企业服务产生不满，导致企业效用的损失；当个体i的总嫉妒超过可接受最大嫉妒值时，个体将退出系统，企业服务个体i获得的效用降为0，即服务利润等于不公平负效用。可计算损失参数为：

(3)

因此，企业的公平目标可表示为不公平导致的负效用最小，即：

(4)

2) 政府决策中的效率与公平

政府考虑的效率与公平内涵和企业不同。效率方面，政府通常希望更多的个体获得服务，以最大覆盖为目标，追求总实际需求量最大，即：

(5)

公平方面，政府决策同样受决策者自身公平偏好，以及社会公众公平偏好的共同影响。由于政府配置的通常为公共服务资源，需要综合考虑社会稳定、经济发展等多方面的因素，因此政府自身的公平偏好往往是资源配置决策的主要动因。政府要尽可能的保障弱者利益，公平目标通常为最小的个体效用最大化，即：

maxz4=minui,i=1,2,…,n.

(6)

2.4 企业决策模型

考虑客户公平偏好带来的需求损失，结合式(2)、(4)构建企业资源配置决策模型如下：

(7)

s.t.

(8)

di≤Di,i=1,2,…,n,

(9)

(10)

gij≥uj-ui,i,j=1,2,…,n,

(11)

ui≥Umin,di≥0,gij≥0,i,j=1,2,…,n,

(12)

其中，式(7)为目标函数，α取值不同，企业的效率与公平目标不同。当α为足够大的数时，个体对嫉妒的容忍值高，不公平产生的负效用为0，此时为完全效率目标；当α=0时，个体不能容忍嫉妒，此时为完全公平目标；当α取其它值时表示实现一定程度的公平。式(8)、(9)表示个体接受服务的需求量约束，式(10)表示提高获得效用的总成本约束，式(11)表示个体的嫉妒值，式(12)为变量的下界约束。

该模型结合了企业利润函数与基于“客户嫉妒”的不公平负效用函数，刻画了客户公平偏好对企业决策的影响机制。

2.5 政府决策模型

考虑政府自身公平偏好，结合式(5)、(6)，采用文献[27]中的变权方法构造政府的资源配置决策模型如下：

(13)

s.t.

式(8)～(10)、式(12)

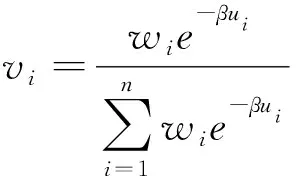
该模型利用个体权重体现了政府资源配置中的两层偏好。一方面初始权重的设置可体现政府对不同个体的资源倾斜，如部分欠发达或亟需扶持地区；另一方面公平参数的设置体现了政府对弱势个体的重视程度，即对社会公平的偏好。

2.6 公平参数的选择

由于追求公平会导致效率的损失，在实际的资源配置决策中，企业和政府需要决定实现何种程度的公平，即在效率与公平目标中作出权衡[3]。

企业考虑公平主要源于对自身效用损失的规避，因此公平参数体现为客户的公平偏好。在三种场景下客户倾向于拥有较高公平偏好：一是对比可见场景，即客户能快速、清晰地感知到与其他个体效用的区别，如大部分的排队场景；二是重要资源的配置场景，如应急物资的分配中，客户更希望获得公平的对待；三是外生权利场景，即对于教育、医疗、安全等个体应当公平享有的外生权利，资源配置的公平要求更高[28]。由于客户的个体公平偏好为外生参数，取值并不由企业自身决定，因此企业可通过市场调查、行为实验等方式获得特定情境下客户服务选择行为结果，以分析其公平偏好。

政府考虑公平主要源于维护社会稳定、促进区域发展的职责需要，因此公平参数体现为决策者自身的公平偏好。本文认为以下三种情况下，政府通常拥有较高的公平偏好：一是区域发展失衡，需要促进落后地区的发展。例如在城乡资源配置中，农村地区的资源投入产出效率往往偏低，在效率目标下无法保障有效的资源供给，此时政府倾向于向农村地区配置更多的资源。二是社会矛盾突出，需要维护社会稳定。例如在多民族、多宗教的地区，资源的配置应当更加公平。三是保障公民的基本权利，例如教育、医疗等公共资源的配置。由于政府的公平偏好为内生变量，需要对其进行选择以权衡效率与公平，采用基于损失偏好的效率与公平权衡方法[29]。

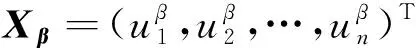
(14)

(15)

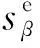
3 变分不等式转化

由于目标函数连续可微，本文利用最优化问题与变分不等式之间的转换关系，将最优化问题改写成变分不等式形式。

带约束的最优化问题为：

(16)

s.t.

(17)

xi∈Ki,i=1,2,…,n,

(18)

(19)

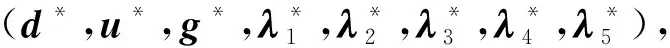
(20)

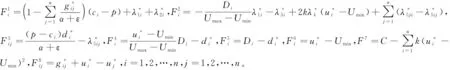
同理，可将政府决策模型转化为变分不等式形式。

4 修正投影算法求解

修正投影(Modified Projection)算法是对投影算法的改进，提出了更一般的下降方向，在每步迭代中增加一个投影步，以克服投影算法对参数估计的依赖[30]。设t为迭代数，修正投影算法可描述为

(21)

为验证修正投影算法(MP)的有效性，设计10组不同规模算例，比较在不同的企业、政府公平参数下MP算法与MATLAB非线性规划工具箱Fimincon的SQP算法结果。算法均利用MATLABR2014a软件，在InterCorei3-550@ 3.20 Hz CPU，4.00 GB内存电脑上运算。采用阿里云天池“最后一公里极速配”数据，选取上海的配送点作为需求点，需求点个数n取200，400，600，800，1000。随机生成每个需求点的日均需求量di∈[0,100]。个体的单位服务成本ci，可通过需求点到最近的配送中心距离估算得到。单位需求的收益p=2，增量服务成本系数k=0.05。决策变量为个体效用，此处为配送时效，最慢的服务时效为36小时，最快服务时效为6小时，时效值越低说明个体效用越高。因此，最高个体效用Umax=36，最低个体效用Umin=6。α/n表示客户可容忍个体效用与其他个体平均差值，取10和100个小时。β取0，1表示政府的公平参数，δ为修正投影算法计算参数。比较目标函数值和运算时间，如表1所示。

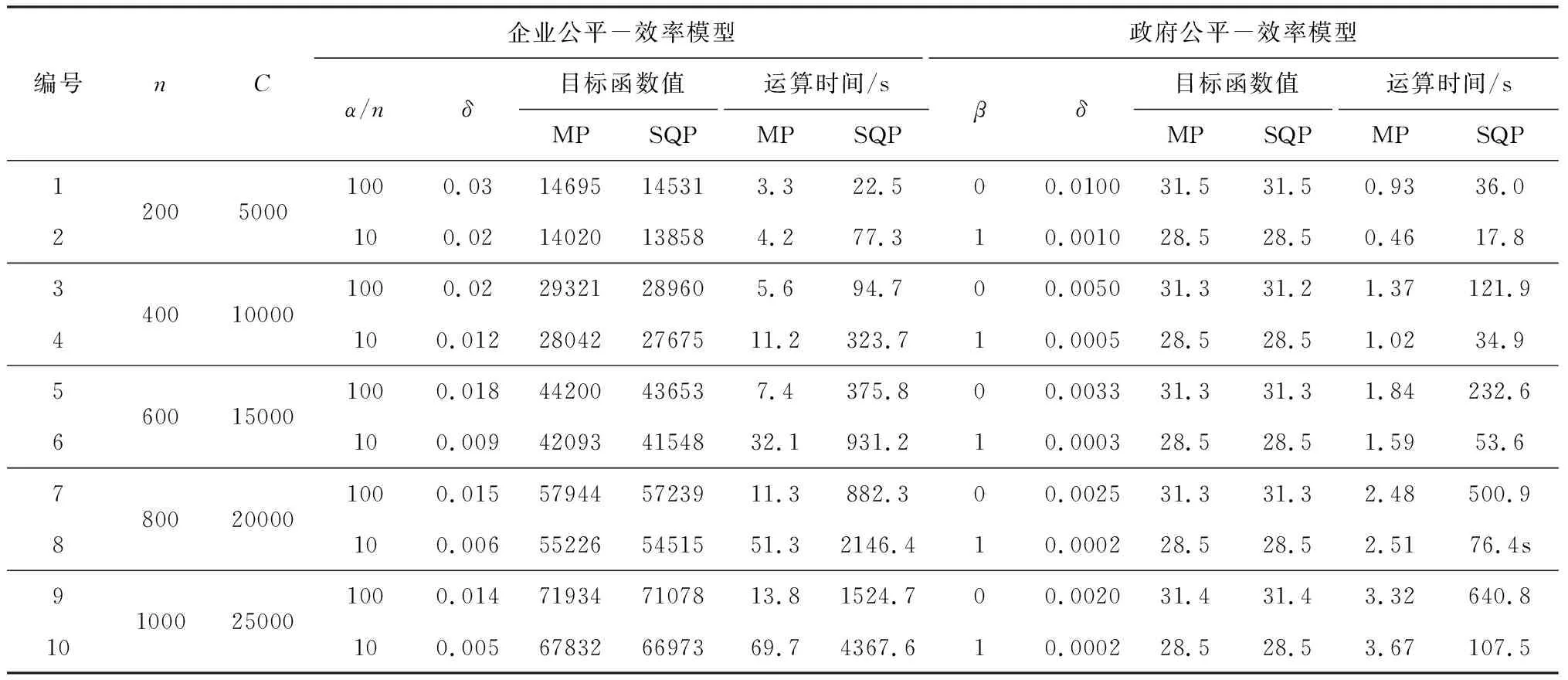
表1 算法结果比较

MP算法在运算时间上有显著的优越性，随着计算规模的增大，计算时间的差距越明显。在目标函数值上，企业决策模型采用MP算法的结果相对优于SQP算法，政府决策模型二者结果基本一致。综上，采用变分不等式求解企业与政府的资源配置决策模型，无论是在求解精度还是在求解效率上都具有一定优势，尤其是在大规模计算时，算法优势更加显著。

5 算例分析

为了更好地分析公平参数对企业和政府决策模型的影响，设计小规模算例n=20，增量成本约束C=500，其它参数设置同上。将企业、政府的决策模型转化为变分不等式后，通过修正投影算法求解不同公平参数下的最优方案，探讨不同公平偏好对企业和政府决策的影响。

1) 企业决策结果

企业公平参数是客户对嫉妒的最大容忍值，分别取α=0、200、400、600、1000000。个体最优个体效用变化情况如表2所示。

表2 不同公平参数下企业最优个体效用差异分析

随着客户对公平性要求的提高，个体效用两极分化现象反而愈发显著。当α=1000000时，客户对公平性不敏感，个体的个体效用与客户价值μi=(p-ci)Di呈正相关，即个体的服务成本越低、实际需求越大，获得的个体效用越高。随着客户不公平容忍程度的降低，企业将优先保障μi较高的个体获得相近的个体效用，同时牺牲μi较小个体的利益。当α=0时，客户极端在意公平，个体间个体效用极差达到最大，部分需求点个体效用全部为最高，其它则全部为最低。

个体利润与嫉妒值的变化随μi值由大到小可分为四类，如图1所示。①μi值极高的个体，利润和嫉妒值基本不变。无论α取值如何，此类个体的效率与公平性总是优先得到保障，如需求点2、5、6等。②μi值较高的个体，利润增加且嫉妒值减少。此类个体由于不公平带来的损失相对较高，因此获得了与μi值极高个体一样的个体效用，效率与公平性都有所提升，如需求点9、18。③μi值较低的个体，利润先增后减，嫉妒值先降后升。此类个体在效用逐渐两极分化的过程中，先是被归为优先保障的个体，之后则被牺牲以换取更高μi个体的公平性，因此效率与公平的表现呈现先改善后降低的趋势，如需求点11、14、16。④μi值极低的个体，利润变化不大但嫉妒值增加。此类个体始终维持在较低的个体效用，因此利润变化不大，但由于其它个体的个体效用提升，导致嫉妒值增加，如需求点1、3、4等。

2) 政府决策结果

随着政府公平参数β的增加，总的实际需求量减少而最低个体效用增加，说明效率降低但公平性增加，如图2(a)所示。当β=0时，总实际需求达到最大932，最低个体效用也最低为8.4，说明此时决策结果效率最优但公平性较差。当β∈[0,0.2]时，效率与公平值的变化明显，之后逐渐放缓。β≥1后效率与公平值基本保持不变。当β=2时总实际需求降低至835，最低个体效用提高至27.8。总体来看，较小的效率损失可换得较高的公平损失，如图2(b)所示。当政府偏好于效率，倾向由市场发挥资源配置作用时，可设置较低的效率损失容忍值。如当δe=3%时，政府可选择的最优公平参数β=0.04，公平损失为52%。当政府偏好于公平，对社会公平和地区平等发展要求更高时，可设置较高的效率损失容忍值。如当δe=10%时，政府最优公平参数β=0.8，此时公平损失降低为5%。

图2 不同公平参数β下政府决策结果

3) 企业与政府决策结果对比

由于企业和政府的公平目标分别受客户公平偏好α与政府公平偏好β的影响，主要有以下四种偏好组合情景。一是高α、高β的情景Shh，在实际生活中主要体现在教育、医疗、交通等公共资源的配置上，无论是客户还是政府都有较高的公平要求。二是高α、低β的情景Shl，例如在餐饮、零售等具有排队特征的可见对比场景下，客户对不公平的待遇有非常直接的感受，对公平更加敏感，而政府的公平偏好相对较低。三是低α、高β的情景Slh，例如金融、科研技术服务、文化体育等社会资源的配置，客户的公平感知相对教育、医疗资源而言并不强烈，但这些资源对地区经济和文化发展至关重要，因此政府可能存在较高的公平偏好。四是低α、低β的情景Sll，此时客户和政府都认可效率是决定资源配置的关键因素，如高端零售、文娱、旅游等消费市场。

在Shl和Slh情景下，企业与政府的决策行为具有较大差异是显而易见的，因此主要比较Sll和Shh情景。公平参数(α,β)取值分别为(1000000,0)、(0,2)，资源配置结果见表2、图2。可知，在Sll情景下企业与政府均追求效率最优，二者资源配置结果差异不大。在Shh情境下企业与政府均追求公平最优，二者配置结果差异较大，企业呈现显著的两极分化，而政府决策中个体的个体效用基本相同。不同主体决策结果的效率与公平表现，如表3所示。

表3 企业与政府决策的效率与公平比较

在总利润和总实际需求两个效率指标上，企业与政府的效率最优决策差异不大，其次表现较好的为企业的公平最优决策，而效率损失最大的是政府的公平决策。在总嫉妒和最低个体效用指标上，企业追求公平最优时反而公平表现最差，因为此时企业决策中两极分化最为显著，而政府公平最优结果的公平表现非常突出，基本实现了个体效用的均等。

6 结语

本文从企业和政府两个决策主体出发，分别构建效率与公平权衡的资源配置决策模型。将客户的公平偏好作为企业考虑公平的主要动因，通过计算基于客户嫉妒的不公平损失，结合利润目标构建企业多目标模型。将维护社会公平与稳定作为政府考虑公平的主要动因，以个体最小效用最大化为公平目标，服务覆盖最大为效率目标，引入变权方法构建政府决策模型。在此基础上，提出基于客户与决策者偏好的公平参数选择方法，运用实际算例分析了企业与政府的决策行为差异，以及公平参数对结果的影响。

研究结果表明，随着客户公平偏好的增加，企业将优先保障高价值个体间的公平，牺牲低价值个体的利益，资源配置的分化特征愈发显著。随着政府决策者公平偏好的增加，效用越低个体在决策中的权重越大，所有个体间的资源配置结果越均等。可见，企业与政府决策行为存在较大差异，在此基础上可拓展公共资源配置中政府对企业的补贴政策研究。