教育层次结构对产业结构优化升级的影响研究
——基于空间杜宾模型①
2020-11-20
(晋城职业技术学院财经系,山西晋城 048000)
判断一个国家或地区产业结构调整变化是否是产业结构优化,除了需要考虑经济效率之外,还需要考虑充分就业、环境等基本因素,尤其针对我国是人口大国的现状,产业结构优化是否有利于充分就业,也是当前需要考虑的非常重要的因素。目前我国经济从高速增长阶段转为高质量发展阶段,重中之重是产业结构的调整优化,主导产业将由劳动密集型产业转向资本技术密集型产业,这必然会对我国就业产生影响。与此同时,教育的规模和结构决定了人力资本的生产效率和创新能力,从而对产业结构优化升级产生重要影响,尤其是人力资本教育层次结构的变化与产业结构优化趋势是否匹配决定着产业结构优化效率,同时也是促进就业的重要路径。在这个背景下,关于人力资本与产业结构优化、产业结构优化与就业之间相互关系再次引起了关注,本文拟在促进就业目标下实证分析我国区域间不同教育层次的人力资本对产业结构优化升级的影响效应,在此基础上,提出各区域如何发展不同层次教育来促进本地区人力资本对产业结构优化调整推动作用的思路和对策。
一、文献评述
近年来,国内学者对人力资本、产业结构和就业之间的关系进行了大量研究,目前这些文献主要关注两个方面:
一是人力资本与产业结构之间的关系,大多数文献是从人力资本存量角度进行论证。主要文献有:张少红[1]提出劳动力素质的高低直接影响着产业结构优化升级的速度。冉茂盛和毛战宾[2]、靳卫东[3]从理论角度论证了人力资本能够促进产业结构优化。闵维方和蒋承[4]等通过构建产业结构、经济发展和人力资本存量的三维结构,认为调整产业结构需要优化人力资本的教育结构,二者具有引领和适应的双重关系,在当今经济发展过程中应有效、持续地发挥教育的先导作用。近年来,国内学者开始更多采用现代计量经济学模型进行实证研究。欧阳峣和刘智勇[5]基于异质性与适应性视角,以中国为样本,通过采用耦合度模型论证发展中大国人力资本与多元化的产业结构具有很高的匹配程度。赵楠[6]以2002—2012 年我国30 个省市级数据为例,通过采用空间面板数据模型论证我国农村劳动力流动对产业结构调整的影响方向与力度。孙海波和焦翠红[7]以我国2003—2013 年的30 个省市级面板数据为例,通过构建面板平滑转换模型论证人力资本集聚对产业结构升级的影响。
二是产业结构与就业之间关系的研究。国外较早地开始研究产业结构与就业变动关系的代表性理论有配第⁃克拉克定理、刘易斯的二元经济理论、拉尼斯⁃费景汉和乔根森的人口流动模型、新制度经济学派中的制度变迁理论等,这些理论为后期研究产业结构和就业之间关系提供了重要理论基础。此后,国外学者采用一些计量模型方法对英国、美国、日本等国家进行实证研究,例如,Iwao[8]以日本在1955—1968 年的经济发展模式为例,理论研究了产业发展模式与就业结构的相互关系;Juleff[9]以1971—1989 年英国为例,论证英国经济发展的同时,第一产业和第二产业就业人数所占比重大幅下降,而第三产业就业人数比重大幅增长,尤其是服务业就业人数增长最为显著。
国内学者研究就业与产业结构关系始于20 世纪90 年代。近年来,国内学者的相关研究主要关注在两个方面:一是产业结构与就业之间的作用机制。例如,王旭升和王旭辉[10]、詹浩勇[11]研究了我国在重化工业阶段重化工业对就业的影响效应,认为我国重化工业发展对就业的直接效应是会引起第二产业就业弹性下降,降低了吸纳劳动力就业的能力。孙晶和蒋伏心[12]、丁一兵等[13]从资本市场的视角研究产业结构与就业的运行机制,他们认为资本市场规模扩大通过促进产业结构不断优化升级的途径会引起就业人数增加。杜传忠和许冰[14]实证研究了我国的技术进步对就业的影响,得到短期内技术进步阻碍就业规模的扩大,但是长期地产业结构优化升级能够促进就业的结论;二是产业结构与就业的关系方面。例如,徐光平和景建军[15]分析了我国长三角地区及山东省的就业结构与产业结构的相关关系。张文玺[16]、张建华和王慧丽[17]实证研究了我国产业结构与就业结构的偏离程度。于晗[18]认为产业结构和就业结构两者之间是相互调整的演进趋势,并且对两者的变动趋势进行了预测,提出就业结构的发展变化相对要滞后于产业结构的变化。
从以上文献可以看出,大部分国内学者集中研究人力资本结构、产业结构和就业三者之中两者之间的关系,较少地对它们三者之间的互动关系进行系统的研究,即使有,相关文献也大多从高等教育结构角度进行研究,例如,马力和张连城[19]对高等教育结构、产业结构和就业的互动关系进行了研究,认为三者之间存在互动共变关系和时间滞后关系。本文认为我国近年来虽然产业结构不断优化,同时高等教育规模不断扩大,但是呈现出地区差异,尤其是我国东、中、西部三大地区产业结构优化程度和就业人员的受教育程度差异明显。本文通过构建空间面板模型,将在促进就业目标下从三大区域方面研究不同教育层次结构的人力资本与产业结构优化之间的空间联动关系。
二、促进就业目标下人力资本结构与产业结构优化的影响关系分析
在经济发展过程中,产业结构优化升级是核心,人力资本是产业结构优化升级的基础。但是仅是人力资本规模的扩大,并不必然会带来产业结构优化升级,与人力资本的数量相比,人力资本结构与产业结构的匹配更为重要。其中人力资本的教育层次结构与产业结构之间关系随着所处经济增长的阶段不同是有变化的,就业是两者进行匹配的结果,当教育层次结构与产业结构相匹配时,会促进就业。
本文采用国内学者马力和张连城[19]提出的观点,根据产业结构调整不同阶段的驱动要素来源不同,将产业结构调整阶段分为初级阶段和高级阶段。在初级阶段期间,产业结构调整从以第一产业为主转变为以第二产业为主,工业化水平较低,对技术的要求不高,就业需求量较大,人均收入水平普遍较低,导致对教育普遍不被重视,在这一期间人力资本教育层次结构呈现出初等教育和中等教育所占比重最大,高等教育所占比重较小的特征,教育层次结构变化在产业结构调整过程中处于被动地位和从属地位,所以这一阶段教育层次结构与产业结构优化升级的关系表现为根据产业结构的调整变化推动教育层次结构的变化,从而会促进就业增加。在高级阶段期间,经济增长速度减缓,这一阶段为了满足人们日益多样化的需求,产业结构内部不断细化,促进产业结构不断优化升级,即从第二产业为主转变为以第三产业为主,并且在第三产业内部不断分化催生出新的产业,即从劳动密集型产业转变为资本技术密集型产业,这就要求人力资本具备较高的专业化水平,并且更需要创新能力,因此,这一阶段各种类型的人才成为经济增长的主力军,教育作为人才的主要培养途径在经济发展过程中越来越重要,逐渐在产业结构优化过程中起到引导作用。为了满足受产业结构优化未来发展趋势,教育机构主动不断调整其结构,从而教育层次结构的变化具备了主动性。所以这一阶段教育层次结构与产业结构优化升级的关系表现为教育层次结构变化推动产业结构的不断优化升级,从而促进就业。
三、变量、模型和方法
(一)因变量的测算
鉴于在不同目标下,产业结构优化的测度方法是不一样的,本文是在促进就业的目标下对我国30 个省份的产业结构优化指数进行测算。具体计算过程如下。
(1)计算历年各省三次产业的劳动生产率和增加值的增长率,计算公式为

其中:Li分别表示三次产业的就业人数;LP表示劳动力增长率;Yi分别表示三次产业的增加值;YP表示增加值的增长率;i取值为1、2、3,表示第一、第二和第三产业;t表示年份。
(2)计算历年各省三次产业的就业弹性系数(LT),计算公式为

(3)计算历年各省的产业结构优化指数。为了体现促进就业目标下的产业结构优化,计算t年平均就业弹性的产业结构优化指数,计算公式为

其中:TIS表示三次产业所占比重;IS表示产业结构优化指数。
根据计算结果判定产业结构优化效果,如果这一指数值大于1,说明该地区高就业产业的产值比重上升,从而意味着产业结构变化会促进就业,即产业结构趋于优化。计算结果值越大,产业结构优化程度更加显著。反之,表示没有得到优化。在计算结果基础上,计算最近5 年的产业结构优化指数的算术平均数,按(103%,+∞]、(99%,103%]和(0,99%]分为3 类,结果见表1。
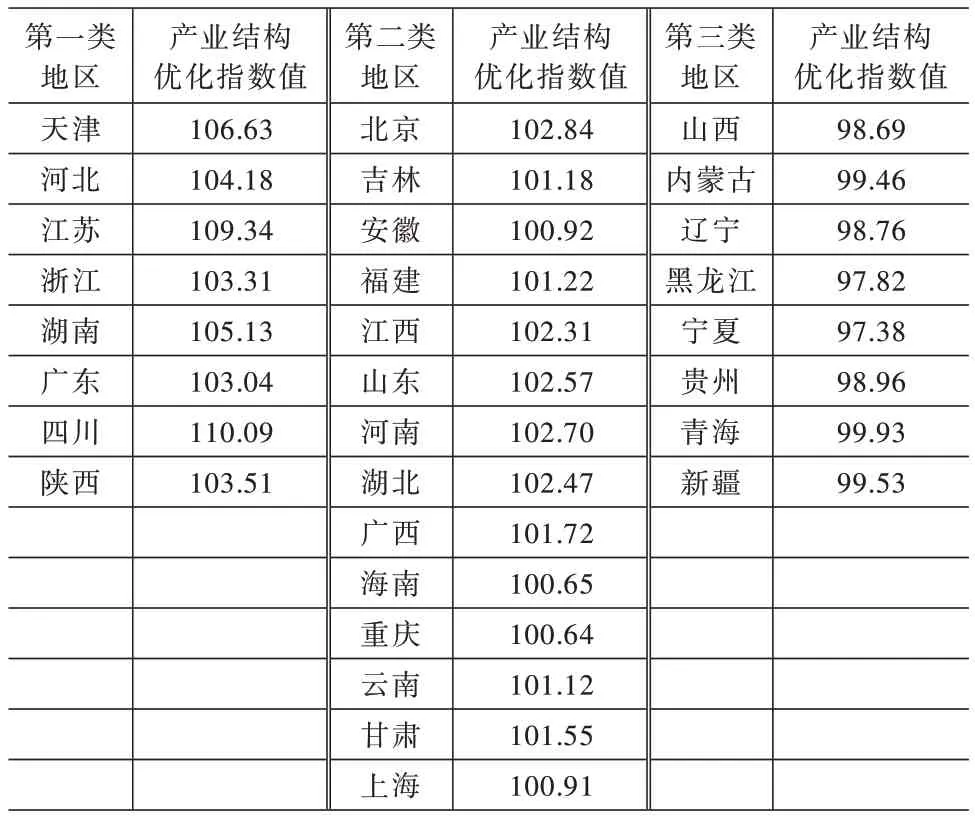
表1 促进就业目标下的产业结构优化指数的区域特征
(二)自变量的选取
本文从供给方面的影响因素角度来考虑,在市场体系中,影响产业结构优化升级的要素包括国内和国外两个部分,国内要素包括劳动力、资本和技术水平,国外要素包括进出口贸易。这些要素的流动性决定了产业体系的产出结构。如果它们不断升级,产业结构随之会不断升级。本文将这些因素的量化指标作为自变量纳入模型中。
(1)不同教育层次的人力资本。本文将人力资本结构按教育层次可分为初等教育、中等教育、高等教育的人力资本,分别用文盲和小学受教育就业人数所占比重(PL)、初中和高中受教育就业人数所占比重(SL)、大学专科、本科及研究生受教育就业人数所占比重(HL)表示初、中、高3 个层次的人力资本。
(2)固定资产投资。固定资产投资是推动产业结构优化升级的直接原因,加大对资本技术密集型产业的固定资产投入,将推动这些产业比其他产业以更快的速度发展,从而推动产业结构优化升级。本文选取全社会固定资产投资额在GDP(国内生产总值)中所占比重代表固定资产投资水平(FI)。
(3)技术水平。技术改革创新是推动产业结构升级的根本动力,技术创新不仅可以促使不断产生新兴产业,同时能促进产业效率的明显提高,并通过带动相关联产业的发展,促使产业结构优化升级。本文选取技术成交额在GDP 中所占比重作为代表性指标(TL)。
(4)进出口贸易。对外贸易是影响产业结构变动的主要外部因素之一,可以通过增加资本积累、促进技术进步、引导消费需求结构变化等途径,对本国产业产生关联和示范等效应,进而促进本国产业结构的优化升级。本文选取进出口额在GDP 中所占比重作为代表性指标(FT)。
(三)数据来源
本文研究样本范围为我国30 个省份(西藏地区和港澳台地区因数据缺少剔除),并将30 个省份分成东、中、西三大地区作为3 个样本进行分析①东部地区是指北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南11 个省级行政区;中部地区指黑龙江、吉林、山西、安徽、江西、河南、湖北、湖南8 个省级行政区;西部地区指四川、重庆、贵州、云南、陕西、甘肃、青海、宁夏、新疆、广西、内蒙古11 个省级行政区。。研究时期为2005—2018 年,相关数据来自于《中国统计年鉴》和2006—2019 年期间30 个省份统计年鉴。
(四)产业结构优化指数的空间自相关检验
本文的产业结构优化指数是在促进就业目标基础上构建的,基于人口与产业在区域之间的流动性,理论上应该存在空间相关性,但是由于采用统计指数法,是否有显著的空间相关性需要论证。因此,本文采用Moran’sI指数法进行检验,结果见表2。由表2 可知,Moran’sI指数均为正且显著,表明全国产业结构优化指数在2005 年以后呈现显著的空间正相关关系,即我国自2005 年起在促进就业目标下产业结构优化在全国范围扩散效应显著。
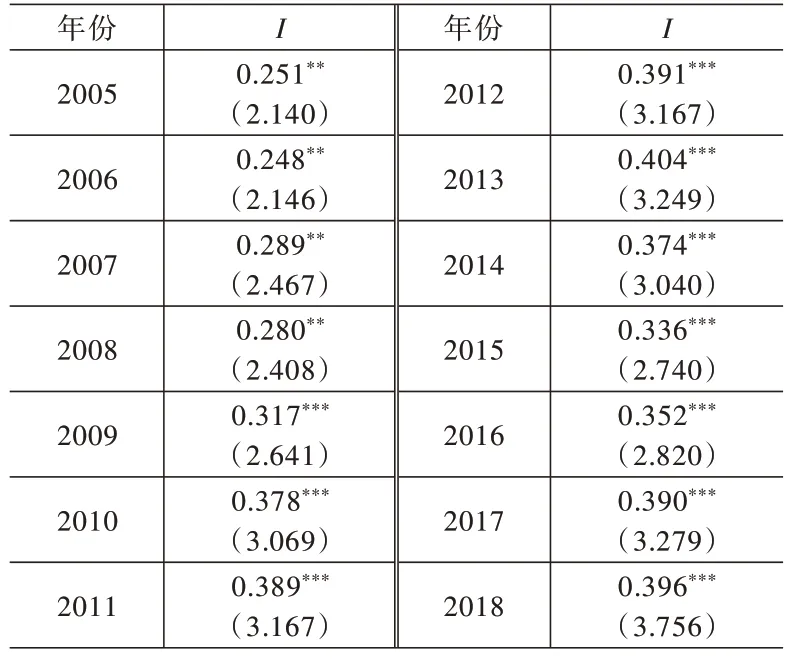
表2 2005—2018 年全国产业结构优化指数的空间自相关检验
(五)空间计量模型的选择与检验
常用空间计量模型包括空间杜宾模型(SDM)、空间滞后模型(SLM)和空间误差模型(SEM)3 种类型。本文拟选择SDM 模型作为用于测度教育层次结构变化对我国产业结构优化升级影响,主要原因是受就业人员、资本、技术等因素流动的影响,一个地区的产业结构优化不仅受到本地区各层次教育水平就业人员的影响,还受到邻近地区不同层次教育水平就业人员的影响;此外,由于示范效应的存在,相邻省份的产业结构优化水平也会影响本地产业结构优化水平,而且SDM 模型包括解释变量和被解释变量的滞后项,模型设定上能够体现本省和邻接省份不同层次教育的人才资本对于产业结构优化的影响,形式如式(4)所示:
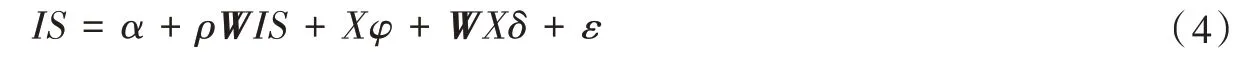
其中:IS表示产业结构优化;α表示常数项;ρ表示被解释变量的空间滞后系数;W表示空间权重矩阵;X表示一系列解释变量;φ表示解释变量的常数回归参数;δ表示解释变量的空间滞后系数;ε表示残差。
根据SDM 模型的表达式可知,若δ=0,则SDM 模型将变成SLM 模型,若δ+ρφ=0,则SDM 模型将变成SEM 模型,可见,与SLM 模型和SEM 模型相比,SDM 模型更具有普适性。
本文使用Anselin[20]提出的研究方法进行检验,首先,建立不包含空间效应的普通面板回归模型,模型如式(5)所示:

其次,对模型(5)采用OLS 方法进行估计,所得的残差进行LM 检验,发现LM 空间滞后和LM 空间误差均存在且显著,表明可以构建空间面板模型。
最后,利用Wald 统计量进行检验,针对模型(4)进行两个假设检验,两个原假设分别是H0:δ=0 和H0:δ+ρφ=0。Wald 统计量(空间滞后)和Wald 统计量(空间误差)均显著,表明拒绝原假设,则说明SDM 模型作为计量模型进行估计是适合的。
(六)模型估计
本文采用模型(4)的SDM 模型作为待估计的空间计量模型,空间权重矩阵采用空间二进制矩阵,即0⁃1矩阵,估计模型采用LeSage[21]提供的MATLAB 软件来进行。估计结果见表3。
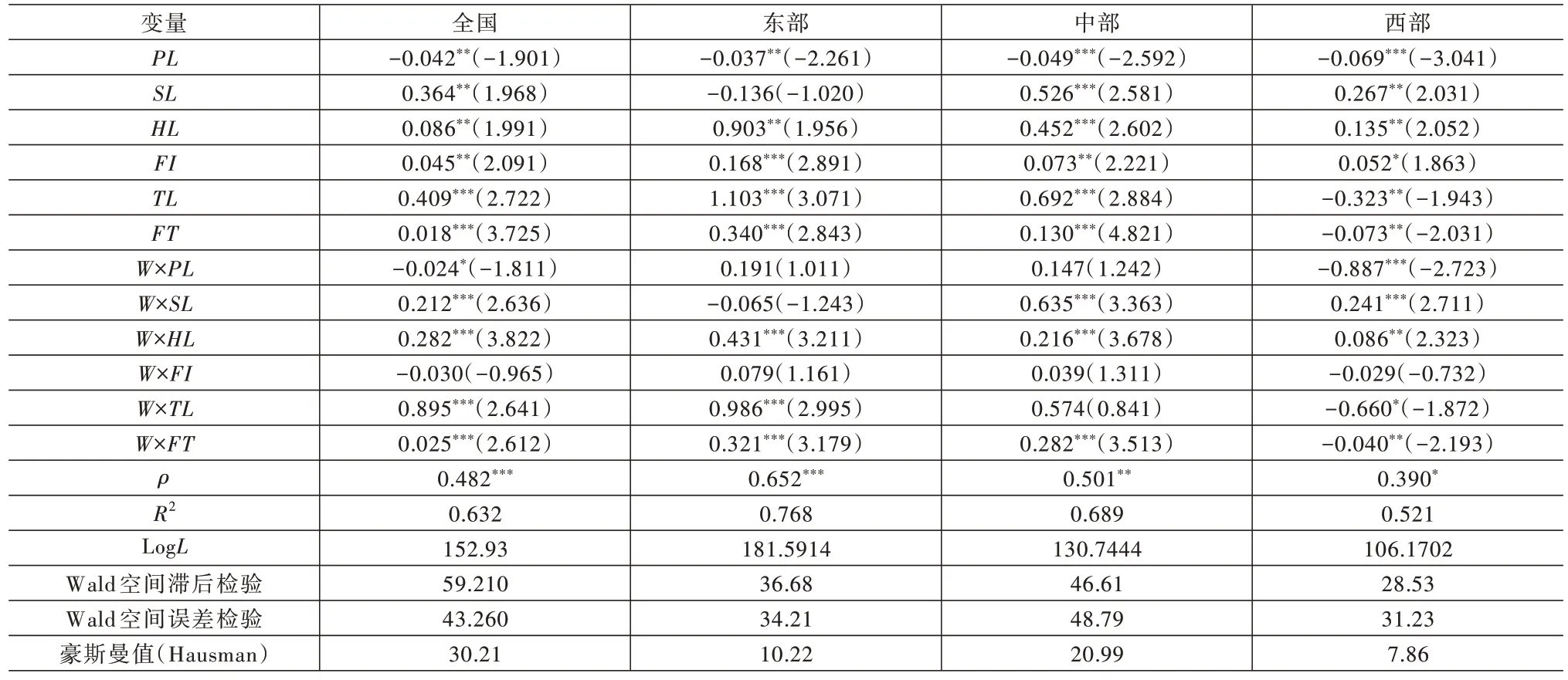
表3 全国与东、中、西部三大区域的SDM 模型的估计结果与检验
(七)直接效应与间接效应的分解
在本文的SDM 模型估计中不但可以通过回归系数来解释自变量对因变量的影响情况,LeSage 和Pace[21]还提出采用偏微分方法测度自变量影响的直接效应与间接效应,模型(4)转换为如下的矩阵形式:
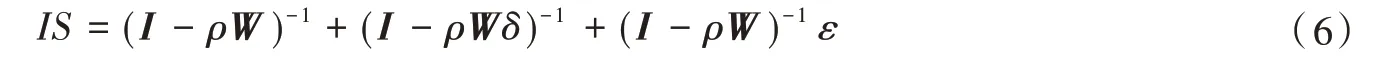
因变量IS中关于第k个变量的偏微分矩阵为
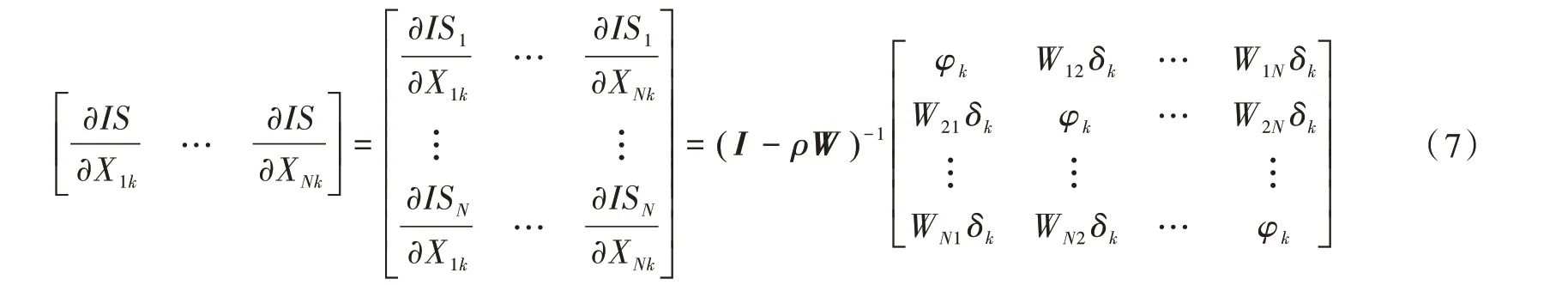
其中:矩阵对角线元素的平均值表示直接效应,表示所有省份各个层次教育就业人数变化引起本地区产业结构优化指数变化总和的均值;矩阵右端非对角线外其他元素的平均值表示空间溢出效应,表示所有省份各层次教育就业人数变化所引起的邻接地区产业结构优化指数变化总和的均值。结果见表4。

表4 基于我国三大地区SDM 模型空间分解的直接效应和间接效应
(八)计算结果分析
通过表3 的ρ可以看到,我国产业结构优化具有显著的空间扩散效应,并且我国东、中、西部三大地区产业结构优化扩散效应呈现出逐渐递减的特点,这种扩散效应强度恰好与我国东、中、西部三大地区的产业承接转移层次相对应。
在初等教育层次的人力资本方面,其变化对产业结构优化升级的直接影响均为负,在2005—2018 年期间我国三大地区初等教育就业人数所占比重呈现下降趋势,表明该变化促进我国产业结构优化升级,其中西部地区的直接影响最为显著。从间接效应来看,我国东部和中部地区空间溢出效应均不显著,西部地区空间溢出效应为负且显著,表明我国西部地区初等教育就业人数比重下降,会促进该地区更多就业人数选择技术性较高层次的产业,对本区域产业结构优化起到推动作用,从而也推动了相邻地区的产业结构优化。
在中等教育层次的人力资本方面,其变化对全国及东、中、西部三大地区产业结构优化升级的直接影响有差异,东部地区的影响为负且不显著,中西部地区的影响为正且显著,其中中部地区的影响最为显著,表明2005—2018 年期间东部地区的经济发展水平对这类层次人力资本的需求已饱和,导致中等层次的就业人数变化对于东部地区的产业结构优化影响不显著,而中部和西部地区的产业结构优化为中等层次的人力资本发挥作用提供发展的空间。从间接效应来看,我国东部地区的空间溢出效应不显著,中部和西部地区的空间溢出效应为正,其中中部地区最为显著,表明2005—2018 年期间我国中等层次教育的人力资本对于中西部地区的产业结构优化升级更为适合,中等层次教育的发展能够带动本区域和相邻地区的产业结构优化升级。
在高等教育层次的人力资本方面,其变化对全国及东、中、西三大地区的产业结构优化升级的直接影响为正,并呈现出递减趋势,表明2005—2018 年期间我国三大地区高等教育就业人数所占比重上升对我国各地区产业结构优化均起到正面促进作用。从间接效应来看,我国东、中、西部三大地区的间接效应均为正,其中东部地区空间溢出效应最显著,西部地区的空间溢出效应最小,表明我国东部地区各省份经济发展水平高,产业结构层次高,对高等教育的人力资本具有很强的吸纳能力,使得邻近省份的优秀高层次人才与不断流向本省,从而显著促进本省的产业结构优化升级;而西部地区大部分省份经济发展落后,产业结构层次较低,导致大部分优秀的高层次人才不断流向东部省份,因此这对西部产业结构优化升级的影响效应较小。
模型其他控制变量对产业结构优化升级的影响方面,在不同地区间出现明显差异。具体来说,固定资产投资(FI)在三大地区的直接效应较为显著,而间接效应不显著。这是由于2005—2018 年期间我国各地区的固定资产投资主要倾向于第二和第三产业中的技术水平高的产业,在一定程度上本省份会吸纳更多人才,从而促进了本地区产业结构优化。技术水平(TL)在东部地区的直接效应和间接效应为正且显著,中部地区的直接效应为正且显著,西部地区为负且显著,表明只有东部地区技术水平真正推动了本地区产业结构优化,并且对邻近省份产生技术外溢。而进出口贸易(FT)对东部地区和中部地区的直接效应和间接效应具有显著的正向促进作用,但对西部地区则为负向作用。
四、政策建议
通过实证分析结果可知,不同层次教育在东、中、西部三大地区效应有较大差异,主要是因为东、中、西部三大地区固定资产投资效果、技术水平、对外贸易等方面的差异,使得不同教育层次的就业人员在各地区的产业结构优化升级中发挥的作用不尽相同,本文从初等教育、中等教育和高等教育3 个层次如何更好地发挥教育对产业结构优化的作用,提出如下建议:
第一,就初等教育层次的人力资本而言,我国东、中、西部三大地区初等教育就业人数比重的变化对产业结构优化升级的直接影响和间接影响在我国西部地区最为显著,表明我国迫切需要加大初等教育资源的投入,尤其是西部地区的教育投入,重点加强西部地区基础教育投入,提高义务教育的质量,让尽可能多的接受初等教育的学生进入到中等乃至高等教育阶段。
第二,就中等教育层次的人力资本而言,通过前文的实证分析可知我国三大地区中等教育就业人数比重的上升对中西部地区产业结构优化的直接影响和间接影响效应为正,表明目前我国中西部地区对中等教育的人力资本仍有较强的吸纳能力,所以中西部地区要重点加大中等教育投入,通过继续教育、培训等方式提高中等教育就业人员的质量,进而增强中等教育的人力资本对本地区产业结构优化升级的影响力度;其次,促进中西部地区的中等教育在区域间分布结构合理化,让社会各阶层人群和低收入群体更多地进入到中等教育阶段。
第三,就高等教育层次的人力资本而言,通过前面的实证分析可知我国东部地区高等教育的就业人数对产业结构优化影响的直接效应和间接效应最为显著,但在中西部地区的影响还是偏小。但是未来我国产业转移的进展将会不断由东向西的推进,中西部地区将对高等教育需求不断上升,因此,一方面我国东部地区高等院校进一步要加强专业结构调整;另一方面我国东部地区高等院校要发挥好向中西部的扩散效应,加强与中西部地区高等院校的合作,帮助中西部地区重点培养代表本地区未来产业结构优化调整趋势所需的特色专业。此外,我国中西部地区的高校毕业生选择去东部发达地区就业的比率偏高,存在“孔雀东南飞”的现象,因此,我国中西部地区的政府需要做好财政支持和人才供求等信息引导工作,加大本地区所需人才的各方面待遇投入,创造各种的条件让本地区需要的相关专业的优秀毕业生尽量选择在本地区就业工作,并且能够发挥出他们的专业特长。
