区域配电网全寿命周期成本优化研究
2020-11-20刘志伟董力通谷志红齐慧文陈英华葛艳琴
刘志伟,董力通,谷志红,齐慧文,陈英华,葛艳琴
(1.国家电网山西省电力公司经济技术研究院,太原 030000;2.国家电网经济技术研究有限公司,北京 102209)
随着新一轮电力市场化的有序推进,电网企业在提高设备可用率和供电服务质量的同时,要减少运行成本,提高企业效益[1]。配电网作为连接输电系统与用户的重要纽带设备数量多、元件分布广、运行方式复杂,其成本随区域不同呈现出明显差别,不同区域的自然条件、经济条件、技术发展程度多样化组合增大了成本管控的难度,现阶段亟需掌握配电网的成本变动规律、准确定位最有效的成本增量控制方向,从而降低配电成本优化配电网投资策略。
许多学者针对配电网系统进行了相关研究。刘自发等[2]建立了微电网的成本效益模型和配电网的综合效益模型,对各项成本效益做出量化评估后针对配电网建立了最优效益模型。韩俊等[3]提出一种基于停电损失计算与成本分析的配电网单元制供电网格可靠性规划方法,分析了停电损失、投资成本与可靠性指标间的关系。全寿命周期理论能够从时间维度横向梳理掌握成本发生情况。Politano 和Frohlich[4]将电网费用成本发生参数与目标函数联系起来进行优化求解。刘波[5]侧重于全寿命周期成本管理的重要阶段进行探讨。李英和孙素苗[6]基于输配电价改革背景,对现行的输配电成本核算现状进行了分析。Morea 等[7]分析变压器负载情况与全寿命成本的关系,给出不同负载率情况下全寿命周期成本的变化趋势。Julia 和Lina[8]提出光伏风电混合式发电系统的全寿命周期成本的计算模型及经济评估方法。李咸善等[9]提出了一种基于灵敏度分析的微电网全生命周期多目标优化模型,基于拟合法求出优化目标对这些关键因素的灵敏度获得微电网全生命周期适应性优化配置方案。崔馨慧等[10]将关键因素灵敏性分析改进、优化应用于电网稳定裕度计算、电网规划方案优化、输电线率线损率降低等问题。张彦和刘金森[11]对贵州输电电网理论线损率的影响因素进行了灵敏度分析。李涛等[12]建立了计及全寿命成本和收益的微电网储能优化配置模型,进一步证明了在安全范围内,通过套利的经济手段降低了其成本。鲁改凤等[13]建立了全寿命周期成本和收益的模型,采用内外层所采用的遗传与模拟退火相结合的算法提出降低成本优化配置策略。王永利等[14]从风机无功成本、安全能效成本、改进挣值法几个方面对电力系统安全稳定性及全寿命周期成本优化问题进行了研究。宋春丽等[15]基于大电网差异化特性,提出了一套差异化全寿命周期成本效益经济评估体系。祝锦舟等[16]基于现行的电网规划方案比选SEC 评价方法,借助全寿命周期理论,提出了一种新的确定电网全寿命周期评估年限的方法。苏卫华等[17]着重考虑电网规划的可靠性成本,提出了一种针对居民用户的需求侧单位缺电成本的求解方法。郑重等[18]基于变压器全寿命周期成本采用威布尔分布的故障概率模型优化运维策略,建立寿命效率指数模型用杜鹃算法进行参数寻优。上述研究极大地推动了配电网全寿命周期成本的研究,但鲜有从区域差异导致电网成本变动原因的角度而寻求成本优化途径的研究。
本文基于系统动力学模型分析了配电网的复杂成本构成,筛选影响成本的关键因子,基于改进蒙特卡法针对关键影响因子构建综合灵敏度模型并计算各关键影响因子对配电网全寿命周期成本影响的综合灵敏度系数,最后以关键影响因子对配电网全寿命周期成本总影响量最小为目标构建成本优化模型,采用GAACS组合算法进行求解。
一、配电网全寿命周期成本灵敏度分析
(一)配电网全寿命周期成本存量流量关系
区域配电网的投资建设、运行维护每年都需要投资大笔的资金,对区域配电网的成本进行梳理能够有效识别配电网成本中的关键因素,为有效管控配电网资产成本提供方向和建议。本节沿着区域配电网全寿命周期的各环节,将期间产生的成本分为4 个环节,分别为初始投资成本、运维检修成本、故障损失成本、退役处置成本,每项成本中又有成本项目多、分支复杂的特点,息费、税金等因素对多条成本产生影响,系统动力学可以剖析全寿命周期成本的复杂构成,梳理4 个环节的成本,构建全寿命周期成本核算模型,如图1 所示。
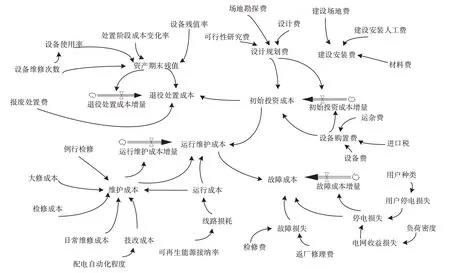
图1 配电网成本系统动力学模型
由图1 可知,用存量流量图来表示区域配电网资产成本和各个因素之间的动态演化关系,该模型中有4个存量变量,分别是初始投资成本、运行维护成本、故障成本和退役处置成本,由于不同配电网区域的经济环境不同、行业发展与新能源电量的接入量不同,存量变量会相应产生流量变量,分别是投资成本增量、运维成本增量、故障成本增量和退役处置成本增量,这4 个流量变量可以为负。
(1)初始投资成本主要部分为设计规划费、设备购置费,建筑安装工程费,其中设计规划费和设备购置费会由于区域不同产生较大区别,根据系数的不同体现区域差异化。设计规划费主要包括可行性研究费、设计费;建安费主要包括直接费、间接费、承包方合理利润与税金;设备购置费主要有设备费和各运杂费组成。

其中:CI表示初始投资成本;Cds表示设计规划费;Cep表示设备购置费;Cei表示建筑安装工程费。
(2)运维成本主要由运行成本、维护成本和其他费用组成。运行成本主要考虑线路损耗;维护成本包括日常维修费、例行检修费、大修费用、技改费用,均受到线损率的影响。
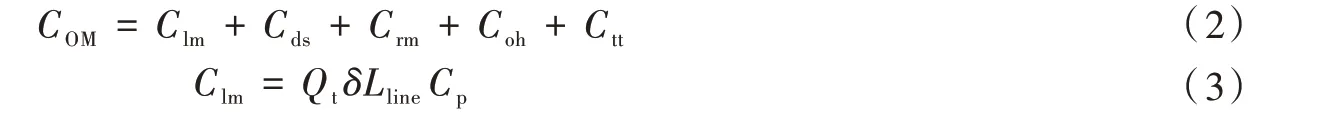

其中:COM表示运维成本;Clm表示运行损耗;Cds表示日常维修费;Crm表示检修费;Coh表示大修费;Ctt表示技改费;Qt表示输电量;δ表示线损率;Ql表示线损电量;Qs表示供电量;Lline表示线路长度;Cp表示网损电价。
(3)故障成本主要包括停电损失成本、故障损失成本。故障损失成本主要包含检修费、返厂修理费,停电损失成本包括电网收益损失、用户补偿损失。

其中:CF表示故障成本;Cfc表示查找故障的成本;Crp表示返厂修理成本;Cil表示电网失电收益损失;Cul表示用户补偿损失;Ql表示总停电量;t表示单次故障停电时间;γ表示停电补偿系数,与用户类型相关。
(4)退役处置成本主要包括设备处置成本和设备净残值,影响因素为固定资产原值、维修率、设备使用率,退役处置成本计算如下:

其中:CD表示退役处置成本;Cdw表示处置所要支付的费用;Fr表示设备原值;φ表示残值率;φr表示默认残值率;a表示设备使用率;b表示设备维修率;Inφr和分别表示残值率和设备使用率与设备维修率比值的函数。
由存量流量图(图1)可知,影响配电网初始投资成本增量的关键影响因子有设备购置费、规划设计费。影响运维成本的关键因子有线损率、技改成本、大修与检修成本;影响故障成本的关键因子是停电损失,影响退役处置成本的关键因子是残值率。
(二)配电网全寿命周期成本灵敏度分析
对上述关键影响因子构建基于蒙特卡洛灵敏度模型,进行灵敏度分析,计算各关键影响因子对配电网全寿命周期成本影响的综合灵敏度系数。但由于传统的蒙特卡洛方法抽取的样本数目多,模拟工作量大,不适合复杂的结构体系,由此结合混合神经网络改进传统蒙特卡洛方法,解决其工作量大的问题。
1.混合网络随机抽样
将所有样本分成n个相互独立的子空间,进行独立的等概率抽样,避免子空间内的重复抽样。假设关键影响因子的概率分布函数为F(wj),由此在n个子空间中产生的边界点有n+1 个,如式(10),为第m个样本在n空间的概率分布,为对于的概率分布函数。
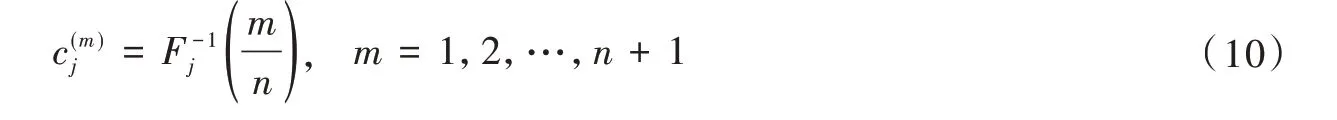
为在独立等概率的子空间随机抽取某样本的计算公式表达,即
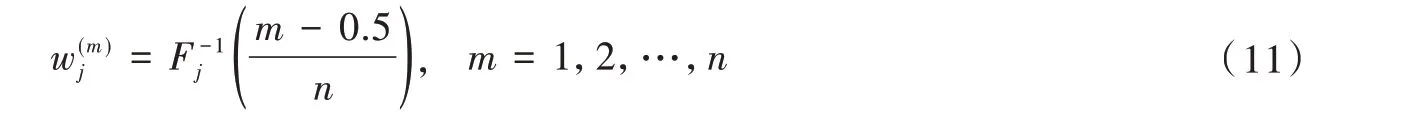
2.计算综合灵敏度系数
基于各关键因子的概率密度函数进行随机抽样,然后根据关键因子的变化范围计算配电网全寿命周期成本的变化情况。为了确定各关键因子对配电网全寿命周期的灵敏度,采取Pearson 相关系数度量关键影响因子与全寿命周期成本间的相关关系,同时引入关键因子的变异系数计算综合灵敏度系数,消除测量尺度与量纲的影响。具体如式(12)所示:
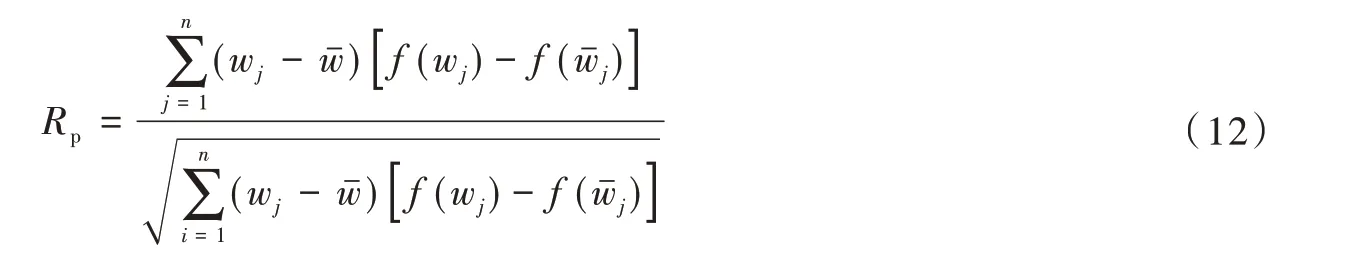

其中:wj表示关键影响因子i;f(wj)表示输入wj下的配电网全寿命周期成本;v表示蒙特卡洛随机抽样次数;Qp表示综合灵敏度系数,系数绝对值越大,说明关键影响因子对配电网全寿命周期影响程度越大,反之亦然,系数正负为关键影响因子与配电网全寿命周期的相关程度,系数为正,代表正相关,反之亦然;ηp表示蒙特卡洛随机抽取下的关键影响因子样本点的变异系数。
二、基于综合灵敏度系数的配电网全寿命周期成本优化模型
(一)目标函数
满足了区域供电需求、保持供电可靠性等约束条件下,实现配电网全寿命周期成本最小,具体配电网目标函数,即

(二)约束条件
结合配电网全寿命周期成本特点,在初始投资、运行维护、停电故障、退役处置4 个阶段基础上,具体约束条件如下。
(1)初始投资约束。配电网在初始投资阶段受到投资额与配电区域电力需求量两方面的约束,式(15)为初始投资成本不能超过总的投资额,式(16)为所建配电网能够满足该区域电力需求,即电力供给量大于等于电力需求量,即

其中:CTotal表示初始投资阶段总的投资额;Qs表示区域的电力供给量;D表示区域的电力需求量。
(2)运行维护约束。运行维护阶段收到线损率及其输电量约束,式(17)为保证配电网输电稳定性,约束线损率的取值范围;式(18)为供电量与输电量及其损耗量之间的平衡。

其中:δmax表示线损率允许达到的最大值。
(3)停电与故障约束。为了保障配电网给用户的供电质量,受到停电时间上限及其停电补偿的约束,具体如式(19)、式(20)所示:

其中:γmax、tmax分别表示停电补偿与单词停电故障时间的最大值。
(4)退役与处置阶段约束。退役与处置阶段受到残值率、设备维修率、设备使用率的约束,具体如式(21)~式(23)所示:

其中:φmax表示残值率的上限;bmax表示设备维修率的上限;amax表示设备使用率的上限。
三、模型计算与求解
(一)GAACS 组合算法
遗传算法具有全局搜索的优势,但忽略反馈信息导致求解速度受到影响;蚁群算法则基于信息素搜索最优解,但信息素的缺乏会降低算法的效率。将两种算法进行组合,利用遗传算法的全局搜索优势为蚁群算法提供信息素进行最优解的搜寻,由此提高优化效率,减少搜寻时间。
(1)始化种群。个体数量也即关键因子个数确定种群规模,并与关键因子取值一一对应。假定关键因子wj的编码为wj=[wj1,wj2,…,wji,…,wjn],其中wji表示第j个关键因子的第i个取值。关键因子的取值在其取值范围内随机生成,防止取值超过关键因子的取值上限。
(2)确定遗传算子。算子的选择能够提高算法的计算效率与收敛性,同时变异与交叉算子的有效结合能够保证遗传算法的有效性。由此采取轮盘赌进行采样,进行基因单点的交叉与随机位的变异,并引入精英保留策略,即子代中适应度低的个体被父代中较优个体替代。
(3)转入蚁群算法的时间点。首先假设遗传算法的最大最小迭代次数与子代的最小进化率。通过比较每一代的进化率与设定的最小进化率,假如连续n代的子代进化率小于最小进化率,则从遗传算法进入到蚁群算法。
(4)更新蚁群转移概率。蚂蚁a在搜索过程中的转移概率如式(24)所示:
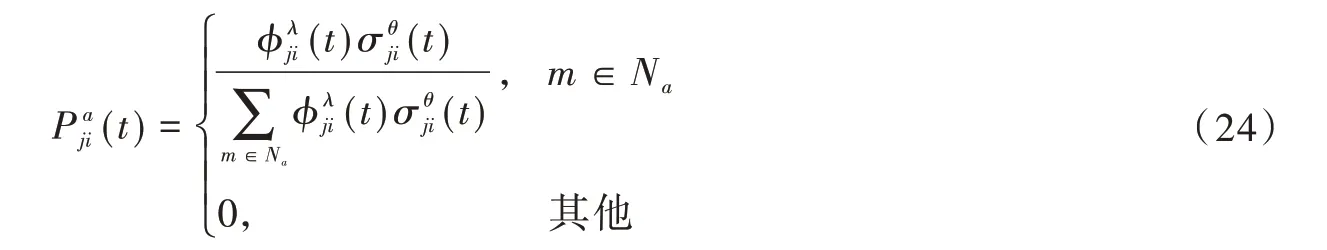
其中:(t)表示t时刻支路i上相应的信息素;(t)表示蚂蚁在t时刻的能见度;λ表示信息因子;θ表示期望启发因子。后面蚂蚁的行进方式与信息素受到前面蚂蚁行走方式的影响,所以需要在前面蚂蚁行进一步之后进行信息素的更新,即
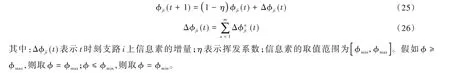
(二)模型具体求解流程
基于GAACS 组合算法的模型求解流程具体如图2 所示。
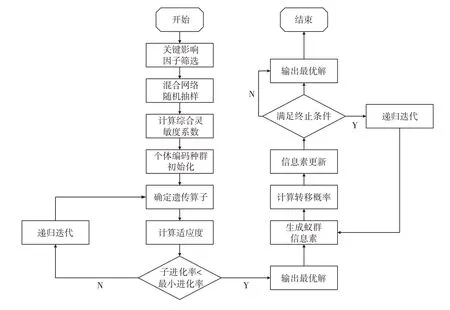
图2 模型求解流程图
(1)筛选关键因子,计算综合灵敏度系数。通过筛选影响配电网全寿命周期成本的关键因子,利用改进的蒙特卡洛方法进行随机抽样,由此计算不同关键因子的综合灵敏度系数。
(2)初始化种群,确定遗传算子。根据关键因子数目确定种群规模,对关键因子的取值进行编码,初始化种群,通过轮盘赌采样方式确定遗传算子。
(3)计算适应度,判断转入蚁群算法的时间点。通过比较子进化率与最小进化率的大小,判断是否转入蚁群算法,当连续n代的子进化率<最小进化率,则转入蚁群算法,反之,则继续递归迭代。
(4)形成蚁群信息素,计算转移概率。通过式(24)计算蚁群行进的转移概率。
(5)更新蚁群信息素。通过式(25)、式(26)计算蚁群信息素的更新情况。
(6)判断是否达到最优解。通过判断在满足约束条件的情况下,实现了全寿命周期成本最小,若满足,则输出最优解,也即全寿命周期成本最小;若不满足则继续进行递归迭代。
四、算例分析
(一)基础数据
选取某省10 千伏配电网区域共4 个低压台区2017 年的投资建设及运维数据,该配电区域10 千伏主线15 年间最大负荷为2439 千瓦,具体参数见表1。
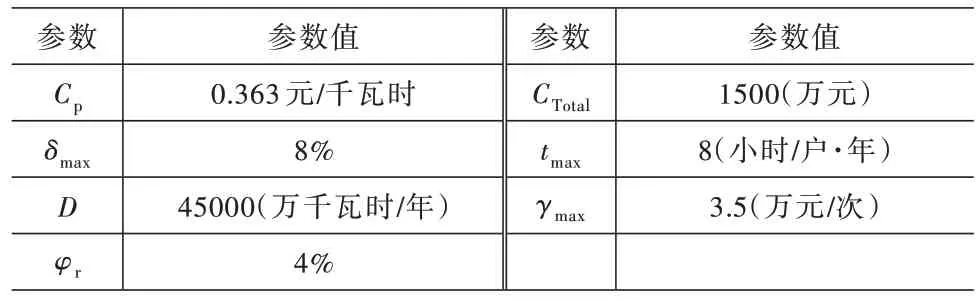
表1 数据参数表
考虑到不同区域间配电网网架结构、供用电情况复杂多变,运维数据不易得,控制变量困难等因素。现依据算例区域配电网基础数据进行模拟,分别考虑自然条件、经济发达程度、技术成熟程度对全寿命周期各项成本的综合影响,模拟出不同情景的区域配电网成本数据,分析全寿命周期成本中各关键因子的综合灵敏度系数,再进一步进行区域配电网间成本的横向对比分析。根据原始数据计算得出各个关键因子的综合敏感系数见表2。

表2 基础综合灵敏系数表
(二)结果分析
1.综合灵敏性度系数
(1)自然条件。不同区域配电网自然条件的复杂性会综合影响成本,地形复杂区域的规划设计难度增加,直接导致规划设计费增高、建安费增加,间接增大运维检修成本;气候潮湿或者极度干燥直接导致初始设备购置费增大;极端天气概率频发导致大修次数增加;综合考虑地形、气候、极端天气发生概率,将自然条件按照利好电网建设运维程度分为4 个等级,依据模拟数据计算得各关键因子的综合灵敏度系数变动如图3所示。
由图3 中变化明显的系数分析可知,自然条件发生变化时,各关键因子的综合灵敏度系数产生变化,其中较为典型的6 个关键因子,分别是设备购置费、大修费、电网损失费、技改费、检修费、用户补偿损失费。当自然条件逐渐利好时,设备购买费和技改费对总成本的影响程度逐渐升高,大修费和检修费对成本的影响程度呈下降趋势,电网损失和用户损失对成本的影响程度变化平滑。分析可知,当自然条件有利于配电网建设运维时,初始建设投资和技改性投资应是关注的重点,尤其是设备购置环节,综合灵敏系数最高为0.95;运维检修的改进优化对成本的优化作用随环境条件变好而减小;电网损失和用户补偿损失与没有环境变化呈现明显的线性关系。
(2)经济条件。区域经济发达程度的差异带来区域负荷密度变化,线路、设备的初始投资成本随之变化,负荷密度高时,区域配电网的网损、线损率、设备利用率均会升高,大修、检修频率增加,成本相应增加。区域用户特性会对用户补偿损失、年运行小时数等产生影响,对故障停电时间、带电作业能力提出不同要求,结合经济条件变化的区域成本数据,各因子的综合灵敏度系数变化如图4 所示。
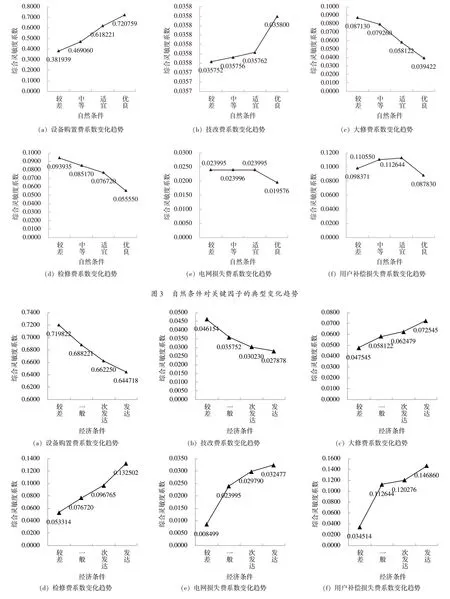
图4 经济发达程度变化时关键因子的典型变化趋势
由图4 中变化明显的系数分析可知,随着经济逐渐发达,区域配电网的设备购买费和技改费的综合灵敏度系数呈下降趋势,大修费、检修费、电网损失用户损失呈上升趋势。设备购置环节和技改环节会随着区域经济的发达对成本的影响逐渐降低,技改费的影响变动幅度较大;而运维检修环节的成本会随经济的发达对总成本的影响逐渐增大,尤其是检修环节,分析可能由于区域负荷密度大,增加了检修次数和检修成本;而电网损失和用户补偿损失的影响也明显升高,验证了负荷密度大的区域供电保障、电网可靠性的会越发重要。
(3)技术条件。区域配电网的技术成熟度也会影响全寿命周期的各个环节的成本,技术成熟程度可以从供电可靠性、配电自动化程度以及可再生能源接入量3 个角度出发,供电可靠性高的区域故障发生概率低,电网损失和用户补偿损失低,初始投资成本及技改费较高;配电自动化程度高的区域则运维检修的成本低;可再生能源接入量大的区域技改费高,网损率、线损率高,具体变化如图5 所示。

图5 技术成熟程度变化时关键因子的典型变化趋势
由图5 中变化明显的系数分析可知,随着技术成熟程度增加,设备购置费综合灵敏度系数的升高,其对成本的影响程度增大,表示技术要求越高,设备购买环节存在越大的成本控制潜力;大修费、电网损失费、用户损失的综合灵敏度都明显下降,表明区域技术程度越成熟,运维检修以及故障损失对成本的影响在减少,那么对这几项成本的优化研究可以适度降低;值得关注的是技改费的综合灵敏度出现凹陷,分析推断技术程度较差区域可能因为智能化电网建设进行技改,而技术发达区域会因为新能源项目进行技改。
2.成本优化结果
为研究区域条件综合时各关键因子对成本的综合影响,简化自然、技术、经济的影响程度,分为优、中、差3 个等级,共有27 种情景组合方式,现针对典型情景进行成本优化分析,由于情景组合数量较多,按照自然条件优、中、差将结果分为3 个板块进行分析,见表3 和图6。

表3 情景1~情景9 条件等级情况

图6 情景1~情景9 的综合灵敏度系数变化曲线
情景1 曲线和情景9 曲线对比分析设备购置费的综合灵敏度因数明显下降,下降幅度在0.25 左右,表明技术条件、经济条件差时设备购置费对总成本的影响变小;用户损失的综合灵敏度系数略有上升,幅度在0.04 左右,表明经济、技术条件变差时用户补偿损失对总成本的影响变大。情景1 曲线与情景7 曲线分析仅经济条件改变,设备购置费下降约0.15,情景1 曲线与情景3 曲线对比可看出,设备购买费的综合灵敏度系数下降0.1 左右,比经济条件变化时影响变动小,证明技术条件的度区域成本影响力度小于经济条件,见表4和图7。

表4 情景10~情景18 条件等级情况
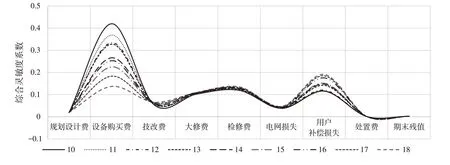
图7 情景10~情景18 的综合灵敏度系数变化曲线
情景18 曲线与情景9 曲线对比分析可知,自然条件变差时,设备购置费对总成本影响程度下降约0.07,检修费影响程度总体升高,见表5 和图8。
综合情景1~情景27 的综合灵敏度系数曲线可知,对区域配电网全寿命周期成本影响最大的关键因子时设备购置费在0.3 上下浮动,其次是用户损失在0.2 上下浮动、检修费在0.12 上下浮动、大修费在0.1 上下浮动,对全寿命周期成本进行优化可从这几项出发能够得到较大的降成本效果;由情景1 曲线和情景27 曲线对比分析,区域条件整体变差时,各影响因子对成本的影响均减弱,设备购置费下降了0.3 左右,用户损失补偿下降了0.08 左右,检修费和大修费的影响基本不变,表明随着大修、检修环节无论在什么区域都有一定降成本能力,其影响力基本不随环境整体变化而变化。情景1 曲线与情景19 曲线分析可知,设备购置费的综合灵敏度系数下降0.11 左右,比经济条件变动的0.15 要小,说明自然条件对区域成本的影响力度也小于经济条件,说明区域经济条件是对区域成本影响最大的条件。
结合27 组情景的关键影响因子的综合灵敏系数对配电网全寿命周期成本影响总量进行优化求解,如图9 所示。

表5 情景19~情景27 条件等级情况
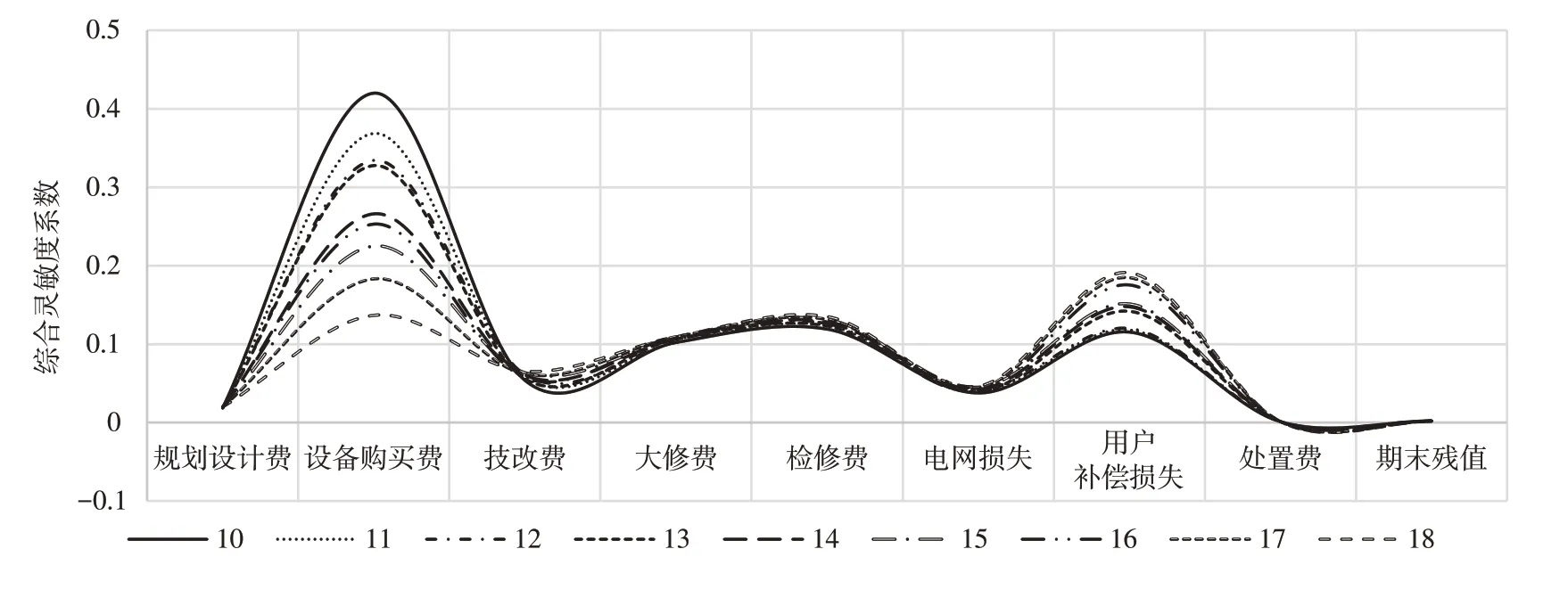
图8 情景18~情景27 的综合灵敏度系数变化曲线
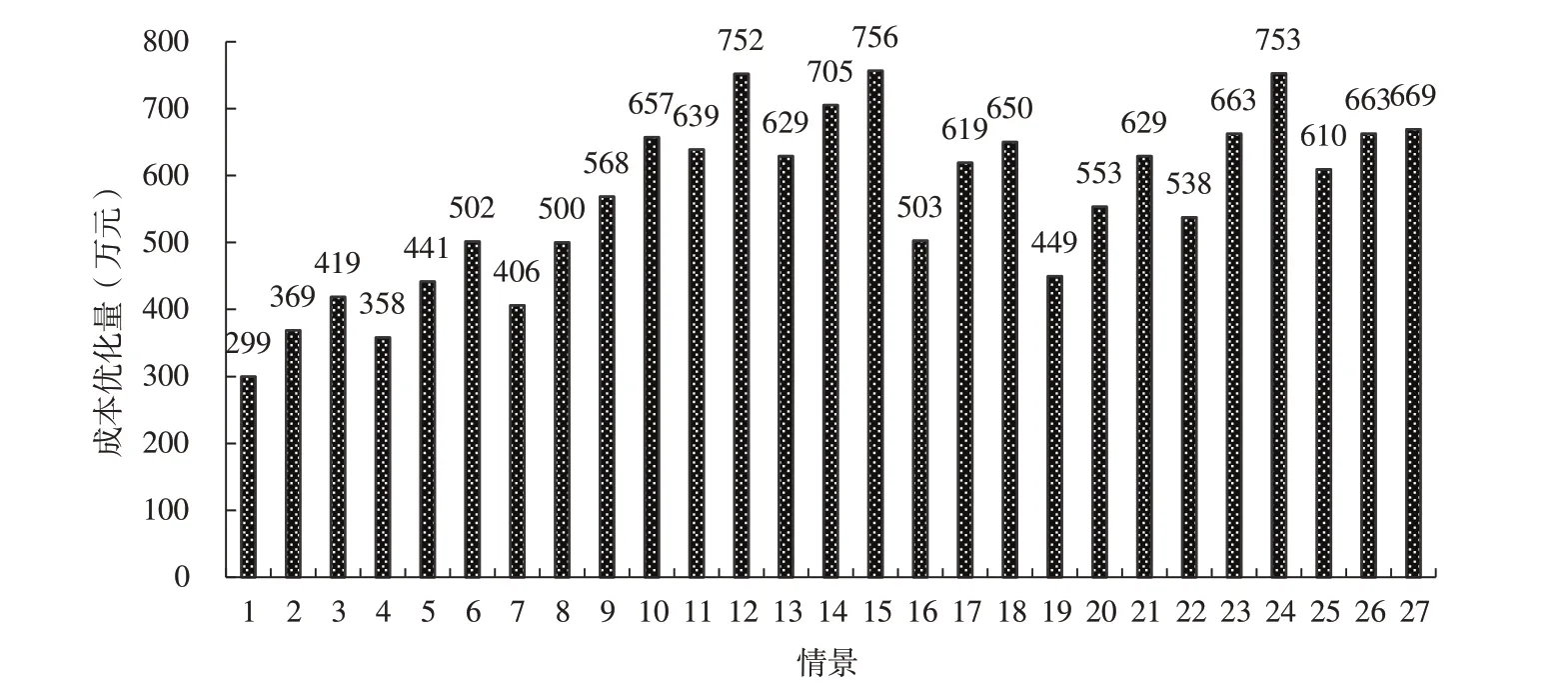
图9 27 种情景下成本优化结果
由图9 可知,关键影响因子对配电网全寿命周期成本总的影响量在299 万~895 万之间,差距较大,证明区域不同配电网成本控制能力有较大区别;影响量最小的是情景1,证明区域总体条件好时,成本优化空间较小,最大是情景15,其次情景24 和情景12,说明当自然、经济情况较好,技术及条件较差时,具有较大的成本优化空间,此种区域进行技改能够有效地降低配电网成本。
五、结论
为了整体分析配电网区域变化对成本优化空间带来的利好条件,本文首先针对区域配电网全寿命周期成本优化问题,从区域配电网自然、经济、技术3 个维度进行了差异性分析,以及识别了关键成本因子和确定了综合灵敏度系数。然后建立了区域配电网全寿命周期成本优化模型和采用了GAACS 组合算法对其求解,具体得到结果如下。
(1)建立了基于系统动力学的配电网全寿命周期成本模型;分析了配电网复杂成本构成,并提出影响区域配电网成本的关键因子。
(2)基于改进蒙特卡洛法建立了配电网全寿命周期成本的灵敏度分析模型,发现设备购置费对配电网成本影响最大,其次是用户补偿损失。
(3)通过综合情景分析发现经济条件对配电网成本影响最大,最后求解模型得出各种情景成本影响总量,发现技术条件差的区域降低成本能力较大。
