浇注型聚氨酯弹性体热老化条件下的本构关系

2020-11-20王培文王敏杰赵书德

弹性体 2020年5期

王培文，王敏杰，段飞，赵书德

(大连理工大学模塑制品教育部工程研究中心，辽宁大连 116024)

浇注型聚氨酯弹性体(CPU)作为聚氨酯的一大分支，具备塑料与橡胶的双重特性，广泛应用于国民经济的各个领域[1]。然而，CPU在贮存和使用过程中，会受到外界环境中热的影响，从而发生热老化，使分子链断裂，微观结构和组成成分发生改变，导致其力学性能大幅下降甚至失效，从而严重影响CPU制品的使用性能和服役性能。本文研究的CPU是某军工产品的主要构成材料，其力学性能会对军工产品的使用性能和服役性能产生直接影响，鉴于该军工产品用途的特殊性，研究其构成材料CPU老化192 h的力学性能最具有代表性。为了对老化192 h的CPU力学性能有全面清晰的认识，需要对其应力-应变关系进行研究，建立超弹性本构模型。

关于超弹性材料的本构关系，国内外学者通过对超弹性材料进行大量研究，构建了多种用于表征超弹性材料力学特性的本构模型[2-7]，然而由于超弹性材料和使用环境的不同，难以用一个统一的本构关系模型对所有超弹性材料的力学性能进行表征，需针对具体材料、具体使用情况进行本构关系的构建。本文通过对老化192 h的CPU进行单轴拉伸实验，得到了CPU的应力-应变关系，采用Mooney-Rivlin模型、Yeoh模型和Neo-Hookean模型对应力-应变曲线拟合，最终基于Mooney-Rivlin模型，建立了老化192 h的与温度相关的超弹性本构模型。

1 实验部分

1.1 原料

PTMG-TDI型预聚体：NCO基质量分数为3.91%，淄博华天橡塑科技有限公司；3,3′-二氯-4,4′-二胺基二苯甲烷(MOCA)：分析纯，苏州湘园精细化工品有限公司。

1.2 仪器及设备

电子天平：JJ2000B，美国双杰有限公司；电动搅拌器：MYP2011-100，上海梅颖浦仪器仪表制造有限公司；电热鼓风干燥箱：DHG-9123A，上海捷呈实验仪器有限公司；微机控制电子万能试验机：CMT-4204，美斯特工业系统(中国)有限公司。

1.3 试样制备

为清晰表述试样制备过程，现将PTMG-TDI型预聚体作为A组分，MOCA作为B组分。

称取适量A组分，加热至85～90 ℃，按扩链系数0.85称取B组分，加热至105～110 ℃，将B组分快速倒入A组分中，搅拌均匀后真空脱泡，然后倒入预热至80～85 ℃的模具中，凝胶10 min后合模，放入90 ℃的电热鼓风干燥箱中熟化16 h，制成1型标准哑铃状试样，试样具体尺寸参照GB/T 528—2009。

1.4 热老化实验

参照GB/T 3512—2014，将试样放置于温度为40 ℃、60 ℃、80 ℃、100 ℃、120 ℃、140 ℃的电热鼓风干燥箱中进行热老化实验，分别在实验进行到192 h时取样测试。

1.5 性能测试与表征

按照GB/T 528—2009，在室温下对试样进行单轴拉伸应力-应变性能测试，拉伸速度为500 mm/min。

2 结果与讨论

2.1 应力-应变关系

CPU在不同温度下老化192 h后的应力-应变关系如图1所示。

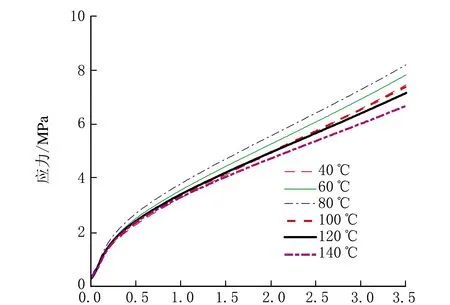
应变/%

从图1可知，当对老化192 h的CPU进行单轴拉伸时，其应力随应变呈现出明显的非线性变化。在拉伸初始阶段，应力值随着应变的增加呈现线性增大趋势，CPU发生弹性变形；随着拉伸过程的进行，曲线发生非线性转变，应力的增大速度有所减缓，CPU发生应变软化，此阶段的曲线斜率明显小于弹性变形阶段；在整个拉伸过程中，CPU的应力-应变曲线没有表现出取向硬化现象。因此，CPU单轴拉伸下的应力-应变曲线为没有取向硬化阶段的凸型曲线。

通过对比不同温度下的应力-应变曲线可以发现，不同温度下的应力-应变曲线的斜率具有明显的差异。当温度低于80 ℃时，随着温度的升高，曲线的斜率逐步增大；当温度高于80 ℃时，随着温度的升高，曲线的斜率逐步减小，说明CPU具有明显的温度敏感性。

2.2 超弹性本构模型

浇注型聚氨酯弹性体作为一种超弹性材料，对其进行超弹性本构模型构建时，通常基于以下两个假设：超弹性材料的体积不可压缩且具有各向同性。超弹性本构模型通过应变能密度函数W进行表示，它由Cauchy-Green变形张量中的三个应变张量不变量I1、I2和I3进行表示，如式(1)所示。

W=W(I1,I2,I3)

(1)

三个应变张量不变量I1、I2、I3可通过主拉伸比λi(i=1,2,3)进行表示，当对超弹性材料进行单轴拉伸时，载荷作用方向上的主拉伸比为λ，不妨令λ1=λ，对于体积不可压缩的各向同性材料，I3=1，可得λ2=λ3=λ-1/2，因此，单轴拉伸时三个不变量应变张量I1、I2和I3与主拉伸比λ之间的关系分别如式(2)～式(4)所示。

(2)

(3)

(4)

主拉伸比λ是材料变形后长度L与材料初始标距长度L0之比，如式(5)所示。

λ=L/L0

(5)

由式(5)可进一步推出主拉伸比λ与应变ε之间的关系，如式(6)所示。

λ=L/L0=(L0+ΔL)/L0=1+ΔL/L0=1+ε

(6)

进行单轴拉伸时，超弹性材料应力σ的计算公式如式(7)所示。

(7)

式中：F为试样拉伸过程中承受的载荷，A0为试样未发生形变时的横截面积，L0为试样的初始标距，W为应变能密度函数，λ为载荷作用方向的主拉伸比。

对于单位体积的超弹性材料，A0L0=1，故式(7)简化后，可得应力σ与应变能密度函数W和主拉伸比λ之间的关系，如式(8)所示。

σ=dW/dλ

(8)

为对CPU的力学特性进行准确描述，本文选用三种常用的超弹性本构模型对实验曲线进行拟合，并对拟合结果进行对比分析，选取拟合精度高的作为CPU的超弹性本构模型，下列公式为三种超弹性本构模型的应变能密度函数和单轴拉伸下的应力-应变关系。

Mooney-Rivlin模型(MR模型)[8-9]的应变能密度函数如式(9)所示。

W=A1(I1-3)+A2(I2-3)

(9)

式中：A1、A2均为参数。将式(2)～式(4)、式(6)、式(8)以及式(9)联立，可得单轴拉伸下的应力-应变关系表达式，如式(10)所示。

Yeoh模型[10]的应变能密度函数如式(11)所示。

式(11)中B1、B2、B3均为参数。将式(2)～式(4)、式(6)、式(8)以及式(11)联立，可得单轴拉伸下的应力-应变关系表达式，如式(12)所示。

σ=2A1[(1+ε)-1/(1+ε)2]+2A2[1-1/(1+ε)3]

(10)

W=B1(I1-3)+B2(I1-3)2+B3(I1-3)3

(11)

σ=2[(1+ε)-1/(1+ε)2]{B1+2B2[(1+ε)2+2/(1+ε)-3]+3B3[(1+ε)2+2/(1+ε)-3]2}

(12)

Neo-Hookean模型(NH模型)[11]的应变能密度函数如式(13)所示。

W=C1(I1-3)

(13)

式中：C1为参数。将式(2)、式(4)、式(6)、式(8)以及式(11)联立，可得单轴拉伸下的应力-应变关系表达式，如式(12)所示。

σ=2C1[(1+ε)-1/(1+ε)2]

(14)

2.3 老化192 h的本构模型

Mooney-Rivlin模型、Yeoh模型和Neo-Hookean模型对老化192 h的应力-应变曲线的拟合结果如图2所示，相关系数R2如表1所示，Mooney-Rivlin模型的拟合参数A1、A2如表2所示。

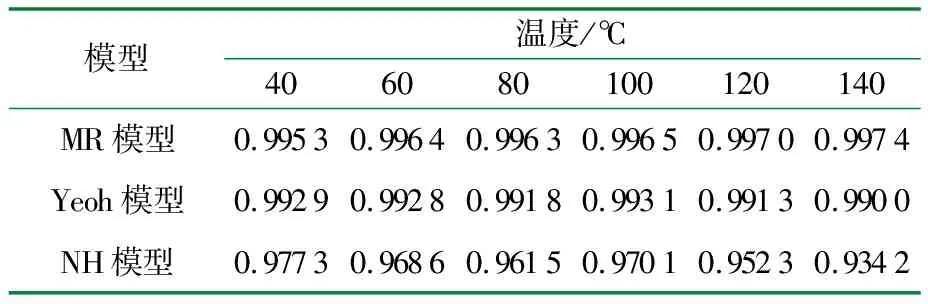
表1 三种模型的相关系数R2

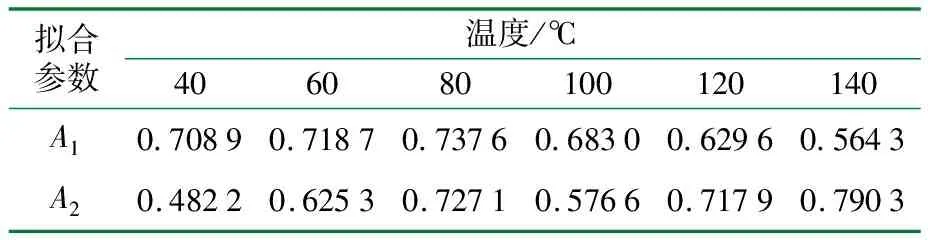
表2 MR模型拟合参数

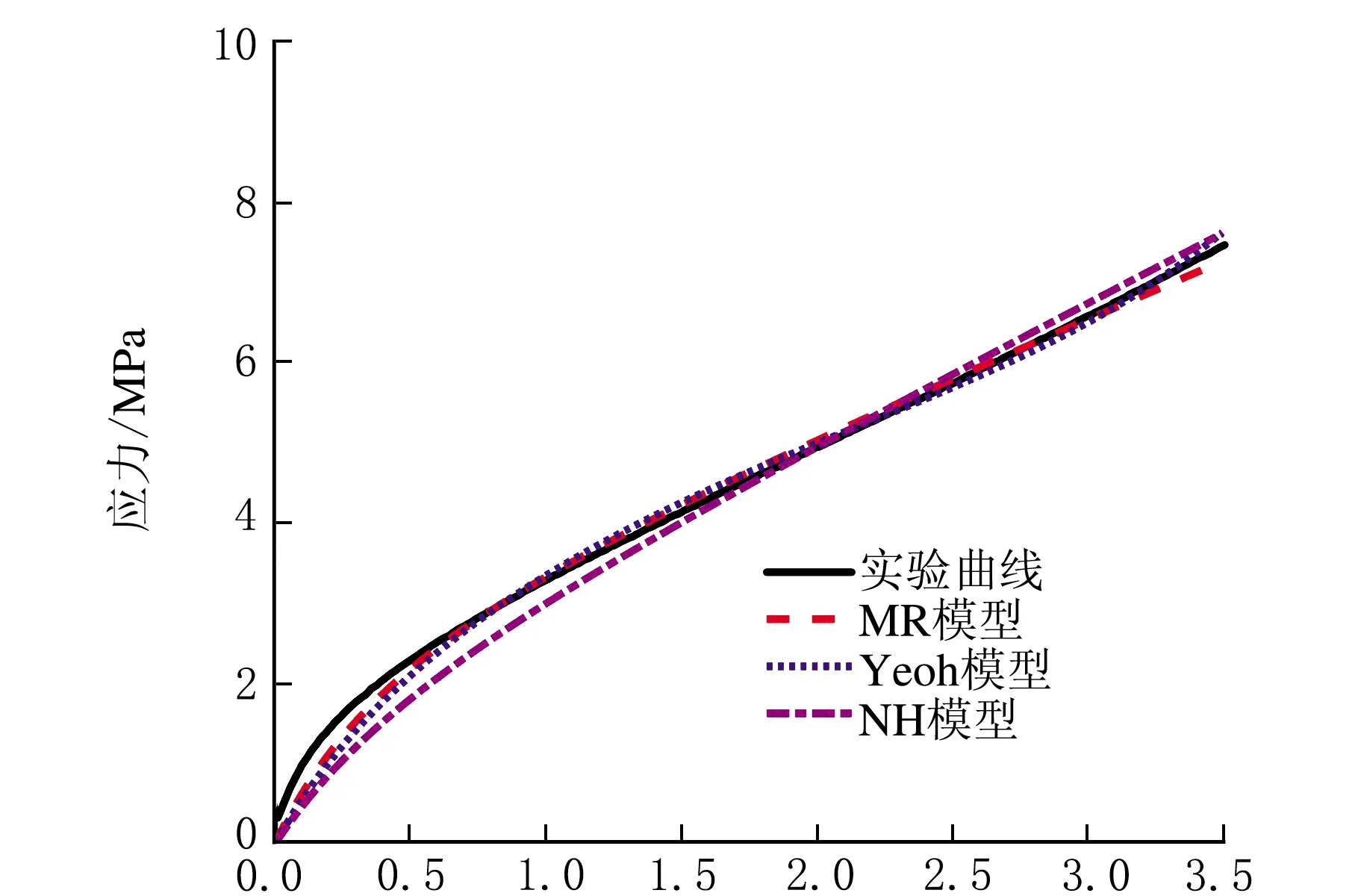
应变/%

从图2可知，Mooney-Rivlin模型的拟合曲线与实验曲线的变化趋势基本相同，两曲线均为没有取向硬化阶段的凸型曲线，且两曲线基本重合；虽然Yeoh模型的拟合曲线与实验曲线具有较高的重合度，但两曲线存在明显差异，Yeoh模型得到的拟合曲线是表现出明显取向硬化现象的S型曲线，与实验曲线的变化趋势不符；Neo-Hookean模型得到的拟合曲线为没有取向硬化阶段的凸型曲线，虽然与实验曲线的变化趋势相同，但与实验曲线的重合度较低，明显偏离实验曲线。

从表1可知，当温度相同时，三种模型得到的相关系数R2由大到小依次排序为：Mooney-Rivlin模型>Yeoh模型>Neo-Hookean模型，说明Mooney-Rivlin模型对实验曲线的拟合精度高于Yeoh模型和Neo-Hookean模型；从数值上看，Mooney-Rivlin模型对CPU在不同温度下老化192 h的实验曲线拟合得到的相关系数R2均超过0.995 3，说明拟合精度较高。

因此，在三种超弹性本构模型中，Mooney-Rivlin模型具有拟合精度高，拟合曲线与实验曲线变化趋势相同的优点，说明该模型能够准确地描述CPU在不同温度下老化192 h的力学特性。

从表2可知，运用Mooney-Rivlin模型对老化192 h的CPU的应力-应变曲线拟合，不同温度条件下得到的拟合参数不同，因此，可以将参数A1、A2视为与温度相关的函数，通过建立参数A1、A2与温度之间的关系，用来表述温度对老化192 h的CPU应力-应变关系的影响。以温度T作为自变量，参数A1、A2作为因变量，采用多项式拟合，参数A1与温度T的拟合曲线如图3(a)所示，关系表达式如式(15)所示，拟合得到的相关系数R2为0.991 2。参数A2与温度T的拟合曲线如图3(b)所示，关系表达式如式(16)所示，拟合得到的相关系数R2为0.935 1。