超密集蜂窝网络智能干扰协调算法

秦爽/QIN Shuang，董星辰/DONG Xingchen，冯钢/FENG Gang

（1.电子科技大学，中国成都611731；2.南京船舶雷达研究所，中国南京211153）

(1.University of Electronic Science and Technology of China,Chengdu 611731,China;2.Nanjing Marine Radar Institute,Nanjing 211153,China)

近年来，随着智能移动终端的快速发展和普及，移动通信业务呈现出了爆炸式增长。有研究发现[1]，在移动通信网中，存在大量的业务热点区域，特别是以住宅、商场、办公楼等为代表的室内热点区域，集中了超过70%的数据业务和50%的语音业务。因此，为了提升热点区域的网络覆盖并增加网络容量，研究者提出了在已有宏基站（MBS）的覆盖范围内，通过部署大量低功耗、低成本的小基站（SBS），形成重叠异构覆盖的超密集蜂窝网络（UDN），来解决移动网络中热点区域弱覆盖的相关问题[2]。

在UDN中，SBS部署密集，站点之间距离很近，一个小基站会同时受到来自MBS和周围其他SBS的干扰。网络中干扰问题十分严重，且干扰环境也很复杂，严重影响了网络用户获得的传输服务质量。因此，如何通过有效的干扰协调，降低网络中不同接入站点之间的干扰，提升网络传输性能是UDN网络需要解决的一个重要问题[3]。

近年来，集中化无线接入网（CRAN）技术作为一种移动接入网的新型组网和部署方式，引起了研究者的广泛关注[4]。在C-RAN网络架构下，移动接入网络由1个中心控制的基带处理单元（BBU）与多个分布式的射频单元（RRH）组成，每个RRH相当于1个SBS。利用C-RAN技术可以方便部署即插即用的SBS，构建UDN，实现对热点区域的密集覆盖[5]。因此，如何在基于C-RAN网络架构的UDN中进行高效的干扰协调，是一个值得深入研究的问题。

干扰协调一直是移动通信网络领域的热点研究问题，而功率控制是实现干扰协调的有效手段。已有很多研究[6-7]关注了如何在UDN中，通过优化的功率控制，来实现网络中高效的干扰协调。但在移动网络场景下，用户移动会使网络中的干扰情况不断变化。在以室内热点覆盖为典型应用场景的UDN中，复杂的室内结构和密集部署的SBS也使得网络中的干扰环境十分复杂。传统的静态优化算法和博弈论等启发式算法难以适应UDN中复杂多变的干扰情况，因此，在动态网络环境下，基站需要根据网络状态和干扰环境的变化，动态调整自己的发送功率，从而降低网络中的干扰，提升传输性能。近来，基于机器学习，特别是强化学习的人工智能算法在移动通信网络中的应用引起了研究者的广泛关注[8-9]。在基于强化学习的智能算法中，网络中的智能决策者可以通过对网络环境的观察和交互，不断改进和优化自身的策略。这为在UDN中，通过动态的功率控制策略实现优化的干扰协调和管理，提供了一种有效的解决手段。

本文主要研究在超密集覆盖蜂窝网中，通过智能高效的动态功率控制，实现优化的网络干扰协调。首先，从网络动态决策的角度出发，将UDN网络中的动态干扰环境下，基站发送功率的动态控制决策问题建模为一个马尔科夫决策过程（MDP）[8-9]。进一步地，基于强化学习的思想，采用 Actor-Critic（AC）算法[8]对 MDP 模型进行求解，并在此基础上，设计了基于AC方法的智能功率控制算法。最后，通过仿真实验验证了提出算法的性能。数值结果显示：与传统的干扰协调算法相比，本文提出的智能功率控制算法能有效降低UDN网络中基站间的干扰，提升网络传输性能。

1 系统模型

1.1 网络模型

本研究考虑的是如图1所示的CRAN架构下的超密集蜂窝网络。如图1所示，网络由1个宏基站（MBS）和M个小站（SBS）组成，网络中有N个SBS用户。在室内覆盖等典型的超密集蜂窝网应用场景下，可以方便地采用C-RAN架构来实现M个SBS的部署，网络由1个中心控制的基带处理单元（BBU）与M个射频单元（RRH）组成。网络中的用户接入到RRH，实现无线射频信号的接入，每个RRH可以看作一个接入小站。BBU为与其相连的RRH提供基带处理资源，实现中心控制的基带信号处理与无线网络资源的分配与优化。为了提高频谱效率，考虑所有的接入站点采用同频部署，每个基站的可用下行传输带宽为B，划分为K条相同带宽的正交子信道，那么每条子信道的带宽可以表示为b=B/K。同一时刻，任一子信道只能分配给一个用户。

为了便于分析，考虑用户在某一时刻只能通过一个接入站点的一条子信道接入网络，设用户n通过基站m的子信道k接入网络，则在t时刻用户获得的服务速率为：

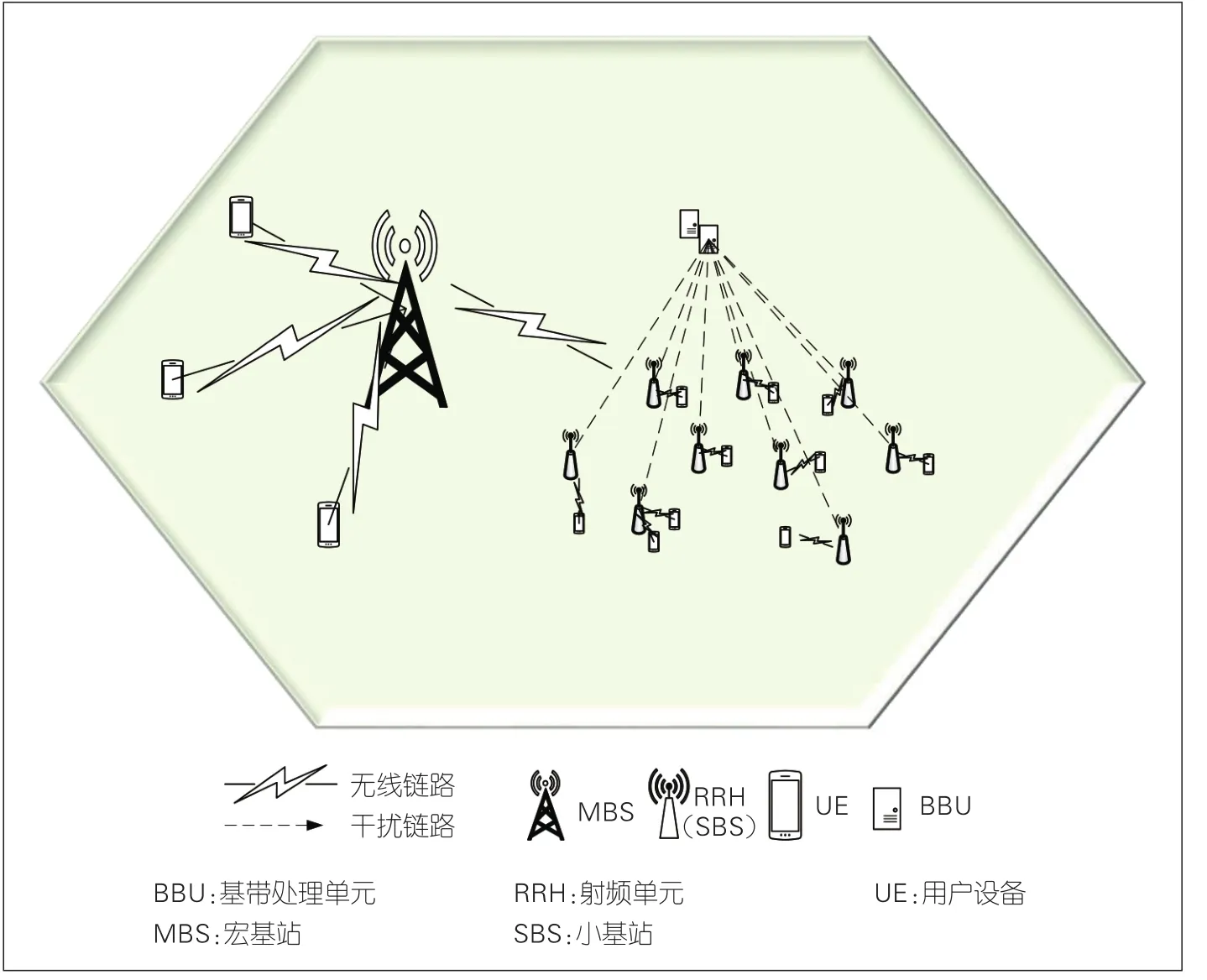
▲图1 基于集中化无线接入网架构的超密集蜂窝网络

1.2 理论模型

从式（2）可以看出，在密集覆盖的蜂窝网中，用户获得的下行传输速率受其接入站点的发送功率、信道增益，以及其他站点产生的干扰的影响；而其他站点对用户的干扰，又由站点的发送功率和用户到该站点的信道增益决定。在动态场景下，用户移动带来信道增益的变化。因此，为了满足用户服务需求，在本研究中，考虑通过动态地调整基站的发送功率，来降低网络中的干扰，提升网络的整体传输性能。

在传统网络中，常常以最大化系统吞吐量作为网络的优化设计目标。但在本文考虑的UDN场景下，不同站点间干扰情况复杂。如果单纯地以最大化系统吞吐量为优化设计目标，可能由于小区边缘用户的信道衰落大，且距离干扰源更近，造成网络为了提升系统整体吞吐量，牺牲边缘用户的传输性能，从而为边缘用户分配较少的发送功率，使得网络中资源分配不公平。在本研究中，我们希望在提升系统整体吞吐量的同时能够兼顾网络的公平性。因此，考虑采用与文献[9]类似的方法，以α公平作为公平性度量，设计一个兼顾网络性能和公平性的效用函数：

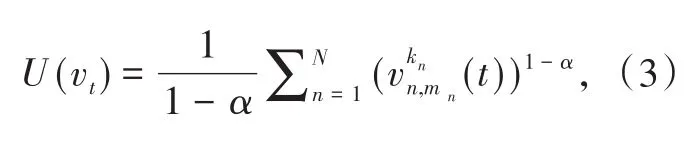
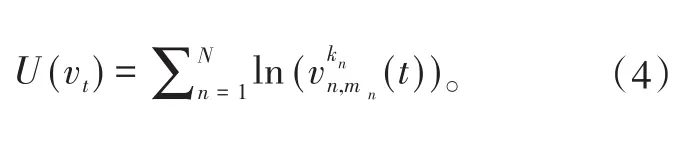
在动态网络场景下，需要通过不断地调整基站发送功率来降低网络中的干扰，提升网络传输性能。因此，不能简单地以某个时刻系统的最大化效用函数来优化设计网络中的功率分配，而应该以最大化系统的长期效用为目标，设计网络中的功率动态优化控制策略。由此，根据式（4）可以将一段较长时间T内，网络中的功率优化分配问题建模为：

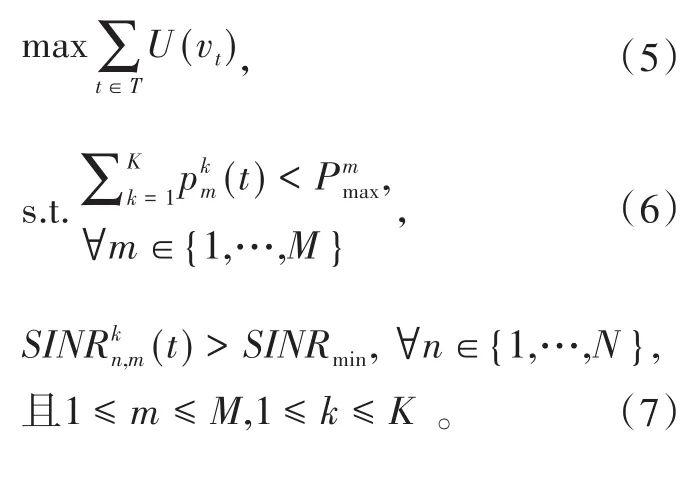
其中，约束条件（6）表示，任一时刻，某一基站m在所有子信道上的发送功率总和不能超过该基站的最大可用功率。而约束条件（7）表示，用户获得的信干噪比不能低于最小接入门限SINRmin。

我们注意到，在问题（5）中，由于信号与干扰加噪声比（SINR）的表达式中包含了其他站点的干扰信号，目标效用函数是非凸函数，并且优化目标为效用函数在时间维度上的累积值，难以采用传统优化方法对该问题进行求解。因此，考虑将问题（5）对应的密集覆盖蜂窝网中的功率动态优化分配问题建模一个马尔可夫决策过程，系统根据网络状态的动态变化来周期性地调整网络中的功率分配策略。在此基础上，采用强化学习的方法对MDP进行求解。

2 MDP建模

在C-RAN网络架构下，BBU可以方便地获得各个分布式RRH的资源使用情况以及接入用户的状态信息，因此，考虑将所有SBS组成的网络系统看作一个智能决策主体，将网络中的基站发送功率的动态优化控制决策建模为一个MDP问题，并用元组(S,A,P,R)表示。其中，S为系统状态空间，A为采取的动作空间，P为状态转移概率，R为回报函数。MDP的各个组成元素具体可以表示为：

（1）系统状态。s∈S表示在当前智能体观察到的系统状态，定义s=表示用户n通过基站mn的子信道kn接入网络所获得的信干噪比，可以由式（2）得到。而则为用户在接入信道上的信道增益。其中，kn∈{1,2,...,K}，mn∈{1,2,...,M}。我们注意到，根据式（2）可知，由基站的发送功率、用户信道增益和用户受到的干扰等因素共同决定。在每个决策周期，用户将自己当前的信干噪比反馈给接入的RRH，再由RRH上报给BBU。而用户在接入信道上获得的信道增益，与用户和基站的距离以及之间是否存在阻挡物等条件相关。在动态网络环境下，这些条件主要受用户行为特征的影响。虽然用户信干噪比受用户信道增益的影响，能够在一定程度上反映信道增益对用户获得的服务性能的影响，但在系统状态中增加信道增益，能够更加直接地反映用户移动带来的网络动态特性对资源分配策略和网络传输性能的影响。由此，系统状态s将随网络中的基站资源使用情况、用户行为以及网络干扰条件的变化而变化。

（2）动作。用a∈A表示智能体采取的动作。定义在每个决策周期，智能体采取的动作为决定每个SBS的发送功率，即其中，为基站m在子信道k上的发送功率，有k∈{1,2,...,K}，m∈{1,2,...,M}。是连续可调的，且如果当前时刻基站m的子信道k上没有接入用户，则对应的

（3）状态转移概率。用P=表示状态转移概率集合。其中，为当系统处于状态s时，执行动作a后，转移到的状态s'的概率。

（4）回报函数。考虑到优化目标为最大化系统的长期效用函数，因此将智能体在每个决策时刻，根据当前状态s采取动作a后取得的即时回报表示为：

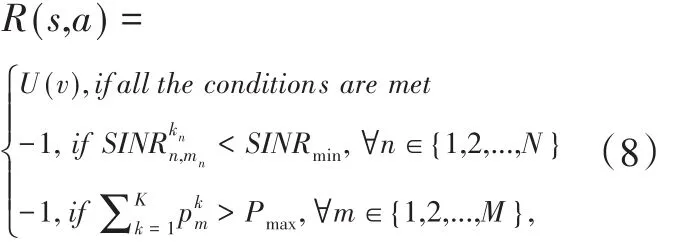
其中，U(v)可从式（4）得到。v={v1,v2,...,vN}为采取动作a后，系统中所有用户获得的传输速率构成的向量，可由式（1）得到。式（8）中后两项为惩罚项，对应（6）和（7）的限制条件。当前决策时刻采取动作a时，如果有用户获得的接入信干噪比低于最低门限SINRmin，或某个基站分配给所有子信道的功率之和超过基站的最大可用功率Pmax，则获得的即时回报为惩罚值-1。

由此，将UDN中的功率动态优化控制问题建模为了一个MDP，所有SBS构成的网络系统作为一个智能决策主体，周期性地根据观察到的网络状态，进行基站发送功率分配的智能决策，以最大化网络的长期累积效用。

在MDP框架下，定义状态值函数来反映当前状态下，智能体采取策略π获得的长期回报，表示为：

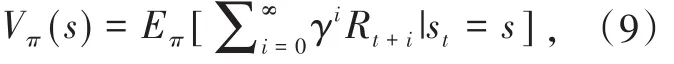
其中，γ为折扣因子，表明未来的回报相对于长期回报的重要程度。相应地，定义动作值函数来表示某一状态下采取某一动作的长期回报，可以表示为：

其中，Eπ[x]表示在策略π下变量x的均值。对于给定的策略π，观察式（9）和（10）可以得到：

其中，π(a|s)为采用策略π的情况下，系统处于状态s时采取动作a的概率。在MDP模型下，系统决策的目标就是找到一个最优的策略π*，使得对应的Vπ(s)和Qπ(s,a)最优。

3 问题求解

在我们定义的MDP模型中，系统状态空间和动作空间都是连续的，且状态转移概率难以获取，因此考虑采用Model-free的AC算法[8]来对MDP模型求解。AC算法是一种将值函数迭代和策略迭代相结合的强化学习算法，其基本框架如图2所示。AC算法主要包括两个执行部分：一个是Actor，用于改进并生成当前执行策略；一个是Critic，用于评估策略执行结果，指导Actor进行策略改进。

（1）Actor。

在AC算法中，Actor通过不断调整策略以改进决策的回报。本文考虑采用高斯正态分布来近似策略分布，则有Actor的参数化策略可以表示为：

其中，μθ(s)和σθ(s)分别为正态分布的均值和方差。考虑采用输入为系统状态s，输出为μθ(s)和σθ(s)的神经网络来对均值和方差进行近似拟合，参数θ对应神经网络全连接层的权重参数。由此，策略的调整就转化为参数的更新，我们期望参数朝着最大化MDP长期累积效用的方向更新。在强化学习框架下，常常使用梯度下降的方法来进行参数更新，可以得到：

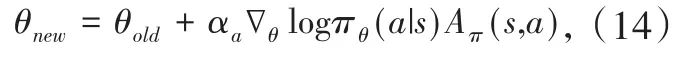
其中，αa为Actor的学习速率，Aπ(s,a)为优势函数。

（2）Critic。

在AC算法中，Critic的作用是通过估计状态值函数来对Actor策略的改进提供指导。在考虑的MDP模型中，由于系统状态空间是连续的，因此同样采用输入为系统状态s、输出为Vξ(s)的神经网络来进行状态值函数的近似拟合，ξ为神经网络全连接层的权重参数。通过参数化的近似后，值函数的更新也可以通过参数的迭代更新来实现。

为了对参数ξ进行更新，时序差分（TD）算法误差被引入：

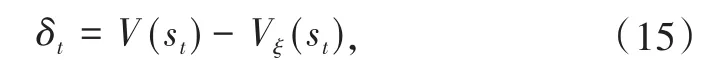
其中，st为决策周期t的系统状态，且有V(st)=Rt+1+γVξ(st+1)。Critic 的目标是尽可能准确地估计值函数，因此其优化目标应该是最小化TD误差，可以表示为：

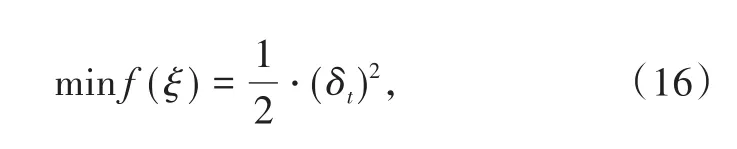
同样使用梯度下降法更新参数ξ，得到：

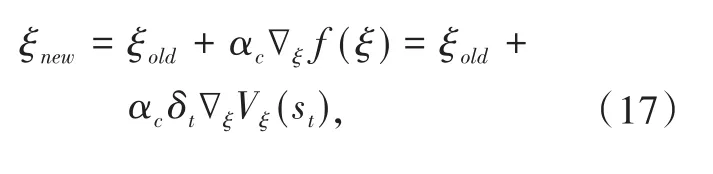
其中，αc为Critic的学习速率。

（3）基于AC算法的基站功率分配机制。

在AC算法中，往往采用公式（13）中的TD误差作为Actor参数更新过程中的优势函数，即令Aπ(st,a)=δt，那么公式（12）可以改写为：

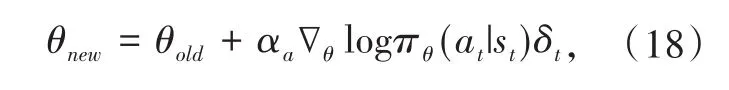
由此，在UDN中，可以利用式（17）和（18），通过参数的迭代更新来优化系统中所有SBS基站的功率分配策略，具体的功率控制算法流程如算法1所示。

αa：Actor的学习速率

αc：Critic的学习速率

αt：智能体在时刻t采取的动作

γ：折扣因子

ACP：基于AC的基站功率控制

K：子信道数量

M：SBS数量

N：SBS用户数

T：周期

TD：时序差分

V：值函数

4 数值结果分析

在本节中，将通过仿真实验验证提出的智能功率控制算法ACP的性能。

4.1 仿真设置

考虑采用如图1所示的密集覆盖蜂窝网络覆盖场景，网络中包含1个MBS和20个SBS。在仿真中，考虑模拟室内覆盖的典型应用场景，所有的SBS位于一栋建筑物内。为了模拟楼层天花板和墙体对无线信号的阻挡，仿真中采用二层住宅楼的建筑结构，而在每一层采用图3中的双线建筑模型[10]。如图3所示，每层包含两排房间，每排5个套房，中间走廊宽度5 m，每个套房的尺寸为10m×5m×5m。每个套房内部结构如图4所示，分为多个房间，用墙体隔开。

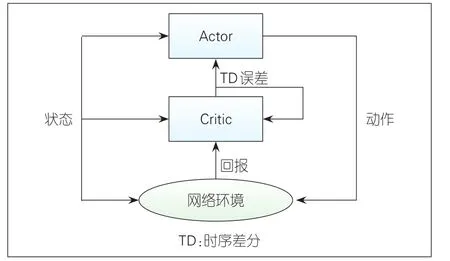
▲图2 AC算法框架

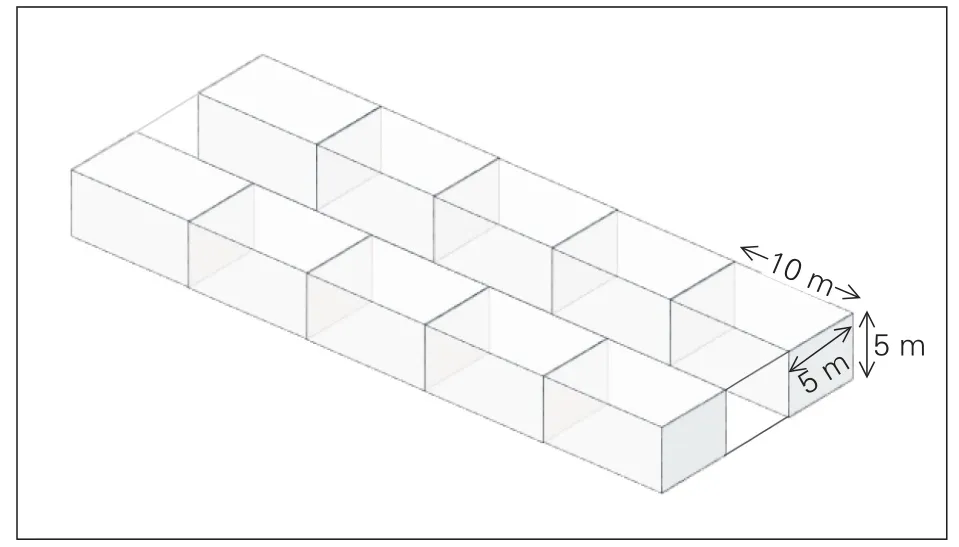
▲图3 双线建筑模型

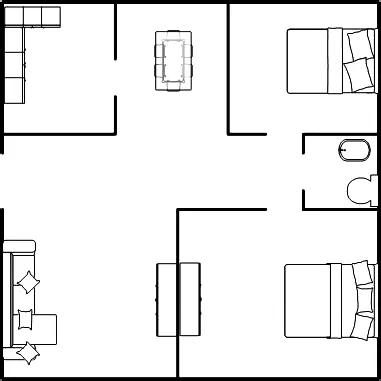
▲图4 房间室内结构

考虑到网络中存在一定数量的MBS用户和SBS用户，所有SBS用户位于建筑物内，以平均1 m/s的速度随机移动；而MBS用户以平均速度5 m/s在建筑物外，MBS的覆盖范围内随机移动。移动过程中，用户随机选定移动方向，当遇到阻碍或到达边界时重新选定移动方向。仿真中具体参数设置如表1所示，同时参考文献[11]，无线信道路损模型如表2所示。在表2中，d为用户到基站的直线距离，din为基站到用户的水平距离。设Low=20dB为建筑外墙穿透损耗，Liw=5dB为室内穿墙损耗。nw为用户和基站之间间隔的楼层数。同时，设置AC算法中学习速率αa=αc=0.01，折扣因子γ=0.2。本节所有的数值结果都是50次独立随机仿真结果的平均值。

在仿真中，选取平均功率分配和软频率复用两种典型的算法作为对比，验证提出的基于AC的基站功率控制（ACP）的性能。两种对比算法的基本思路如下：

（1）平均功率分配（EDP）：每个基站将可用功率平均分配给所有接入用户。

（2）软频率复用（SFR）：将基站的可用频带分为主载波和副载波两部分。主载波服务于边缘用户，副载波服务于非边缘接入用户，根据接入边缘用户的数量确定主副载波所占比例。主副载波具有不同的最大发送功率门限，仿真中限制副载波的最大发送功率门限为主载波一半。

4.2 数值结果

图5给出了ACP算法的收敛情况。如图5所示，智能算法具有明显的收敛特性。在仿真初期，智能算法处于探索阶段。由于经验不足，智能体获得的收益较低，系统性能较差。随着训练次数的增加，算法通过对用户行为与传输环境的探索，逐渐学习到更好的功率分配策略，智能体获得的收益增加，系统性能提升，并最终收敛。从图中可以看到，算法大概在迭代训练5 000次后达到收敛。

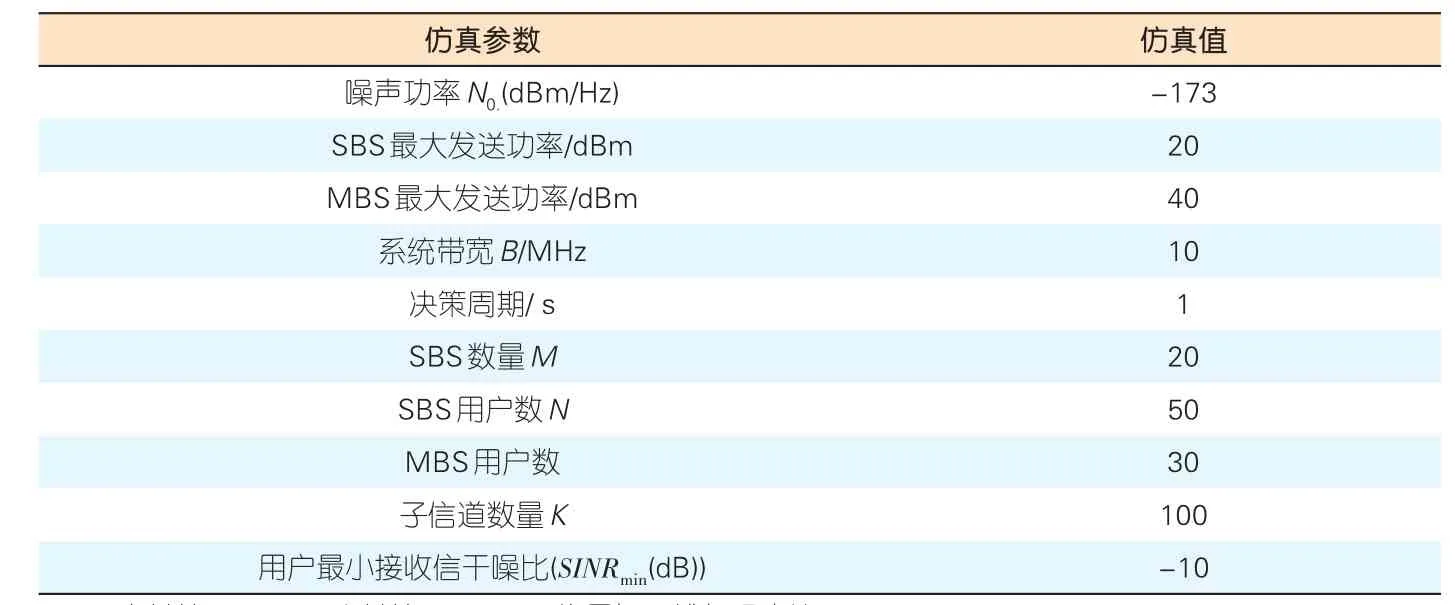
▼表1 仿真参数列表

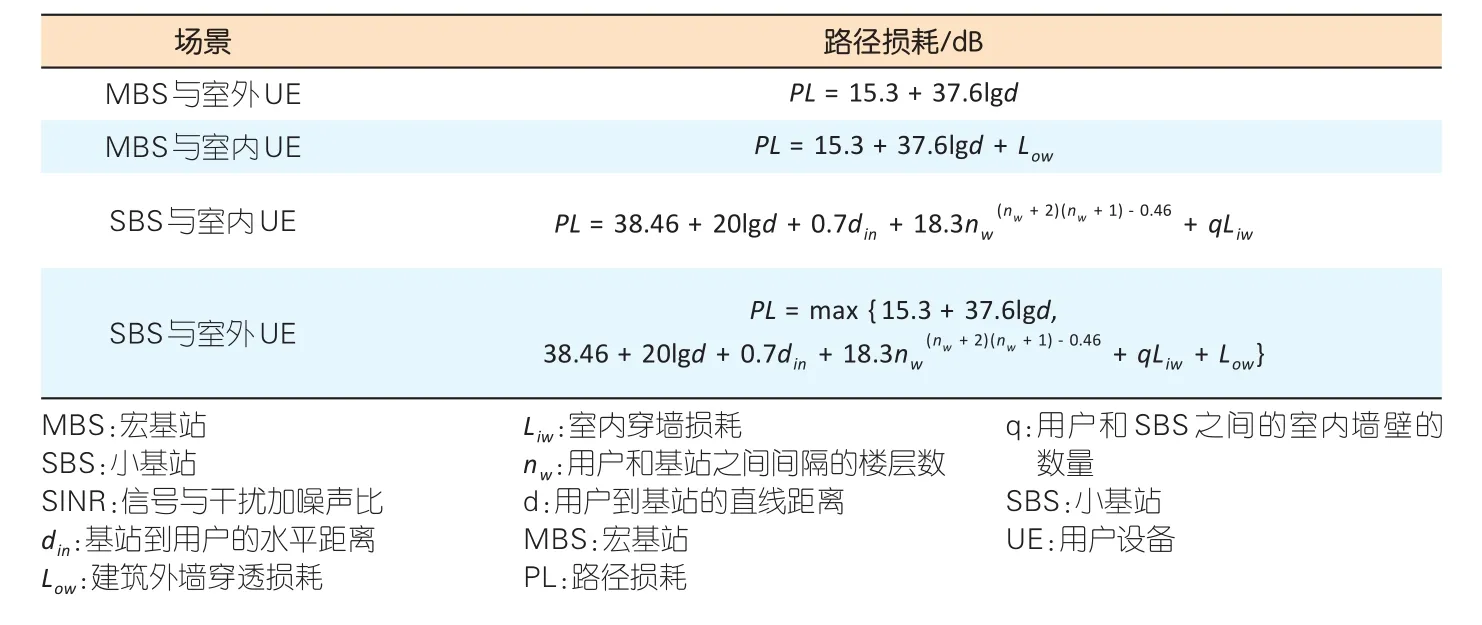
▼表2 路损模型

图6比较了3种不同算法下，网络中所有SBS用户获得的服务速率的概率分布函数。从图中可以看出，与另外两种算法相比，运行ACP算法的SBS用户能够获得更高的服务速率，系统的整体吞吐量也会更高。这是因为在ACP算法中，系统能够通过感知到的网络状态和用户信道条件的动态变化特征，智能地调整基站的发送功率，从而降低网络中干扰，提升用户获得的服务速率。而SFR算法中，采用设置门限的方式，降低了非边缘用户的发送功率，从而降低了网络中的干扰，特别是网络边缘用户受到的干扰；因此，用户能够获得比EDP算法更高的服务速率。

在本文考虑的仿真场景中，采用智能算法的SBS和传统的MBS共存，且相互干扰。图7比较了不同算法下，网络中不同类型用户获得的平均服务速率。如图7所示，采用ACP智能功率分配算法的所有SBS用户的平均传输速率明显优于EDP和SFR算法。同时，虽然MBS没有采用智能功率分配算法，但运行ACP算法的SBS可以根据网络中干扰条件的动态变化，调整自身的发送功率，从而降低对MBS用户的干扰。所以ACP算法下，MBS用户获得传输速率依然高于其他两种算法。由此，在ACP算法下，网络中所有用户的平均传输速率同样优于EDP和SFR算法。

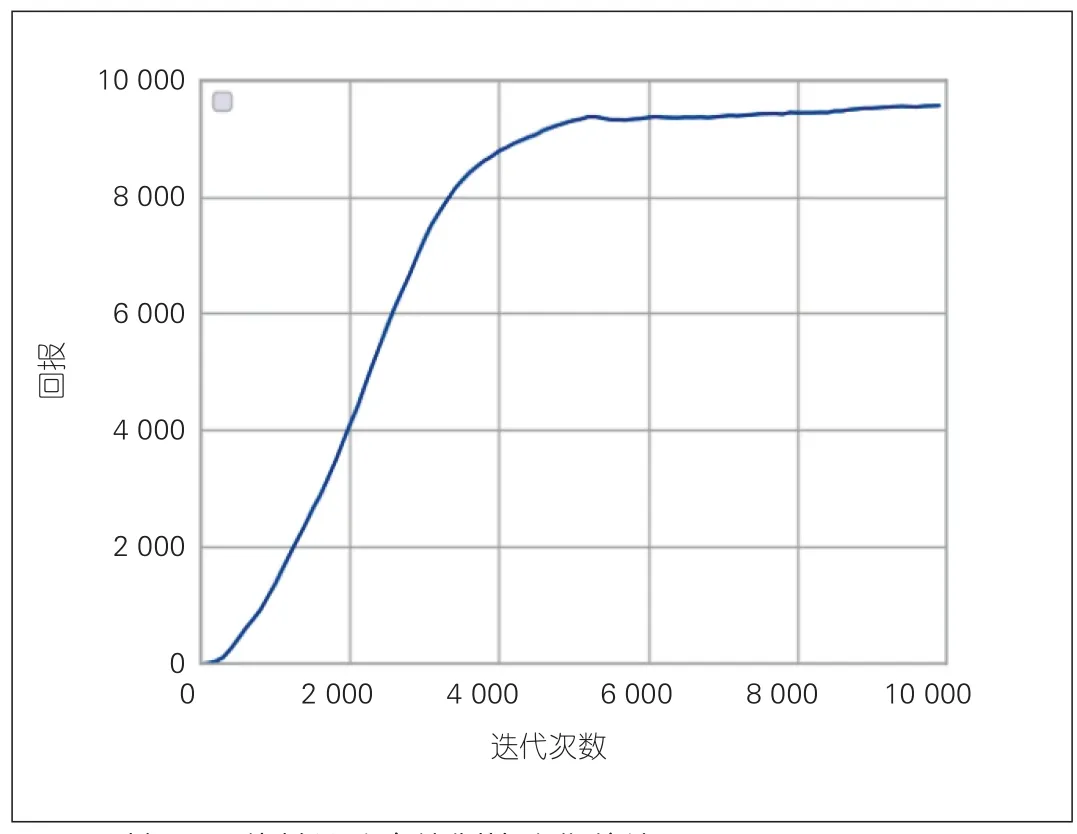
▲图5 基于AC的基站功率控制算法收敛情况

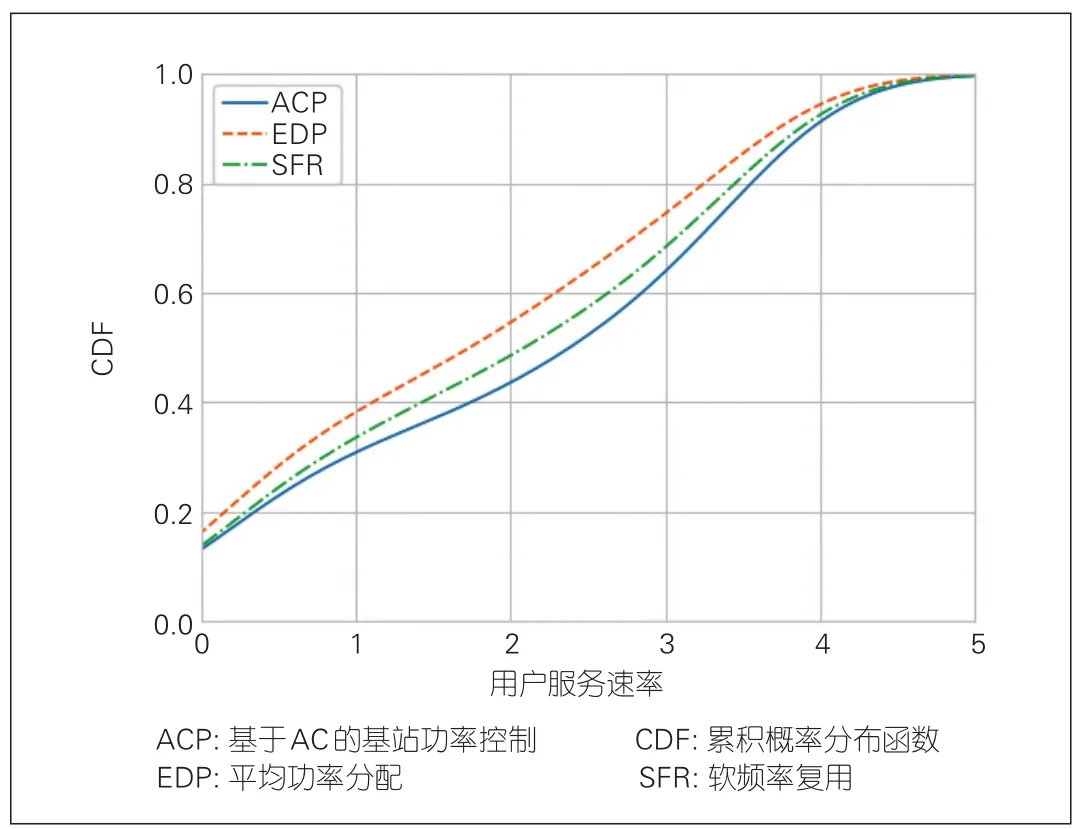
▲图6 用户服务速率累积分布函数

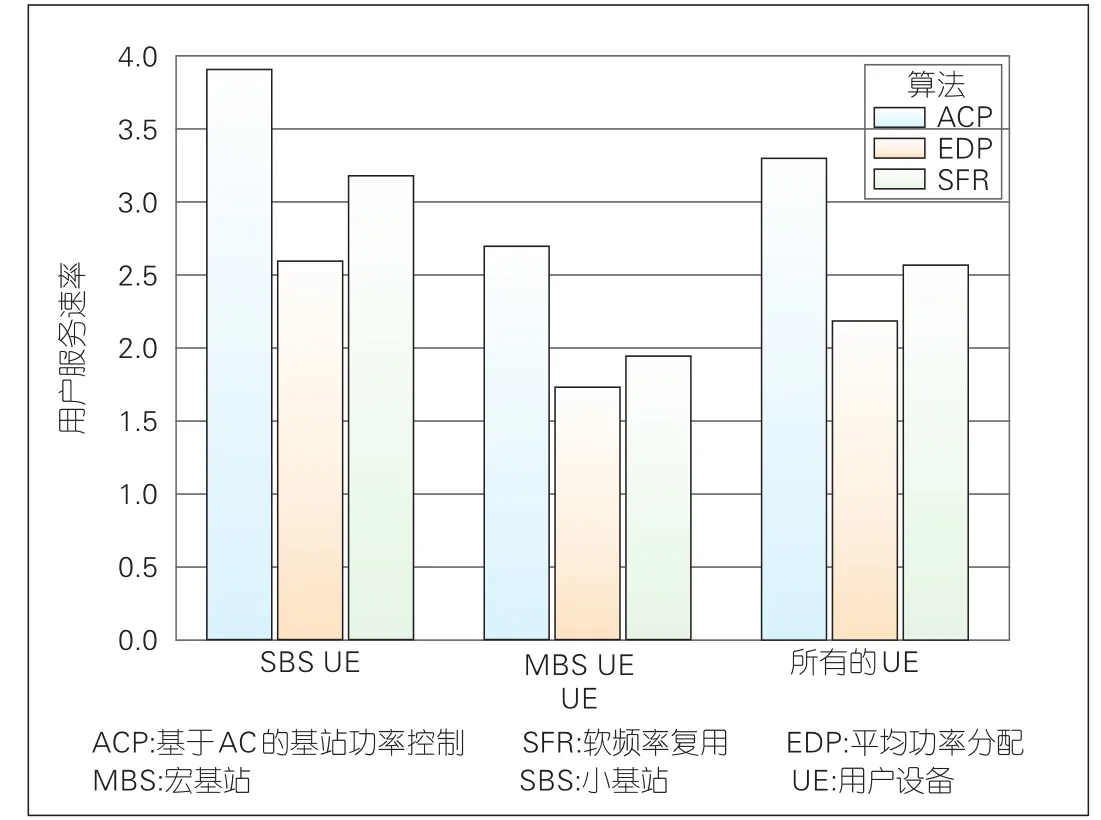
▲图7 用户平均服务速率

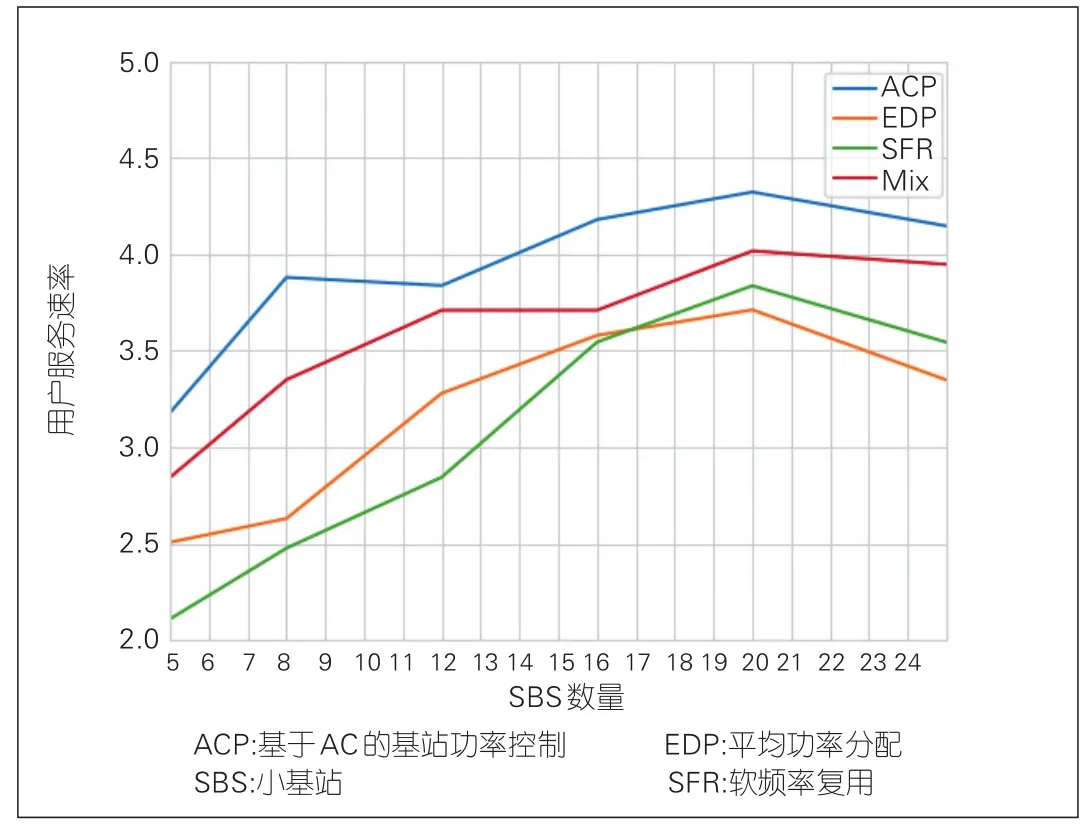
▲图8 用户平均服务速率vs.基站数量

图8为所有SBS用户平均服务速率随网络中基站数量的变化情况。考虑到实际系统中，由于管理权限、部署先后顺序等，在有些情况下可能无法在所有的SBS上采用统一的智能功率控制算法，网络中智能SBS和传统SBS共存。在仿真中，为了验证智能基站和传统基站混合部署情况下网络中的传输性能，增加了一种称为Mix算法的混合功率控制方案。在Mix算法下，一半的SBS采用智能的ACP算法，一半的SBS采用EDP算法。从图8可以看到，当基站数量较少时，随着SBS数量的增加，4种算法下用户获得的平均服务速率增大；但随着基站数量增加，网络中干扰逐渐增大，导致在基站数量较多时，用户获得的平均服务速率反而下降。不论是在哪种情况下，ACP算法获得的用户平均服务速率总是优于其他3种算法。而Mix算法的性能优于EDP和SFR算法，说明智能和非智能SBS混合部署情况下，网络中的传输性能依然优于完全不使用智能功率分配算法的情况。值得注意的是，SFR算法和EDP算法的性能曲线随着基站数量的增加发生了交叉。这是因为，在基站数量较少时，小区间干扰较低，而SFR限制了非边缘用户发送功率，这会导致用户获得的服务速率较低。随着基站数量的增加，小区间干扰变得严重，EDP算法没有任何干扰协调机制，这导致用户的服务速率受到较大影响；而SFR算法限制了非边缘用户的发送功率，降低了网络中的干扰。

5 结束语

本文研究了超密集蜂窝网中的智能干扰协调问题。考虑到移动网络的动态特征，将基站的动态功率控制建模为一个马尔科夫决策过程，并采用强化学习的方法，利用AC算法对其进行求解。在此基础上，设计了一个基于AC的基站功率动态智能控制算法。仿真实验结果证明，该算法能够有效降低超密集蜂窝网络中基站间的相互干扰，提升网络传输性能。