基于Delaunay三角网格的土石混合边坡块石空间分布评价与随机投放方法

吴冠雄, 张宗堂, 杨期君, 柳光磊, 樊宝杰

(1.湖南省茶常高速公路建设开发有限公司，湖南 常德 415000；2.湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室，湖南 湘潭 411201；3.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411201)

1 概述

土石混合体边坡是由粒径较大的块石骨料和粒径较小的土颗粒基质组成的混合介质结构体[1-2]。其块石骨料多为漂石或块石粒，基质多为黏土或沙土等。由于构成土石混合体的块石骨料与土体基质的物理力学性质有很大差别，骨料的几何性质多表现为非均匀、不连续、结构复杂、分布规律性差等特征[3-5]，因此不能采用传统的均匀土质边坡分析方法来进行土石混合体边坡的相关研究。

近几年来，随着现代科学技术的不断发展，许多学者提出通过数字图像处理技术来获取并评价土石混合体块石几何信息的研究方法[6-8]。许多学者先后对块石的含量、形状、粒度组成、空间排列方向等特征进行了详细的评价与分析[9-10]，并提出了建立随机土石混合体数值模型来研究块石几何特征对土石混合体边坡稳定性的影响[11-12]。

然而，在以往的研究中，并未有学者考虑块石空间分布格局的均匀或随机特征，在进行块石随机投放的过程中仅以块石边界不相交作为投放准则进行块石的依次投放，忽略了模拟对象的块石空间分布格局可能存在一定的规律性。

为了能够进一步研究块石空间分布格局对土石混合体边坡宏观工程特性的影响，本文重点对土石混合体的块石分布进行空间格局评价，利用Matlab程序语言开发了随机块石空间分布的土石混合体边坡的几何模型生成系统，为进一步开展数值试验研究奠定了基础。

2 块石分布的空间格局分析

本文以徐文杰[13]等人2008年发表的“基于数字图像技术的土石混合体边坡稳定性分析”论文中土石混合体边坡的矢量模型(见图1)为研究对象来进行块石空间格局分析算法的说明。

(a) 断面照片

2.1 土石混合体体块石的几何中心点识别

由图1可知，在土石混合体边坡的矢量模型中，每个块石都是由若干个相邻的像素点轮廓构成，通过对表征块石颗粒的所有像素点进行坐标标记，基于公式(1)来计算每个块石颗粒的几何中心。

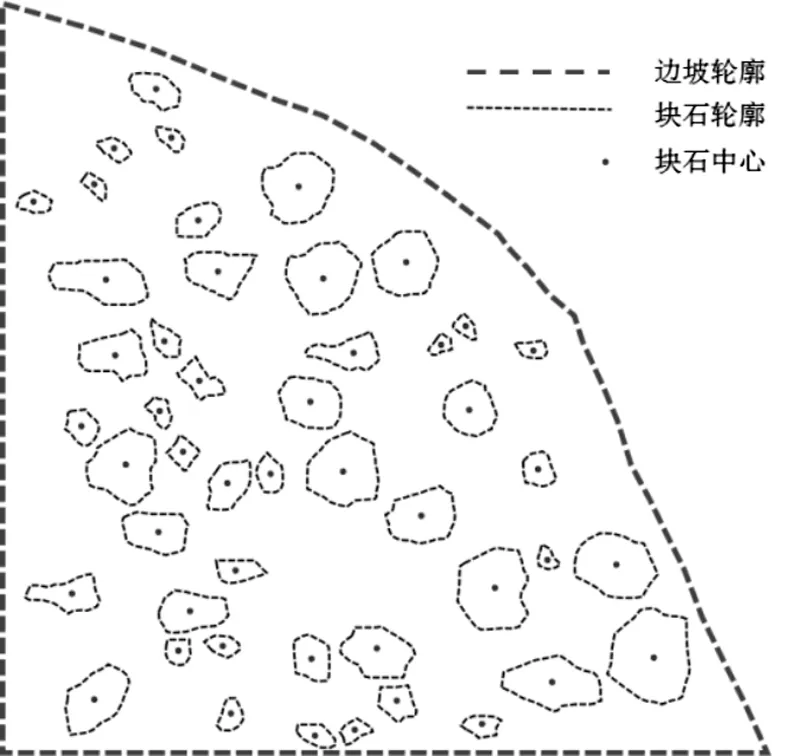
图2 块石的几何中心点识别结果Figure 2 Recognition result of geometric center point of block stone

2.2 Delaunay三角网格划分

点集的三角网格化，对数值分析(比如有限元分析)、图形学以及拓扑学来说，都是极其重要的一项预处理技术。所谓三角网格化是假定平面中有N个点，用互不相交的线段将其连接起来，以致凸包内的每一个区域都是一个三角形。目前三角网格化的普遍性准则是，三角网格化之后，得到那种细长且尖锐的钝角三角形越少越佳，类似等边三角形的锐角三角形越多越佳，整个三角网格均匀性越好越佳。

基于Lawson算法对土石混合体边坡的块石中心点集进行处理，其具体步骤如下：

a.对边坡外轮廓内的块石几何中心点进行识别，得到m个中心点。

b.采用凸包算法，建立一个大的多边形，设该多边形凸包上的n个点构成顶点序列L={p1,p2,p3,…,pn}，剩余凸包内的点构成点集S={q1,q2,q3,…,qn}，见图3。

图3 凸包算法处理结果Figure 3 The result of the convex hull algorithm

c.选取点集S内的第一个点q1，将其插入点集合L中，分别将L内的其他各点与q1连接，形成三角网格链表。

d.选取下一个点q2，将其插入点集合L中，在三角形链表中找出其外接圆包含插入点q2的三角形(称为该点的影响三角形)，删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在Delaunay三角形链表中的插入。

e.根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。

f.循环执行上述第4步，直到所有散点插入完毕。

g.直至完成最后一个点qm-n的插入，得到如图4所示的网格结构。该网格结构中，对象块石颗粒中心与最近邻块石颗粒中心的距离即为构建Delaunay三角网相对应的三角形边长，不需要再进行不同块石颗粒中心点之间距离的逐一计算与排序。

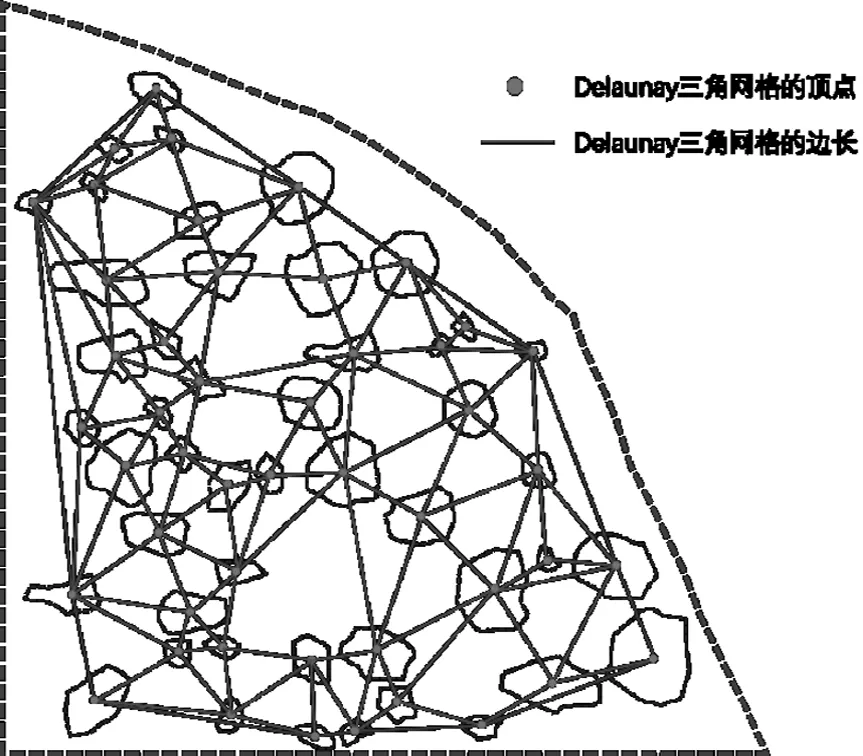
图4 Delaunay三角网格处理结果Figure 4 The result of the Delaunay triangulation mesh

2.3 基于Delaunay三角网格的聚集指数

由本文算法得到的图4中的Delaunay三角网存在以下特性:

a.在Delaunay三角形网中任一个三角形的外接圆范围内不会有其它点存在并与其通视，即空圆特性。

b.在构网时，总是选择最邻近的点形成三角形并且不与约束线段相交。

c.形成的三角形网总是具有最优的形状特征，任意2个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么2个三角形6个内角中最小的角度不会变大。

基于以上理论，可以推出，土石混合体块石(即在所构造Delaunay三角网中表征为每个三角形的顶点)与最临近块石(即为最邻近三角形顶点)的距离必定为三角形的某一个边长。因此，可以通过求取每一个顶点所占边长中的最短距离(以ri表示)来计算能够表征块石分布均匀性的指标，聚集指数R，其计算公式如下：

如图5所示，当R=0时，点为完全聚集分布；当R=1时，点为随机分布；当R=2.149时，点为完全均匀分布。当02.149时，点的分布为极好的均匀分布。对图2中点边坡进行聚集指数计算，其计算结果见为1.131，属于比较接近于聚集的随机分布。

(a) 聚集分布(R=1)(b) 随机分布(01)

3 改进的块石随机投放方法

为了模拟不同空间分布程度的土石混合体边坡，需要改进随机块石投放的效果。本文在进行土石混合体边坡的随机重构时，通过循环算法，采用Delaunay三角网格法对基于蒙特卡罗随机生成的空间散点进行同步处理，直至所生成散点试样的聚集指数与预期匹配则退出循环。并以所生成的Delaunay三角网格的顶点为基础进行颗粒投放，从而生成符合一定空间分布格局特征的随机块石分布模型。生成2种不同程度空间分布格局形式的边坡如图6所示。

(a) 随机分布土石混合体边坡 R=1.0

4 结论

本文以土石混合体边坡为研究对象，以单个块石颗粒的几何中心为平面点构建Delaunay三角网格，采用基于Delaunay三角网格的集聚指数，对土石混合体的块石分布进行空间格局进行了系统的评价。采用Delaunay三角网格法对基于蒙特卡罗随机生成的空间散点进行同步聚集指数评价与匹配，开发了能够自定义块石空间分布格局的土石混合体块石投放模型，为进一步开展了一系列的数值试验研究奠定了基础。