预应力UHPC-T梁抗剪性能试验研究

2020-11-18童汉元刘海波

公路工程 2020年5期

童汉元, 刘海波

(1.湖南大学土木工程学院，湖南长沙 410082；2.湖南省交通水利建设集团有限公司，湖南长沙 410076)

0 引言

超高性能混凝土(UHPC)是1993年由法国Bouygues公司研发的一种新型钢纤维水泥基复合材料[1]， UHPC材料和常规普通混凝土相比，其拥有超高的抗压强度、出色的耐腐蚀性、优异的韧性、低徐变和收缩[2-4]。由于UHPC拥有优异的力学性能和耐久性，因此应用于工程中可以降低截面尺寸、提高跨度以及增加结构的使用周期[5]。目前，UHPC在工程中的应用已经十分广泛，美、日、法、马来西亚等国家都已率先将其应用在桥梁工程领域，国内已有将UHPC应用于人行天桥的实例。UHPC构件的抗剪性能对结构的安全性有着不可忽视的重要影响，为了探究其剪切破坏机理，各国学者展开了一系列试验研究。VOO Y L[6]等研究了预应力、钢纤维形状及其体积含量对预应力RPC无腹筋工字梁抗剪承载力的影响。XU S[7]等研究了剪跨比和纵向钢筋配筋率对UHPC试验梁剪切破坏状态的影响。陈彬[8]等通过10根预应力RPC梁的试验，分析研究了预应力、剪跨比、配箍率等参数的变化对抗剪性能的影响。

目前针对UHPC-T梁的抗剪性能研究并不多，为了更好地将UHPC材料应用在实际工程中，

需要不断深入加强对其抗剪机理的研究。本文通过设计的3根UHPC-T梁试验，对UHPC梁的抗剪性能进行试验研究。在试验结果的基础上，同时结合有限元仿真分析，系统研究配箍率、预应力筋率、张拉应力大小、以及UHPC抗压和抗拉强度等参数对结构抗剪性能的影响。

1 试验概况

1.1 试验梁支座

主要研究UHPC梁的抗剪性能，试验共设计了3根预应力UHPC-T形梁，跨径分别为1.4、2.8、4.2 m。试验梁的截面尺寸以及配筋情况，见表1和图1所示，其中构造钢筋直径为8 mm，预应力筋的张拉应力为1 010 MPa。

表1 试验梁主要参数Table 1 Test results of different failure modes试验梁λρt/%纵筋ρ/%箍筋预应力筋L11.0625ϕ12+8ϕ123.72ϕ12@1002ϕ15.2-4L22.1225ϕ12+8ϕ123.72ϕ12@1002ϕ15.2-4L33.1925ϕ12+8ϕ123.72ϕ12@1002ϕ15.2-4注:表中ρt为钢纤维体积掺入率;ρ为纵筋率。

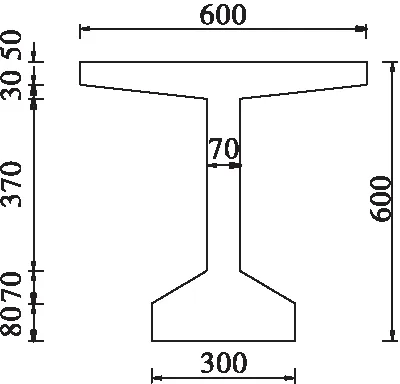
图1 试验梁截面示意图(单位：mm)

试验梁采用钢模板，浇筑完成后待试件初凝(室温下养护48 h)完成后拆除模板，之后在温度90 ℃以上、相对湿度95%左右的蒸汽条件下养护3 d，养护完毕后张拉预应力筋并灌浆。UHPC材料的配合比及力学性能见表2和表3，用于测试力学性能的试块与试验梁由相同材料浇筑、养护。

表2 UHPC基体配合比Table 2 Composition ratio of UHPC matrix组分水泥硅灰石英砂石英粉减水剂水质量比1.0000.2501.1000.3000.0190.2

表3 UHPC材料实测基本力学性能Table 3 Measured mechanical properties of UHPC MPa材料参数弹性模量立方体抗压强度抗折强度参数值42 60012621.7

图2 试验梁加载装置示意图Figure 2 Schematic diagram of loading device for test beams

试验梁采用单点加载，加载装置是液压千斤顶，试验初期以50 kN为一级进行加载，在试验梁进入非线性破坏状态后，采用位移加载。在加载过程中记录位移、荷载、腹板应变、裂缝等试验数据。

1.2 试验结果

试验梁结果如表4所示，表中是开裂荷载，是破坏荷载。试验梁L1～L3的破坏形态分别为斜压、剪压、斜拉破坏。

表4 不同破坏形态的试验结果Table 4 Test results of different failure modes试验梁λVcr/kNVmax/kN破坏形态L11.067682 800斜压破坏L22.123021 690剪压破坏L33.194101 622斜拉破坏

a.试验梁裂缝破坏示意图。

本次3根试验梁破坏的裂缝分布状态如图3所示，试验梁L1破坏时左侧的腹板处被局部压碎，没有形成贯穿截面的临界裂缝，其右侧只出现稀疏的斜裂缝，破坏形态为斜压破坏；试验梁L2破坏时在支座和加载位置之间形成贯穿的斜裂缝，顶板上缘的混凝土被压碎，属于剪压破坏；试验梁L3破坏时加载位置上翼缘混凝土被压碎且底缘出现受弯裂缝，右侧腹板出现两条明显的临界斜裂缝，破坏形态为斜拉破坏。

(a) 试验梁L1

b.荷载-挠度曲线。

3根试验梁加载截面的荷载-挠度曲线如图4所示，在加载初期3根试验梁的变形基本都是线性变形，继续加载后试验梁逐渐进入非线性变形阶段。由曲线可知，试验梁L1～L3的刚度是依次降低的，相应的承载力也逐步下降，试验梁的最大挠度依次为6.7、13.1、25.6 mm。

图4 试验梁荷载-位移曲线Figure 4 Load-deflection relationship of specimens

c.剪跨比影响分析。

3根试验梁的主要不同参数是剪跨比，图5为荷载-剪跨比的曲线。由图5可知，当剪跨比由1.06变为2.12时，承载力的下降幅度为39.64%；而剪跨比由2.12为3.19时，承载力的下降幅度为4.58%。由此可知，剪跨比是试验梁的承载力以及影响破坏形态的重要因素之一。当剪跨比小于2时其对承载力的影响较大；反之，其对承载力的影响明显降低。

图5 荷载-剪跨比曲线Figure 5 Load-shear span ratio curve

2 有限元分析

2.1 模型建立

试验梁的有限元分析模型由ABAQUS软件建立，采用混凝土损伤塑性模型(CDP)进行分析计算。UHPC、支座以及钢垫板均采用C3D8R单元模拟，钢筋和预应力筋采用T3D2单元模拟。在约束模拟方面，支座和梁体采用绑定约束(Tie)，钢筋和梁体采用嵌入约束(Embedded)，网格的尺寸为5 cm，分析步按照实际试验加载方式模拟，有限元模型如图6所示。

(a) 试验梁L1有限元模型

2.1.1UHPC本构关系

在ABAQUS计算分析时，需要对材料的本构关系进行定义，钢筋采用理想弹塑性本构，UHPC由于是新型材料，需要针对其实际受力特性进行定义，具体如下：

UHPC的受压本构关系采用文献[9]提出的公式，如式(1)所示。

(1)

式中：ε0=3 500 uε; ξ=ε/ε0; n=Ec/Eg，其中，Ec为初始弹性模量;Eg为峰值点的割线模量。本文中fc=126 MPa，Ec=42 200 MPa。

UHPC的单轴受拉应力-应变关系采用文献[10]提出的本构，如式(2)所示。

(2)

式中：fct为UHPC应力;εt0为弹性峰值应变;εtp为极限应变。上述参数模型中分别为：fct=8 MPa，εt0=200 με，εtp=1 741 με。

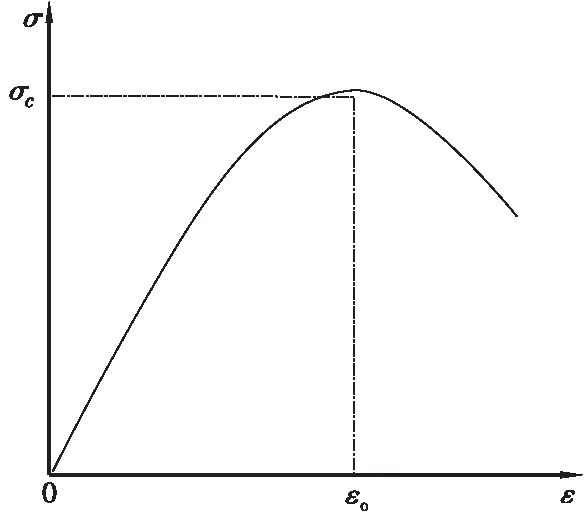
(a) UHPC受压本构

2.1.2CDP材料模型参数

CDP模型需要分别定义UHPC的弹性和塑性两部分的材料参数，弹性参数包括弹性模量Ec和泊松比ν，塑性参数包括膨胀角、偏心率、强度比、双轴与单轴抗压强度比、粘聚系数等，参考文献[11]，各参数取值见表5。

表5 UHPC损伤塑性模型塑性破坏准则参数Table 5 Plastic parameters f of UHPC膨胀角偏心率强度比fKc粘聚系数30°0.11.164.50.000 5

2.1.3UHPC拉、压塑性参数表

ABAQUS需要定义UHPC的单轴受压应力-应变关系，本构关系由弹性段、强化段和软化段组成。弹性极限一般取σc,e 0=fc/3，当混凝土进入非线性段后，其非弹性性应变εc,in与应力关系如式(3)所示：

εc,in=εc-σc/E0

(3)

式中：E0为混凝土的初始弹性模量；εc、σc分别为混凝土的应变和应力。由于试验没有循环加载，故不定义UHPC的损伤参数。UHPC的塑性参数如表6所示。

表6 UHPC塑性损伤模型参数表Table 6 UHPC damage plastic parameter受压参数受拉参数压应力/MPa非弹性应变/10-6拉应力/MPa开裂应变/10-654.00 0.00 8.0058.38 16.61 8.01 74162.44 20.43 66.47 24.82 70.48 29.84 74.46 35.56 78.40 42.08 82.31 49.51 86.17 57.97 89.99 67.60 93.74 78.60

2.2 有限元分析结果

共有3个有限元模型，分别按照上文进行了参数设置，对试验梁进行了非线性分析，有限元分析与试验结果对比如图8所示。

图8 有限元与试验结果对比Figure 8 Comparison of finite element results with experimental results

由图8可以看出，3根试验梁的有限元计算结果和实际试验破坏荷载结果吻合良好，其相对误差均在7%以内，从以上结果可以说明有限元分析可以较好地模拟试验梁的抗剪受力过程。

3 有限元参数分析

上述计算分析证明了建立的有限元模型的准确性与合理性，因此可以通过该模型进行参数分析，确定影响UHPC梁抗剪承载力的主要因素。

由于结构设计时一般要求结构破坏时是延性破坏，故主要针对试验梁L2进行参数分析，确定纵筋率、配箍率、预应力筋数量等参数对抗剪承载力的影响，进而为UHPC结构抗剪设计提供参考和依据。

3.1 预应力筋率

为了研究预应力筋面积对试验梁的抗剪性能影响，在有限元模型的基础上，其他参数不变仅改变底部预应力筋面积。研究分别布置6、8、10和12根预应力筋时预应力UHPC-T梁的抗剪性能，其极限抗剪承载力如图9所示。

由图可知，增加预应力筋数量对抗剪承载力的提高是有限的，预应力筋有6根变成8根时，抗剪承载力提高了约4.3%，8根变成10根时抗剪承载力提升了约2%，继续增加预应力筋数量抗剪承载力基本不在增加。

图9 预应力筋数量对抗剪性能的影响Figure 9 Effect of the number of prestressing tendons on shear behavior

3.2 纵筋率

为了研究纵筋对试验梁的抗剪性能影响，以纵筋直径为唯一可变参数，将纵筋的直径分别设置为Φ10、Φ12、Φ14、Φ16、Φ18、Φ20，分析其对预应力UHPC-T梁抗剪性能的影响，其计算结果如图10所示。

由图10可知，增加纵筋直径对抗剪承载力的提高十分微小，纵筋直径每增加一级，其抗剪承载力的增加基本在1%～2%之间，因此纵筋对结构抗剪性能的影响不大。

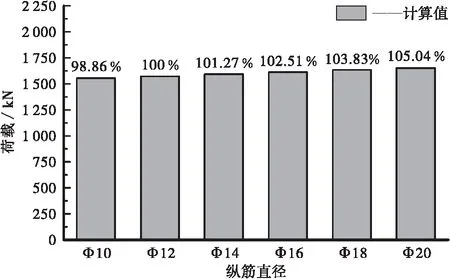
图10 纵筋对抗剪性能的影响Figure 10 Effect of longitudinal bars on shear behavior

3.3 配箍率

为了研究箍筋对试验梁的抗剪性能影响，以箍筋直径为唯一可变参数，将箍筋的直径分别设置为Φ10、Φ12、Φ14、Φ16、Φ18、Φ20，对比计算不同有限元模型的结果，分析箍筋对抗剪承载力的影响，其结果如图11所示。

由图11可知，箍筋直径每增加一级，其抗剪承载力增加幅度约为5%，由此可见箍筋对抗剪承载力的提升明显优于纵筋，其对结构抗剪性能的影响较大。

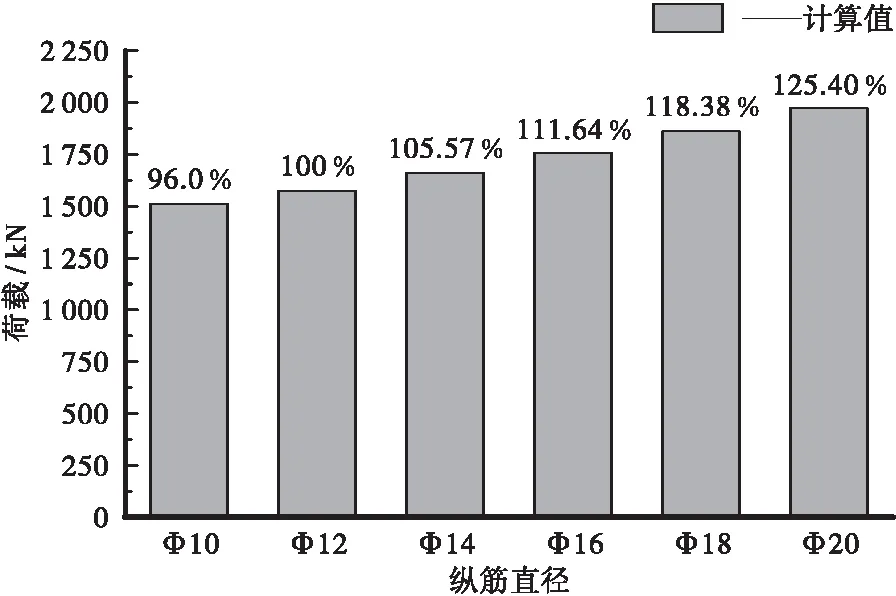
图11 箍筋对抗剪性能的影响Figure 11 Effect of stirrups on shear behavior

3.4 UHPC抗拉强度

将UHPC抗拉强度作为唯一参数变量，UHPC抗拉强度分别设置为6、8、10、12 MPa，分析该参数对结构的抗剪承载力的影响，其结果如图12所示。

由图12可知：改变抗拉强度对结构的抗剪性能影响较大，抗拉强度每增加2 MPa，抗剪承载力约增加8%。

图12 抗拉强度对抗剪性能影响Figure 12 Flexural behavior of beams with different tensile strength of UHPC

3.5 参数的分析

通过有限元模型计算，分析了预应力筋率、纵筋率、配箍率、UHPC抗拉强度等参数变化对结构抗剪承载力的影响。由计算结果可以看出，预应力筋对抗剪性能的影响不大，主要原因是本文试验梁的预应力筋没有弯起，无法有效提供抗剪承载力，弯起预应力筋对抗剪承载力的影响还需要进一步研究；纵筋对抗剪承载力的影响是较小，增加纵筋率对承载力的提升十分微弱；箍筋对抗剪承载力的影响较大，增大配箍率可以很明显提升承载力；UHPC的抗拉强度对结构的抗剪性能影响也十分显著，由于UHPC抗拉强度受钢纤维含量、几何形状以及试件养护方式等多种因素影响[12-13]，为了确保结构的抗剪性能，需要优化UHPC的配合比以及提供良好的养护条件。