供热管网运行数据异常校正方法研究

2020-11-18郭佳昌薛普宁周志刚

煤气与热力 2020年11期

郭佳昌，兰芸，薛普宁，周志刚，刘京

(1.哈尔滨工业大学建筑学院，黑龙江哈尔滨150006；2.哈尔滨工业大学，寒地城乡人居环境科学与技术工业和信息化部重点实验室，黑龙江哈尔滨150006；3.中国中车长春轨道客车股份有限公司，吉林长春130062)

1 概述

21世纪的互联网时代，信息化发展成为我国供热行业发展和进步的焦点，其中信息采集和传输已经成为供热系统不可或缺的一部分。但目前对于这样海量的“大数据”，利用方式仍停留在简单的统计分析阶段，没有让这些数据体现真正的价值。供热数据深度挖掘的实现，不仅对数据数量有所要求，数据质量也必须有所保证，因此在供热系统运行数据库中筛选异常数据，进一步甄别数据异常的真伪，研究数据校正是实现供热大数据真正价值的基础，对于供热“智能化”和“智慧化”发展有着重要的意义。本研究的目的在于探寻供热管网数据采集系统上传信息的数据校正方法，识别出其中含有的错误信息，并将其值修正至合理范围。校正后的数据应能够更准确地描述供热管网实际运行状况，以便研究人员对数据进行更深入的信息挖掘，获得难以观察的管网运行规律，优化调节方案以及诊断系统故障等。

在暖通空调领域，许多学者也开展了数据校正技术的研究。崔治国等人[1-2]提出了1种基于k-means聚类算法的空调运行数据判别方法。Chen等人[3-5]则在研究空调系统冷水机组故障诊断问题时提出将小波分析用于数据去噪处理的方法。吴蔚沁[6]结合了阈值法和k-means算法进行数据异常标定和识别，采用KNN算法进行异常修复，构建了1套公共建筑能耗监测数据校正方法。杨东雄[7]提出了1种基于BP神经网络和k-means聚类算法的误差甄别方法。李思璐[8]则遵循着化工领域数据校正技术的发展路线，研究比较了3种非稳态系统数据在线校正的方法，并得出了中值滤波法更适用于供热管网数据的过失误差侦破。

为了实现供热管网中异常数据的校正，本文建立空间管网水力计算模型对运行数据源进行拓展，根据仿真所得数据源建立基于孤立森林的异常检测模型以及基于BP神经网络的异常识别模型，对异常数据进行替换。然后，基于训练后的模型对实际工程数据进行验证。

2 研究方法

2.1 水力仿真模型模拟运行数据集构建

① 水力仿真模型

通过建立供热管网的水力计算模型，可以仿真不同的运行工况，由此获得符合热网运行规律且完备合理的拓展数据集，可以为数据校正方法提供数据基础和评估依据。

实际供热系统是由热源、供水管网、回水管网和热力站(热用户)组成的空间管网。根据图论理论，可以将其简化为只包含管段和节点2类元素的有向连通图。管段是管网中流量和管径均不发生变化的管道。节点是管段的端点，也是一些管段的交点。恒定流动的供热系统的水力工况满足基尔霍夫第一定律(质量守恒)和第二定律(能量守恒)，即与任一节点相关联的所有管段的管段流量代数和等于该节点的节点流量，以及任一回路的管段压降代数和为0。基于此，可以构建如下水力仿真模型[9]，见式(1)～(7)：

AG=Q

(1)

BΔP=0

(2)

ΔP=ΔPw-ΔPp

(3)

ΔPw=SGdiaaG

(4)

ΔPp=C0+C1G+C2GdiaaG

(5)

式中A——基本关联矩阵，n-1行，b列。其中n表示供热系统的节点数目，b表示管段数目

G——管段质量流量列向量

Q——节点质量流量列向量

B——独立回路矩阵，b-n+1行，b列

ΔP——管段压力降列向量

ΔPw——管段阻力损失列向量

ΔPp——水泵扬程列向量

S——管段阻力特性系数对角矩阵

Gdiaa——管段质量流量的绝对值对角矩阵

C0——水泵特性系数列向量

C1，C2——水泵特性系数对角矩阵

矩阵A中元素aij的取值为

(6)

矩阵B中元素bkj的取值为

(7)

② 运行数据集的构建

利用式(1)～(7)对3类运行工况进行水力仿真，研究不同工况下管段流量与节点压力的变化特征。构建供热系统见图1。该供热系统是由1个热源和6个热力站构成的环状供热系统，其中ni为节点名称，P为热源名称，ui为热力站名称。管段数目b为25，节点数目n为14。管段的水流方向以及环路的方向见图2。热源及热力站的设计参数包括设计流量、热源内部阻力损失以及管段设计阻力系数。供回水管段的设计参数包括管段长度、管段直径、局部阻力折算系数以及管段设计阻力系数。供热系统通常在热源和各热力站安装有流量、压力传感器，因此，本文选取热源质量流量、供水压力以及各热力站一次侧质量流量、一次侧供、回水压力构建运行工况数据集。

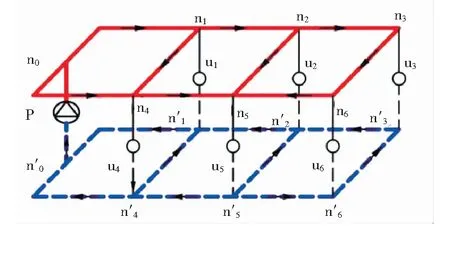
图1 供热系统

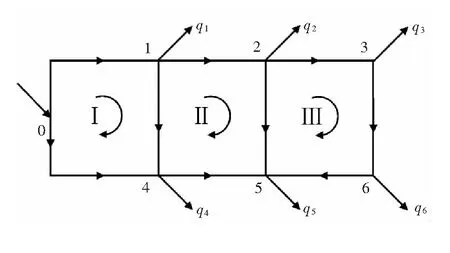
图2 算例平面图

3类运行工况指：热源集中运行调节、热力站局部调节以及管网泄漏。

首先通过改变循环水泵调速比来模拟集中运行调节方案。此外，在热源集中运行调节方案两个相邻阶段之间，增添过渡调速比的工况，来模拟集中调节的过程。

改变热力站阻力特性来模拟热力站局部调节。对不同的管段和节点设定漏水率，来模拟节点与管段泄漏。对正常工况数据组替换其中某几个(不超过5个)元素为随机数，来模拟粗大误差。添加的随机误差符合高斯分布。

2.2 基于孤立森林的数据异常检测模型

① 用于孤立森林异常检测模型的数据集构建

采用2.1节中的数据集构建方法，构建管网模拟运行数据集，称为数据集A，包含4 349条数据记录，每条数据记录包含6个热力站和热源的管段质量流量和供回水压力共20个数据。其中有211条异常数据记录，由于运行工况变化导致的过程异常数据记录共158条，随机添加粗大误差的测量异常数据记录共53条。

② 孤立森林异常检测模型

建立基于孤立森林的数据异常检测模型可以从数据集中挖掘出异常的数据。孤立森林通过孤立对象来检测异常，而不依赖任何距离和密度的测量和计算。它的算法选择的是一种二叉树结构，称为“孤立树(iTree)”，异常对象易受孤立，因此更容易被隔离在孤立树的根部附近，即终止路径长度更短，而正常点更容易被隔离在孤立树更深层。这就是使用此方法检测异常的方法基础[10]。根据模拟运行数据集，以热力站u1的所在管段质量流量以及进出口节点压力为研究对象，其供热运行数据记录4 349条，异常数据占比约5%。

从模拟运行数据集中抽取每条数据中热力站u1的管段质量流量、入口节点压力和出口节点压力，构成数据集B。

模型的构建分为训练阶段和评估阶段。训练阶段，先从数据集B中随机抽取一部分数据作为子采样，用子采样数据构造孤立树。子采样大小φ为256[11]，孤立树数量t为100，样本污染率为10%。

评估阶段，将数据集B作为待检测的数据遍历孤立树，计算观测对象在不同孤立树的终止路径长度，即样本点从孤立树的根节点到最后一片叶子节点所经历的边的数量。然后集成所有树，计算平均路径长度，即样本点经历所有孤立树后终止路径长度的平均值。最后对平均路径长度归一化处理后，得到该条记录的异常分数。最后将所有数据记录按照异常分数从高到低排列，把异常分数较高的440条数据记录列为可疑数据对象，进一步探究其异常形成机制。

对于孤立森林算法模型的评价采用受试者工作特性曲线，简称ROC曲线[12]，见图3。它是以误诊率(FPR)为横坐标，真正类率(TPR)为纵坐标，其中TPR反映的是在所有实际为异常的样本中，被正确地判断为异常的比率。FPR反映的是在所有实际为正常的样本中，被错误地判断为异常的比率。ROC曲线是通过改变异常分数的分数线生成的。ROC曲线上面的每一个点对应的是一个特定的异常分数线，高于异常分数线的记录，认为是异常数据，反之则为正常数据。ROC曲线越靠近左上角说明分类模型的准确性越好。

图3 基于孤立森林的异常检测模型的ROC曲线

AUC值的定义为ROC曲线下的面积，一般为0.5～1。不同分类模型的ROC曲线可能交叉，难以比较分类结果优劣，用AUC值可以更直观地获知哪个模型的分类效果更好。模拟运行数据集采用孤立森林方法分类后计算得AUC值为0.978，说明建立的模型对于异常检测的分类效果很好。

2.3 基于BP神经网络的数据异常分类模型

建立基于BP神经网络的数据异常分类模型，可以对经过异常检测模型获得的怀疑对象，进一步探究其背后的异常机制，以筛选出非供热管网因素导致的真正的异常。BP神经网络处理模式识别问题从数学本质上来讲就是构建一种输入与输出之间的映射，而映射关系无需明确的数学表达，神经网络模型通过对训练样本的学习，掌握其中的映射关系，测试样本输入训练好的神经网络模型就可以得到正确的输出结果[13]。

本文采用含有3隐层的5层BP神经网络结构。输入层代表数据入口，负责接收输入数据，输出层代表模型出口，负责神经网络的预测结果输出。隐层连接输入层与输出层，对输入向量进行特征提取，坐标变换后构成新的向量传递至输出层决策输出结果。参数更新过程中，加入一个新的参数η，称为学习率，学习率在接近最优值过程中不断减小，则网络可以收敛到最优点附近更小的区域。本文中采用指数减缓的措施调整学习率，初始学习率设置为0.01[10]。

选取热力站u1与邻近热力站u2和u4以及热源P为观测点，将非正常运行工况下或者含有随机添加粗大误差的情况下，与正常运行工况相比的节点供、回水压力变化率和所在管段的质量流量变化率作为神经网络的输入，其中热源回水压力作为定压点，取0，因此输入层节点数为4个观测点的3组数据共12个。对于隐层节点数的确定原则是[10]：在满足误差精度要求的前提下采用尽可能简单的结构，即隐层节点数尽可能地小，本文中根据模型复杂程度取经验值。神经网络的输出层具有一个输出单元，输出的是数据异常模式编码，输出编码与异常模式的对应规则见表1。故本神经网络结构为5层神经网络，各层节点数为：12、10、10、5、1。为了避免不必要的数值问题并加速网络的迭代收敛过程，对神经网络的输入与输出数据进行归一化处理。本文中神经网络输入的数据均采用相对变化率的无量纲数，输出则是整数数值，因此采用最大-最小标准化对数据进行归一化处理。本文选用ReLU函数作传递函数，权值初始化方法采用MSRA初始化。误差函数选择交叉熵函数。

表1 神经网络输出编码规则

神经网络数据样本集的构造方法同2.1节，异常模式为1、2、3、4的数据组数分别为60、528、528、200,将该数据集称为数据集C。对200组正常工况水力计算结果，随机添加粗大误差并计算变化率，构造异常模式为4的数据样本。取各类异常模式数据总量的70%构成训练集，剩余30%做测试集。

对测试集的分类结果在200次迭代计算中误差不断减小，经过150次迭代后计算已经收敛，迭代误差精度小于1×10-9，满足计算要求。4种异常模式的分类正确率均达到90%以上，说明模型训练成功，异常分类性能良好。

对2.2节u1热力站测试数据经过孤立森林异常检测输出的440条异常数据记录，从模拟运行数据集中调取对应的热源、u2和u4热力站的数据记录，计算各参数的变化率，构成u1热力站异常分类模型验证集，称为数据集D。

将验证集输入训练好的神经网络模型进行异常分类，验证集的分类正确率结果见表2，总体分类正确率为90.3%，与测试样本集上模型分类的效果相比有所降低，说明模型将所学应用到新的环境条件时分类结果有所偏差，但总体达到90%以上，可以满足工程需求。

表2 神经网络模型在验证集上的分类正确率

2.4 异常数据均值替换

对异常模式为4的异常数据进行替换就可以完成数据校正所有步骤。因为供热系统稳定运行在某个工况时，管网各处的水力参数观测值在时间序列上也是稳定或者围绕真值小幅度波动的，因此，异常值前后时刻的数据对于需要替换的异常值具有很大的参考价值。因此选取异常值所在序列前后各5个邻近序列的数据记录，计算各属性的平均值替换异常数据。

3 基于实际热网数据源的数据校正方法应用

3.1 实际热网数据源组成

以某一实际集中供热系统验证该数据校正方法。该供热系统包含1个供热首站和54个热力站。研究对象选用编号为15的草埠站数据进行校正，热力站所在的局部管网拓扑结构见图4。数据记录以小时计，从2017-11-15至2018-02-03共取得1 944组。选取图中东轸站和银海熙岸站两处热力站为观测对象，用于BP神经网络。在训练基于BP神经网络的异常分类模型时，由于供暖期数据采集时间较短，所获取的数据集中包含的工况变化较少，为了验证本文中提出的数据校正方法的有效性，此处按照2.1节人工数据集的拓展方法，随机添加管网非正常运行工况水力仿真结果至原始数据，拓展后的数据集共包含数据记录1 994条。

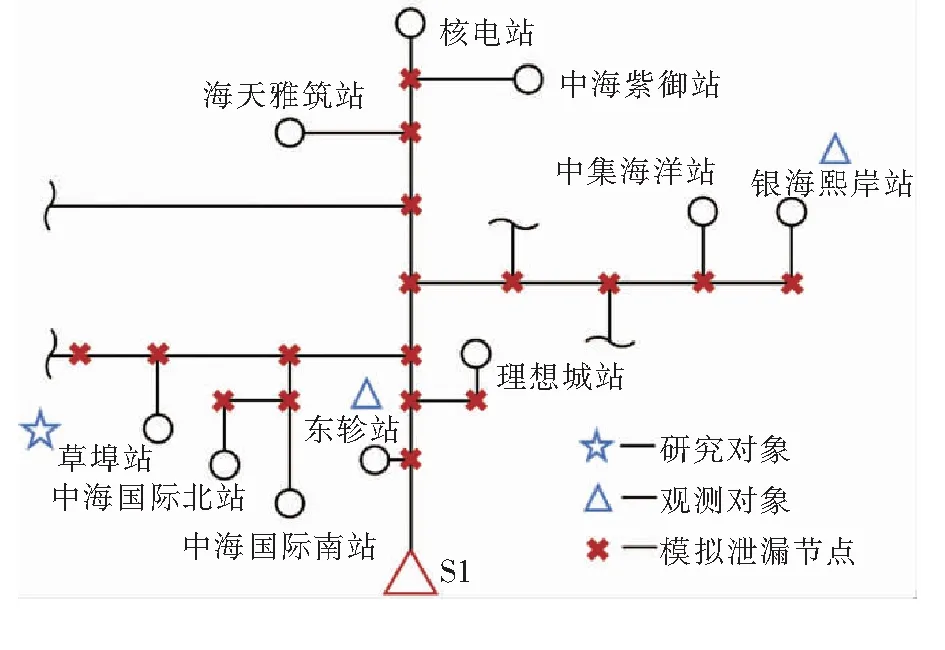
图4 供热管网局部拓扑结构

3.2 数据校正方法应用

将1 994组数据中草埠站供回水压力以及质量流量作为待检测的数据输入孤立森林异常检测模型。异常检测模型参数设置为：样本污染率为10%，子采样规模大小φ为256，iTree数目t为100。根据模型给出的异常分数排序，认为异常数据得分前40位的数据为异常数据。

按照2.1节中的方法构造该管网系统的水力仿真模型，并构造模拟运行数据集，包含热力站局部调节工况数据200组、热源集中调节工况数据60组、泄漏故障工况数据187组、测量异常工况数据30组，作为BP神经网络的训练数据集。基于BP神经网络的异常数据分类模型中神经网络结构设计与参数设置为：5层(含3隐层)神经网络，各层节点数为9、10、10、5、1，学习率η变化范围0.000 1～0.01，最高迭代次数为200。对孤立森林模型识别出的40组异常数据，补充加入对应的东轸站和银海熙岸站对应供回水压力和质量流量，计算各参数变化率，构成测试数据集输入训练好的模型。草埠站及观测站运行数据异常分类后部分分类结果见表3。经人工核验，模型总体分类正确率达92.8%。

表3 草埠站及观测站运行数据异常检测后部分分类结果

异常数据的替换基于数据在时间序列上的关联性，剔除异常值后，采用异常检测结果为正常的数据序列中前后各5个时刻的均值填充该时刻的数据记录(包括供回水压力和质量流量等所有属性)。表4中异常分类结果为4的数据为管网原始数据，其他异常分类结果的数据均为人工添加的异常数据。因此草埠站运行数据发生了测量异常。数据记录进行异常替换部分结果见表4。