基于集成神经网络的水泥生产能耗建模
2020-11-18丁孝华
黄 堃,杨 文,丁孝华
(国电南瑞科技股份有限公司,江苏 南京 211106)
0 引 言
目前,水泥生产作为我国国民经济发展不可或缺的支柱产业,同时作为高能耗产业,水泥生产工艺流程的优化与节能环保的需求日益突出。而对水泥生产的能耗预测是减少电能消耗与污染物排放、提高水泥生产过程的品质和效率的前提条件[1-3]。国内外研究人员对构建水泥炉窑的能耗预测模型进行了研究,一般可分为基于机理建模和基于数据建模2类[4-5],但水泥炉窑煅烧涉及众多环节与设备,参数具有变量多、关联性强等特点。机理建模无法准确描述烧成系统主要参数与能耗的关系。因此数据建模是当前的主流研究方向,其主要是采用专家系统、自适应回归、模糊系统、人工神经网络等人工智能方法对水泥炉窑的能耗建模进行研究[6-8]。
马尔科夫过程常被用于船舶交通流量、瓦斯浓度、需水量、股票走势的预测。吕鹏飞等[9]利用BP神经网络建立船舶交通量的预测模型,预测时结合马尔科夫修正法有效提高了预测精度。韩婷婷等[10]采用马尔科夫修正法修正灰色神经网络模型预测值,使预测的瓦斯浓度变化趋势更贴近实际瓦斯浓度的变化曲线。景亚平等[11]结合马尔科夫修正法建立了灰色神经网络的城市需水量预测模型,试验表明其获得了优于单一灰色神经网络预测模型的预测效果。WANG等[12]建立了基于马尔科夫过程的模糊神经网络预测模型,较精准地预测了股票指数的走势。
相关学者通常采用单个神经网络建立水泥生产窑的能耗预测模型。为提高预测模型的精度,本文在数据预处理时采用平均影响值法筛选能耗敏感变量。建模时以RBF神经网络为元学习器,结合集成算法的思想,建立精度较单个神经网络更高的集成能耗模型。在基于集成模型预测能耗时采用马尔科夫修正法,即依据历史能耗预测值与实际值的残差修正网络输出的能耗预测值,从而提高水泥生产的能耗预测精度。
1 水泥生产的工艺流程
水泥的生产过程主要包含生料制备、熟料煅烧和水泥磨粉3个阶段[13-14](简称“两磨一烧”),其主要生产过程如图1所示。
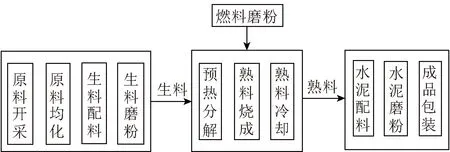
图1 水泥的生产过程Fig.1 Cement production process
水泥生料制备所用原材料包括石灰石、砂岩、黏土、铁矿石、粉煤灰及煤碳等,其中石灰石是水泥生产的主要原材料,具有颗粒较大、硬度较高等特点,需经破碎机破碎处理,实现原料的均化;再将原料按一定比例混合,实现生料的调配;最后经生料磨冲击磨粉的方式处理成细颗粒。
熟料煅烧是水泥生产中能耗最大的阶段,主要包括预热分解、烧成和熟料冷却3个部分。将生料输送至预热器顶端的进料口,生料在预热器内进行预热和少量的预分解处理,而后在预热器下端的分解炉内热分解大部分生料,经过分解的生料进入回转窑,在烧成反应下生成熟料,最后将熟料导入冷却机冷却。水泥磨粉阶段,在刚出冷却机的熟料内加入适量的石膏和矿渣,经水泥磨磨成细粉状的水泥出厂。
综上,水泥烧成系统能耗可能的依赖变量主要包括:喂煤量、CO体积分数、生料流量、冷却剂鼓风管道压力、入冷却机空气温度、熟料流量、预热器的出口压力、预热器废水温度、冷却机出口熟料量、冷却机出口熟料温度、冷却剂烟筒压力、冷却剂烟筒废气温度、分解炉中段表面温度、回转炉中段表面温度和环境温度等。
2 水泥生产能耗预测模型
2.1 数据预处理
从水泥窑分散控制系统(distributed control system,DCS)中按时间序列收集喂煤量、CO体积分数、生料流量、冷却剂鼓风管道压力、入冷却机空气温度、熟料流量等变量值及对应电能消耗的实际数据,作为试验样本数据集。
在利用神经网络进行能耗建模前,不能明确各输入变量对输出能耗结果的影响程度,选择的变量较多时,影响较小的变量会使模型结构更复杂,甚至可能会降低能耗模型的精度。因此需通过合适的预处理方法筛选自变量,获得对能耗输出影响较大的变量作为神经网络的输入变量,本文选用平均影响值法选择参数[15]。其具体实现步骤如下:
若原始训练数据集含有一定数量的样本,每个样本包含n个属性,即样本集P={P1,P2,…,Pn},输出为一个变量Y=[y1,y2,…,ym]。
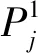
Step3:对所有的输出差值IVj求和并取平均值,得到第j个输入变量的平均影响值 MIVj,本文输出结果仅包含能耗值一项,所以IVj=MIVj。该值的正负号表示该输入变量与输出变量的相关方向,该输入变量对输出变量的影响程度由其绝对值大小表示。
Step4:对MIVj的绝对值按照降序排列,若排序后的前k个平均影响值MIV绝对值的累计贡献率满足
(1)
选择对应的k个输入变量代表全部输入变量重新构建神经网络建模,其中取η0=85%。
2.2 集成能耗模型
在建模阶段,以RBF神经网络为元学习器,结合集成算法的思想,集成学习本质是使用多个元学习器并行学习,并按照某种规则将多个学习结果进行组合,获得一个强学习器,建立比单个模型精度更高的集成模型。神经网络的集成学习算法由个体生成和结论组合2个步骤完成。集成学习算法用于回归建模问题时,结论组合阶段通常将各神经网络的输出经平均或加权平均处理后作为集成模型的输出。个体学习器的数目和集成的效果无关,且个体分类器数量多会增加计算量,占用更多的计算机资源。因此选择差异度大的个体神经网络作为个体生成阶段的重要内容。本文采用差异化训练样本的方式完成个体的生成,具体运行流程为
Step1:将预处理后的试验样本按时间段随机分为T份(时间段间可交叉重叠)。
Step2:对每份样本分别划分训练集和测试集,并分别训练T个RBF神经网络,训练完成后得到T个能够反映不同能耗特征的能耗模型。
Step3:分别用T个模型对同一测试集测试得到T个网络输出结果,对T个结果采用求平均值的方式得出最终的集成输出结果。
集成神经网络建立能耗模型的过程如图2所示。
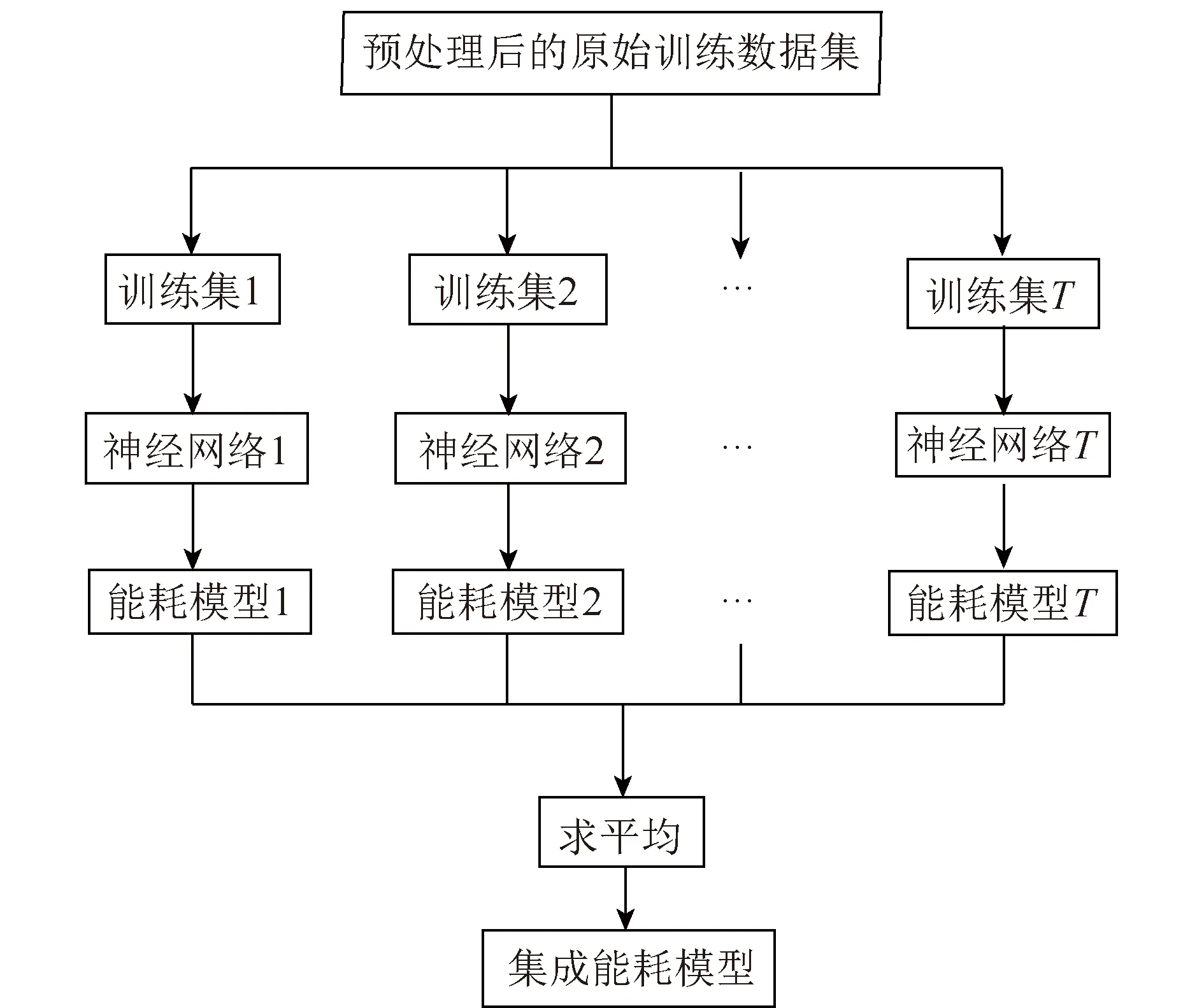
图2 集成神经网络建立能耗模型的过程示意Fig.2 Schematic diagram of the process of integrating neural networks to build energy consumption models
元学习器(RBF神经网络)结构与学习过程如下:
RBF(Radial basis function)神经网络,又称径向基神经网络,是一种包括输入层、单隐层、输出层[16]的3层神经网络。输入空间经非线性变换到隐藏层空间,而隐层空间经线性变换到输出层空间,其结构具体如图3所示。
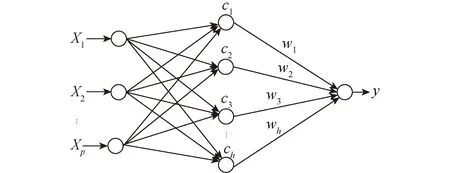
图3 RBF神经网络结构Fig.3 Diagram of RBF neural network structure
RBF网络的基本思想是以RBF作为隐单元的基,从而构成隐层空间,将输入矢量直接映射到隐空间,输入层和隐藏层之间不需要对信号进行处理,只起到信号传递的作用,没有通过权连接。这种映射关系在RBF的中心点确定后即可确定。隐层到输出层通过权连接,即网络输出对可调参数权值而言是线性的。网络的权可由梯度下降法修正获得,RBF神经网络学习速度快且无局部极小问题。理论上隐藏层节点数即中心点越多,RBF神经网络的函数逼近性能越好。
采用高斯函数作为径向基神经网络隐藏层的激活函数,即
(2)
其中,X为p个维度为h的输入向量;h为隐藏层中心点个数;βj为隐藏层的中心宽度;cj为第j个径向基函数的中心点。‖X-cj‖2表示向量X-cj的欧几里德范数平方,即为输入样本点与中心点的距离,当X到cj的距离达到最近时,‖X-cj‖2最小,R(X-cj)达到极大,此时函数被激活,神经网络的输出为
(3)
式中,y为输出单元;b为隐藏层和输出层之间的偏置;wj为隐藏层到输出层的权值。
RBF神经网络的训练包括非监督学习和监督学习2个阶段。在非监督学习阶段使用K-means聚类算法确定RBF的中心点。具体训练过程为
Step1:从输入样本集中随机选取N个样本作为初始的中心点,即c1,c2,c3,…,cN。
Step2:计算每一个输入样本与这N个中心点的欧式距离,即
dj=‖X-cj‖,j=1,2,3,4,…,N。
(4)
Step3:将每个样本点依次划分到与其距离dj最近的中心点所在的簇中。
Step4:计算各个簇中的样本点均值,并将均值作为各簇新的中心点。
Step5:重复Step2~4,直至中心点不再有明显变化,即达到训练要求。
上述训练完成后,各中心点的位置即被确定。
在监督学习阶段使用梯度下降法修正隐藏层与输出层间的权重。具体训练过程为
Step1:初始化权值,并设定的准确率限值ε。
Step2:计算神经网络输出值,并求出误差目标函数值E,即
(5)
其中,p为输入训练样本的个数;ei为第i个样本输入后产生的误差量。为使总误差函数E达到最小值,权重的修正量应与其负梯度值成正比。
(6)
其中,G为高斯函数。更新权值wk+1=wk+Δw,然后转向Step2。
上述训练完成后,权值即可确定。RBF神经网络的训练过程如图4所示。
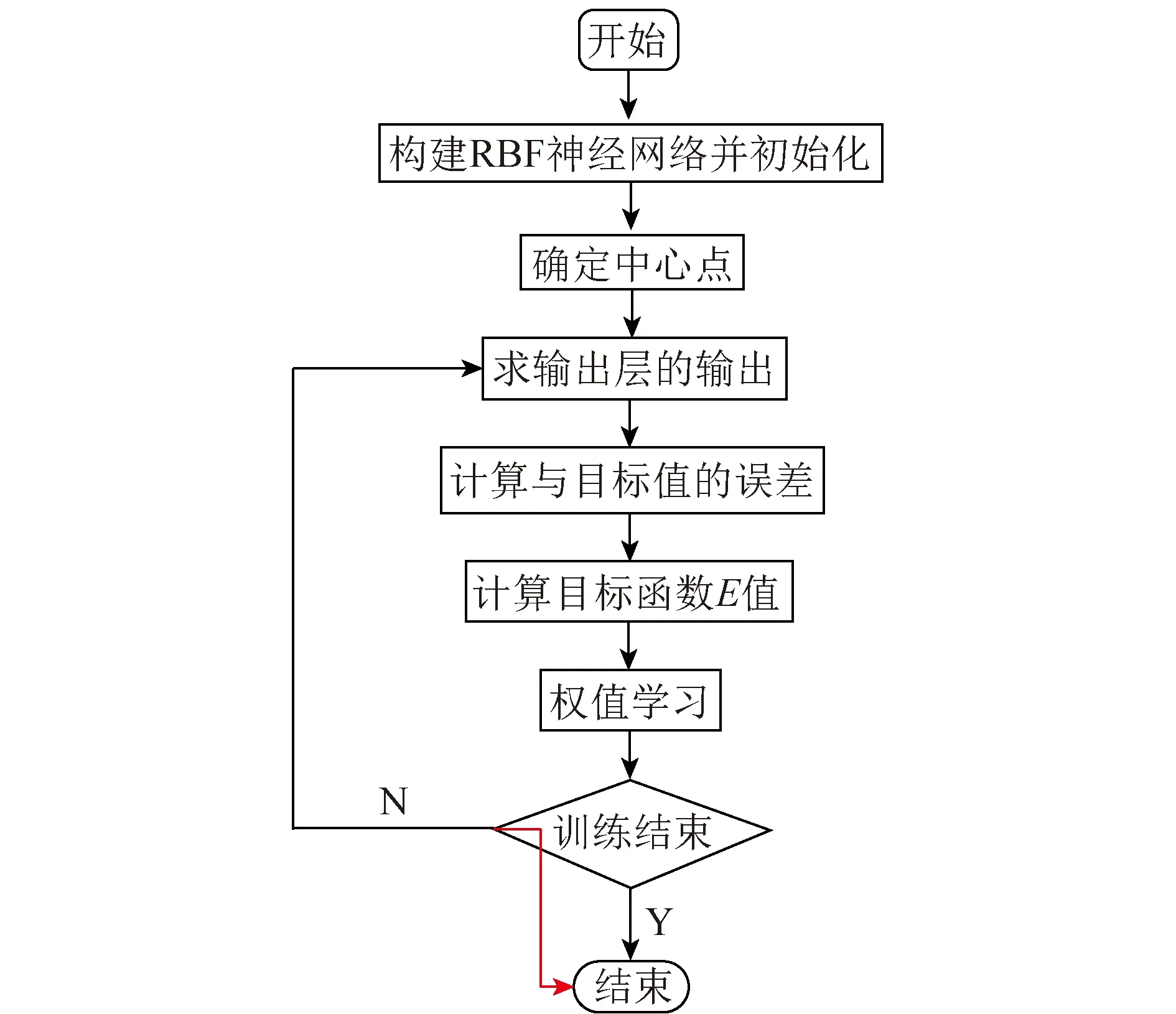
图4 RBF神经网络的训练过程流程Fig.4 Flow chart of the training process of RBF neural network
2.3 预测值的马尔科夫修正
马尔科夫链预测过程描述的是一个随机时间序列的动态变化过程,该过程指在已知t0时刻状态的情况下,系统或者过程在t(t>t0)时刻所处状态的条件分布仅由时刻t0的状态决定,而与t0之前的状态无关[9-10]。马尔科夫过程的处理对象是随机波动性大的离散事件数据,可用数学形式表示为
P{Xk+1=ik|X1=i1,X2=i2,…,Xk=ik}
=P{Xk+1=ik+1|Xk=ik},
(7)
式中,P为条件概率;Xk为子事件;ik为Xk对应的状态。
水泥生产过程的能耗值经采样后得到的是一组按时间序列的离散数据,本文求出测试样本集中的各样本能耗实际值Y1与网络输出预测值Y2的相对残差值,用马尔科夫过程建立残差修正模型,对集成模型输出的能耗预测值修正,使当前预测值更接近真实值。其具体过程为
Step1:按时间序列将测试样本集中的各样本能耗实际值Y1与网络输出预测值Y2比较,求出两者的相对残差Z为
(8)
其中网络输出预测值Y2为4个能耗模型输出的均值。将相对残差值归一化为
中国特色社会主义理论体系的内涵是随着改革与发展的推进而不断深化和丰富的。十八大报告指出“中国特色社会主义理论体系,就是包括邓小平理论、‘三个代表’重要思想、科学发展观在内的科学理论体系,是对马克思列宁主义、毛泽东思想的坚持和发展。”[1]
(9)
式中,Zmin为序列中相对残差的最小值;Zmax为序列中相对残差的最大值;Z*为归一化结果。
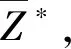
(10)
其中,Δ为黄金分割率0.618;s为任意整数;n为所划分的区间个数。将相对残差值按大小划分出n个状态E1,E2,E3,…,En。n个状态对应的残差区间为
Qi∈(a,b),i=1,2,…,n。
(11)
Step3:求出状态Ei只经1步转移到特定状态Ej的概率,即
(12)
其中,mij为序列中状态Ei转移到状态Ej的次数。1步状态转移概率矩阵由Pij组合形成,即
(13)
根据C-K方程求出k步状态转移概率矩阵为
(14)
Step4:建立马尔科夫链预测模型为
pk+1=p0Ak,
(15)
其中,p0为初始时刻的概率分布;pk+1为k+1时刻的概率分布。由k+1时刻的概率分布可得该时刻对应的状态和残差区间Q∈(Q1,Q2),并根据式(16)修正模型预测值。
(16)
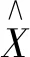
马尔科夫修正法修正能耗预测值的过程如图5所示。
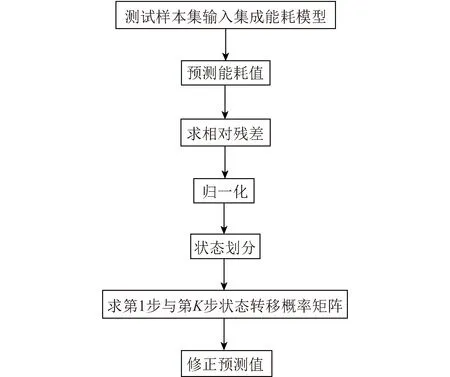
图5 马尔科夫修正法修正能耗预测值的过程示意Fig.5 Schematic diagram of the process of Markov correction method to correct energy consumption forecast
3 实例验证及数据分析
3.1 数据预处理
为了建立水泥生产的集成能耗模型,需要大量的水泥生产过程中的样本数据用于模型训练,因此根据要求在某水泥厂生产现场以5 h作为每组数据的采样间隔,从水泥窑分散控制系统(distributed control system,DCS)中随机收集4个时间段的(时间段可交叉重叠)喂煤量、CO体积分数、生料流量、冷却剂鼓风管道压力、入冷却机空气温度、熟料流量等变量值及对应电能消耗的实际数据,共采集2 100个实测数据组,作为试验样本数据集,按2.1节平均影响值算法步骤进行变量筛选,各变量参数及其 MIV 值见表1。

表1 各变量参数及其MIV值Table 1 Variable parameters and their MIV values
提取8个对生产能耗影响较大的关键特征参数,包括生料流量、分解炉喂煤量、窑头喂煤量、高温风机转速、EP风机转速、预热器出口压、解炉中段炉内温度、环境温度,将其作为神经网络输入的自变量,电能消耗作为输出的因变量,其中部分数据见表2。
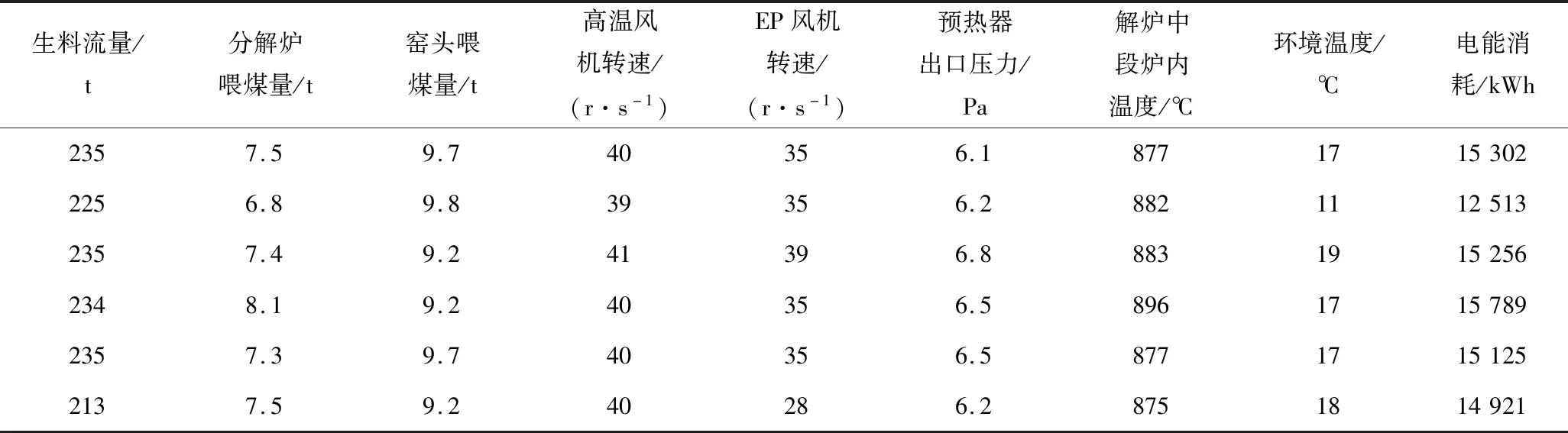
表2 水泥生产过程的部分样本数据Table 2 Partial sample data of cement production process
3.2 集成能耗模型
以Matlab作为试验平台,将2 100个预处理后的数据使用randperm函数打乱顺序,并从中随机抽取100个作为测试集T-train,剩余2 000个数据建立4个训练集T-test,每个包含500个数据样本。 RBF神经网络输入层神的神经元个数设置为8,输出层神经元个数为1。按2.2节RBF非监督学习阶段的K-means聚类算法的步骤,经多次试验后最终确定中心的个数为50个较合适,即可构成8-50-1的神经网络结构。使用newrbe函数创建并训练RBF神经网络,训练完成后得到4个能够反映不同能耗特征的能耗模型,再组合为集成模型。使用sim函数仿真测试,以误差值与决定系数R2作为评价指标。
(17)
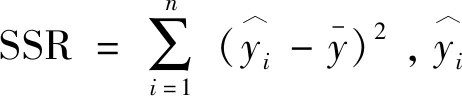
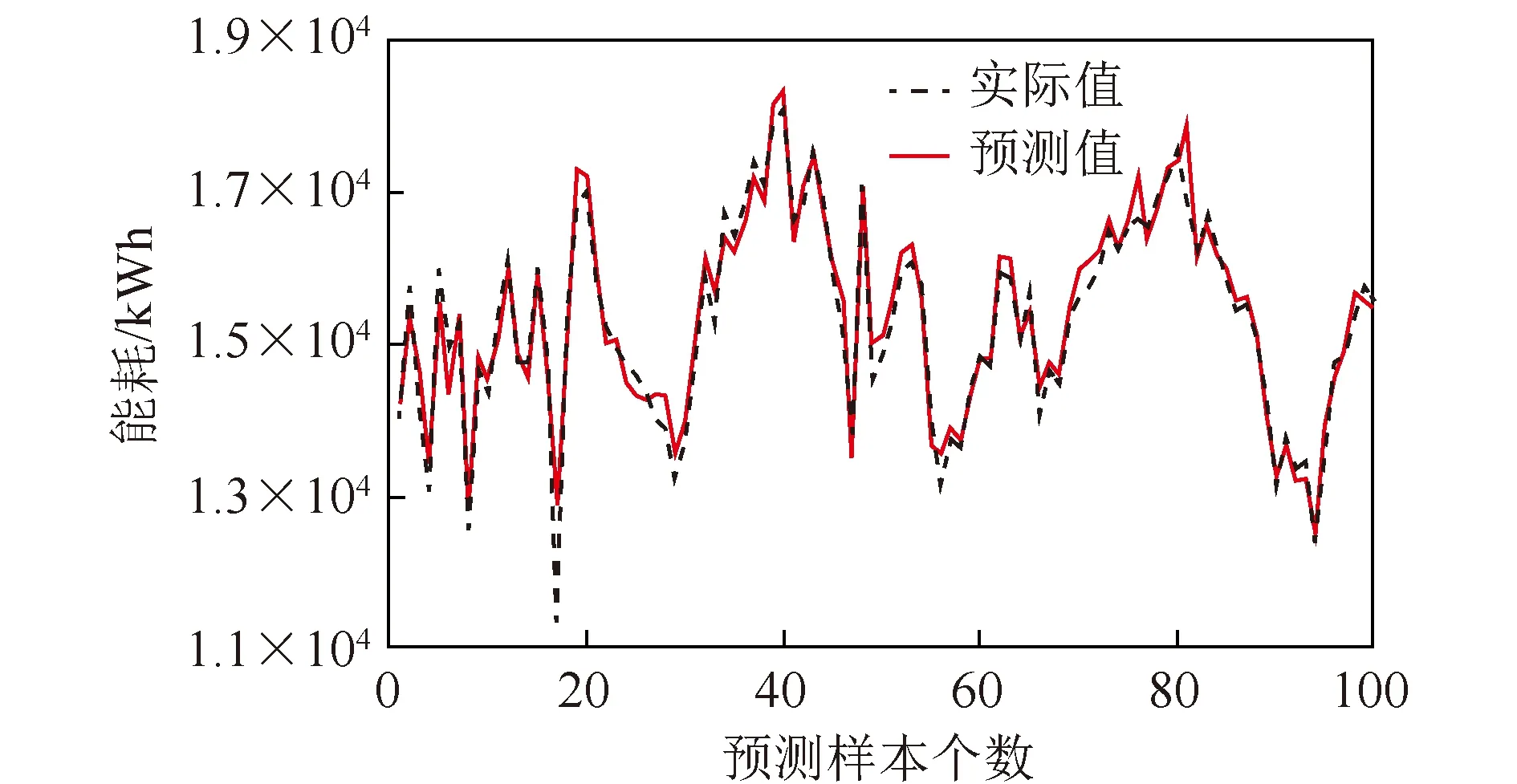
图6 集成模型的能耗预测结果Fig.6 Energy consumption prediction results of the integrated model
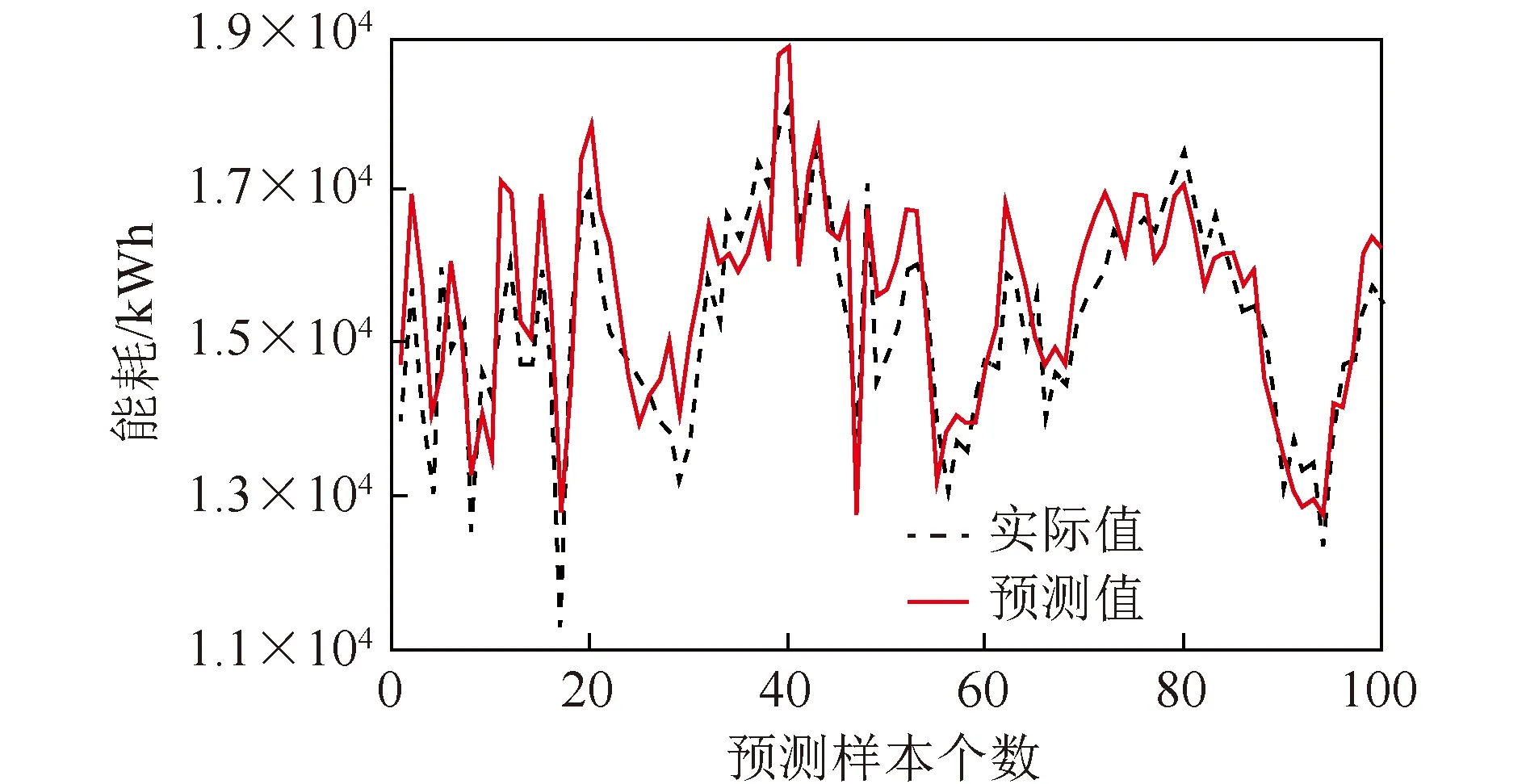
图7 单个RBF神经网络的能耗预测结果Fig.7 Energy consumption prediction results of a single RBF neural network
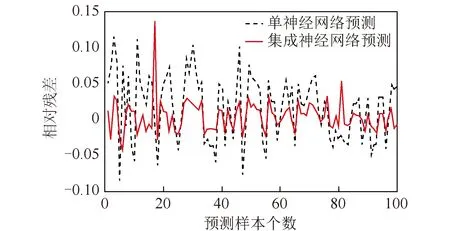
图8 2种方法预测的相对残差对比Fig.8 Comparison of relative residuals predicted by the two methods
仿真结果表明,集成模型的R2=0.924 93,单个神经网络的R2为0.906,集成模型有更高的R2值,说明模型解释性更好。
根据图7两种方法能耗预测与实际值相对残差的比较,定义相对残差均值为
(18)
其中,Zi为第i个样本输入后产生的相对残差值,i=1,2,…,100。计算得到单神经网络预测E=0.043,集成模型预测E=0.016,即集成模型的预测误差的损失函数值更小,模型预测精度更高。
3.3 预测值的马尔科夫修正
为提高预测精度,按时间序列求出测试样本集中的各样本能耗实际值与网络输出预测值的相对残差值(表3),并归一化至[0,1.00](表2的第5列),求出归一后的相对残差的平均值为0.55。根据黄金分割法(取s=1)的规则,将能耗值划分为3个状态E1、E2、E3,E1区间为[0,0.47) ,E2区间为[0.47,0.72],E3的区间为(0.72,1.00]。根据马尔科夫修正过程的描述,第14个能耗值经1步转移到第15个能耗值的1步状态转移概率矩阵为
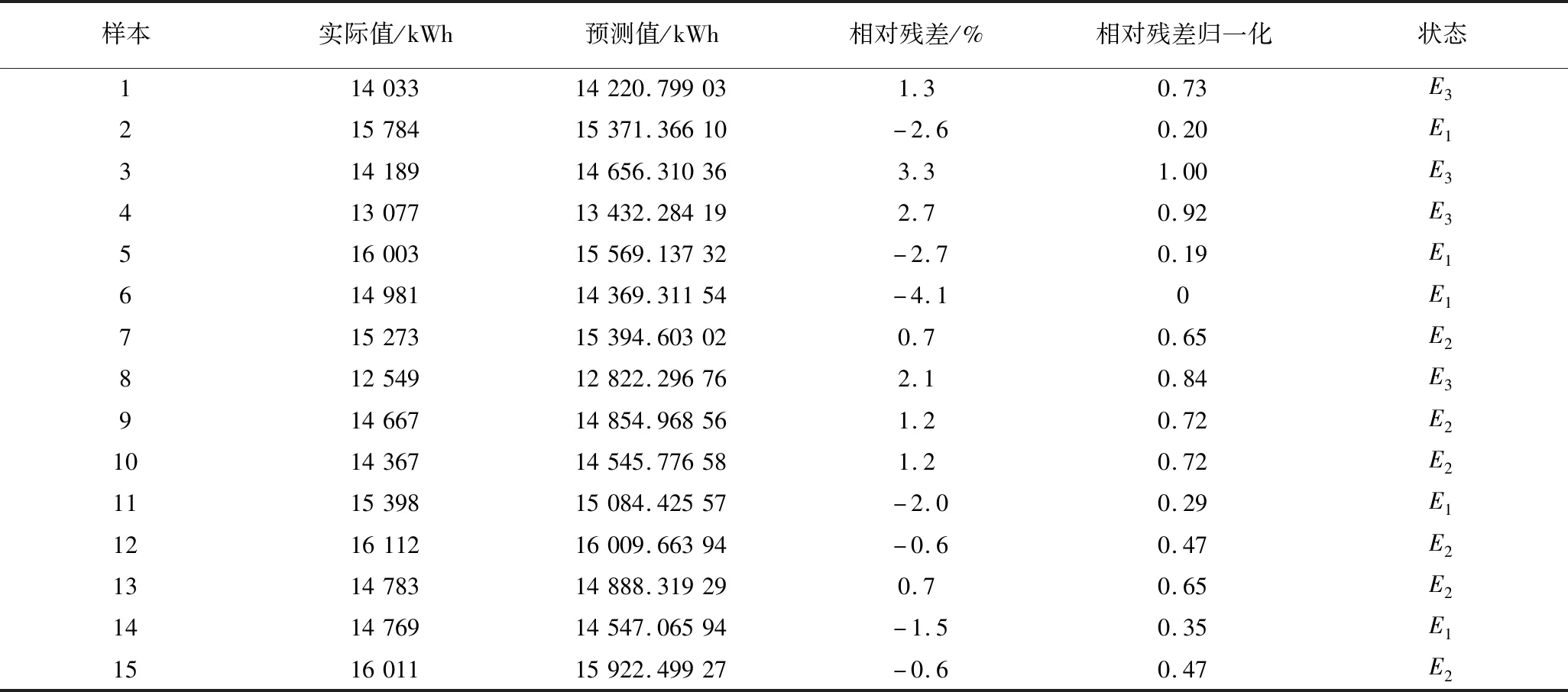
表3 集成模型的能耗预测结果Table 3 Energy consumption prediction results of the integrated model
第13个能耗值经2步转移到第15个能耗值的2步状态转移概率矩阵为
同理可求出k步状态转移概率矩阵。
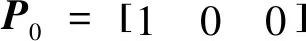
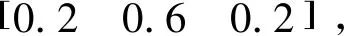
则第15个能耗值处于状态E2的概率较大,并对集成能耗模型的预测值进行马尔科夫修正。
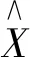
4 结 论
1)在利用神经网络进行能耗建模前,采用平均影响值算法明确各输入变量对输出能耗结果的影响程度,并从12个变量中剔除对网络输出影响较小的6个,使神经网络模型的结构更为简单。
2)在建模中引入集成算法的思想后决定系数R2提高了0.019,预测值与真实值的相对残差均值减少了0.027,说明能耗模型具有了更好的解释性与更高的预测精度。
3)集成能耗模型预测的能耗值经马尔科夫修正后的相对残差从-0.6%降至-0.25%,说明经马尔科夫修正后的水泥生产的能耗预测值更接近实际能耗值。
