基于改进的ELM黄河流域含沙量预测方法研究
2020-11-18杜付然王改堂
□杜付然 王改堂
(1.河南省水文水资源局;2.西安现代控制技术研究所)
0 前言
黄河流域起源于青海,流经四川、甘肃、宁夏、内蒙古、陕西、山西、河南、山东等省市自治区,是我国西北地区和华北地区的重要水源,虽然黄河流域仅占全国2%的径流量,但却肩负着0.15 亿hm2耕地和50 多座大中型城市约1.40 亿人口的供水任务。近年来,随着自然生态环境的破坏,以及流域内在地貌、地形、地质、土壤、植被等方面具有的复杂特性,黄河流域正面临着水资源短缺,且水资源供需矛盾也在日趋尖锐。如何合理有效的利用水资源已成为社会关注的热点问题。黄河流域水文模型的建立不仅在水利工程、水旱灾害防治以及水资源调度、规划和管理等方面具有重要的意义,而且是作为研究黄河问题的一个重要工具和手段。
极限学习机(Extreme Learning Machine,ELM)是由黄广斌教授于2004年提出的一种新的单隐层前向人工神经网络。与传统的BP神经网络相比,在网络学习过程中,极限学习机算法无需调整任何学习参数(如输入权值和阈值),只需通过隐含层输出矩阵的广义逆矩阵即可计算输出层权值,极大地提高了网络的学习速度。由于ELM算法具有学习效率高和泛化能力强等优点,因此被广泛应用于分类,模式识别等领域。然而,在解决实际的工程问题时,样本数据之间可能存在复共线性关系等现象,使用最小二乘法或MP广义逆求解输出权值时易导致病态解问题。针对该问题,王改堂等提出了极限学习机岭回归学习算法(ELMRR),该算法虽然在训练时间和测试时间上均大于ELM 所用的时间,但其测试的性能明显优于ELM。为提高ELM 算法的学习性能,国内外研究学者提出了多隐含输出矩阵的极限学习机算法(M-ELM),融合极限学习机(PELM),增量型极限学习机改进算法(I-ELM),经验模式分解极限学习机(EMD-ELM),多元时序驱动ELM 算法。虽然这些算法取得了良好的效果,但大都是从结构形式上做了更改,没有从算法的本质入手,为此,文章将特征加权核函数应用于极限学习机学习算法中,提出了特征加权核极限学习机算法(Feature Weighted Kernel ELM,FWKELM)。通过该方法预测黄河流域的含沙量,实验结果验证了该方法的准确性、有效性。
1 极限学习机
假设ELM 网络的隐含层节点数为L,激活函数为g(x),对任意Q个不同的样本(xi,yi)∈Rn×Rm,ELM网络的输出与实际数据之间实现零误差逼近,则存在εi,wi,bi有:

式(1)简化为:

式中,

式中,wi=[wi1,wi2,…,win]T为隐含层的第i 个节点与输入层之间的连接权值,其值为0~1之间的随机数;εi=[εi1,εi2,…,εim]T为隐含层的第i 个节点与输出层之间的连接权值;bi代表隐含层i节点的阈值。H为隐含层输出矩阵,则ELM网络的输出权值ε的最小二乘解为:

式中,H+为矩阵H的Moore-Penrose广义逆。
2 改进算法
2.1 激活函数
激活函数是ELM 算法的核心,激活函数选择的好坏直接影响网络的非线性映射能力和学习精度。径向基函数(RBF)是一个取值仅仅依赖于离原点距离的实值函数,由于该函数具有学习收敛速度快、非线性映射能力强等特点,因此,文章选择径向基函数(RBF)为例进行分析。
RBF函数可表示为:


2.2 特征加权矩阵
不管是分类算法还是回归算法,对当前任务的分析并不是所有的特征做出同等贡献,因此,我们需要根据特征的贡献程度来选择不同的权值。特征加权矩阵的出现不仅可以避免被一些弱相关或不相关的特征所支配,而且能使特征空间中点与点之间的位置发生改变,从而寻找最好的线性超平面来提高算法的性能。文章采用自助特征加权(Bootstrap feature weights)分析方法来计算权值,具体的算法过程如下:
假设自助特征加权算法的随机样本为X ={X1,…,Xn}⊂RP,Xj=(xj1,…,xjp)为第j个样本,则样本的标准偏差可表示为:

构件设计主要是应用了草图设计和线框建模等功能,以此进行工程结构的三维构件设计。其中,构件装配主要是指对于设计好的构件模型,要装配成一个工程结构模型,从而促进装配工作的顺利完成,而结构配筋主要是指在设计好的构件上进行配筋工作,这与以往配筋图纸存在极大的区别。在该模块中,对全三维的钢筋配置进行了广泛应用,设计人员在施工之前,可以充分了解施工时的真实效果。此外,地质建模主要是指通过钻探和物探等方式获取的勘察资料,借助三维建模技术,及时构造出三维地质模型。

第k个特征变量的权值wk为:

步骤1:选择B 个独立的Bootstrap 样本Xb={Xb1,…,Xbn},b=1,…,B,其中Xbj=(xbj1,…,xbjp)是从X={X1,…,Xn}中有放回抽取的样本。
步骤3:计算B次复制样本的均值估计特征权值wk为:

步骤4:特征加权矩阵P为:

2.3 特征加权激活函数
定义1:令K是定义在X×X上的核函数,X⊆RP,P是给定输入空间的p阶线性变换矩阵,其中p是输入空间的维数。定义为

式中,P为特征加权矩阵。
由式(12)可以得到,特征加权径向基函数为:
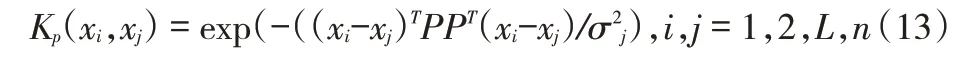
式中,xi是第i 个样本数据的输入向量,xj为高斯函数的中心,σj为高斯函数的宽度。
2.4 算法步骤
FWKELM算法步骤如下:
步骤1:选择训练样本数据(xi,yi),其中i=1,2,…n,计算训练样本数据的输入数据矩阵为X,输出数据矩阵为y;步骤2:根据特征加权算法步骤计算或构造特征加权矩阵P;步骤3:选取式(13)作为改进算法的激活函数;步骤4:随机产生输入权值wi和阀值bi;步骤5:采用式(3)计算隐含层输出矩阵H;步骤6:采用式(5)计算输出权值ε。
3 黄河流域含沙量预测
为了验证该算法的有效性和可行性,文章以龙门(马王庙二)站为例对黄河流域含沙量(kg/m3)进行预测,选择水位(m)、起点距(m)、水深(m)、测点深(m)、流速(m/s)和水温(℃)作为黄河流域含沙量的影响因子,利用文章提出的FWKELM 算法对黄河流域的含沙量进行预测。
实验共采集了100组样本数据,为了弥补在记录数据时产生的误差,对每组样本数据增加0.01×10-1~0.09×10-1的随机数。实验过程中,首先对样本数进行归一化处理,然后将归一化处理后的样本数据随机选取50 组数据作为训练样本,剩余的50组数据作为测试样本,实验采用均方根误差(RMSE)作为评估算法的性能指标。图1给出了FWKELM 算法的预测值与误差,图2 给出了ELM 的预测结果与误差。FWKELM 和ELM算法的性能比较如表1所示。
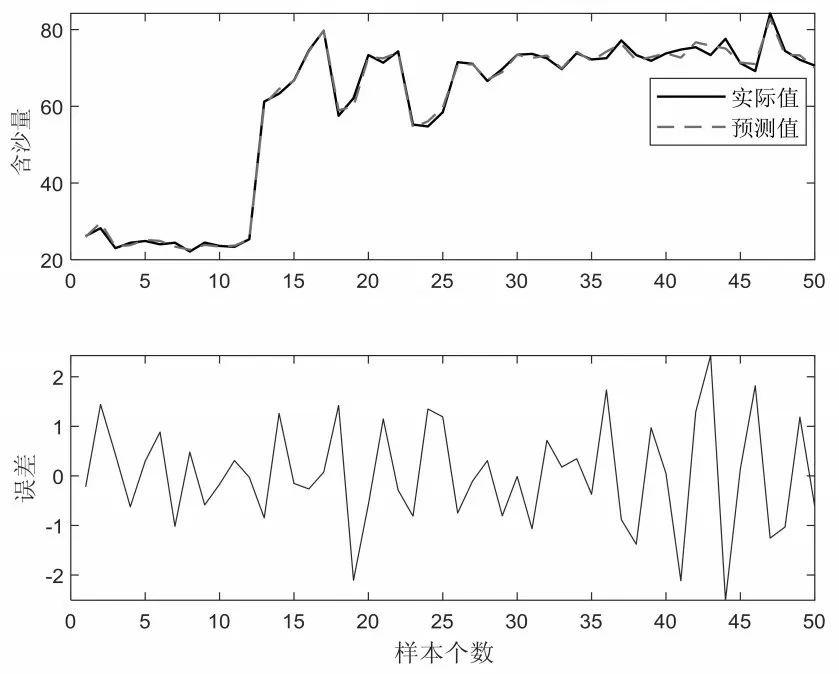
图1 FWKELM算法的预测结果与误差图
从图1、图2和表1中可以看出,FWKELM算法对黄河流域含沙量的预测精度优于ELM 算法,FWKELM 的测试误差大多数情况处于[-2,2]之间,仅有个别点的预测误差的绝对值>2,而ELM算法的预测误差明显不如FWKELM算法的测试结果。
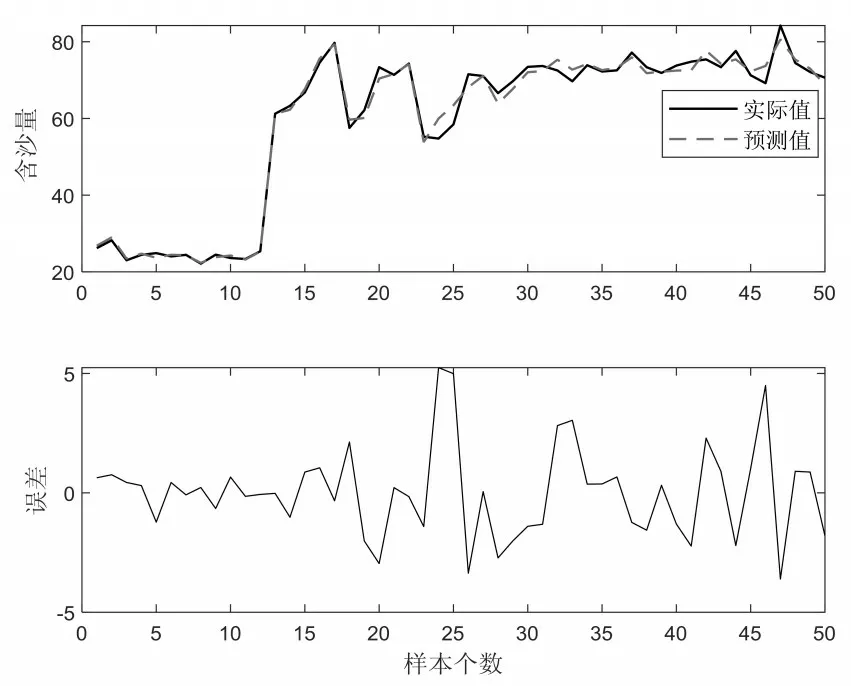
图2 ELM算法的预测结果与误差图
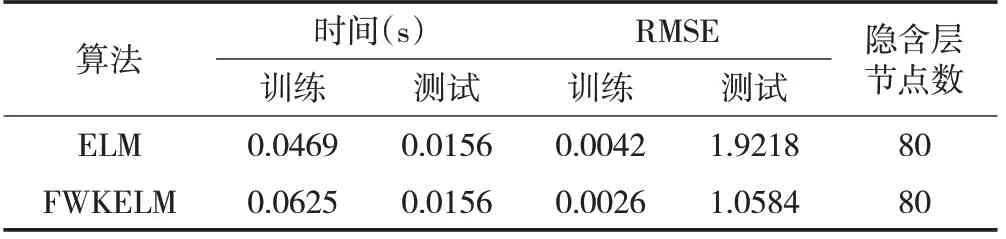
表1 FWKELM和ELM算法结果比较表
4 结论
文章针对极限学习机(ELM)仅考虑样本重要性的问题,提出了一种改进的ELM学习算法——基于特征加权核函数的极限学习机算法。该算法从样本的特征重要性出发,使用自助特征加权算法对其激活函数进行了加权处理。通过对黄河流域含沙量的预测结果表明,文章所提出的算法具有较好的预测精度和泛化性能。
