减少弃水的风-光-梯级水电站双层优化模型

许欣慧， 舒征宇， 陈 锴， 李世春

（三峡大学 水电站运行与控制湖北省重点实验室， 湖北 宜昌 443002）

0 引言

近年，风能、太阳能等可再生能源得到快速发展，大量可再生能源需要并网消纳，但风电场、光伏电站往往远离负荷中心，位于电网末端，所产生的电能须要与同地区的梯级水电站共用输电通道进行输送[1]～[3]。 然而，电网建设相对滞后于用电需求， 这导致同地区共用有限输电通道的风电、光伏、梯级水电站在汛期的弃水、弃电风险进一步增大。

目前，针对风-光-水联合运行系统的研究主要集中在短期调峰补偿与多能互补性。 文献[4]以雅砻江风光水互补系统为研究对象， 建立了大型风光水互补发电日内优化调度模型， 提高了风光电量的消纳。 文献[5]利用互补系数将分系统评价与联合发电系统评价相结合， 构建了适用于评价风光水日内互补特性的指标框架， 能够对发电系统的互补特性进行准确分析。 文献[6]以风光水系统发电量最大为目标， 建立了人工神经网络模型提取调度规则，提高了互补系统的经济效益。文献[7] 充分考虑风光水发电系统内风光出力的不确定性， 建立了风光水互补发电系统短期调峰优化模型， 进一步提高了互补系统的调峰能力。 文献[8]分析了风、光、水、火多能源介质的时空互补特性，建立了多能源基地联合优化调度模型，进一步促进了可再生能源的消纳。 但这些研究大多集中在互补系统的短期调峰补偿和能源间的互补性，对互补系统的长期优化调度研究较少， 且未考虑有限输电通道对系统外送电量的影响。 基于上述分析，在中长期优化调度中，若风-光-梯级水电站系统在水电汛期出力较大时， 系统出力超过输电断面的极限传输容量（Total Transfer Capability，TTC）而增加了弃电的风险[9]。 将风电场、光伏电站的出力特性和梯级水电站的库容调节紧密结合，全面考虑梯级水电站水量和电力之间的联系、库容与电力补偿的相互制约关系[10]～[13]； 分析断面TTC 对多能源系统外送电量的影响，建立风-光-梯级水电站长期优化调度模型， 成为解决同一地区风-光-梯级水电站系统电力集中外送的必然要求和难点问题。

本文研究了风-光-梯级水电站系统因输电断面限制造成的弃水问题。 针对风-光-梯级水电站系统存在汛期出力过大造成弃电的风险， 分析了系统在汛期弃电的原因， 构建了考虑减少弃水的风-光-梯级水电站双层优化模型，通过挖掘梯级水电站的补偿能力， 优化水电各时段的水位和出力，实现长期调度和水电蓄能的联合优化。最后通过算例验证了模型的有效性。

1 梯级水电站弃水分析

由于风-光-梯级水电站系统内各发电站的发电特性不同， 尤其是梯级水电站汛期与非汛期发电差异明显，严重制约着系统电量外送水平。梯级水电站在非汛期发电能力有限， 系统总出力偏低，输电通道利用率也较低；在汛期，系统总出力往往会出现超过断面TTC 的情况，出现弃电的风险。 对于某一输电线路断面，其断面TTC 限制表达式为

式 中：Ph，t，Pw，t，Ps，t分 别 为t 时 段 梯 级 水 电 站 有 功出力、风电场有功出力、光伏电站有功出力；Ns为断面最大传输容量极限。

当系统出力超过断面TTC 时，超出TTC 部分的出力作弃水处理。 系统出力受到断面TTC 限制，在t 时段的弃水出力平均值ΔPh，t为

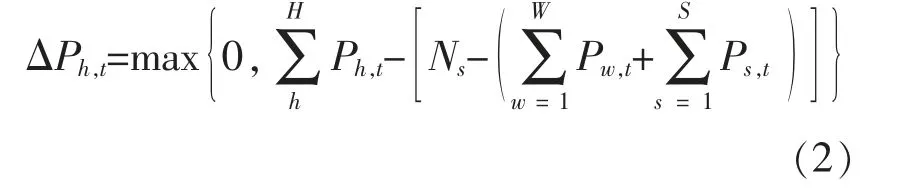
本文弃水电量是指梯级水电站在有发电能力情况下的弃水， 与水电站不满足自身运行约束条件所造成的弃水不同。 为此，将受到断面TTC 限制而弃电前的部分出力称为电站的发电能力。

2 风-光-梯级水电站双层优化模型

风-光-梯级水电站双层优化模型为双层递阶结构，其优化框架图如图1 所示。

图1 双层优化框架图Fig.1 Double-layer optimization framework

由图1 可知，上层为协调优化层，风电场、光伏电站优先利用输电通道进行输电， 梯级水电站根据风、 光电站出力以及径流预测值， 在满足防洪、灌溉、航运等综合利用的前提下，合理调整各时段出力计划， 根据月平均出力计划计算得到月度总电量，通过各月度电量来制定年发电计划；根据日前来水情况以及月度电量计划来协调制定日前出力计划， 通过日前出力计划以及日内实际来水情况及时调整日内出力，实现风-光-梯级水电站发电效益最大化。下层为蓄能优化层，根据汛期梯级水电站弃水的情况， 在满足梯级水电站最小出力限制以及水电站运行约束的前提下， 挖掘梯级各库间的补偿能力， 优化梯级水电站的运行水位，保证梯级水电站蓄能值最优，将汛期梯级水电站的弃水储存在水库中，实现能量的时序转移。

上层协调优化调度的结果作为下层优化水库蓄能的决策依据； 下层梯级水电站不同的蓄能方案将改变梯级水电站出库、 入库流量以及各水库的水位，反馈到上层重新进行优化，循环往复，直至最优。

2.1 上层优化模型

本文假设历史风速服从二参数的威布尔分布，则风电场的出力为

式中：vw为风速；cw为尺度参数；kw为形状参数；为t 时段平均风速；vwi为切入风速；vwo为切出风速；vr为额定风速；Pr为风电机组的额定出力；n为风速-功率系数。

光伏电站的出力与温度和光照相关， 光伏电站出力为

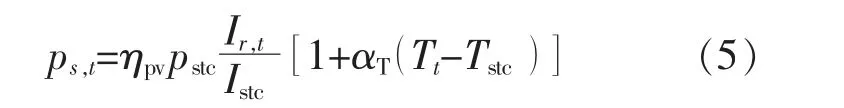
式中：ηpv为光伏机组转化效率；pstc为标准条件下（对应太阳能辐射强度=1 000 W/m2， 温度Tstc=25℃） 光伏出力；αT为功率温度系数；Ir，t为t 时段平均太阳辐射强度；Tt为t 时段平均温度。

2.2 下层优化模型

2.2.1 目标函数

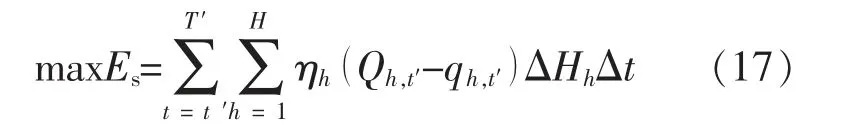
式中：Es为弃电期梯级水电站蓄能值；T′，t′分别为总弃电时段、第t′时段时长；ηh为水电站h 的综合出力系数；Qh，t′为水电站h 在t′时段的入库流量；qh，t′为水电站h 在t′时段的出库流量；ΔHh为水电站h 在t′时段的净水头。

2.2.2 约束条件

①最小出力约束

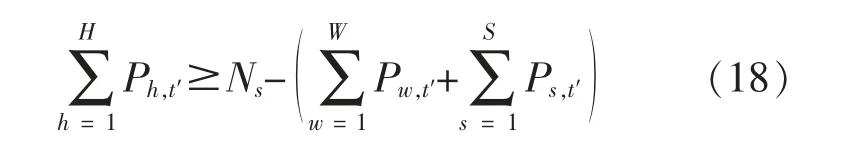
式中：Ph，t′为水电站h 在t′时段出力；Pw，t′，Ps，t′分别为t′时段风电场有功出力、光伏电站有功出力。

②水电站运行约束

水电站运行约束考虑水量平衡约束、 库水位约束、发电流量约束、出力约束、出库流量约束，分别见式（9）～（13）。

2.3 模型求解

含水电优化调度的系统中调度决策变量与状态变量之间呈现隐形与非线性关系。 上层模型采用 逐 步 优 化 算 法[14]（Progressive Optimization Algorithm， POA） 和水位廊道约束耦合方法相结合进行求解，POA 将原问题转化为一系列单时段优化问题。在求解过程中，通过水库水利关系将多约束条件转化合并来确定各时段水位约束廊道，实现高维约束的降维，提高求解效率。在优化过程中，风电、光伏电站优先上网，不直接参加优化搜索，因此风-光-梯级水电站系统的优化过程与梯级水电站优化过程具有一致性。 下层模型采用离散微分动态规划法 （Discrete differential Dynamic programming， DDDP）[15]，将水库水位在水位上、下限间进行离散， 以水位廊道的形式确定水位的上下限，缩小了问题的可行域，在保证求解精度的同时，保证了算法的时效性。 算法求解流程图如图2所示。

图2 算法求解流程图Fig.2 Algorithm solution flow chart

①设定调度期为T，调度时段为t，梯级水电站总数为H，各水电站编号为h（0＜h＜H），决策变量为t 时段各水电站的平均发电流量qh，t，状态变量为t 时段水电站水位Zh，t。 确定各水电站t 时段的初始水位Zh，t，并选定搜索步长与优化终止的计算精度。

②第1，2 时段开始，固定状态变量Zh，1和Zh，3，调整Zh，2。 在满足约束条件下，计算两阶段的决策变量qh，1和qh，2，进而求出两阶段的出力Ph，1和Ph，2，并使得两阶段的出力最大。

③求出与步骤①中两阶段出力最大与之对应的状态变量Zh，2和决策变量qh，1和qh，2。

⑤将新的水位序列作为初始值，重复步骤②～④， 直到满足新水位与之前给定水位之差小于给定精度为止。此时的水位为最优状态变量，求出对应的决策变量。

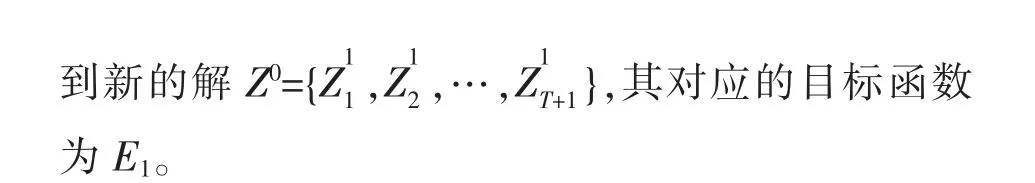
⑧比较E0与E1， 若两者之差小于计算精度ε，则满足收敛条件，将Z1作为最优解输出；否则令Z0=Z1并重复步骤⑦， 将求出的最优水位反馈到上层进行迭代计算，直至满足收敛条件为止。

3 算例分析

3.1 仿真算例

以清江中下游风-光-水清洁能源基地为例，该基地包含一个三级的梯级水电站、 两个风电场、一个光伏电站，风-光-梯级水电站系统打捆送电示意图如图3 所示。 优化调度周期为1 a，控制时段为1 m。 各水电站的基础数据如表1 所示。各水电站的区间来水流量根据以往历史数据获取，初始水位取历史多年平均水位，控制各水电站调度期末水位与初始水位相等，各水电站的运行约束条件均参考2019 年水电站实际运行值。风电场D，E 总装机容量分别为400，300 MW；光伏电站F 的装机容量为200 MW； 线路断面TTC为3 100 MW。

图3 发电系统打捆送电示意图Fig.3 Schematic diagram of bundling and power transmission of power generation system

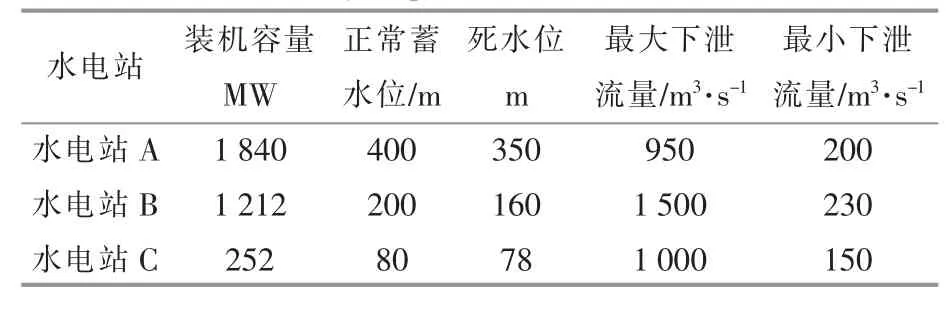
表1 水电站基础数据Table 1 Hydropower station basic data

3.2 结果对比分析

以典型丰水年为例， 各水库天然流量选取为丰水年多年历史入库的平均值。 为验证本文双层优化模型的有效性， 与仅考虑外送电量最大的协调模型调度结果进行对比分析， 协调模型的蓄能值由该模型最终优化结果进行计算得到。 表2 为两种模型的发电情况对比，图4 为风-光-梯级水电站总出力图。

表2 发电情况对比Table 2 Results of Power generation， water abandonment and delivery 亿kW·h

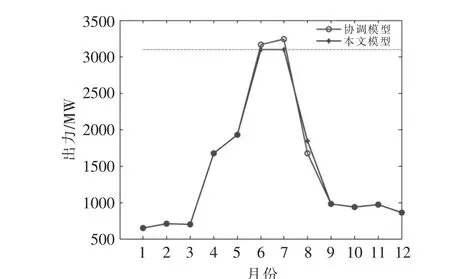
图4 风-光-水系统总出力Fig.4 Wind-light-water system total output

由表2 和图4 可知：与协调模型相比，虽然双层模型的实际发电量减少了0.19 亿kW·h， 但系统外送电量提高了1.28 亿kW·h； 弃电期梯级水电站蓄能值增加了1.4 亿kW·h， 减少了因断面TTC 限制造成梯级水电站的弃水。 双层模型通过挖掘梯级各库间的补偿能力， 将系统出力过大超过断面TTC 限制的电能以水量的形式储存在水库中，实现了电能的时序转移。

风电场、光伏电站的出力如图5 所示。

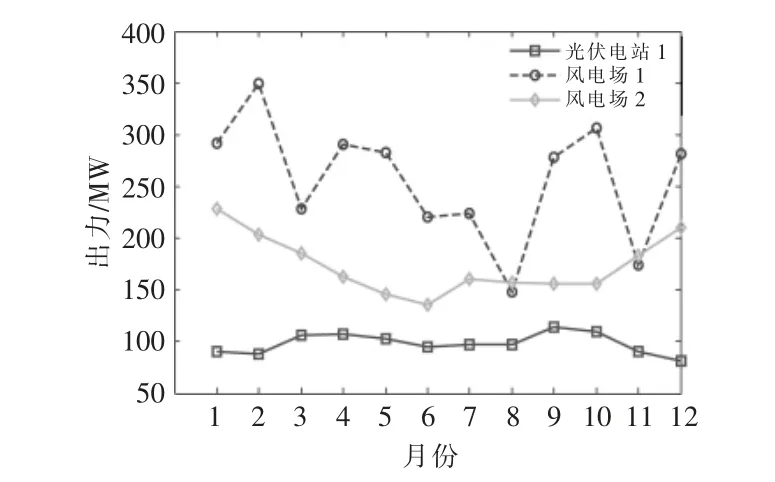
图5 风电场与光伏电站出力Fig.5 Wind farm and photovoltaic power plant output

在保障风电场、 光伏电站所产生的电能优先利用输电通道输送电能后， 梯级水电站利用输电通道的剩余传输容量输送电能， 基于两种调度模型下梯级水电站的出力对比如图6 所示。

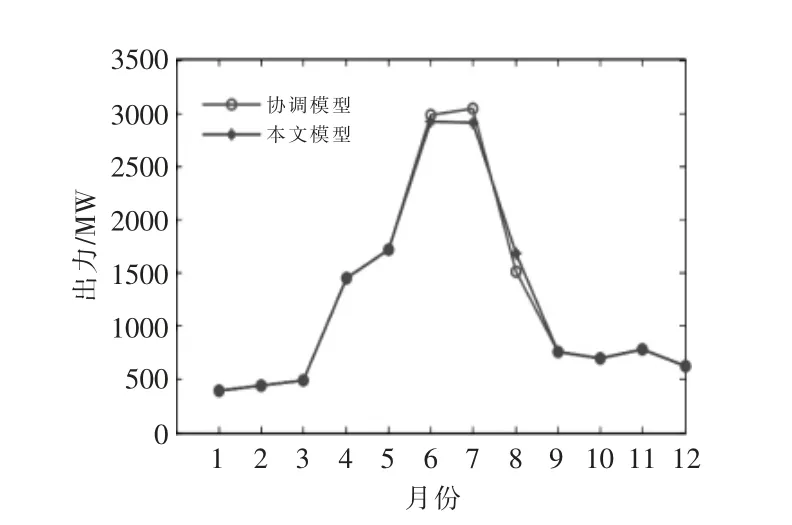
图6 梯级水电站总出力Fig.6 Total output of cascade hydropower stations

由图6 可知：与协调模型相比，双层模型在汛期6，7 月时梯级水电站出力减少； 而在汛期结束后的8 月出力增大， 实现了梯级水电站电能的时间转移， 同时8 月的输电通道利用率由53.9%提升至59.44%。 如图7 所示。

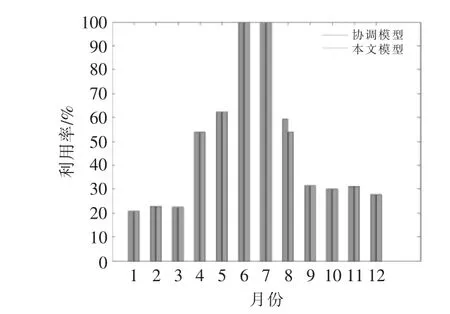
图7 通道利用率对比图Fig.7 Comparison of channel utilization

图8 水电站A 月平均出力Fig.8 Hydropower station A monthly average output month

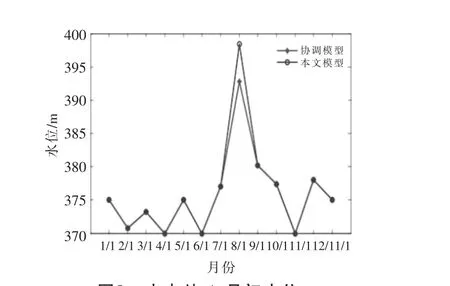
图9 水电站A 月初水位Fig.9 Hydropower station A water level at the beginning of the month

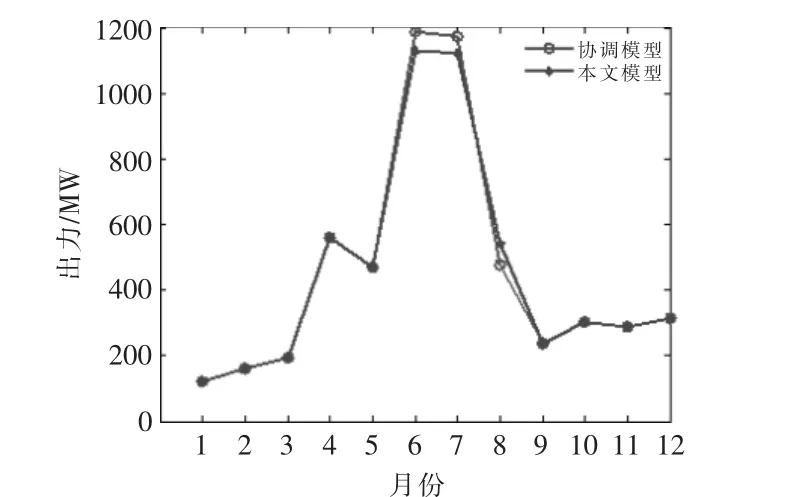
图10 水电站B 月平均出力Fig.10 Hydropower station B monthly average output

图11 水电站B 月初水位Fig.11 Hydropower station B water level at the beginning of the month

图8～11 分别为水电站A 的月平均出力对比图、月初水位对比图，水电站B 的月平均出力对比图、月初水位对比图，其中水电站A 和B 的水位和出力均为各时段的平均值。 水电站C 作为日调节水电站，两种调度模型的调度结果差异不大。

表3～5 分别为水电站A 和B 的蓄能值对比、出力对比、水位对比。

表3 蓄能增量对比表Table 3 Comparison table of incremental energy storage 亿kW·h

表4 出力对比表Table 4 Output comparison table MW

表5 水位对比表Table 5 Water level comparison table m

结合图8～11 和表3～5 可知： 与协调模型相比，双层模型中水电站A 在汛期的7 月份增加蓄能值1.06 亿kW·h，降低出力114 MW，抬高水位5.6 m，8 月份增加出力101 MW；水电站B 在汛期6 月份增加蓄能值0.52 亿kW·h， 降低出力56 MW， 抬高水位7.8 m，7 月份减少蓄值0.18 亿kW·h，降低出力49 MW，抬高水位5.1 m，8 月份增加出力68 MW。相比于7 月份水电站A 和B 的水位，8 月份由于水电站A 入库流量大于发电流量，导致水电站A 的水位升高；水电站B 又因为水电站A 发电流量较大，水电站B 的发电流量小于水电站A 的发电流量，使得水电站B 的水位升高。 双层模型通过调节各水电站的运行水位、入库、出库流量，利用水库库容蓄水，减少梯级水电站在汛期的出力，增加水电蓄能值。 双层模型中，梯级水电站总出力在6，7 月份均有降低， 但由于受到断面TTC 限制，在6，7 月系统的外送电量与协调模型并无差异。

4 结论

本文基于梯级水电站的库容储能特性， 兼顾风-光-梯级水电站系统发电效益以及梯级水电站蓄能效益，建立了减少弃水的风-光-梯级水电站双层优化模型， 充分挖掘梯级水电站的补偿能力，实现电能的时段转移。模型采用逐步优化算法和离散微分动态规划算法进行求解，结果表明：①通过挖掘梯级各库的互补能力， 优化梯级水电站的运行水位，调整各时段梯级水电站的出力，利用库容储能特性将电能从汛期转移到非汛期， 实现水库蓄能并转移发电时段；②将所建立的风-光-梯级水电站双层优化模型应用于清江中下游风光水清洁能源基地，通过典型丰水年的调度计算，梯级水电站减少弃水电量1.28 亿kW·h， 梯级水电站蓄能值增加1.4 亿kW·h，输电通道利用率提高了5.55%， 表明双层模型提高了风-光-梯级水电站系统的经济效益。