基于量子行走的量子秘密共享方案

李雪杨，昌 燕，张仕斌，代金鞘，郑 涛

(成都信息工程大学 网络空间安全学院，四川 成都 610225)

0 引 言

量子秘密共享(QSS)是经典秘密共享和量子理论的结合[1-9]，它使得秘密信息(经典信息或量子编码信息)通过量子操作分发、传输和恢复。QSS的安全性基于量子力学的基本原理，这使得QSS比传统的秘密共享更安全。最早的QSS方案由Hillery等在1999年提出[10]，他们采用(Greenberger-Horne-Zeilinger，GHZ)纠缠态完成了秘密共享。此后，越来越多的基于Bell纠缠态或多粒子纠缠态的QSS方案被提出[11-13]。然而，利用Bell态或多粒子纠缠态的纠缠特性来完成粒子隐形传态，实现秘密共享方案，纠缠态的制备需要消耗较多资源，且在现有技术下不易制备和测量，这些技术障碍使得此类QSS方案的实用性大大降低。对此，郭国平、郭光灿提出一种无纠缠的QSS方案[14]，通过基于密钥的秘密共享完成经典信息的秘密共享，此后，闫凤利等提出一种无纠缠的多方和多方之间的QSS方案[15]，但随后文献[16]指出该方案在粒子传输上存在安全隐患，造成秘密信息泄露，并给出了相应改进措施。此类QSS方案虽然没有采用纠缠态粒子的纠缠特性完成秘密共享，但很难保证粒子传输的安全性。

量子行走的概念最早在1993年被Aharonov等提出[17]，它起初是用于研究量子扩散现象，是经典随机行走的量子模拟。随后，Ambainis等提出了线性量子行走模型[18]，并被Aharonov等提升为图上的量子行走模型[19]。此后，人们提出了许多关于量子行走的研究[20-23]。最近，量子行走已被证明是量子信息处理任务中的一种有前景的资源，它可以用来实现门集，已在许多物理系统中制造。

由于量子行走可以使粒子间产生纠缠关系，我们提出一种不依赖于初始纠缠态粒子制备且更为有效的QSS方案。在我们的方案中，我们采用量子行走系统使得单粒子在量子行走过程中自发产生纠缠，这使得我们的方案不需要制备初始纠缠态粒子，只需要制备单粒子，而单粒子在现有技术下更容易生成和测量。此外，我们利用编码规则将秘密信息编码为量子态，并采用两步量子行走系统完成粒子的隐形传态，确保了粒子在通讯过程中的安全性。

1 基础理论

1.1 线性量子行走

量子行走是以量子作为载体对经典随机行走进行的模拟，它可以根据量子的测不准性来模拟混沌非线性的动态行走行为，建立加密的量子传输通道。

量子行走发生在一个复合的希尔伯特空间中，由两个主要的量子空间组成，分别是位置空间和硬币空间，表示为

H=Hp⊗Hc

(1)

其中，Hp表示位置空间 {n,n∈Z}，Hc表示硬币空间，即量子行走的硬币方向 {|0〉,|1〉}。

量子行走的每个步骤W(l)可以描述为等式

W(l)=E(l)·(I⊗C)

(2)

其中，E(l)=S⊗|0〉〈0|+S†⊗|1〉〈1|，S为移位运算符，S=∑n|n+1〉〈n|，I是Pauli操作符σI，C是硬币操作符，当硬币操作符为 |0〉 态时，它使硬币粒子从 |n〉 态移动到 |n+1〉 态，当硬币操作符为 |1〉 态时，它使得硬币粒子向后移动到 |n-1〉 态。

1.2 两步量子行走的隐形传态系统

通过两步量子行走，移位算子可以带来位置空间和硬币空间之间的纠缠。因此，我们可以将这种纠缠资源用于粒子的隐形传态。具体的讲，我们选择以两个硬币为基础的量子行走系统，通过选择合适的初始态和匹配的测量基，我们可以在双方间成功地隐形传态任何未知量子比特，这使得粒子的隐形传态不再依赖于制备初始纠缠态粒子。

假设Alice想给Bob隐形传态未知量子态 |φ〉=α|0〉+β|1〉，其中 |α|2+|β|2=1。为了完成隐形传态，Alice需要准备两个粒子，A1和Ap，A1是Alice需要要隐形传态的未知量子比特，它也被记为coin1，Ap的粒子态是位置空间的态。同样，Bob准备粒子B，它也被记为coin2。Ap和B的初始态都为 |0〉。经过两步量子行走，粒子A1能完成与粒子B间的隐形传态。

第一步量子行走W(1)为

W(1)=E(1)·(Ap⊗C1⊗A1)

(3)

其中

E(1)=S⊗|0〉1〈0|⊗B+S†⊗|1〉1〈1|⊗B

(4)

在式(3)和式(4)中，C1表示coin1-A1的操作符，我们的协议选择Pauli操作I作为C1操作符。

第二步量子行走W(2)为

W(2)=E(2)·(Ip1⊗H⊗B)

(5)

其中

E(2)=S⊗|0〉2〈0|+S†⊗|1〉2〈1|

(6)

式中：H表示对coin2-B粒子执行Hadamard操作。如果采用的B粒子的初始态为 |+〉 态，这个操作符应被替换为I操作。

然后，Alice将A1粒子和Ap粒子的测量结果λ1和λ2告知Bob，Bob根据λ1和λ2以及表1对B粒子做出相应的Pauli恢复操作，完成B粒子关于A1粒子的隐形传态。

我们详细的推导下两步量子行走过程W(1)和W(2)

W(1)=E(1)·(Ap⊗C1⊗A1)=
(|1〉p〈0|⊗|0〉1〈0|+|-1〉p〈0|⊗|1〉1〈1|)⊗|0〉2·
(|0〉p⊗(a|0〉+b|1〉)1)=
(a|100〉+b|-110〉)p12

(7)

通过分析计算，可以发现，经过W(1)，Ap粒子和A1粒子间产生了纠缠关系，它们的复合态从 (a|0〉+b|1〉)1⊗|0〉p变为了 (a|10〉+b|-11〉)p1。

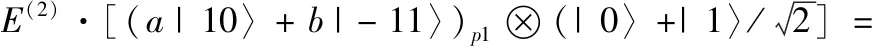
(8)

现在，A1和B也处于纠缠态了，当Alice测量粒子A1时，根据量子力学理论，粒子Ap和B将坍缩到相应的状态

(9)

然后Alice用Q基测量Ap粒子，粒子B也会坍缩到相应的状态

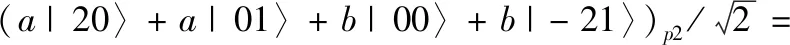
(10)

(11)

最后，Alice将测量结果告知Bob。根据这些测量结果，Bob在粒子B上执行相应的Pauli操作以恢复未知的量子态。测量结果与Pauli操作之间的关系见表1。

表1 测量结果与Pauli操作间的关系

其中，4种Pauli操作表示为

σI=|0〉〈0|+|1〉〈1|

(12)

σZ=|0〉〈0|-|1〉〈1|

(13)

σX=|0〉〈1|+|1〉〈0|

(14)

σZX=|0〉〈1|-|1〉〈0|

(15)

以上表明，量子行走可以用于粒子的隐形传态而不依赖于初始阶段制备纠缠粒子，且硬币状态具有的不可预测的混沌非线性动态行为使得量子行走在理论上具有产生随机空间以抵抗暴力攻击的能力，进而可以研究基于两步量子行走的隐形传态系统在量子秘密共享中的应用。因此，我们提出了一种基于量子行走的量子秘密共享方案。

2 基于量子行走的量子秘密共享方案

协议包括秘密分发者Alice，参与者Bob，Charlie。协议分为粒子准备阶段，秘密信息编码阶段，秘密信息分发阶段，以及秘密信息恢复阶段。Alcie根据规则将需要分享的秘密信息编码为量子态，并将编码粒子拆分为两部分，然后通过量子行走系统将两条加密信息分别隐形传态给Bob，Charlie。在进行窃听检测后，Bob和Charlie根据 Alice 公布的结果测量手中的粒子串，完成隐形传态。此后，Bob和Charlie能够通过合作解密Alice的秘密信息。详细方案如下。

2.1 粒子准备阶段

在粒子准备阶段，Alice，Bob，Charlie准备一些粒子用于量子行走系统的隐形传态。Alice准备粒子串Ap用于量子行走系统的隐形传态，其中Ap=|010203…0n〉。Bob准备初始态为 |0〉 粒子串Bp用于完成与Alice的子秘密信息的隐形传态，其中Bp=|010203…0n〉。Charlie和Bob一样，他准备初始态为 |0〉 粒子串Cp用于完成与Alice的子秘密信息的隐形传态，其中Cp=|010203…0n〉。

2.2 秘密信息编码阶段

在秘密信息编码阶段，Alice生成一串n比特的二进制随机序列L，然后她根据L将n比特的原始信息M编码为两粒子比特串 {|b1c1〉,|b2c2〉,|b3c3〉…|bncn〉}，编码规则见表2。

表2 字符串L,M以及 |bc〉 的相应位值

表2的含义是两粒子比特串 |bc〉 的测量基由L确定，而它们的特征向量由M确定。这意味着当L为0时，|bici〉 的测量基为Z基；当L为1时，|bici〉 的测量基为X基；|bi〉XOR|ci〉 的结果等于Mi。这里 |+〉=1/2(|0〉+|1〉)，|-〉=1/2(|0〉-|1〉)。

然后，Alice按序抽取 |b〉 粒子生成B=|b1b2b3…bn〉，按序抽取 |c〉 粒子生成C=|c1c2c3…cn〉。例如，如果L是0110，M是1011，两粒子比特串 |bc〉 可以生成为 {|01〉,|- -〉,|+ -〉,|10〉}，进而B=|0- +1〉，C=|1- -0〉。只有制备者Alice确切地知道她制备的两粒子比特 |bici〉，B串或C串不能独自地推断出M的信息。此时，秘密信息的编码完成。

2.3 秘密信息分发阶段

在秘密信息分发阶段，Alice通过量子行走系统，将M的子秘密信息B隐形传态给Bob，子秘密信息C隐形传态给Charlie。

(1)Alice随机的在B中插入k比特的诱骗粒子用于窃听检测。通过量子行走系统，Alice将插入诱骗粒子的信息BK隐形传态给Bob，其中BK={b1,b2,b3…bn+k}。我们以bi粒子的隐形传态为例。此前，Alice已经准备了初始态为 |0〉 的粒子Api用于量子行走系统的隐形传态，Alice将bi作为量子行走系统中需要被隐形传态的粒子，其中bi=α|0〉+β|1〉，|α|2+|β|2=1。Bob已在粒子准备阶段准备了量子比特串Bp，他将粒子Bpi作为量子行走系统中的接收粒子，Bpi处于 |0〉 态。现在，整个量子行走系统的初始状态可以写为

|Φ〉=Api⊗bi⊗Bpi=
|0〉p⊗(α|0〉+β|1〉)1⊗|0〉2

(16)

经过第一步量子行走W(1)之后，整个系统态变为

|Φ〉(1)=(α|100〉+β|-110〉)p12

(17)

经过第二步量子行走W(2)之后，整个系统态变为

|Φ〉(2)=(α|200〉+α|001〉+β|010〉+β|-211〉)p12

(18)

(3)Alice将λ1序列和λ2序列公布给Bob，Bob结合表1 对粒子Bp做Pauli恢复操作来获得目标态。此后，Bob完成了来自于Alice的未知粒子的隐形传态，Bpi粒子的态转化为了BKi粒子的态。

(4)在Bob声称收到所有粒子后，Alice开始进行窃听检测。Alice宣布诱饵粒子的位置和测量基，Bob选择合适的测量基来测量每个诱饵粒子，Alice根据Bob的测量结果，她可以评估粒子传输过程中的错误率。如果错误率超过指定的阈值ε，则他们终止该通信，然后从头开始重复该方案，直到错误率可接受为止。否则，Alice继续进行秘密信息分发。

(5)Bob丢弃粒子串Bp中的k比特诱骗粒子获得n比特量子秘密信息Mb。

(6)Alice同样使用量子行走系统将加入k比特诱骗粒子的子秘密信息CK隐形传态给Charlie，本次，Alice分别用γ1和γ2表示测量基X和Q的测量结果序列。

(7)Alice将γ1序列和γ2序列公布给Charlie，Charlie结合表1对粒子Cp做Pauli恢复操作来获得目标态。此后，Charlie完成了来自于Alice的未知粒子的隐形传态，Cpi粒子的态转化为了CKi粒子的态。

(8)在Charlie声称收到所有粒子后，Alice开始进行窃听检测。Alice宣布诱饵粒子的位置和测量基，Charlie选择合适的测量基来测量每个诱饵粒子，Alice根据Charlie的测量结果，她可以评估粒子传输过程中的错误率。如果错误率超过指定的阈值ε，则他们终止该通信，Alice从头开始重复该方案。

(9)Charlie丢弃粒子串Cp中的k比特诱骗粒子获得n比特量子秘密信息Mc。此时，Alice通过量子行走系统完成她与Bob、Charlie的子秘密信息的隐形传态。

2.4 秘密信息恢复阶段

(1)通过量子行走系统，Bob手中持有长度为n比特的量子秘密信息Mb，Charlie手中持有长度为n比特的量子秘密信息Mc。Alice向Bob和Charlie公布决定两个粒子串测量基的字符串L。

(2)Bob和Charlie根据Alice公布的字符串L选择测量基Z或X测量手中的量子秘密信息Mb和Mc，即，在L的位值为0的情况下采用Z基测量，在L的位值是1情况下采用X基测量。Mb和Mc的测量结果分别记为Rb和Rc。

(3)Bob和Charlie可以通过合作，根据MbXORMc恢复出Alice的原始秘密信息M。

3 安全性分析

本方案可以有效抵御内部参与者攻击和外部攻击，保证秘密共享过程的安全性。

(1)内部攻击

Bob无法通过猜测Charlie手中粒子串Mc的测量结果推断Alice的原始信息M，因为只有Alice确切知道她准备的那对粒子 |bici〉。我们假设Bob有50%的概率猜对另一个粒子ci，可以根据统计数据定量评估Bob成功推断整个消息M的概率Pi

(19)

其中，k表示被正确猜测的粒子总数，N表示整个信息M的长度。概率Pi符合二项分布和二项式系数

(20)

通过计算N=100，N=500，N=1000时正确猜测的粒子数k下成功推断整个消息的概率Pi，可知对于不同的N，Pi在区间(0,k)上存在它的最大值 (Pmax(N=100)≈0.0918，Pmax(N=500)≈0.0412，Pmax(N=1000)≈0.0291)，并且随着N的增大而减小。因此，可以得出结论，编码方案可以有效地完成秘密信息编码，Bob无法通过猜测成功推断出原始信息M。

(2)外部攻击

第一种：截获/重发攻击。外部攻击者Eve或者任何参与者无法通过截获/重发攻击有效窃取秘密信息，因为我们在粒子的量子行走过程中添加了诱骗粒子用于避免此类攻击。假设Eve截获量子行走系统中Bob的接收粒子串Bp，然后将另一串粒子序列重新发送给接收方。由于Eve对诱骗粒子的位置和测量基一无所知，接收方会获得不相关的测量结果，这使得粒子传输过程中的错误率增加，导致该对话终止。因此，Eve的截获/重发攻击对该方案无效。

第二种：纠缠攻击。外部攻击者Eve或者任何参与者也无法通过纠缠攻击来获取信息，因为信息在量子信道中传输时，信息被编码为粒子序列并用离散时间量子行走系统加密。假设Eve为获取隐形传态中接收粒子的信息，截获量子行走系统中Charlie的接收粒子串Cp，并用新的粒子e与Cpi缠绕在一起形成一个更大的希尔伯特空间，其中Cpi={|0〉、|1〉、|+〉、|-〉}

E⊗|0e〉=a|0e00〉+b|1e01〉

(21)

E⊗|1e〉=b′|0e10〉+a′|1e11〉

(22)

(23)

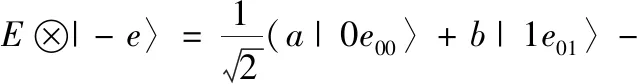
(24)

其中，E是Eve的单一操作矩阵，表示为

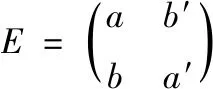
(25)

由E运算符决定的4个 {e00,e01,e10,e11} 纯状态满足归一化条件

(26)

因为EE*=1，a，b，a′，b′满足以下关系

|a|2+|b|2=1,|a′|2+|b′|2=1,ab*=(a′)*b′

(27)

我们可以获得结果

|a|2=|a′|2,|b|2=|b′|2

(28)

如果Eve的攻击粒子处于纠缠态，这种窃听者的干扰将不可避免地引入错误，我们可以以PE的概率检测到窃听者的存在

PE=|b|2=1-|a|2=|b′|2=1-|a′|2

(29)

如果Eve不想引入误差，则总粒子必须与Eve的辅助粒子以直积态相关。然而，在直积态下，辅助粒子e与Cpi粒子之间没有任何相关性，因此Eve没有得到任何有用信息，这说明了纠缠攻击是徒劳的。

4 结束语

在本文中，我们分析了之前主要的基于纠缠态的量子秘密共享方案，以及无纠缠的量子秘密共享方案，并提出了一种基于量子行走的量子秘密共享方案，该方案在初始粒子准备阶段仅采用单粒子并通过量子行走系统完成粒子态的隐形传态。

与以前的量子秘密共享方案不同，我们的方案的优点归纳如下。第一，我们的方案在初始粒子的制备中不需要制备纠缠态粒子，而是采用单粒子，纠缠态粒子制备的困难性可以表明基于纠缠态的量子秘密共享方案在某些情况下是不值得的，毕竟实用性是量子信息论的重要追求。第二，秘密分发者的原始信息被巧妙拆分为子秘密信息并编码为量子态，没有人可以从子集中推断出原始信息。第三，方案的量子通信过程是通过量子行走完成，单粒子在两步量子行走过程中自发地产生纠缠，从而实现了单粒子态的隐形传态，无论是在量子计算还是量子模拟，现已有很多量子行走实验被成功实现，量子行走是量子通信中所需要的。此外，最后的安全性分析表明，基于量子行走的加密量子隐形传态系统，根据其固有的不可预测的混沌非线性动态行为，使得我们的方案能够抵御内部攻击和外部纠缠攻击，在当前技术下是安全可行的。