基于差分和变换的电力电缆故障行波定位方法

田二伟, 刘持涛, 林顺富

(1.国网浙江省诸暨市供电有限公司,浙江 诸暨 311800; 2.上海电力大学, 上海 200090)

电力电缆因其安全、可靠、维护工作量小、通信容量大、使用寿命长、敷设方式美观等优点[1-3],逐步在电力系统中得到了广泛应用,特别在用电需求量大、供电质量要求高、交通拥堵的城市电网中,电缆化程度得到不断提高[4]。虽然电力电缆较架空线故障几率低,但因其一般埋于地下,故障后位于盲区,因此如何快速、准确、经济地定位电缆故障,对电缆线路运行维护、故障解除、保证电网持续可靠供电具有重要意义[2]。

现有电缆在线故障定位方法按原理可分为行波法[5]和阻抗法[6]。行波法因其不受故障类型、线路长度和过渡电阻等因素影响,在电缆故障定位中得到了广泛应用[2]。行波法定位的关键是精确检测出行波的奇异点。目前常用的奇异点检测法有小波变换(Wavelet Transform,WT)、希尔伯特黄变换(Hibert-Huang Transform,HHT)和变分模态分解(Variational Mode Decomposition,VMD)等方法。WT的困难在于小波基函数选择且其会影响Lipschitz指数相同信号的奇异点检测效果,从而影响定位精度[7]。HHT通过经验模态分解(Empirical Model Decomposition,EMD)将信号分为固有模态函数,但EMD易造成模态混叠现象,导致奇异点检测失败[8]。VMD虽克服了模态混叠,但检测的奇异点位置在不同的分解层下会发生偏移[9]。此外,电力电缆运行情况复杂,且考虑到采集装置存在固有缺陷、传输通道易受外界环境干扰等因素,因此实际采集的行波信号会不可避免地引入噪声,会严重影响奇异点的检测。

基于上述背景,本文提出了一种基于差分和变换(Difference Summation Transformation,DST)的电缆故障行波定位方法。首先,分析了基于DST进行行波奇异点检测的基本原理;然后,介绍了利用奇异值分解(Singular Value Decomposition,SVD)降噪和阈值处理的奇异点检测过程;最后,通过仿真模型验证了所提方法的有效性和优越性。

1 差分和变换行波检测法

1.1 DST基本原理

考虑到电缆故障时三相暂态参数存在耦合,采用Karenbauer变换对其进行解耦运算,得到线模和地模的分量信号。本文采用衰减系数小、波速近似恒定的线模信号进行奇异点检测。故障定位的关键步骤是精确检测出线模行波信号(下文统称行波信号)L的奇异点,利用DST可以精确定位L的奇异点时刻。

差分的实质是对离散信号进行微分运算,分为前向差分Δf(i)=L(i+1)-L(i)和后向差分Δf(i)=L(i)-L(i-1)。采用一阶差分,差分和定义为

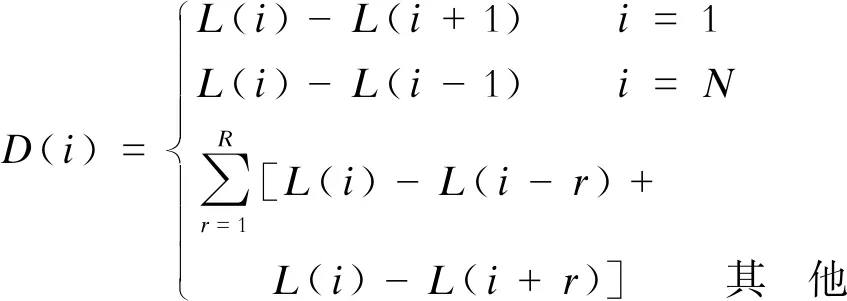
(1)

当2≤i≤N-1时,R满足

(2)

式中:L(i)——故障行波信号采样数据,i=1,2,3,…,N,N为采样点数;

R——以某一时刻为中心的最大差分半径;

h——局部分析窗的宽度。

在某一局部分析窗h内非故障信号是连续且存在一阶导数的,由式(1)可知其差分和为零;而对于故障信号L,其差分和不为零,且奇异点差分和值随h的增大而增大。由此,可以定位出奇异点的位置。

图1为一不含噪故障行波信号及其对应的差分和信号,故障时间为50 018 μs。由图1(b)可知,故障行波信号基于DST后首波奇异点位置检测准确且奇异点数目也正确。

图1 不含噪行波信号及其差分和信号

1.2 SVD降噪

故障行波信号L经DST后,虽然可从差分和信号D中定位奇异点,但受外界环境干扰,实际采集的信号L将不可避免地引入噪声,故D中的背景噪声会影响检测器的精度。为进一步突出D中奇异点的特征峰,采用SVD对其进行降噪处理,基本步骤如下。

步骤1 对一维时间序列差分和信号D进行3行Hankel矩阵变换,得到矩阵D′。

步骤2 对D′做奇异值分解。

D′=USVT

(3)

式中:U——左正交矩阵,U=(u1,u2,u3);

V——右正交矩阵,V=(v1,v2,…,vN-2);

S=(diag(λ1,λ2,λ3),O),且λ1≥λ2≥λ3≥0,均为特征值,O为零矩阵。

由SVD分解性质可得

D′=D′1+D′2+D′3

(4)

步骤4 对D′1做反Hankel变换,以获取降噪后的差分和信号D。

为验证基于SVD降噪的有效性,对图1所示的不含噪故障行波信号添加一白噪声信号,其信噪比为30 dB,如图2(a)所示。对其进行差分和变换后,得到的差分和信号如图2(b)所示,可见虽然差分和信号中的信噪比低于30 dB,但却依然出现了奇异点的特征峰值。经过SVD降噪后的差分和信号如图2(c)所示,可见其背景噪声大大减小,奇异点特征峰值更加明显,验证了SVD降噪的有效性。

图2 含噪故障行波信号的奇异点检测过程

1.3 模极大值提取

采用通用阈值法对差分和信号D进行阈值量化处理,即

(5)

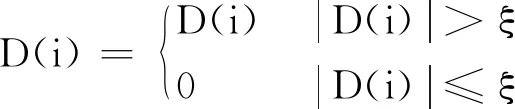
(6)

式中:ξ——选取的阈值;

median(·)——计算中值。

量化后差分和信号D中第一个模极大值点就是首波的奇异值点位置,如图3所示。由图3可见,经过阈值量化后的差分和信号首波奇异点的位置清晰可见。

图3 阈值量化处理后的差分和信号

2 双端行波定位

本文采用双端行波定位[10],测距示意图如图4所示。

图4 双端测距示意

时间监测点分别位于电缆M和N两端,采用GPS时间同步装置,由图4可得测距公式为

(7)

式中:LMF,LNF——故障点F距离M端和N端的长度;

v——行波波速;

tM,tN——故障初始行波到达M端和N端所用的时间;

LT——线缆的总长度,即M和N两点间的距离。

综上所述,基于差分和变换的电缆故障行波定位方法基本流程如图5所示。

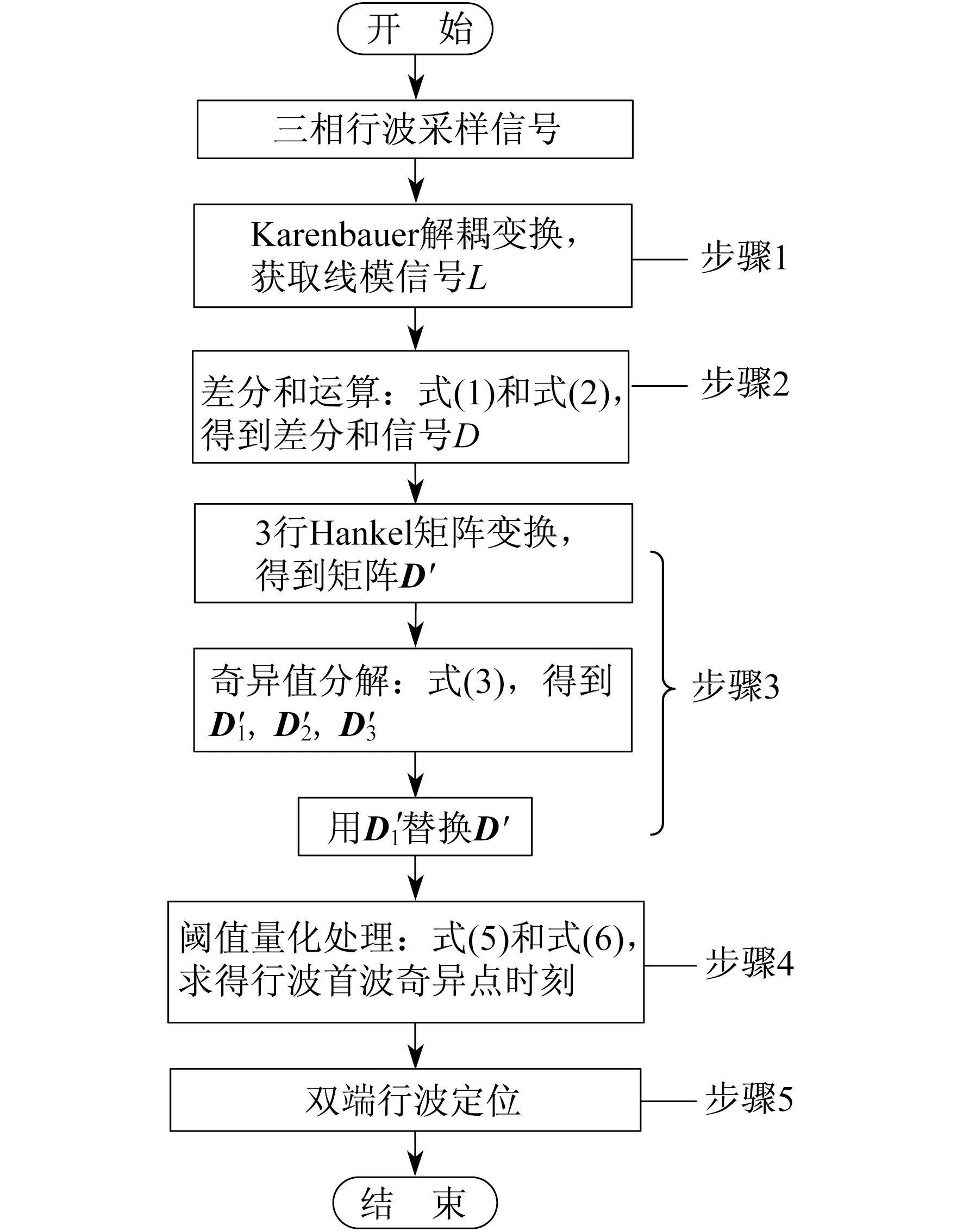
图5 基于DST的故障行波定位流程

3 仿真案例分析

3.1 仿真模型

基于PSCAD/EMTDC搭建的电缆故障仿真模型如图6所示。电缆全长10 km,其参数详见文献[11],故障点绝缘电阻为10 Ω,采样频率为4 MHz。

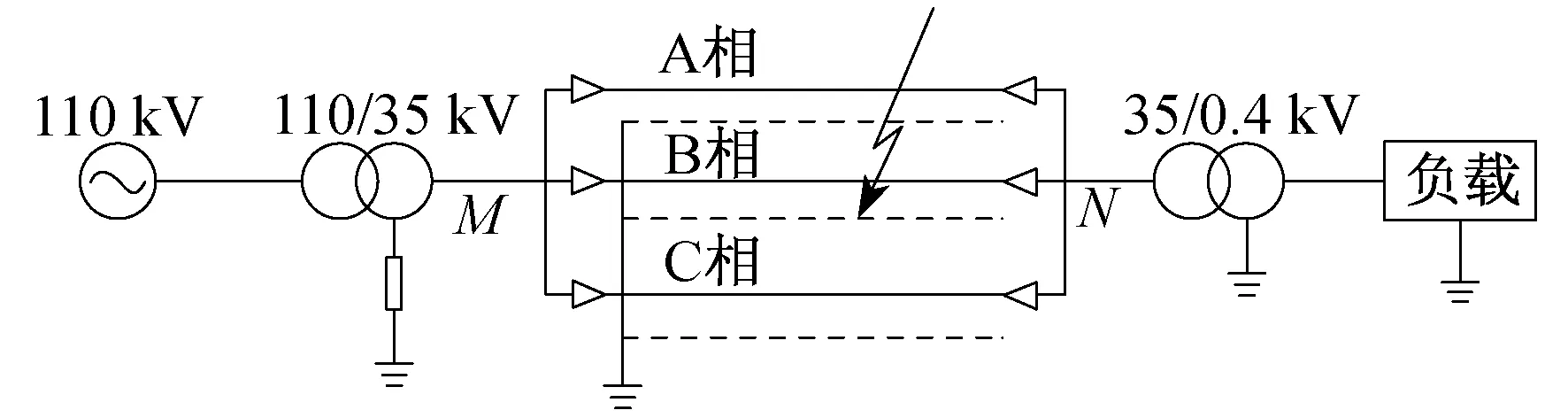
图6 电缆故障仿真模型

3.2 故障行波检测

为验证所提DST方法相比WT和VMD的优越性,对图1所示的故障行波信号,即为图5距离M端2 km处发生A相单相接地故障时M点检测器采集的信号,添加信噪比为30 dB的白噪声。WT和VMD需要对含噪故障行波信号进行前置滤噪,本文采用小波阈值法[12]。3种方法对该行波信号的奇异点检测结果如图7所示。

图7 3种方法的奇异点检测结果

故障点理想时刻为50 018 μs。由图7可知,DST,WT,VMD检测出的奇异点首波时刻分别为50 018.5 μs,50 020.3 μs,50 019.3 μs,误差值分别为0.5 μs,2.3 μs,1.3 μs。可见本文所提方法较WT和VMD具有较强的抗噪能力,且精度较高。

3.3 仿真结果

上述已经得到在距离M端2 km处发生A相单相接地故障时M点检测器采集信号的首波奇异点时刻,为实现故障定位,对N点检测器采集的信号也添加信噪比为30 dB的白噪声。3种方法对该行波信号的奇异点检测结果如图8所示。

由图8可知,DST,WT,VMD检测出的奇异点首波时刻为50 053.3 μs,50 055.7 μs,50 054.1 μs,结合上述M点检测出的奇异点首波时刻,代入式(7),计算得故障定位结果和误差如表1所示。

表1 单相接地故障时3种方法的故障定位结果

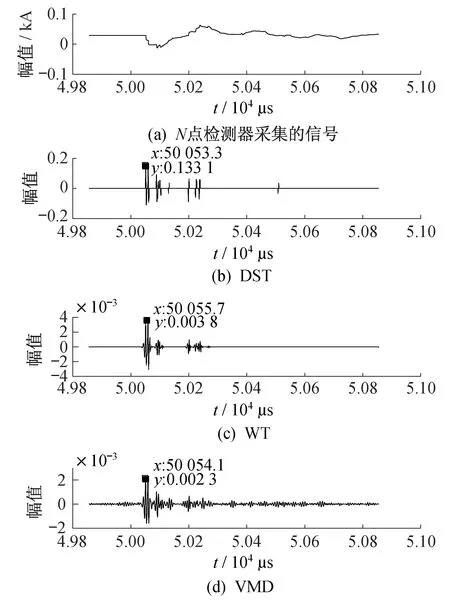
图8 N点检测器采集的信号及3种方法的奇异点检测结果

为进一步验证本文所提方法的有效性和优越性,分别在图6距离M点2 km,5 km,7 km处设置不同的故障类型,且同样在采集的故障行波信号中添加信噪比为30 dB的白噪声,采用两端测距法,3种方法的定位结果和相对误差如表2所示。表2中,AG,AB,ABC分别表示单相接地、两相短路和三相短路故障。

由表2可知,采取本文方法仅在距离M端2 km处发生两相短路时相对误差较WT和VMD大,其余情况下均较其他两种方法小。由此可见,与WT和VMD相比,本文所提方法精度高且定位误差满足实际工程需求。

表2 3种方法故障定位结果

4 结 语

本文提出了一种基于差分和变换的故障行波定位方法,可以准确检测首波的奇异点时刻,通过奇异值分解和阈值量化处理,可使奇异点特征峰值更加明显。仿真结果表明,相比于小波变换和变分模态分解,本文提出的方法具有较强的抗噪能力且定位精度较高,可以满足实际工程需要。