利用微动方法研究吉林市浅层二维剪切波速度结构

李洪丽

(吉林大学 地球探测科学与技术学院，长春 130026)

0 引言

微动方法没有固定的震源，它是利用地球本身存在的由于人类活动和自然现象等带来的微动信号来研究地壳浅层信息。该方法以其操作简单、施工方便、探测成本低、对周围环境无破坏、适用范围广等优势，被越来越多的国内、外研究者采用。通过微动的频谱特性来研究微动在时间和空间上的变化,进而获得探测区域地壳浅层速度结构。地壳浅层速度结构能为活动断裂、强地面运动模拟、地热资源勘查以及地震工程场地评估等地质问题提供帮助[1]。高分辨S波速度结构反演还能很好地反映地下介质低速层的空间变化，为地球浅部圈层耦合性关系、强震孕震环境及区域动力学机制等研究提供重要参考[2]。随着国内、外关于地震学理论和方法研究的不断发展，基于地震背景噪声数据的微动方法在研究地壳浅层速度结构成像、地球内部波速结构随时间变化关系,以及测定地震水平位置等方面获得了众多有意义的研究成果。在地壳浅部数十米至数百米深度的波速结构探测中，微动探测方法已经在地质调查、土木工程等实际应用领域得到了大力推广，并且取得了良好的应用效果。

从微动信号中提取面波频散曲线的方法主要有，空间自相关法(SPAC 法)、频率-波数法(F-K 法)、H/V谱比法等，其中空间自相关法最为常用[3-4]。Aki[5]提出了空间自相关法的概念，研究了在平稳随机波动理论假设下一维和二维的空间自相关理论及应用实例;何正勤等[6]采用空间自相关法，研究了地壳浅层1 km～2 km深度的横波速度结构，通过与钻井结果比对，验证了该方法对于确定物性差异性大的地层界面是可靠的；徐佩芬等[7]基于自相关法提取地震台站微震信号相速度频散曲线，并反演得到地壳浅层S波速度结构，结果与人工地震探测结果较为吻合，验证了SPAC法估算地壳S波速度结构的可行性;李细兵等[8]利用空间自相关法获得一个凹陷盆地基本速度结构和各层深度分布范围，结果显示该区域的土层结构接近人工地震勘探解释结果；张宝龙等[1]利用密集台阵接收的数据，基于微动和面波层析成像方法,获得了在五大连池火山区尾山火山锥地区地表至700 m深度的地壳浅层三维S波速度结构；谢朋等[9]利用微动探测方法获取潜江市浩口中学地下介质结构分层，并与钻孔结果对比，表明微动探测方法能较好地分辨地层结构；盛勇等[10]通过提取频散曲线和视S波速度分层，描述了地层的速度结构及地热异常特征，表明微动勘探能有效地在地热资源勘查中应用。上述研究成果表明，微动法近年来在地质调查实际中应用已经十分普遍，并且该方法也是行之有效的研究方法之一。

1 野外数据采集与研究方法

采用微动方法(空间自相关)，对吉林市某地区地热勘探区域地壳浅层S波速度结构进行研究，研究过程包括野外采集数据，对采集到的原始地震数据进行瑞雷波相速度频散曲线提取，再对提取得到的频散曲线进行拟合反演，进而获得研究区域地下1 000 m 深度的地壳浅层二维S波速度结构剖面。野外观测仪器为短周期地震仪(图1)10台，为了减小由于噪声源方位分布不均匀而带来的对面波频散曲线可靠性的影响，野外观测所用10台短周期地震仪布置位置采用多重圆观测系统(图2)。每组如图2所示布设10台短周期地震仪，其中中心点为观测目标点，放一台短周期地震仪，外围距中心点的距离分别为50 m、100 m、200 m，共计观测5个目标点，形成一条观测剖面，每个目标点观测时间不少于15 h，研究深度为地表以下1 000 m以内地层。五个观测目标点，分别记作S4-1、S4-2、S4-3、S4-4、S1-8。

图1 短周期地震仪

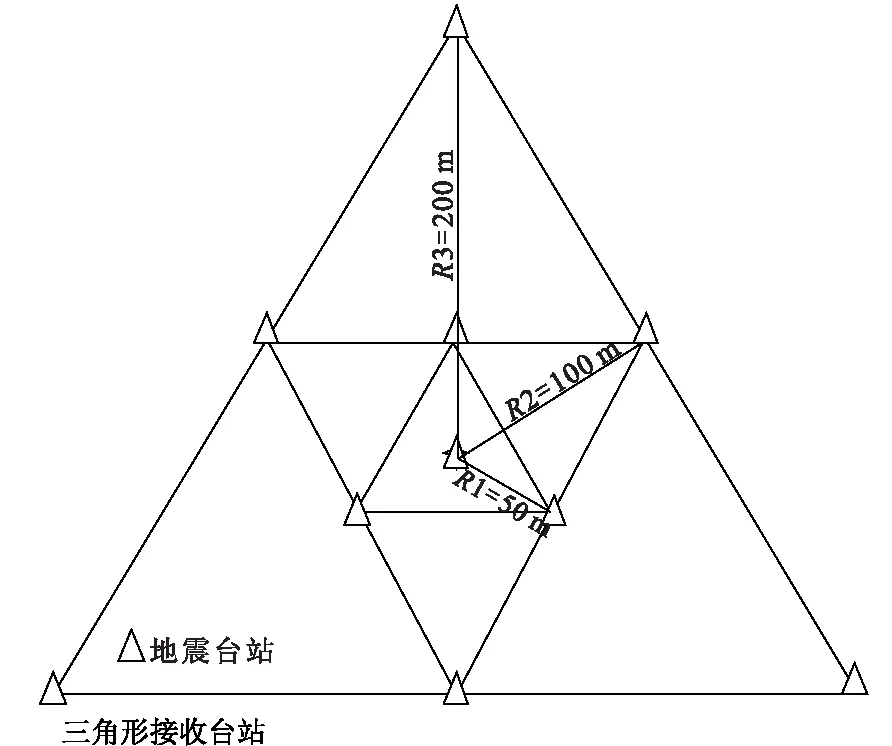
图2 微动单点观测系统(三重圆形台阵)示意图

微动方法主要目的是，从观测的噪声信号中提取瑞雷波相速度频散曲线，并用瑞雷波相速度频散反演地下S波速度结构，所以提取准确的频散曲线至关重要。本研究采用空间自相关(SPAC)方法，该方法是基于微动信号在时间和空间上平稳随机分布这一假设。在该假设条件下，对相距为r的两个点的微动记录作空间相关运算。Aki给出了方位平均后的空间自相关函，数可以用零阶贝塞尔函数来表示：

ρ(r,f)=J0(2πfr/c(f))

(1)

式中:r为两台站间的距离;f为频率;c(f)为瑞雷波相速度;ρ(r,f)为方位平均后的自相关系数;J0为第一类零阶贝塞尔函数[5]。式(1)适用于基阶面波能量为主，利用垂向记录分量进行空间自相关提取瑞雷面波频散的情形。

空间自相关系数的计算大致分为时域(窄带滤波法)和频域两大类。时域空间自相关系数求取的步骤为：①获取记录良好的原始记录，对每段选取的记录平均分成若干段，分段时要保证可以覆盖足够多的频率信息；②对数据进行不同中心频率的窄带滤波处理，得到以滤波器中心频率为自变量的近似单色波记录；③将单频记录的距离为r的台站对按式(2)计算空间自相关系数，并将相同台站对的结果进行平均；④循环步骤②和步骤③，计算出一系列频率值所对应台站对的空间自相关系数，对所得的空间自相关系数按式(3)两两取方位平均，得到用于计算频散的平均自相关系数。

(2)

(3)

空间自相关系数的频率域计算公式为式(4)。

(4)

平面上圆形排列台阵中各台站的位置一般用极坐标形式表示。以参考点为圆心，θ为台站方位角，S(r,θ,f)为参考点记录与其他记录点的互功率谱，S(0,f)和S(r,f)分别为参考点和与其距离r的另一点记录的自功率谱；Re为取实部，确保空间自相关系数为实数。

频域计算相对于时域计算的优势是去掉了多次窄带滤波过程，只利用一次傅里叶变换后完全在频率域内进行计算，因此大大加快了运算速度,所以本研究是在频率域进行计算的。

频域空间自相关系数求取的步骤：①选取良好的记录数据，将数据分段；②将分段后的数据进行傅里叶变换得到频率域数据，在频率域内分别计算对应数据段的自功率谱和互功率谱，然后将各段数据结果进行平均；③将平均后的自功率谱和交叉谱结果代入式(4)计算方位平均，便可得到方位平均的空间自相关系数。

2 野外数据处理及结果讨论

野外数据采集过程中尽量避开有大量人为因素干扰的区域，经过5个观测点累计50台短周期地震仪的记录，完成5个观测目标点的微动信息数据采集工作。其中观测目标点S4-1的部分原始采集数据波形如图 3 所示，可以看出各个地震仪记录波形一致性较好，表明采集到的微动信息可靠。

图3 S1点的10台短周期地震仪接收的部分连续地震背景噪声数据

在计算各观测目标点空间自相关系数前，先整理5个观测目标点的各地震仪接收到的原始数据，再分别进行去均值、去倾斜、去尖脉冲等数据预处理工作。将每个短周期地震仪垂直分量噪声数据按照时间进行分段处理，然后对所有分段数据进行傅里叶变换，按照用一台短周期地震仪的傅里叶谱与另一个台的傅里叶谱的共轭计算自相关系数，再对自相关系数波形进行平滑处理，得到各观测目标点对应的自相关系数曲线。数据处理过程中将信噪比较低、未能呈现第一类零阶贝塞尔曲线形态的自相关系数曲线剔除。最后通过分析自相关系数波形的零点和极点，与第一类零阶贝塞尔函数零点和极点进行拟合，得到五个观测目标点的面波相速度频散曲线(图4)。

图4 瑞雷面波相速度频散曲线

采用CPS330软件分别对上述5个观测目标点的面波相速度频散曲线进行线性反演，求取各观测目标点的一维速度模型[11]。再分别对各观测目标点的一维速度模型进行插值处理并合成，最终获得该研究区域地表以下1 000 m以内的浅表地下介质二维S波速度剖面(图5)。

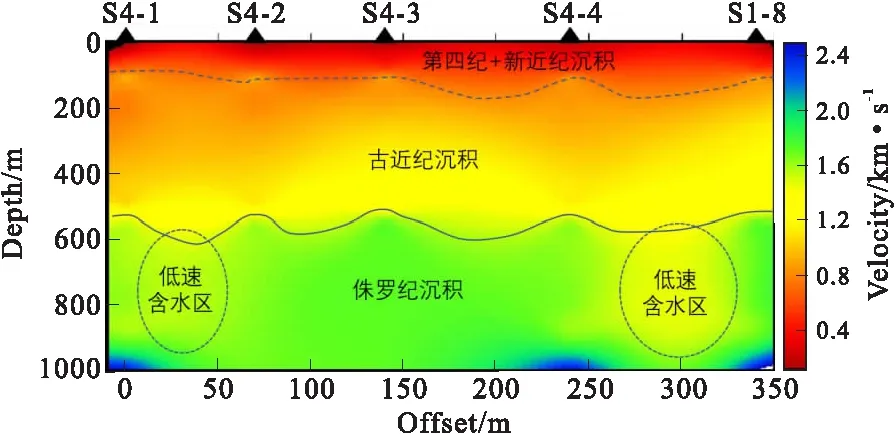
图5 研究区域地壳浅层二维S波速度剖面

S波速度对于地层内的流体、温度变化和介质性质十分敏感。S波速度结构研究有助于分析研究区域地下介质物理状态。地下介质岩性是影响地震波速的决定因素，介质中存在的裂隙和孔隙度是基本影响因素。另外，地下介质孔隙中的不同填充物、介质的风化和破碎带以及埋藏深度都会对地层波速产生影响。结合吉林市周边地区地层划分表，从获得的1 000 m深度的S波速度结构剖面图(图5)中可以分析出：研究区域内S波速度整体由地表至地下随地层的深度增大呈增大趋势，研究区域在深度上可分为三层，第一层速度较低，底界面深度在100 m～150 m左右，为第四纪和晚新生代(新近纪)沉积地层；第二层S波速度在1 000 m/s左右，底界面深度在550 m左右，推测为早新生代(古近纪)沉积地层；第三层地层速度约1 800 m/s，推测为中生代(侏罗纪)沉积地层。由于不同岩性的地层速度不同，再者由于沉积年代以及沉积环境的差别，即使是同一岩性的地层速度也会存在一定的差异，所以依据单一S波速度参数所分层位可能具有一定的误差。

另外，由于地震波速在气体和液体中传播速度低于在固体(岩石骨架)中的传播速度，裂隙的存在会使地震波传播速度减慢。由此可推测出在第三层中显示的两个明显的低速区可能为含水区。

3 结论

利用由10 台短周期地震仪组成的短周期地震仪台阵，在吉林某工区开展了连续地震背景噪声观测，共选取观测目标点5个，组成一个观测剖面。利用微动方法首次获得该区域地表至地下1 000 m深度的浅层S波速度结构剖面。结果表明：地表至地下1 000 m之间S波速度整体随深度具有线性增加的趋势；研究区整体分为三层：由浅至深依次为第四纪和新近纪沉积层，古近纪沉积层和中生代(侏罗纪)沉积层；在第三层中550 m～950 m区域存在两个低速异常区，推测为富含水区域。该微动观测结果将为该区域今后开展地热探测、野外地质调查等研究工作提供重要参考。