重积分中两类面积元素之辨析

张 辉， 王兆强， 王 静

(火箭军工程大学 基础部，陕西 西安 710025)

0 引言

重积分是多元函数积分学的重要内容，如何正确计算二重积分是需要解决的关键问题。 而在二重积分的计算以及应用中，常常需面对一个至关重要的概念：面积元素。 为使学生能够深刻理解面积元素，下面将对二重积分面积元素和曲面的面积元素进行再研究，并给出两类面积元素之间的内在联系，然后得到基于元素法的两类面积元素的表达形式，并辅以典型例题供参考学习，使初学者灵活使用，达到事半功倍、举一反三的效果。

为了确保二重积分的存在性，假设被积函数均是连续或分块连续。

1 二重积分面积元素的再研究

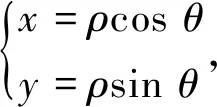
可见，面积元素dσ是与平面坐标系的选取密切相关的。 许多学生对极坐标系中面积元素的表达式ρdρdθ理解较为困难，甚至有些学者[2]认为把ρdρdθ作为极坐标系中的面积元素的说法不太严格，而笔者认为教材中关于面积元素的表述是正确的，本质上就有dσ=dxdy=ρdρdθ。

究竟是什么原因呢？事实上，教材中采用了两种方法介绍直角坐标系和极坐标系中面积元素之间的关系。第一种方法是从二重积分的定义出发，利用直角坐标系和极坐标系之间的内在联系得到二重积分所对应的特定和式的极限在极坐标系中的形式。一般对直角坐标系中面积元素为dxdy较好理解，但对极坐标系中面积元素为ρdρdθ很难理解，不应该是dρdθ吗？

笔者认为产生这样错误想法的主要原因是没有理解直角坐标系和极坐标系的本质联系。对于平面xOy直角坐标系，极坐标系的确定是以O点为极点，Ox轴正向作为极轴OA的。给定平面OA极坐标系，直角坐标系的确定是以O点为原点，OA轴作为横轴Ox的正向，逆时针旋转π/2得到纵轴Oy的正向。同时，积分区域D在直角坐标系和极坐标系中的形状是不发生改变的。

我们再来分析其面积元素的内在联系。从元素法的角度来看，如图1所示，Δσ面积近似等于两边长分别为dρ和ρdθ的矩形的面积ρdρdθ，故将ρdρdθ作为极坐标系中面积元素的表达式。这说明了极坐标中面积元素恰好为ρdρdθ，上述问题得以较好解决。

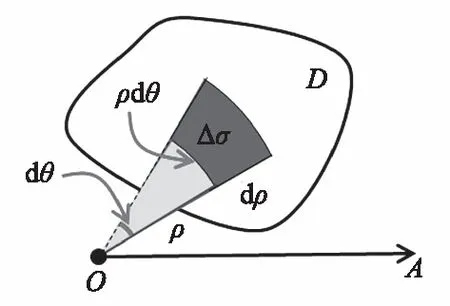
图1 极坐标系中的面积元素Fig.1 Area element in polar coordinate system

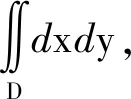
第一种方法是将点(x,y)和点(ρ,θ)看成是同一平面上的同一个点，只是采用不同的坐标而已，而换元法是将直角坐标平面ρOθ上的点(ρ,θ)变为直角坐标平面xOy上的点(x,y)，将直角坐标平面ρOθ上闭区域D′变为直角坐标平面xOy上的闭区域D，如图2所示。

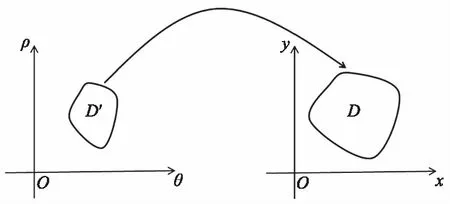
图2 换元法中积分区域的转换Fig.2 Conversion of integral regions in conversion method

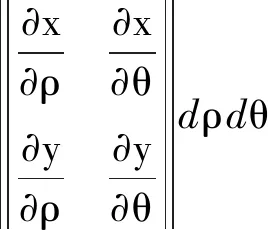
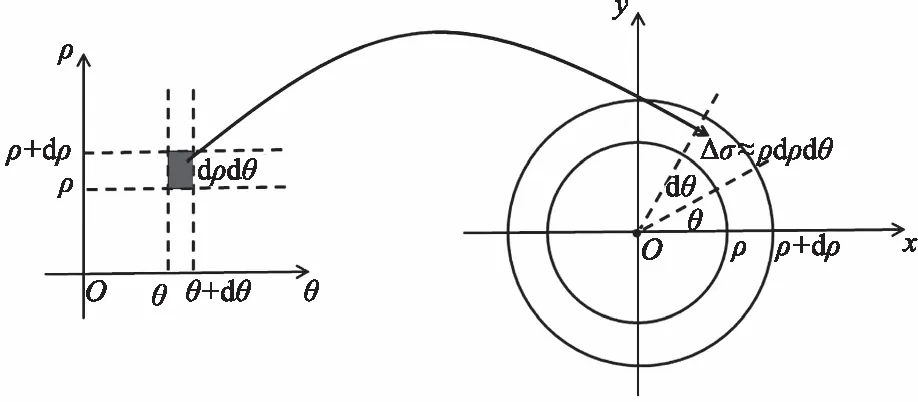
图3 换元法中面积元素的转换Fig.3 Conversion of area elements in conversion method

考察一个具体例子进行说明，对于半径为a(a>0)的平面圆面D={(x,y)|x2+y2≤a2}，在极坐标系中可以表达为D={(ρ,θ)|0≤ρ≤a，0≤θ≤2π}，其本质上仍然刻画的是该圆面，而在换元法中对应平面直角ρOθ坐标系中的区域为矩形域，如图4所示。

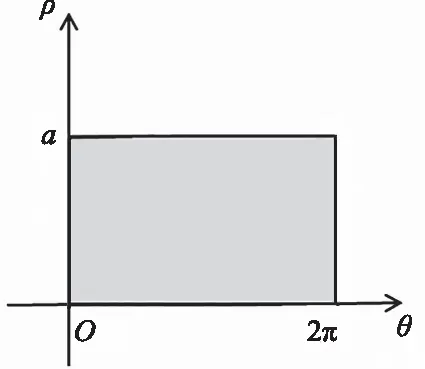
图4 换元法中的矩形域Fig.4 Rectangular domain in exchange method

对于极坐标变换的逆变换

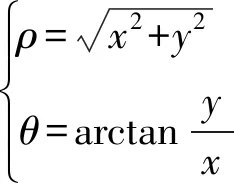
或

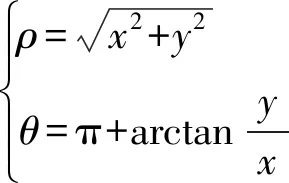
由换元法可得

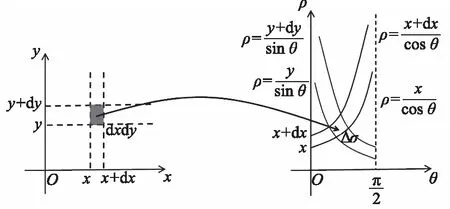
图5 换元法中面积元素的转换Fig.5 Conversion of area elements in conversion method

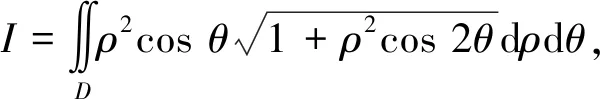
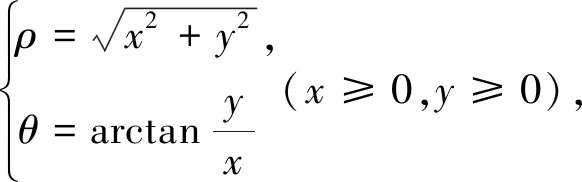
由换元法得，

图6 积分区域的变换Fig.6 Transform of integral region

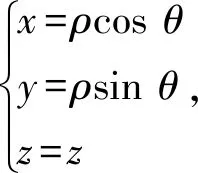
同理，对于球面坐标变换情形也是成立的。

2 曲面面积元素的再研究

在二重积分及其应用中，常常会遇到两类面积元素，一是二重积分的面积元素dσ，二是计算曲面面积时曲面的面积元素dA。笔者在第一部分详细介绍了面积元素dσ不同类型的表达式及其内在联系。而对于曲面的面积元素dA，与曲面S方程的给定形式有关。下面分3种情形讨论。

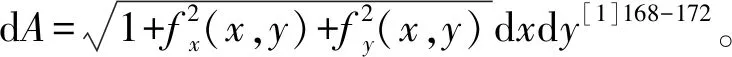
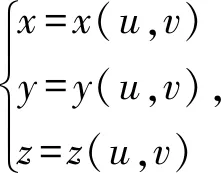
则有

进而

同理

代入可得

由第一部分分析可得，

同理

dydz=|yuzv-yvzu|dudv，dzdx=|zuxv-yvxu|dudv，

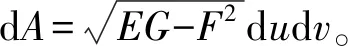
情形3，若曲面S方程由方程F(x,y,z)=0所确定的二元隐函数z=f(x,y)给定，由隐函数存在定理知，

即有

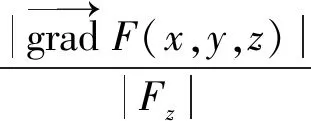
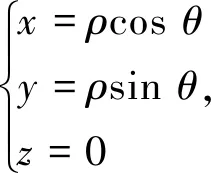
则

3 曲面的面积元素的再研究

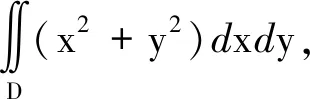
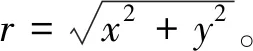
图7 旋转曲面的面积元素Fig.7 Area elements of rotating surfaces

4 结束语

如何把握不同类型面积元素的本质及其内在联系，这是初学者对于重积分首先要面对的问题。要从简单、基础的一元函数积分学过渡到对复杂、抽象的多元函数积分学的学习中确有难度，但是似乎越难的学科就越具有其独特的魅力，使你不断地花心思去学它、理解它、体会它，从而真正感到它的内在美。