高考复习冲刺阶段“能力型”问题的教学策略
2020-11-15湖南杨育球
湖南 杨育球
能力型问题是高考命题创新的亮点题型,其特点是:通过给出新知识、新方法或新情境等信息,要求考生用自己已掌握的知识、技能和方法,借助题干信息解决新问题.它主要用来考查考生临场阅读、提取信息、处理信息所需的各种思维方法(如比较、分类、分析、综合、归纳、演绎、类比等)及分析问题和解决问题的能力.在紧张的高考考前冲刺备考阶段,如何使我们的复习教学取得事半功倍的效果?无疑重视能力型问题是使复习教学的成效更上一层楼的有效途径.
一、通过“新信息”能力型问题的教学,培养学生思维的创新性
所谓“新信息”能力型问题,就是在常规题的基础上,要么给出新的定义,要么将有关信息进行迁移,或者针对某一问题展开研究性学习,进而产生的一些“一反常态”的新型问题.这类问题要求考生能够针对新颖的信息、情境和设问,选择有效的方法和手段收集信息,综合与灵活地应用所学的数学知识、思想和方法,进行独立思考、探索和研究,提出解决问题的思路,创造性地解决问题,从而培养学生思维的创新性.

A.a※b=b※a
B.μ(a※b)=(μa)※b=a※(μb)(μ∈R)
C.(a+b)※c=a※c+b※c
D.若e是单位向量,则|a※e|>|a|
以上结论一定正确的是( )
解析:当a,b共线时,a※b=2|a-b|=2|b-a|=b※a,当a,b不共线时,a※b=a·b=b·a=b※a,故A正确;当μ=0,b≠0,μ(a※b)=0,(μa)※b=2|0-b|≠0,故B错误;当a+b与c共线时,则存在a,b与c都不共线,(a+b)※c=2|a+b-c|,a※c+b※c=a·c+b·c,显然2|a+b-c|≠a·c+b·c,故C错误;当e与a不共线时,|a×e|=|a·e|=|a|·|e|=|a|,故D错误.综上,应选A.
点评:本题是“新定义运算”的信息创新问题.解决这类创新题的关键是“读懂法则,紧扣法则,适当运算,适当用特例或特值处理”. 这类创新题要求考生要善于抓住新信息的主干,灵活运用所给法则解决问题.
【例2】定义函数fn(x)=(1+x)n-1(x>-2,n∈N*且n>1).
(Ⅰ)求证:fn(x)≥nx;
(Ⅱ)是否存在区间[a,b]⊆(-∞,0],使函数h(x)=f3(x)-f2(x) 在区间[a,b]上的值域为[ka,kb]?若存在,求出最小的k值及相应的区间[a,b];若不存在,请说明理由.
解析:(Ⅰ)令g(x)=fn(x)-nx=(1+x)n-1-nx,则g′(x)=n(x+1)n-1-n=n[(x+1)n-1-1],当-2
(Ⅱ)假设存在满足条件的区间[a,b],则h(x)=f3(x)-f2(x)=x(1+x)2,所以h′(x)=(1+x)2+x·2(1+x)=(1+x)(1+3x).

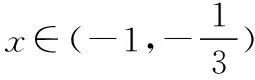
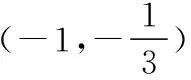
其大致图象如图所示:


方法2.由题易知k>0,b=0.


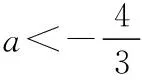

点评:本题涉及函数、导数、函数值域和不等式等知识,是融合“新定义迁移、综合性、开放性和探索性”于一体的函数与导数探索性问题,重在考查导数知识以及数形结合思想的综合运用.存在型探索问题是近年来高考的热点题型,求解这类问题,应做到大胆预测、小心求证、思路清晰、过程规范.求解函数与导数的探索性问题主要有两个途径:一是先假设符合题意的条件存在,然后把结论作为条件,进行分析,探求出条件后,再进行证明;二是先假设符合题意的条件存在,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;反之,肯定结论. 求解条件组合型问题,需通过对条件的反复组合试验,进行逐一尝试探求.
二、通过“新方法”能力型问题的教学,培养学生思维的灵活性
所谓“新方法”能力型问题,就是在问题的题干中给出的信息是一种全新的思维方式或方法型的知识.在解答这类能力型试题时,考生必须把试题所给的新知识纳入到自己已有的知识结构中来,与已有知识整合形成新的知识结构,再运用它来解决问题,从而培养思维的灵活性.
【例3】三位同学合作学习,已知区域Ω={(x,y)|1≤x≤2,2≤y≤3}内的数对(x,y)满足不等式xy≤ax2+2y2,求a的取值范围”提出了各自的解题思路.甲说:“可视x为变量,y为常量来分析”.乙说:“寻找x与y的关系,再作分析”.丙说:“把字母a单独放在一边,再作分析”.参考上述思路,或自己的其他解法,可求出实数a的取值范围是________.
答案:[-1,+∞)
解析:方法1.甲的思路:原不等式可化为f(x)=ax2-yx+2y2≥0,当x∈[1,2]时,恒成立.
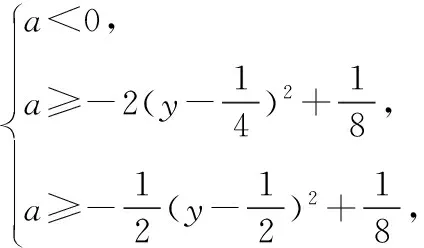
因为y∈[2,3],所以-1≤a<0;
②当a=0时,f(x)=-yx+2y2,因为y∈[2,3],所以f(1)=2y2-y∈[6,15],f(2)=2y2-2y∈[4,12],所以f(x)>0,符合题意;
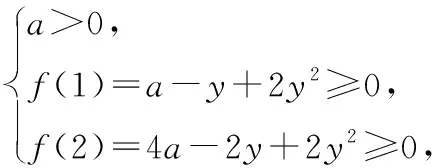
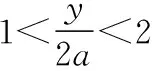
综上所述,a∈[-1,+∞).

当Ω={(x,y)|1≤x≤2,2≤y≤3}时,1≤t≤3.
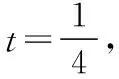


【例4】已知向量a、b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是________,最大值是________.
解析:根据条件建立平面直角坐标系.如图,记∠AOB=α,则0≤α≤π.
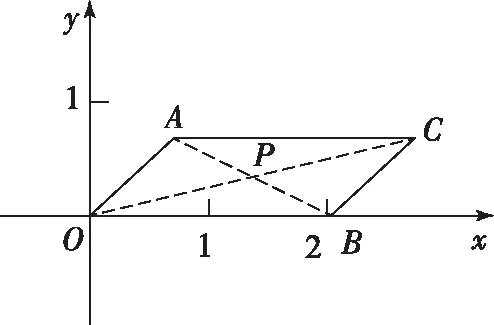
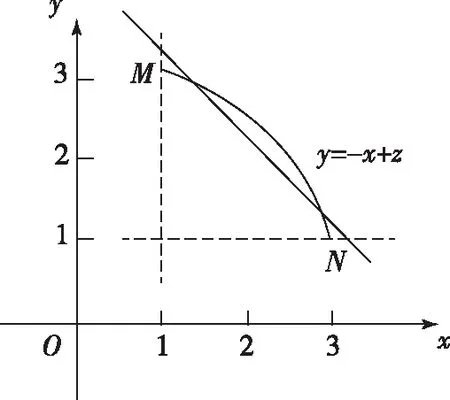
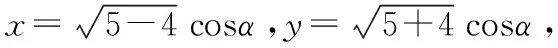
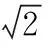

点评:本题充分挖掘向量与解析几何都具有数与形的双重身份这一特点做文章,利用圆的几何性质和向量加法运算的几何意义,转化为两点间的距离进而借助新“圆”模型,数形结合解决问题,很好地考查了考生思维的灵活性.
本题首先依据向量加、减运算的几何意义构造平行四边形,然后利用余弦定理将两向量和与差的模表示为角的三角函数,进而换元来构造“圆(弧)”模型,利用直线与圆的位置关系求解,充分体现“构造思想”在解题中的运用和直观想象素养的渗透.本题的两空属并列关系.
三、通过“新情境”能力型问题的教学,培养学生思维的深刻性
所谓“新情境”能力型问题,就是在问题中设置新的情境、或选择不同条件,给出阅读材料,抑或以数据(表格或图象)的形式给出,要求考生在观察、分析、推理、比较、概括和探索的基础上,找到解决问题的方法和途径,从而培养思维的深刻性.
【例5】在①b1+b3=a2,②a4=b4,③S5=-25这三个条件中任选一个,补充在下面问题中,若问题中的k存在,求k的值;若k不存在,说明理由.
设等差数列{an}的前n项和为Sn,{bn}是等比数列,________,b1=a5,b2=3,b5=-81,是否存在k,使得Sk>Sk+1,且Sk+1 注:如果选择多个条件分别解答,按第一个解答计分. 解析:因为在等比数列{bn}中,b2=3,b5=-81,所以公比q=-3,从而bn=b2(-3)n-2=3×(-3)n-2,所以a5=b1=-1. 若存在k,使得Sk>Sk+1,即Sk>Sk+ak+1,从而ak+1<0; 同理,若使得Sk+1 方法1:若选①,由b1+b3=a2,得a2=-1-9=-10,所以an=3n-16,当k=4时,满足a5<0,且a6>0成立. 若选②,由a4=b4=27,且a5=-1,得数列{an}为递减数列,故不存在ak+1<0,且ak+2>0. 又k∈N*,从而k=4满足题意. 若选②或选③,仿解法1解决. 点评:本题是条件和结论均开放的探索性问题,在不同的条件下进行了结论的探索,考查了等差和等比数列知识的综合运用,以及数学运算、逻辑推理等数学核心素养. 【例6】几何特征与圆柱类似,底面为椭圆面的几何体叫做“椭圆柱”. 图1所示的“椭圆柱”中,A′B′,AB和O′,O分别是上、下底面两椭圆的长轴和中心,F1,F2是下底面椭圆的焦点.图2是图1“椭圆柱” 的三视图及尺寸,其中俯视图是长轴在一条水平线上的椭圆. 图1 图2 (1)若点M,N分别是上、下底面椭圆的短轴端点,且位于平面AA′B′B的两侧. ①求证:OM∥平面A′B′N; ②求平面ABN与平面A′B′N所成锐二面角的余弦值. 解析:(1)①连接O′M,O′N,∵O′O⊥平面A′B′N′,O′M⊂平面A′B′N′,∴O′O⊥O′M. ∵O′M⊥A′B′,O′O⊂平面AA′B′B,A′B′⊂平面AA′B′B,A′B′∩O′O=O′,∴O′M⊥平面AA′B′B. 类似可证得ON⊥平面AA′B′B,∴O′M//ON. 又∵O′M=ON, ∴四边形ONO′M为平行四边形,∴OM∥O′N. 又∵OM⊄平面A′B′N,O′N⊂平面A′B′N, ∴OM∥平面A′B′N. ∵z轴⊥平面ABN,∴可取平面ABN的一个法向量n1=(0,0,1). 设平面ABN与平面A′B′N所成锐二面角为θ, 又∵NF1,NF2⊂平面ABN,∴NN′⊥NF1,NN′⊥NF2. 点评:本题以由平面图形向空间图形进行升维类比得到“椭圆柱”,创设新的问题情境,结合三视图证明线面平行和求解二面角的余弦值;进而直观判断tan(α+β)的取值范围,并进行了证明.多方面的知识、方法融合于一题,可谓是一道研究性学习的经典试题. 在高考复习冲刺阶段时间紧、任务重的情况下,如何通过能力型问题的教学使学生数学思维能力得到进一步提升,是摆在每一位高三老师面前的课题.为数不少的老师往往以没有时间为借口,不愿花费精力指导学生对一些具有数学思维价值的典型问题做深入地探索,而是让学生一味地做题,一题一题的刷,整套整套的做,只是为“解题”而解题,而不去考虑如何“解题”.这样做的结果往往适得其反,表面上看学生每天都沉浸在高压的学习下,但学生复习效率低下,并没有太大的效果,当学生在高考中遇到数学思维性强且需要探究数学本质的能力型问题时,就束手无策了.问题解决是数学高考的“主旋律”,即使是高考前的复习冲刺,教师也要转变教学理念和教学方式,对一些能力型试题,多研究、多探索和多归纳,唯有如此,才能达到提高复习效率的目的.