THE PERTURBATION PROBLEM OF AN ELLIPTIC SYSTEM WITH SOBOLEV CRITICAL GROWTH∗
2020-11-14QiLI李奇
Qi LI (李奇)
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China
E-mail : qili@mails.ccnu.edu.cn
1 Introduction
In this paper, we consider the following coupled elliptic system:
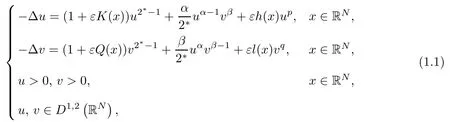
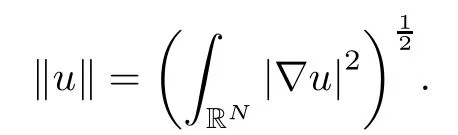
Systems like (1.1) are general versions of nonlinear elliptic systems, such as the Bose-Einstein condensate, that arise in mathematical physics. We refer to [1–9, 21, 22]and references therein for more on systems (equations) with both critical and subcritical exponent. In particular, the case in which the coupling is nonlinear and critical has received a great deal of attention recently, and significant progress has been made in the last thirty years since the celebrated work of Brezis and Nirenberg [10].
Denote HRN= D1,2(RN)× D1,2(RN) with the normWe call a solution (u,v) positive if both u and v are positive, (u,v) nontrivial ifand (u,v) semi-trivial if (u,v) is of the form (u,0) or (0,v). It is well known that solutions of problem (1.1) can be attained by finding nontrivial critical points of the functional
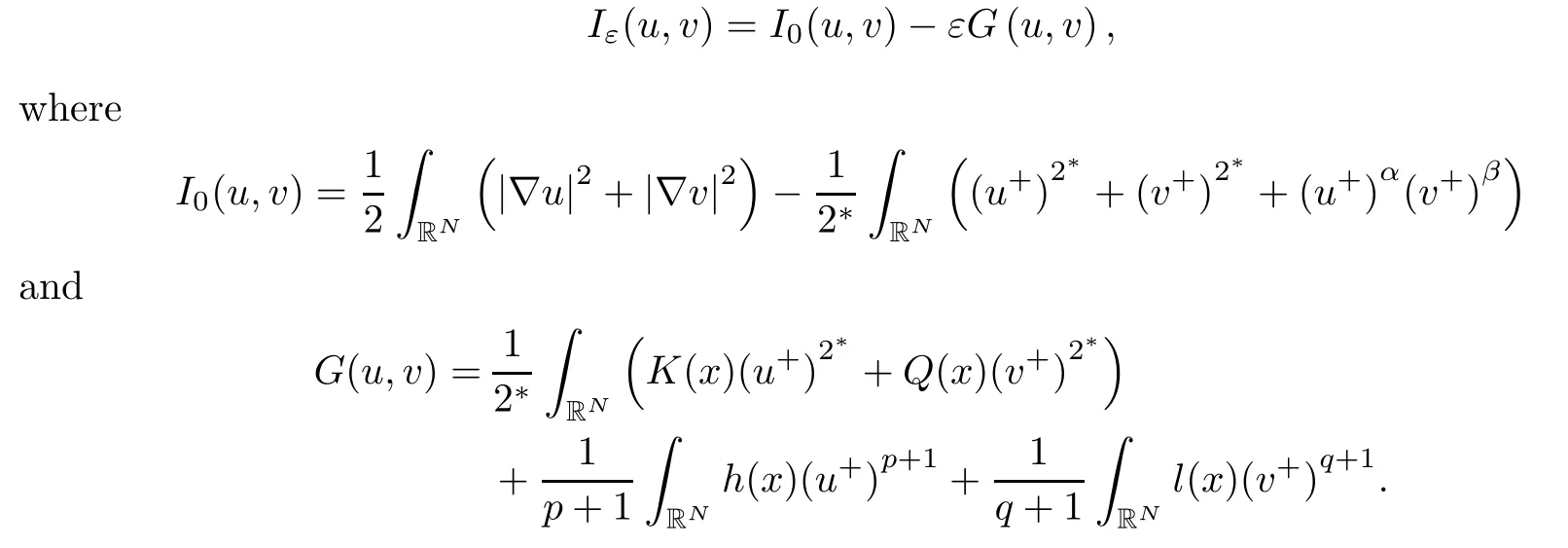
Here u±:=max{±u, 0}.
We will mention some results related to problem (1.1). As we know (e.g. [11–13]), the radial function
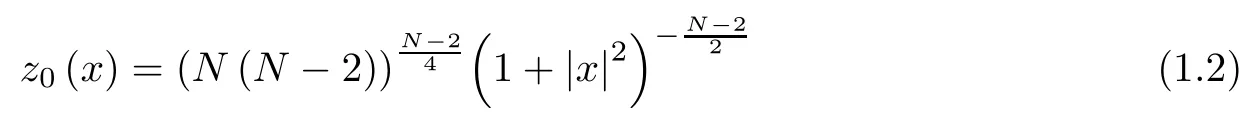
solves the problem

and zµ,ξachieves the best constant for the embeddingwhere zµ,ξis defined by
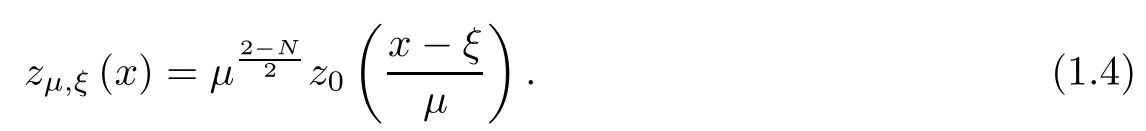
We denote
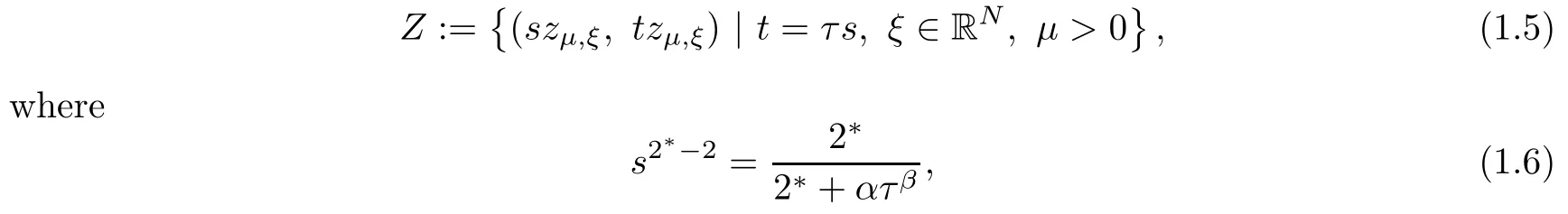
and τ is a solution of equation
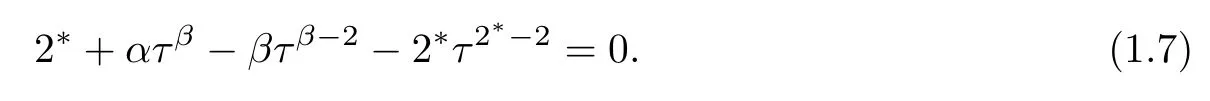
From[14],there exists at least one positive root to equation(1.7). More precisely,we have that
(A1) If 1< β <2, 1< α <2 andthen equation (1.7) has a unique positive root.
(A2) If 1< β <2 and α ≥ 2, then equation (1.7) has exactly two positive roots.
(A3) If β =2 and N =3,4,5, then equation (1.7) has a unique positive root.
(A4) If β > 2 and N = 4,5 or 4 < β < 5 and N = 3, then equation (1.7) has exactly two positive roots.
(A5) If 2< β ≤ 4 and N =3, then equation (1.7) has a unique positive root.
In particular, in this paper, we assume that α,β ≥ 2, N = 3, 4. Thus equation (1.7) has a unique positive root τ. Combining (1.5) with (1.6), we get that positive constants s, t and the manifold Z are uniquely determined.
In [15], Abdellaoui, Felli and Peral studied the following coupling system:
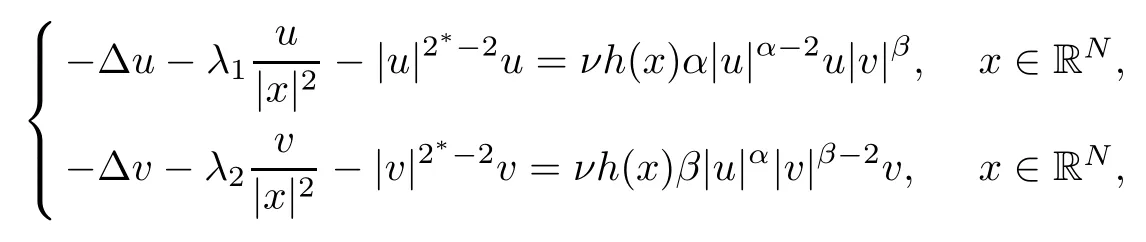
where λ1,λ2∈ (0,λN) and λNThey analyzed the behavior of (PS) sequence in order to recover compactness for some ranges of energy levels,and they proved the existence of a ground state solution. In [16], Chen and Zou studied following nonlinear Schrdinger system which is related to the Bose-Einstein condensate:
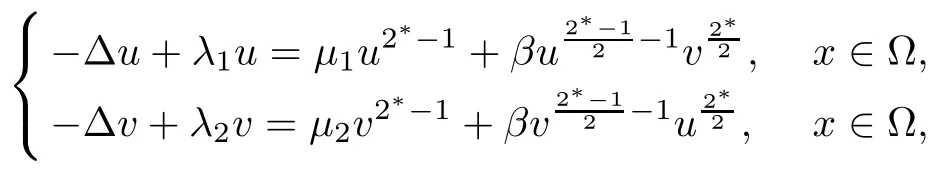
where Ω ⊂ RNis a smooth bounded domain. They proved the existence of positive least energy solutions when N ≥5. In [14], Peng,Peng and Wang considered the following coupling system with critical exponent:
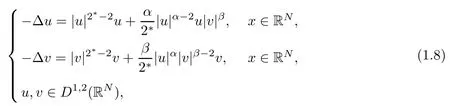
where α, β > 1, α + β = 2∗. They got a uniqueness result on the least energy solutions and showed that the manifold Z of the synchronized positive solutions is non-degenerate for some ranges of the parameters α,β,N.
A natural question is whether there are positive solutions to problem (1.1) which approximate (szµ,ξ, tzµ,ξ). The main difficulty is that the embeddingis not compact, so the (PS) sequence will fail to be compact. Motivated by [17, 18], we will adopt a perturbation argument and a finite dimensional reduction method to find positive solutions of problem (1.1).
More precisely, for the existence of positive solutions, we make the following assumptions:
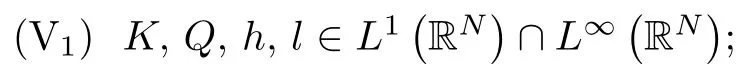
(V2) h, l are continuous functions and have compact supports;
(V3) K, Q ≤ 0 and K(x), Q(x)→ 0 as |x|→ ∞;
(V4) There exists ξ0such that h(ξ0), l(ξ0) > 0 and K(ξ0) = Q(ξ0) = 0. Moreover, we assume that there are positive constants a, b such that as x − ξ0→ 0, it holds that
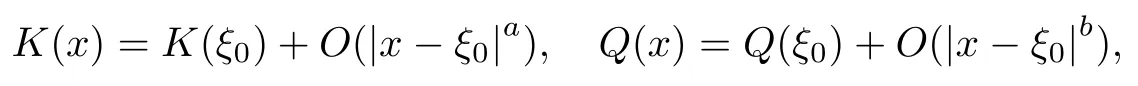
where (N +2)/2 ≤a, b Our main result in this paper can be stated as follows: Theorem 1.1Suppose that N =3 or 4,α, β ≥ 2 and(V1)–(V4)hold. Then there exists ε0> 0, µ∗> 0 and ξ∗∈ RNsuch that for all |ε| < ε0, problem (1.1) has a positive solution(uε,vε) with (uε,vε) → (szµ∗,ξ∗,tzµ∗,ξ∗) as ε → 0. In particular, if we suppose that K =Q ≡0, then we have Corollary 1.2Suppose that N = 3 or 4, α, β ≥ 2, (V1) and (V2) hold. If there exists ξ0such that h and l have the same sign at ξ0, then there exists ε0> 0, µ∗> 0 and ξ∗∈RNsuch that for all |ε| < ε0, problem (1.1) has a positive solution (uε,vε) with (uε,vε) →(szµ∗,ξ∗,tzµ∗,ξ∗) as ε → 0. In this section, we will give some lemmas which will be used to prove our main result. Lemma 2.1Z is a non-degenerate critical manifold of I0, in the sense that where TzZ is defined by the tangent space to Z at z. ProofFor proof, the reader can refer to Theorem 1.4 in [14]. Lemma 2.2Let z =(szµ,ξ,tzµ,ξ). Thenwhere I is the identity operator and C is a compact operator. ProofIt is easy to see that where ϕ =(ϕ1,ϕ2),ψ =(ψ1,ψ2), Suppose that {ϕn} is a bounded sequence in D1,2(RN). Then, Thus, it is sufficient to prove that Then we get On the other hand, for any E ⊂RN, we have that if |E| is small enough. Therefore, we apply the Vitali convergence theorem to get Next we will use a perturbation argument, developed in [19, 20], which permits us to find critical points of the C2functional 山药入土较深,播种行要深翻80-90 cm,这是山药获得优质高产的基础。一般单种山药按大小行栽培采取80 cm和60 cm的组合,若等行距栽培的,行距为70 cm。深翻松土采用机器进行,机器深松能一次性完成松土、开沟、培垄等多道工序,可大大提高劳动效率,减轻劳动强度,同时不打乱土层,使沟内土壤细碎疏松,适合山药生长。机械深松种出的山药直、圆、滑的程度大大超过人力深松耕的山药,极大地提高商品率。 near a manifold Z of critical points of I0under suitable non-degeneracy conditions. Since 0 < p, q < 1, G fails to be C2on D1,2RN× D1,2RN. To overcome this lack of regularity,we have to modify the abstract approach a little. First, it is convenient to work in the Banach space with the norm where zµ,ξhas been introduced in Section 1. R, µ1and µ2will be chosen later on. In any case,we shall take R in such a way that ω = ω1∪ ω2⊂ BR(0), ω1, ω2are the supports of h(x) and l(x), respectively. Denote where a depends on R, µ1and µ2. For (u,v)=z+w ∈U and |x| In particular, since ω ⊂ BR, it holds that then Φ ∈ L∞RN. Therefore, if we denote the solution Φ =JΨ, we have following results: Lemma 2.3If (V1) and (V2) are satisfied, then (JAε,JBε)(U)⊂ X. ProofFrom (V1) and (V2), it is not hard to see that for any (u,v)∈U, Lemma 2.4If (V1) and (V2) are satisfied, then (JAε,JBε)∈ C1(U,X) and where (ζ1,ζ2) is the unique weak solution of the problem ProofBy a direct calculation, it is not hard to verify that (JAε,JBε) is differentiable and that its Frechet derivative is given by (2.1)–(2.2). Let us now show that d(JAε,JBε) :U → L(X) is continuous. Indeed, let (u,v) ∈ U and (un, vn) ∈ U such that (un,vn) → (u,v)in X. Thus we have that Direct calculation yields that Since (un,vn)→(u,v) in X, we obtain that Moreover, by the Sobolev embedding inequality, we deduce that On the other hand, by the elliptic regularity, we have that By (2.4) and (2.5), we have that Thus the proof is complete. Remark 2.1When α =2 or β =2, it is easier to check the above result. Let TzZ =span{q1,··· ,qN+1} denote the tangent space to Z at z =(szµ,ξ,tzµ,ξ), where We now have the following significant lemma: Lemma 2.5Suppose that (V1) and (V2) hold. Then there exists ε0and a C1function such that for any µ1< µ < µ2, ξ ∈ BR(0) and ε ∈ (−ε0,ε0), we have that (i) (w1(µ,ξ,ε), (w2(µ,ξ,ε)) is orthogonal to TzZ; (ii) z+w(µ,ξ,ε)− J(Aε,Bε)(szµ,ξ+w1(µ,ξ,ε),tzµ,,ξ+w2(µ,ξ,ε))∈ TzZ; ProofLet where z =(szµ,ξ,tzµ,ξ), w =(w1,w2). We defineby where u=(u1,u2), v =(v1,v2). From Lemma 2.4, it follows that H is of class C1and that its derivative with respect to variables (w,σ) is given by where φ =(φ1,φ2)∈ HRN, d=(d1,··· ,dN+1)∈ RN+1. For any z ∈ Z0, and its derivative at z ∈ Z0, ε=0, σ =0 and w =0 is as follows From Lemma 2.2, we can see thatand that it is a Fredholm operator of index 0. On the other hand,is injective, since Z is a nondegenerate manifold of I0. Thus,is invertible. Finally, it is easy to get our result by using the Implicit Function Theorem; for details see [19]. From Lemma 2.5, it is natural to introduce the perturbed manifold which is a natural constraint for Iε; namely, if u ∈ Zεand In fact, if zεis a critical point of Iεconstrained on Zε, then we have that On the other hand, from Lemma 2.5 (ii) we have that Moreover, we have that Consequently, if z is a critical point of the restriction G|Z, which is a proper local minimum or maximum point, then z+w(µ,ξ,ε) turns out to be a critical point of Iε. From the above analysis,the search for solutions to problem(1.1)is reduced to the search for the local minimum or maximum point of the finite dimensional functional on (µ1,µ2)× BR(0). In order to simplify the functional, we denote In this section, we will solve the finite dimensional problem. Before proving our result, we give some important lemmas. Lemma 3.1Assume that K ∈L1(RN)∩L∞(RN) and K(x)→0 as |x|→∞. Then, ProofIf µ → 0 and |ξ|→ ∞, then Note that Thus, by the Dominated Convergence Theorem, we have proven the result. where R>0, I1and I2are defined by By a direct calculation, we obtain that Thus, for given δ > 0, by K ∈ L1(RN), we take R large enough such that |I2| < δ. On the other hand, It is not hard to see that the last integral tends to 0. Therefore, we have proven the result. Lemma 3.2Suppose that N = 3 or 4,and h is a continuous function with compact support. Then we have that (i) Φ(µ,ξ)=O(µγ) as µ → 0+; (iii) If h(ξ0)>0, then there exists a positive constant C such that Proof(i) Let r >0 be such that ω1∈ Br(0). Assume first that|ξ|≥ 2r. If|x| On the other hand, if |ξ|<2r, then we have that where ωN−1is the surface area of the N − 1 dimensional unit ball and BR(x) is the ball with center x, radius R>0. The last inequality is due to N − 2γ − 1> −1 when N =3 or 4. Thus we have proved (i). Therefore there exists a positive constant C such that Lemma 3.3Suppose that N =3 or 4 and (V1)–(V4) hold. Then we have that (iii) There exists µ0>0 such that Proof(i) From (V1), (V2) and Lemma 3.2 (i), we have that Thus the result directly follows from (V3) and (3.1). (ii) From (V1)–(V3), Lemma 3.1 and Lemma 3.2 (ii), it is easy to get that (iii) Since there exists a positive constant C such that Hence, from (V3) and (3.2), we get that Similarly, there exists a positive constant C2such that From Lemma 3.2 (iii), there exists a positive constant C3such that Similarly, there exists a positive constant C4such that Thus, from (3.3), (3.4), (3.5) and (3.6), we have that On the other hand, since Therefore, it is possible to choose µ0>0 small and a constant C5>0 such that Proof of Theorem 1.1By (ii) of Lemma 3.3, there exist a large µ2> 0 and R2> R such that On the other hand, from Lemma 3.3 (ii) we can find a small µ1>0 such that In correspondence with µ1,µ2and R=R2, we fix Z0. From (3.7) and (3.8), it follows that is achieved at some (µ∗,ξ∗), and the perturbation argument allows us to conclude that is a critical point of Iε. Thus we have that Then multiplying the first equation bythe second equation byand integrating by parts,we findHence (uε,vε) are nonnegative solutions of problem (1.1). Finally, the strong maximum principle implies that uε, vε>0. Remark 3.1Our assumptions (V3) and (V4) may be replaced by the following: where (N +2)/2 ≤a, b In fact, by a similar method, we can get a negative minimum point ofwhich gives rise to a solution to problem (1.1). AcknowledgementsThe author would like to thank Prof. Shuangjie Peng for stimulating discussions and helpful suggestions on the present paper.2 Preliminary Results

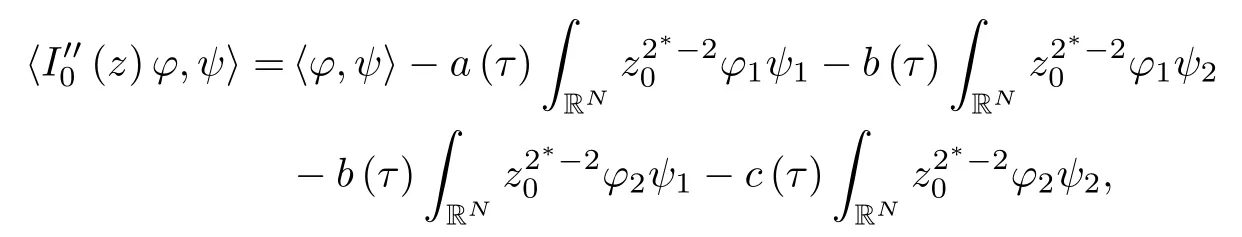
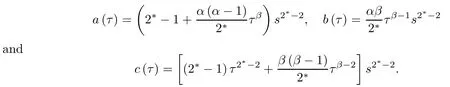
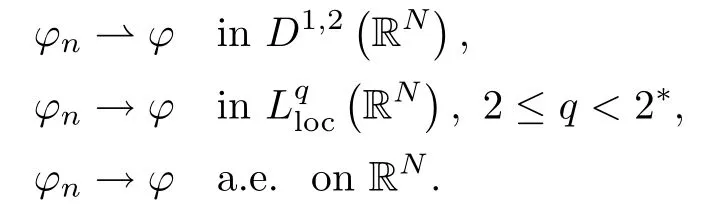
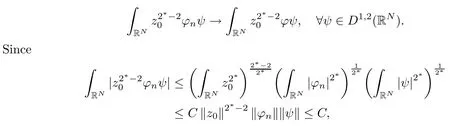
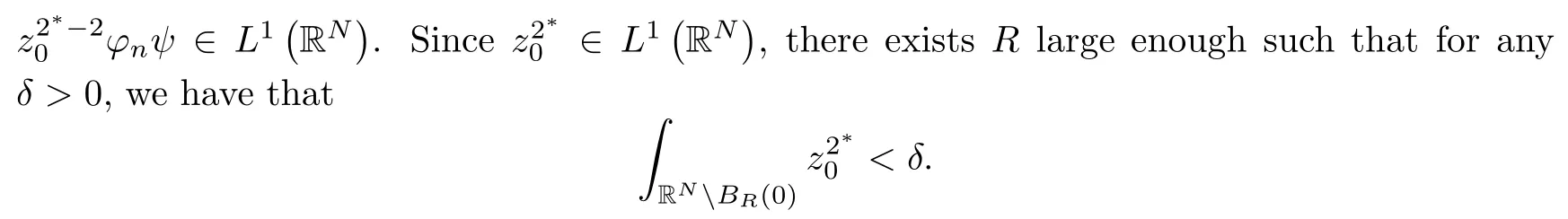
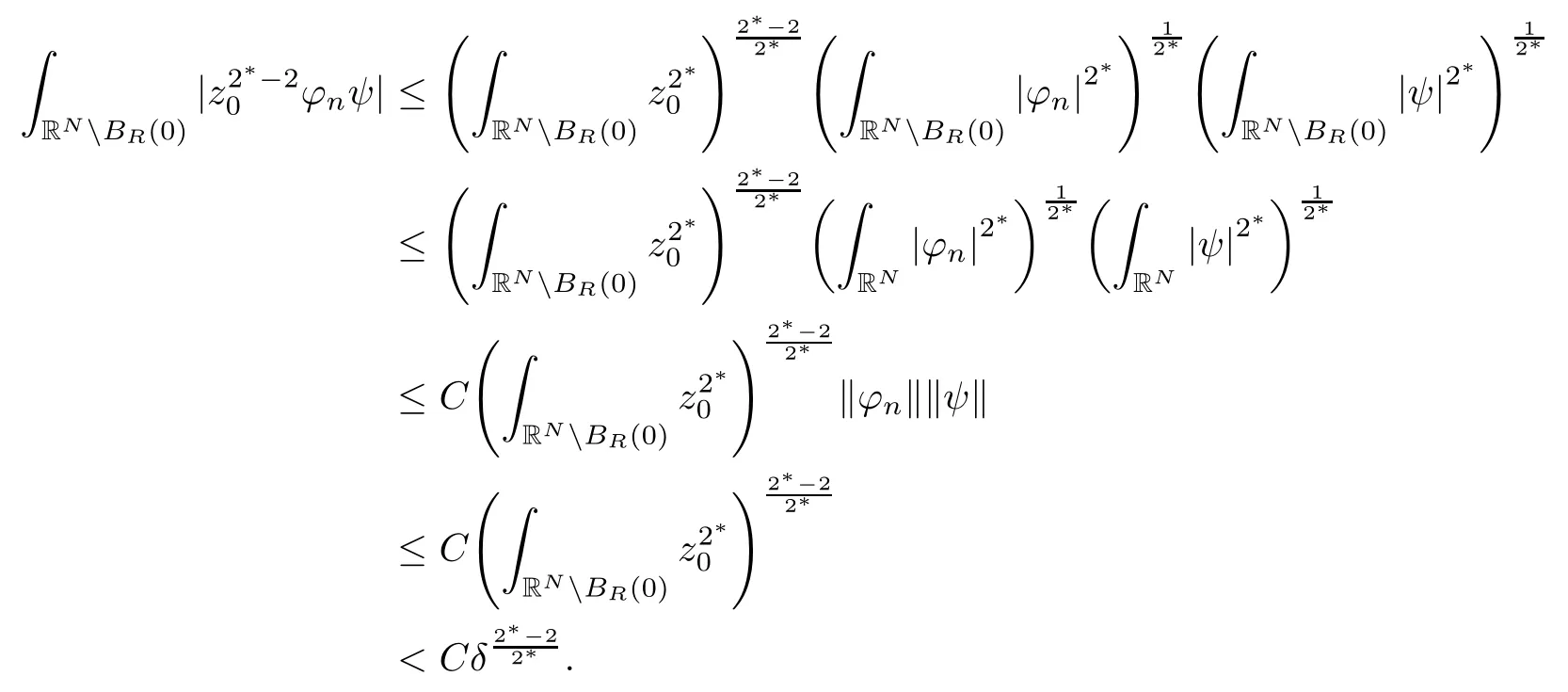
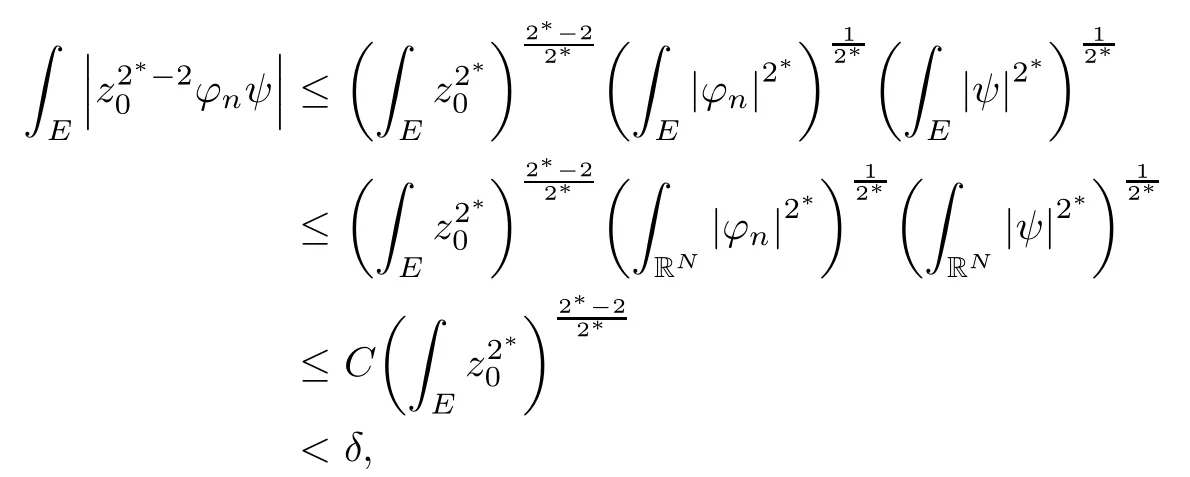



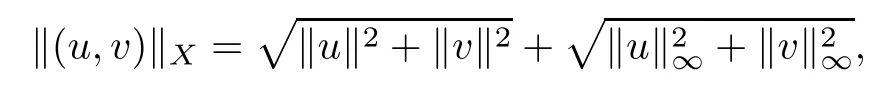
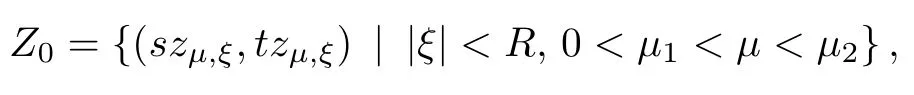
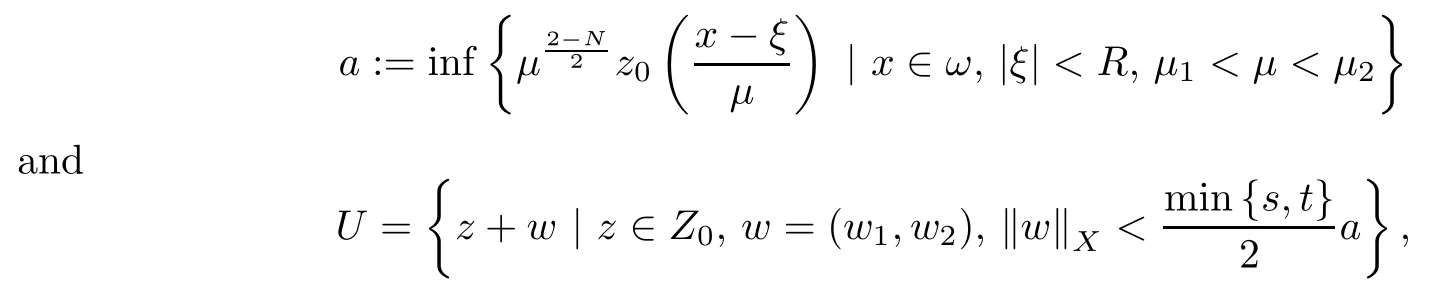
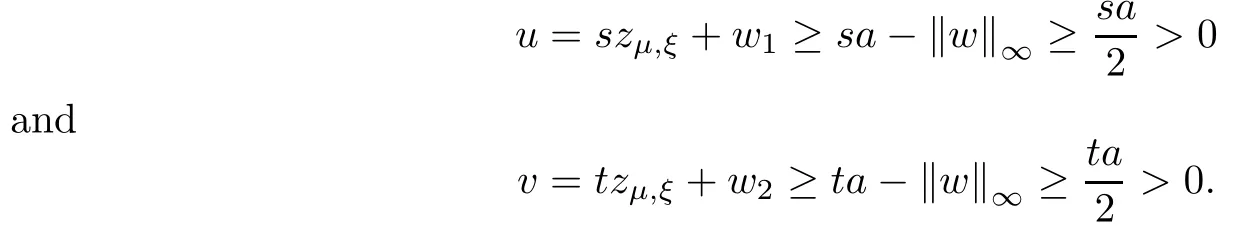
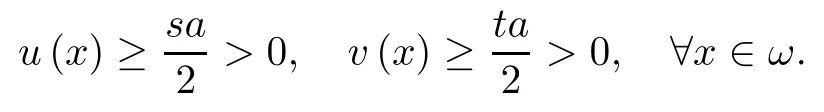
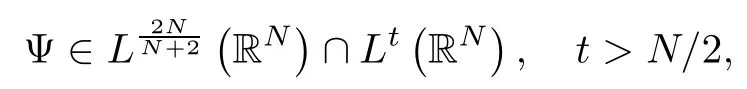
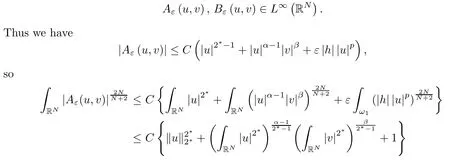
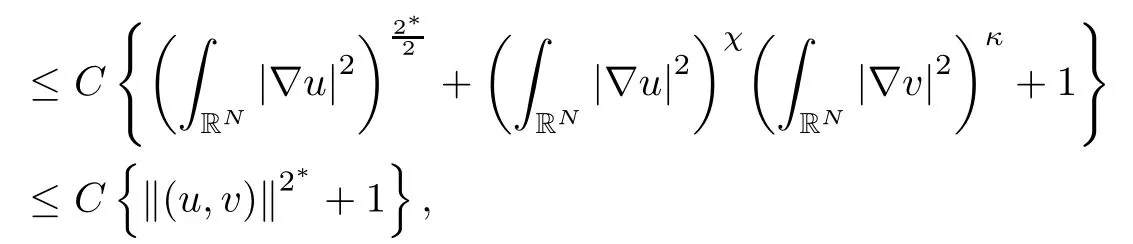
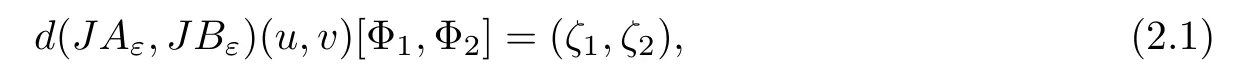
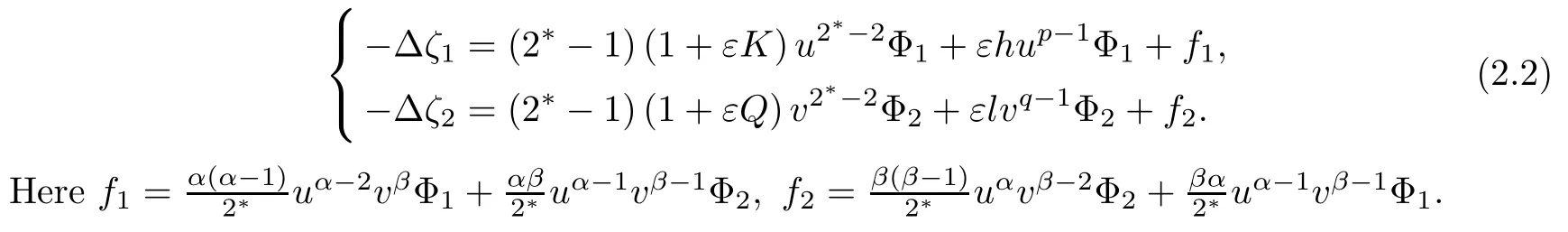
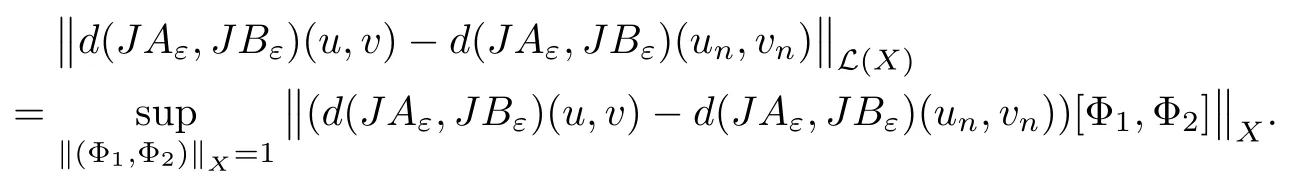

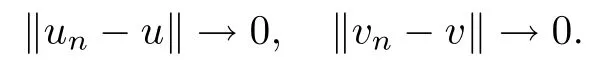
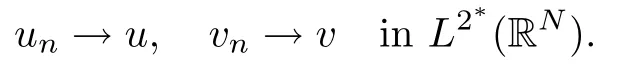

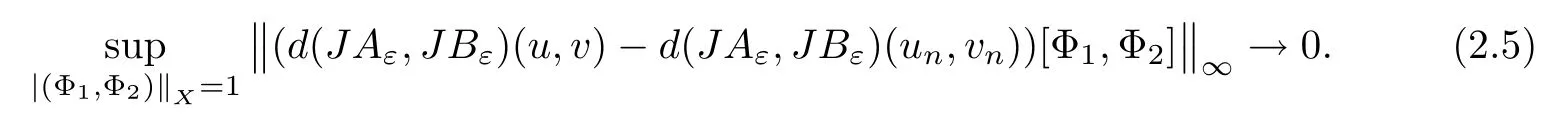
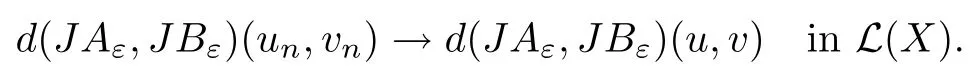
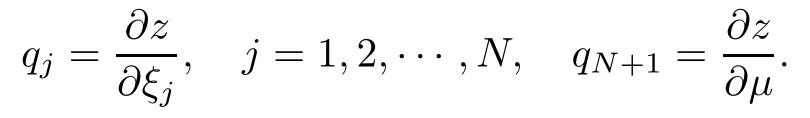
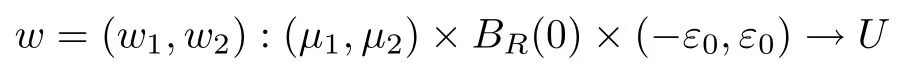

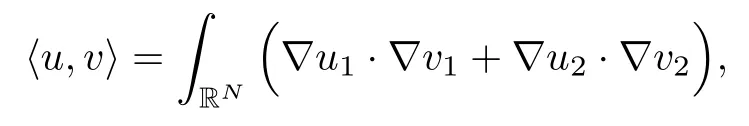
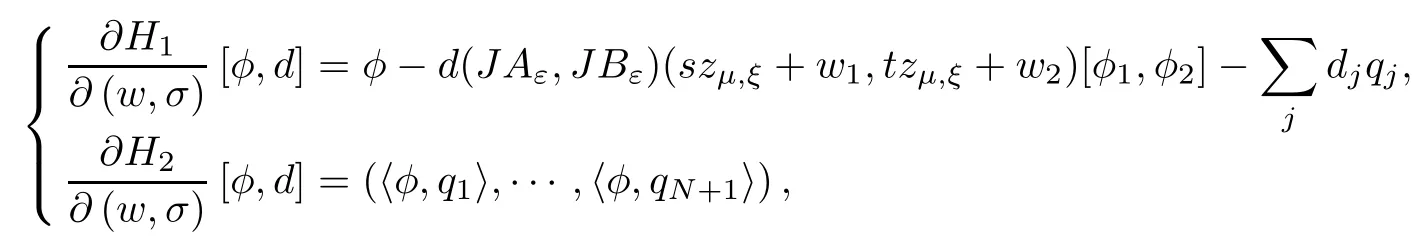
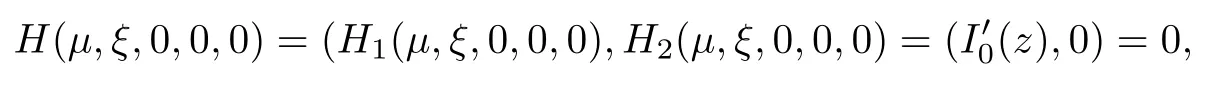
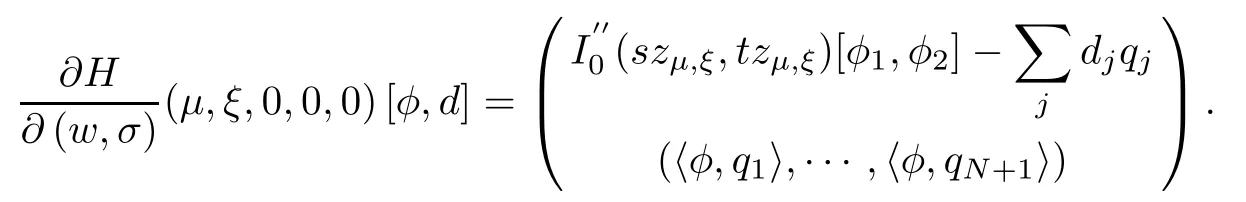
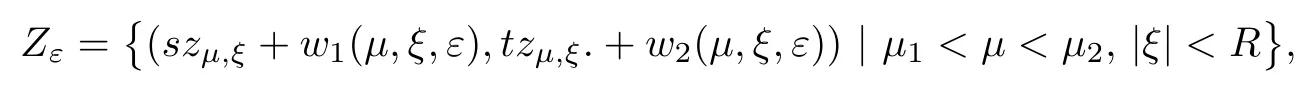
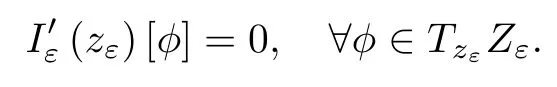


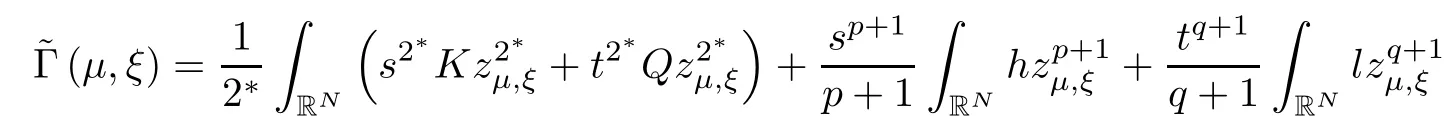
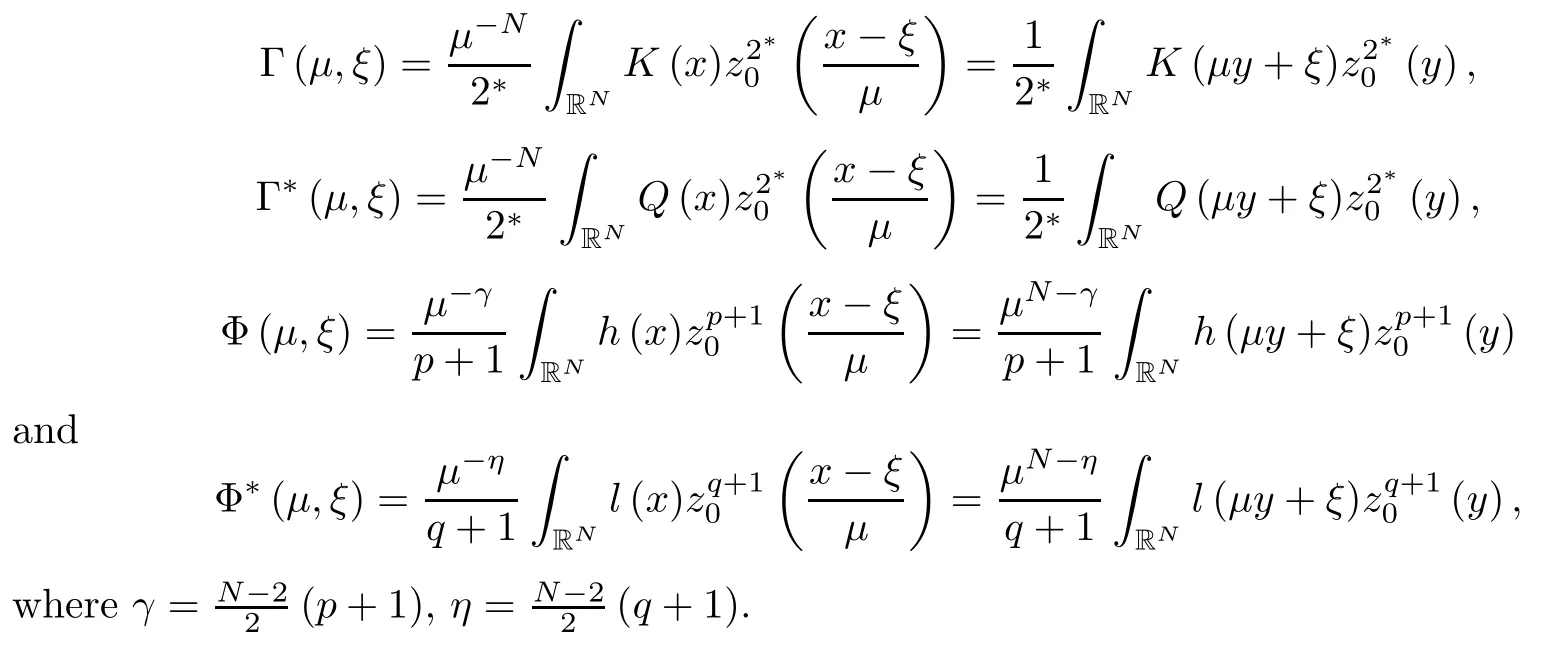
3 Proof of the Main Result
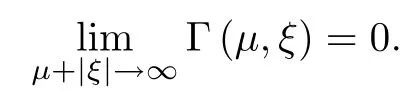
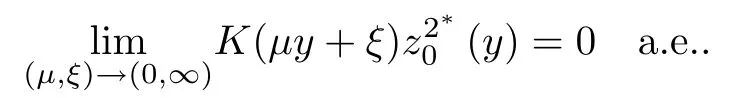
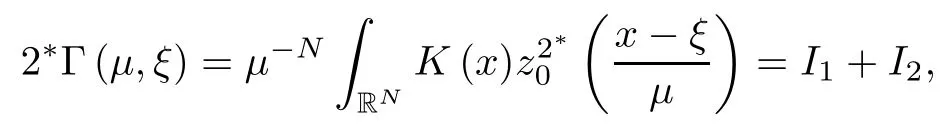
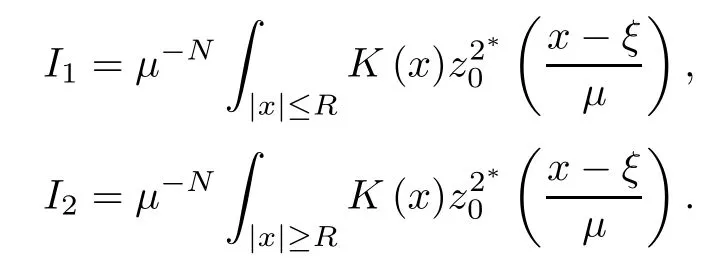
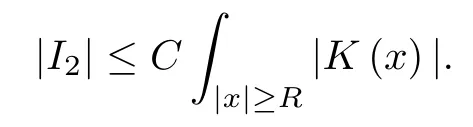
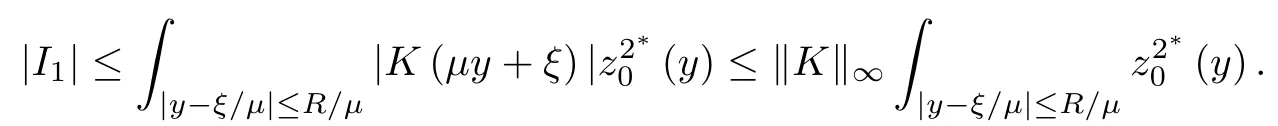

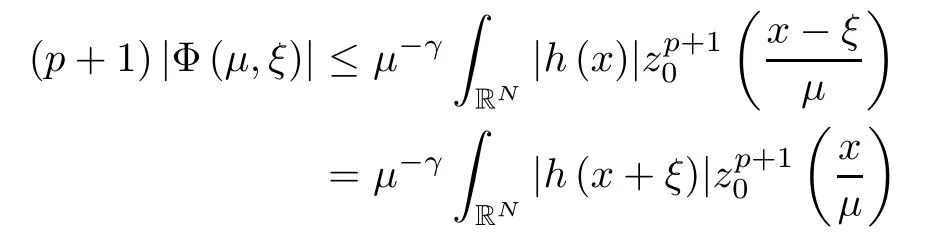
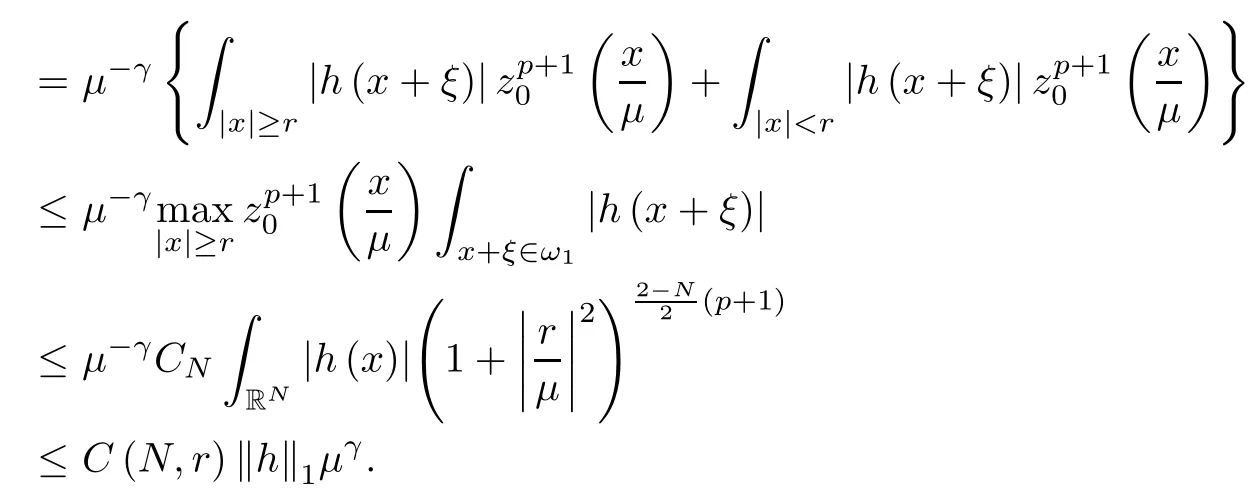
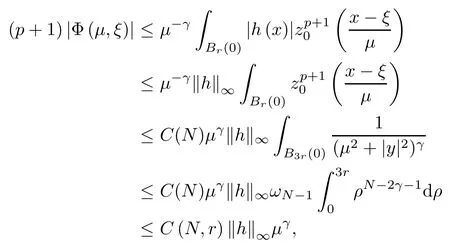
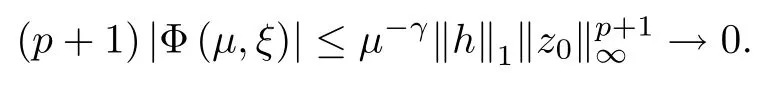
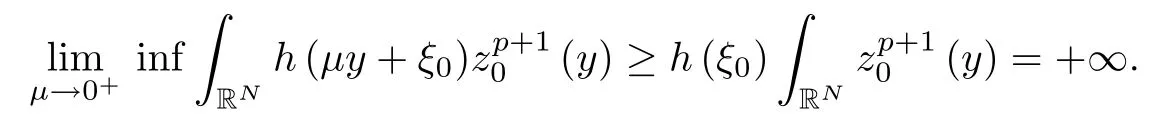
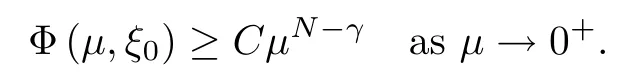
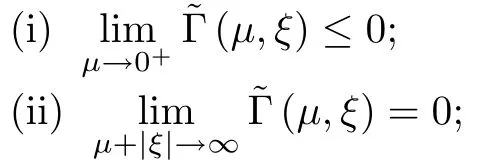
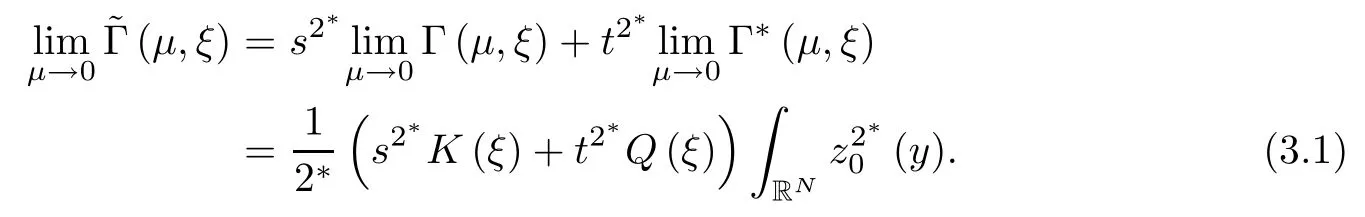
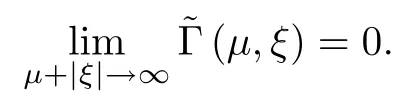
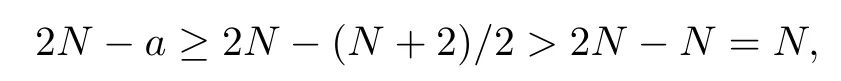

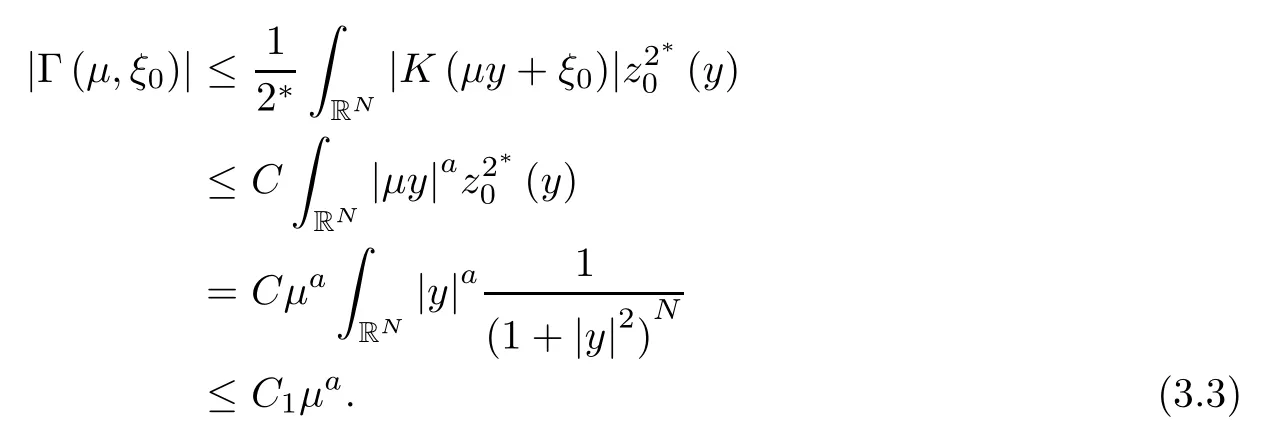




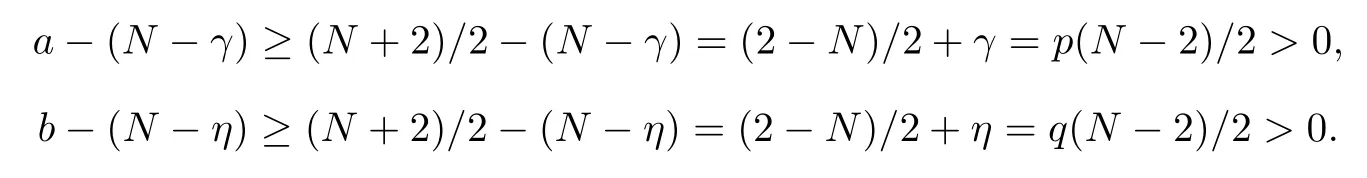

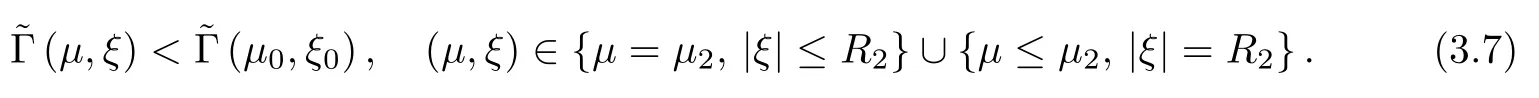
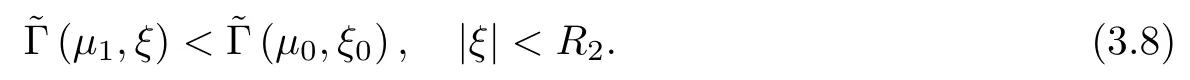

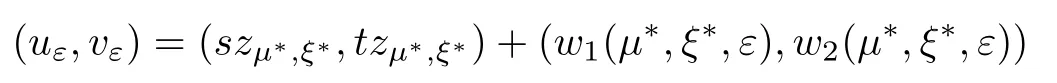

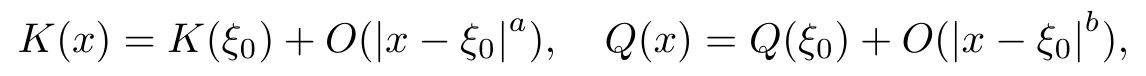
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ON BOUNDEDNESS PROPERTY OF SINGULAR INTEGRAL OPERATORS ASSOCIATED TO A SCHRDINGER OPERATOR IN A GENERALIZED MORREY SPACE AND APPLICATIONS∗
- GLOBAL WEAK SOLUTIONS FOR A NONLINEAR HYPERBOLIC SYSTEM*
- ASYMPTOTIC STABILITY OF A VISCOUS CONTACT WAVE FOR THE NE-DIMSIAL CPBL VK QU G X*
- BOUNDEDNESS OF VARIATION OPERATORS ASSOCIATED WITH THE HEAT SEMIGROUP GENERATED BY HIGH ORDER SCHRDINGER TYPE OPERATORS∗
- THE EXISTENCE OF A BOUNDED INVARIANT REGION FOR COMPRESSIBLE EULER EQUATIONS IN DIFFERENT GAS STATES*
- THE DAVIES METHOD FOR HEAT KERNEL UPPER BOUNDS OF NON-LOCAL DIRICHLET FORMS ON ULTRA-METRIC SPACES∗
