双向可逆类和刹车类问题的从容应对

安徽 邵 永

高等教育出版社出版的《普通高等学校招生全国统一考试大纲的说明》中明确指出：高考物理试题着重考查考生的知识、能力和科学素养，注重理论联系实际，注意物理与科学技术、社会和经济发展的联系，注意物理知识在生产、生活等方面的广泛应用。运动学的试题往往以生活、生产实际为情景，情景中包含单个或多个研究对象，各对象参与单个或多个过程，且各对象、各过程间相互作用、相互牵连、相互影响。这类问题往往具有条件隐蔽、过程复杂的特点，能训练学生的科学思维。在运动学中双向可逆类和刹车类问题是高考常考的内容，对这两类问题学生经常由于计算繁琐出现错解、漏解等现象，我们可以利用基本知识、基本方法和基本思想，另辟蹊径优化分析、简化运算，降低试题难度，做到学以致用、培养能力、落实学科核心素养。下面通过几道例题体会如何对这两类问题从容应对。

一、双向可逆类问题

【例1】一物体在光滑水平面上，由静止开始在水平恒力F1作用下运动t秒，t秒末换上大小为F2的水平恒力，物体又经过2t秒回到出发点，在此过程中物体受到F1、F2的比值为

( )

【解法一】分段法

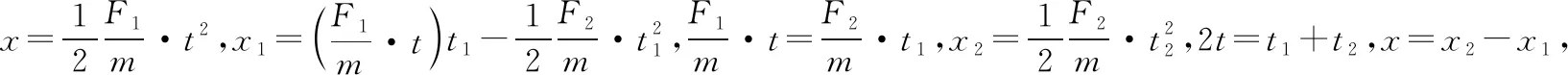
【解法二】全程法

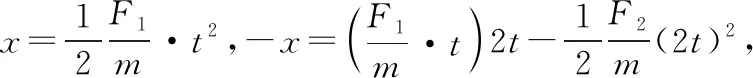
【点拨】由于物体在F2作用下的正向减速和反向加速运动过程中加速度不变，由逆向思维反向加速运动可以看出正向的减速运动，因此可以把这两过程看成一个过程，从上面的解析可以看出：利用全程法既简化了过程分析又降低了运算难度，提高了分析问题解决问题的效率。由于很多矢量方向不同，所以使用全程法时一定要先规定正方向，用规定的正方向描述各物理量的正负。

二、刹车类问题

【例2】在铁路与公路交叉点上，由于司机粗心、判断失误或车况等原因常常发生交通事故。现有一辆长为5 m的汽车以v1=15 m/s的速度行驶，在离铁路与公路交叉点175 m处，汽车司机突然发现离交叉点200 m处有一列长300 m的列车以v2=20 m/s的速度行驶过来，为了避免事故的发生，求：

(1)汽车司机如果立刻做匀加速运动，则最小加速度应为多大？

(2)汽车司机如果立刻刹车做匀减速运动，则最小加速度为多少？

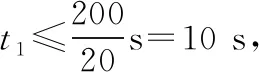
(2)方法一 常规解法

方法二 应用平均速度公式明确运动情景

【点拨】汽车的减速运动是典型的刹车类问题，一旦速度减为零将停止运动，不会做反向加速运动。在上述解法一中，先根据双向可逆类的公式进行计算，通过验证得到汽车正在做反向加速运动，此解虽然有一定的物理意义但不符合实际情景，属于“增根”应该舍去，然后在提前减速到停止的前提下再次计算，在解题过程中如果不验证就会产生错解，验证后发现问题换另外一种情况再求解太麻烦，并且解法中对为什么在提前减速到停止的情况下计算没做交代，而实际上学生对这一点不理解者居多。在解法二中，先用平均速度公式判断正确的运动情景，然后在汽车先减速到停止的情况下进行计算，可以做到既清晰明了又严谨规范。

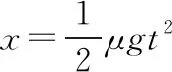
【例3】(2019年全国卷Ⅱ)一质量为m=2 000 kg的汽车以某一速度在平直公路上匀速行驶。行驶过程中，司机忽然发现前方100 m处有一警示牌，立即刹车。刹车过程中，汽车所受阻力大小随时间变化可简化为图1(a)中的图线。图1(a)中，0～t1时间段为从司机发现警示牌到采取措施的反应时间(这段时间内汽车所受阻力已忽略，汽车仍保持匀速行驶)，t1=0.8 s；t1～t2时间段为刹车系统的启动时间，t2=1.3 s；从t2时刻开始汽车的刹车系统稳定工作，直至汽车停止，已知从t2时刻开始，汽车第1 s内的位移为24 m，第4 s内的位移为1 m。

(1)在图1(b)中定性画出从司机发现警示牌到刹车系统稳定工作后汽车运动的v-t图线；

(2)求t2时刻汽车的速度大小及此后的加速度大小；

(3)求刹车前汽车匀速行驶时的速度大小及t1～t2时间内汽车克服阻力做的功；司机发现警示牌到汽车停止，汽车行驶的距离约为多少(以t1～t2时间段始末速度的算术平均值替代这段时间内汽车的平均速度)？

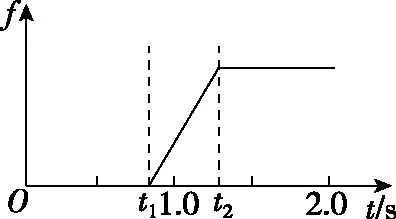
a

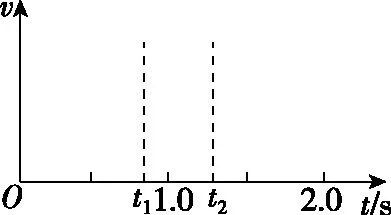
b

【解析】(1)v-t图象如图2所示。

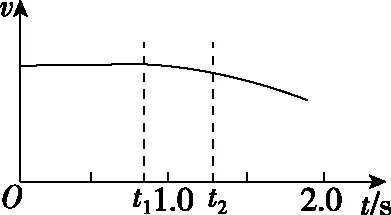
图2

(2)方法一 常规的分类讨论法

设刹车前汽车匀速行驶时的速度大小为v1，则t1时刻的速度也为v1，t2时刻的速度为v2，在t2时刻后汽车做匀减速运动，设其加速度大小为a。

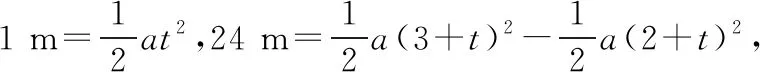
方法二 应用初速度为零的匀变速直线运动规律明确运动情景

在初速度为零的匀加速直线运动中第(n+1) s和第(n+4) s内位移之比为

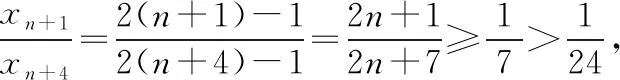
设第4 s内物体运动了ts，则

联立解得a=8 m/s2，t=0.5 s

所以v2=a(t+3)=28 m/s

(3)设汽车的刹车系统稳定工作时，汽车所受阻力的大小为f1，由牛顿第二定律有f1=ma

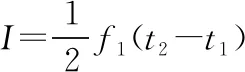
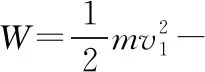
【点拨】本题是2019年全国卷Ⅱ的压轴题，设置符合压轴题的特点，既有复杂的情景又有复杂的运算，学生做起来费时费力。虽然上述的解法一对高考题中提供的参考答案做了调整，可解法仍然非常烦琐，但在解法二中，如果利用逆向思维结合初速度为零的匀变速直线运动规律判断出汽车在第4 s的某时刻已经停止运动，在具体的情境下进行计算，清晰明了，运算量不大，省力省时又事半功倍。利用这样的方式降低本题难度在我们平时教学和学习中是有所体现的，如我们在自由落体运动的频闪照片中分析拍下第一张图片时小球的速度是否为零，平抛运动的频闪照片中分析拍下第一张图片时小球是否在抛出点就是利用初速度为零的匀变速直线运动规律进行判断的。

【小结】物理是一门综合性很强的学科。特别是对于多情景的物理问题，学生不是无从下手，就是解题不全面、不规范、不严谨，或者是出现增根发现不了。如果我们利用逆向思维、平均速度公式、初速度为零的匀变速直线运动规律等基本思想、基本知识和基本方法，另辟蹊径明确定物体的具体运动情景，这样就可以大大降低试题难度、优化分析、简化运算、起到事半功倍的效果。

三、斜面中的类刹车类问题和双向但不可逆类问题

【例4】(2018年浙江理综改编)可爱的企鹅喜欢在冰面上玩耍，别看企鹅在陆地冰雪上肥胖笨拙，一旦入水则完全不同，骁勇得让你瞠目结舌，真可谓是游泳健将。有一企鹅从水中以10 m/s的速度冲上倾角为30°的倾斜冰面上，卧倒以肚皮贴着冰面向前滑行。

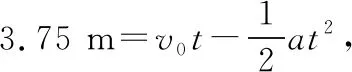
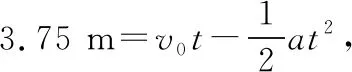
【点拨】物体沿斜面向上做减速运动也有速度减为零的情况，不同于物体在水平面上运动，当物体速度减为零后在重力的作用下物体仍然有滑下的可能性，物体能否滑下来取决于μ和tanθ的大小关系，如果μ≥tanθ，物体会静止在最高点，这属于类刹车类问题；如果μ