卷积神经网络并行方法研究

朱传家 刘 鑫* 方佳瑞

1(江南计算技术研究所 江苏 无锡 214083) 2(清华大学计算机科学与技术系 北京 100084)

0 引 言

随着深度神经网络的发展，深度学习技术广泛应用于语音识别[1]、图像识别[2]、自然语言处理[3]等领域。深度神经网络的成功源于深度神经网络模型具有从大量数据中学习复杂特征的能力。越来越大的数据集和网络模型可以提高训练的性能。然而，随着数据规模的增长和深度神经网络模型日益复杂，训练时间越来越长，训练需要的内存越来越多。提高深度神经网络的训练效率成为一大挑战。

深度神经网络模型种类繁多，不同的网络模型具有不同的特点。对不同的神经网络模型需要采用不同的并行优化方法。在一些卷积神经网络模型中，卷积层持有约10%的参数量和约90%的计算量，而全连接层持有约90%的参数量和约10%的计算量。因此，可以对卷积层采用数据并行的并行方法，对全连接层采用模型并行的并行方法。

本文基于国产超级计算机系统和深度学习框架Caffe[4]，对卷积神经网络进行并行方法研究，提出一种对卷积层使用数据并行、对全连接层使用模型并行的并行方法。

1 背景介绍

1.1 卷积神经网络基础

卷积神经网络是经典的深度学习网络，主要由卷积层、全连接层等组成。卷积层是卷积神经网络的核心，用于从输入层或较低层级的特征图中进行特征提取；全连接层的作用为连接所有的特征，将输出值送给分类器进行输出，如图1所示。

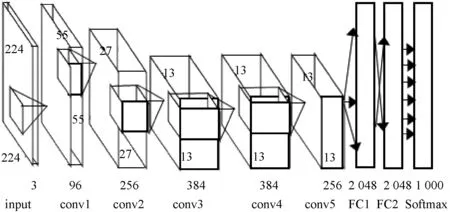
图1 AlexNet网络结构图[5]

训练卷积神经网络使用反向传播算法对网络参数进行优化。反向传播算法包括正向计算和反向计算。正向计算顺着网络结构依次计算，最终得到网络的输出结果；反向计算计算损失函数相对于网络参数权重的梯度，并利用梯度更新网络参数。基于同步的随机梯度下降算法[6]具有结构简单、收敛性好的优点，广泛应用于网络参数优化。分布式系统中使用分布式随机梯度下降算法，在不同的工作节点间进行梯度的归约和平均，公式如下：

Wt+1=Wt-ηE(ΔWt)

(1)

式中：Wt为第t次迭代的权重值；η为学习率；ΔWt为第t次迭代W关于损失函数的梯度；E(ΔWt)为第t次迭代各节点W关于损失函数的梯度的均值。

1.2 Caffe简介

Caffe[7]是加州大学伯克利视觉和学习中心(BVLC)推出的一款深度学习框架，广泛应用于工业界。它完全基于C++开发，具有结构清晰、层次分明、效率高和可移植性好的优点；采用模块化架构，易于扩展新的数据格式、网络层和损失函数等。

Caffe框架由Solver、Net、Layer和Blob定义[8]。Solver是求解器，负责协调模型的优化和测试；Net、Layer和Blob组成具体的模型。Net是网络，从下到上逐层定义整个模型，一次迭代可以看作Net的一次正向传播和反向传播。Layer是计算的基本单元，定义具体的运算，比如卷积、池化、全连接等。Blob是Caffe的标准数据结构，提供了统一的内存接口。

运行于国产超级计算机系统的Caffe不仅实现了应用程序的移植，还针对国产超级计算机系统的体系结构进行了深度优化，使用了专门开发的数学库[9]。Caffe继承了BVLC版Caffe的优点，并且在国产超级计算机系统上具有运行效率高、可进行大规模分布式扩展的优点。

2 相关工作

随着深度学习技术的发展，出现了很多深度神经网络并行方法的研究。常见的并行方法有数据并行和模型并行。数据并行[10]方法中，每台机器在小批量的数据上训练网络并计算梯度，采用同步或异步方式对网络参数进行同步；模型并行[11]方法中，将计算进行划分并分配到不同的机器上。

Google的DistBelief[12]和微软的Adams[13]都使用了数据并行和模型并行训练大规模模型。Coates等[14]提出了基于GPU集群的模型并行系统，Li等[15]提出了基于异步交互的参数服务器方式的数据并行。

然而，现有的对深度神经网络进行数据并行和模型并行方法的研究大多基于商用平台如GPU等，与国产超级计算机系统的体系结构相比具有比较大的差异。因此，针对国产超级计算机系统，本文研究并提出一种适合卷积神经网络的并行方法。

3 算法设计

对卷积层进行数据并行，对全连接层进行模型并行。图2展示了一个含有3个卷积层和2个全连接层的卷积神经网络，4个计算单元(进程)。卷积层的所有参数在每个计算单元上均有一个副本，全连接层的网络参数按照计算单元数进行切分,并按顺序分布在不同的计算单元上。

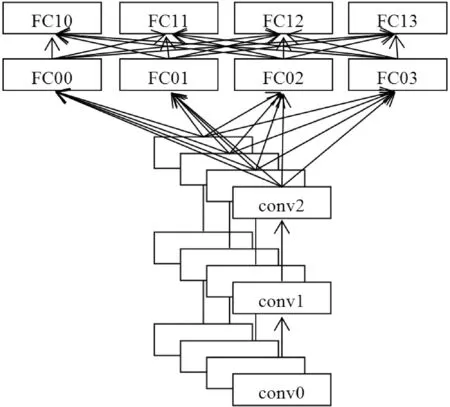
图2 卷积神经网络并行方法示意图

一次训练迭代优化过程包括前向传播过程和后向传播过程。前向传播过程中，卷积层利用计算单元持有的全部网络参数和输入数据计算预测输出。全连接层利用计算单元持有的部分网络参数和所有的计算单元的数据进行计算，得到部分预测输出，所有计算单元的预测输出进行整合后再按顺序分配到计算单元上。后向传播过程中全连接层对预测输出进行反向整合，再计算梯度并对梯度信息进行整合；卷积层正常计算梯度。最后，对每层的梯度信息采用同步随机梯度下降算法进行更新。

3.1 卷积层数据并行

卷积层数据并行采用去中心化的系统架构。去中心化的系统架构由多个工作节点组成，每个工作节点拥有相同的网络参数，自主进行参数更新，如图3所示。在每次优化迭代过程中，每个工作节点在网络正向传播过程中计算损失；在反向传播过程中计算梯度信息，并对梯度信息进行聚集平均操作，利用得到的梯度信息自主进行参数更新。

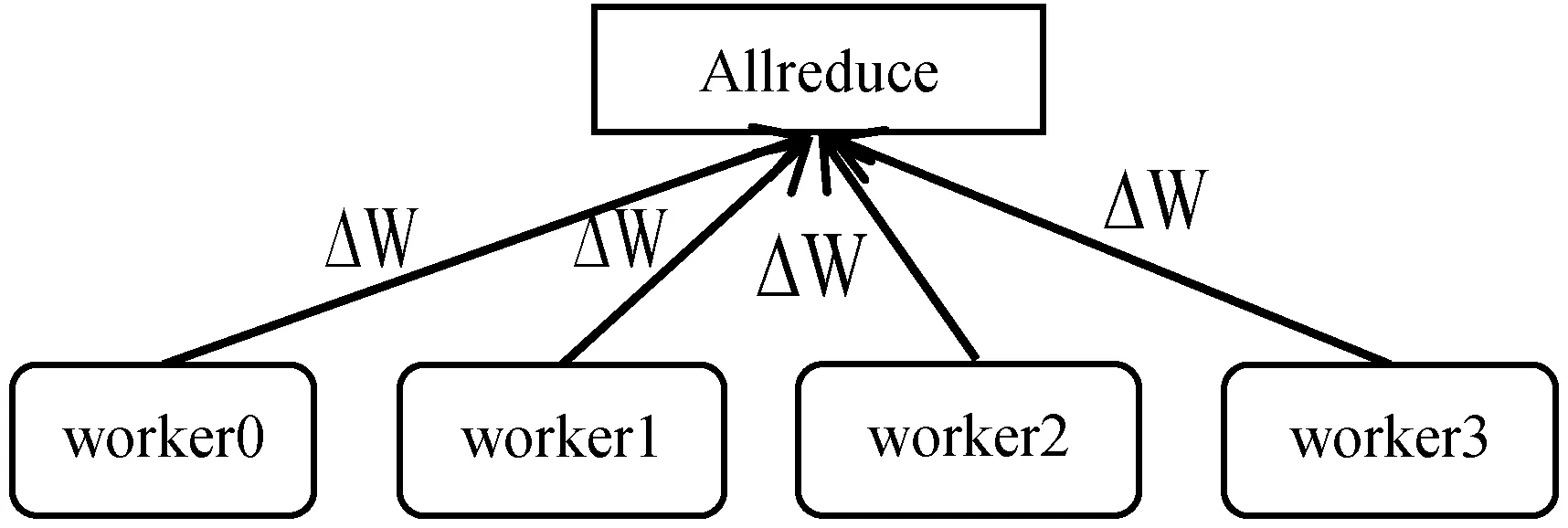
图3 去中心化方式数据并行架构图

去中心化数据并行方法的算法设计如下：

1) 网络初始化时：

所有工作节点同步卷积层的网络参数。

2) 在每次优化迭代过程中：

(1) 工作节点从下向上对卷积层进行特征计算；

(2) 工作节点从上向下对卷积层计算权重梯度、偏差梯度和数据梯度；

(3) 所有网络层梯度计算完成后，所有工作节点对权重梯度信息和偏差梯度信息进行聚集平均操作，使所有进程持有相同的梯度信息；

(4) 所有工作节点利用更新后的梯度信息自主更新网络参数。

3.2 全连接层模型并行

约定网络自下而上进行正向传播，自上而下进行反向传播。如图4所示，正向计算时，layer_i的输出top_data为layer_i+1的输入bottom_data；反向计算时，layer_i+1的输出bottom_diff为layer_i的输入top_diff。layer_i持有该层的权重weight、权重梯度weight_diff、偏差bias_data、偏差权重bias_weight和偏差权重梯度bias_diff。

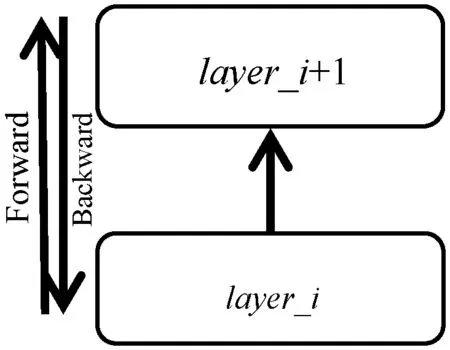
图4 网络层数据结构说明图

1) 网络层参数切分。全连接层模型并行时，对网络参数按照输出维度进行切分，需要切分的网络参数有网络权重、权重梯度、偏差权重、偏差权重梯度等。由于工作节点的计算能力均衡，因此选择等量切分方式。在正向特征计算中，每个工作节点的数据需要所有工作节点的网络参数才能计算出其相应的特征输出；在反向梯度计算中，每个工作节点需要所有工作节点的数据才能计算出其相应的梯度信息。

2) 正向传播过程。单节点全连接层正向传播时，特征输入bottom_data和权重weight的乘积加上偏差bias_data和偏差权重bias_weight的乘积为特征输出top_data。模型并行时，weight、bias_data、bias_weight切分后分布在不同的工作节点上，每个工作节点持有自己的bottom_data。以四个工作节点为例，进程号分别为0、1、2、3;相对应的数据结构为xx_0、xx_1、xx_2、xx_3。如2号进程的特征输入为bottom_data_2。

具体算法如下：

(1) 所有工作节点向其他工作节点广播自己的bottom_data_x，工作节点收到其他工作节点的bottom_data后按顺序进行拼接，如图5所示。

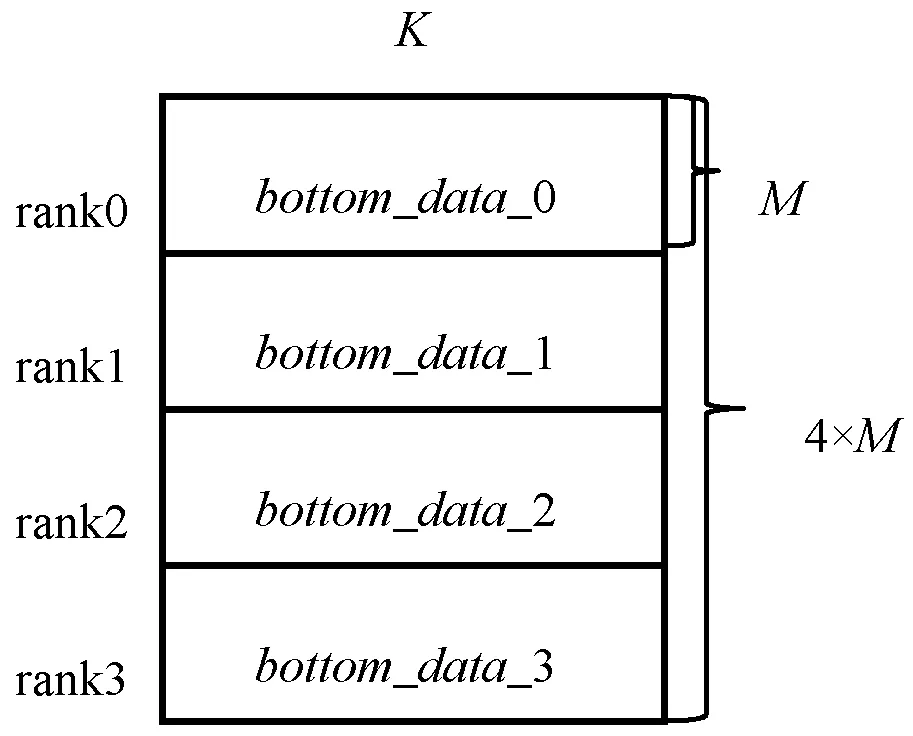
图5 bottom_data输入拼接图

(2) 所有工作节点使用拼接后的bottom_data和其持有的weight、bias_data进行计算，得到top_data_x，如图6所示。

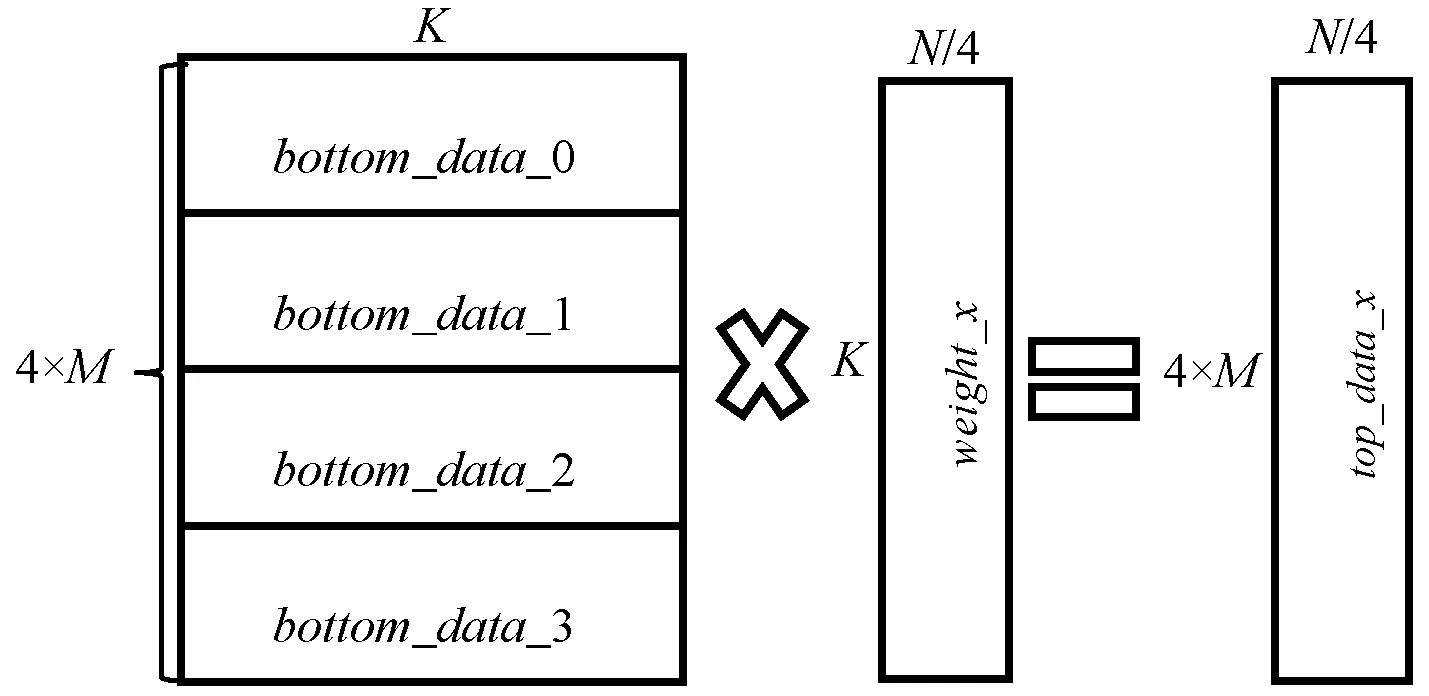
图6 top_data输出计算图

(3) 所有工作节点向其他工作节点广播自己的偏差bias_data，工作节点收到其他工作节点的bias_data后按顺序进行拼接。然后使用拼接好的bias_data和偏差权重bias_weight的乘积与(2)中得到的top_data_x相加，得到新的top_data_x，如图7所示。

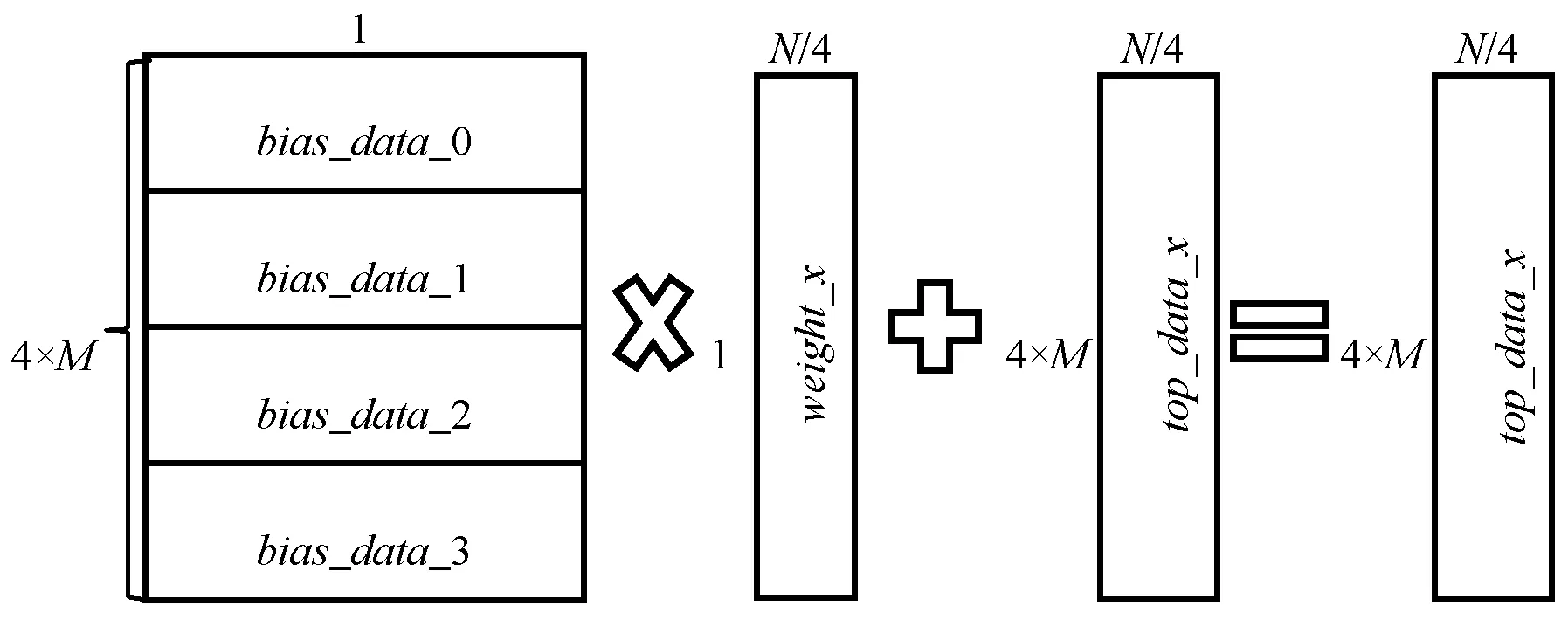
图7 top_data偏移计算图

(4) 所有工作节点向其他工作节点广播自己的top_data_x，工作节点收到其他工作节点的top_data后按顺序进行拼接，每个工作节点按新的顺序读取其最终的top_data_x，如图8所示。

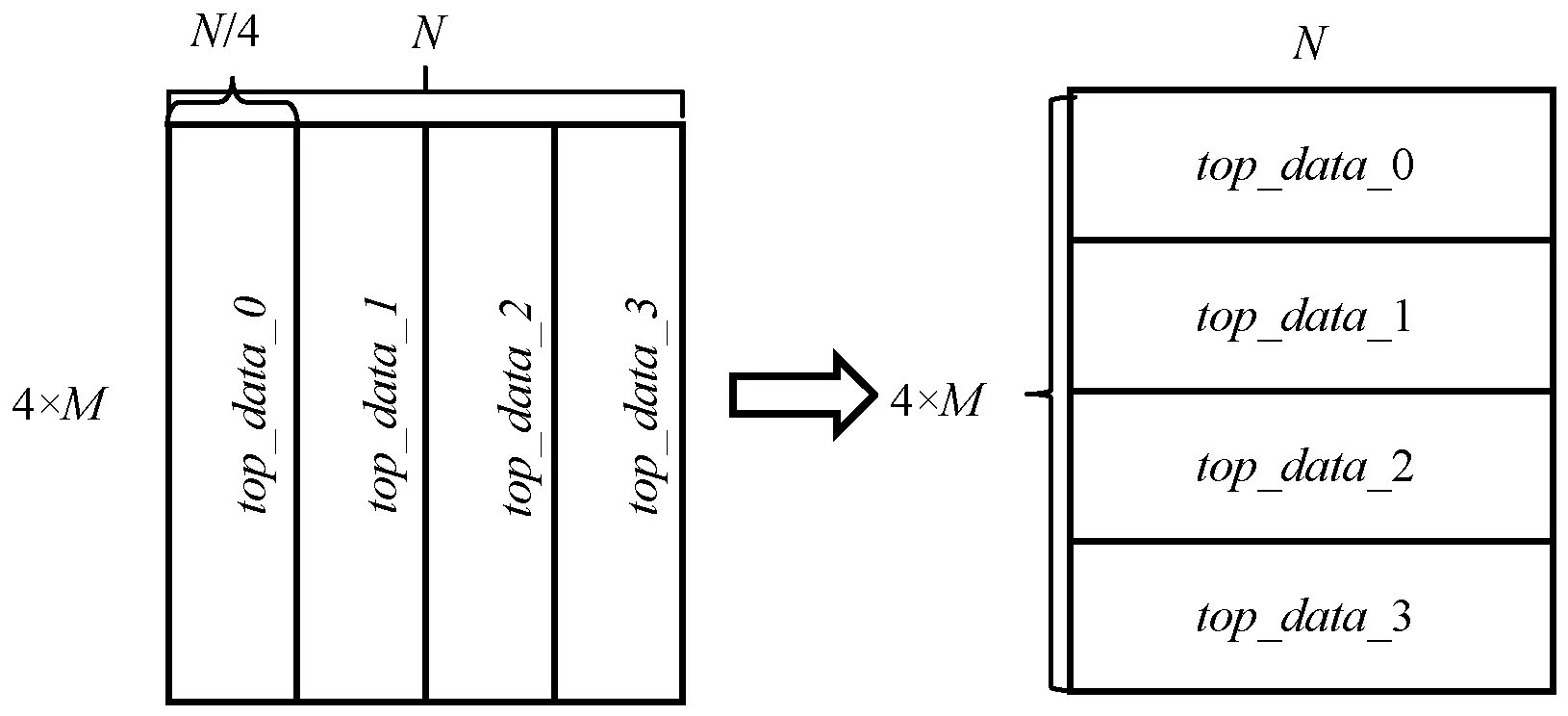
图8 top_data读取分布图

3) 反向传播过程。单节点全连接层反向传播时，特征输出梯度top_diff和特征输入bottom_data的乘积为权重梯度weight_diff;偏差bias_data和特征输出梯度top_diff的乘积为偏差梯度bias_diff;输出特征梯度top_diff和权重weight的乘积为特征输入梯度bottom_diff。模型并行时，对网络参数进行了切分，需要先进行数据的同步变换，再进行计算。同前向传播一样，以四个工作节点为例，进程号分别为0、1、2、3;相对应的数据结构为xx_0、xx_1、xx_2、xx_3。如2号进程的特征输出梯度为top_diff_2。

具体算法如下：

(1) 所有工作节点向其他工作节点广播自己的top_diff_x，工作节点收到其他工作节点的top_diff后按顺序进行拼接,并按新的顺序读取该工作节点对应的top_diff_x，如图9所示。

图9 top_diff拼接变换图

(2) 所有工作节点向其他工作节点广播自己的bottom_data_x，工作节点收到其他工作节点的bottom_data后按顺序进行拼接,如图10所示。

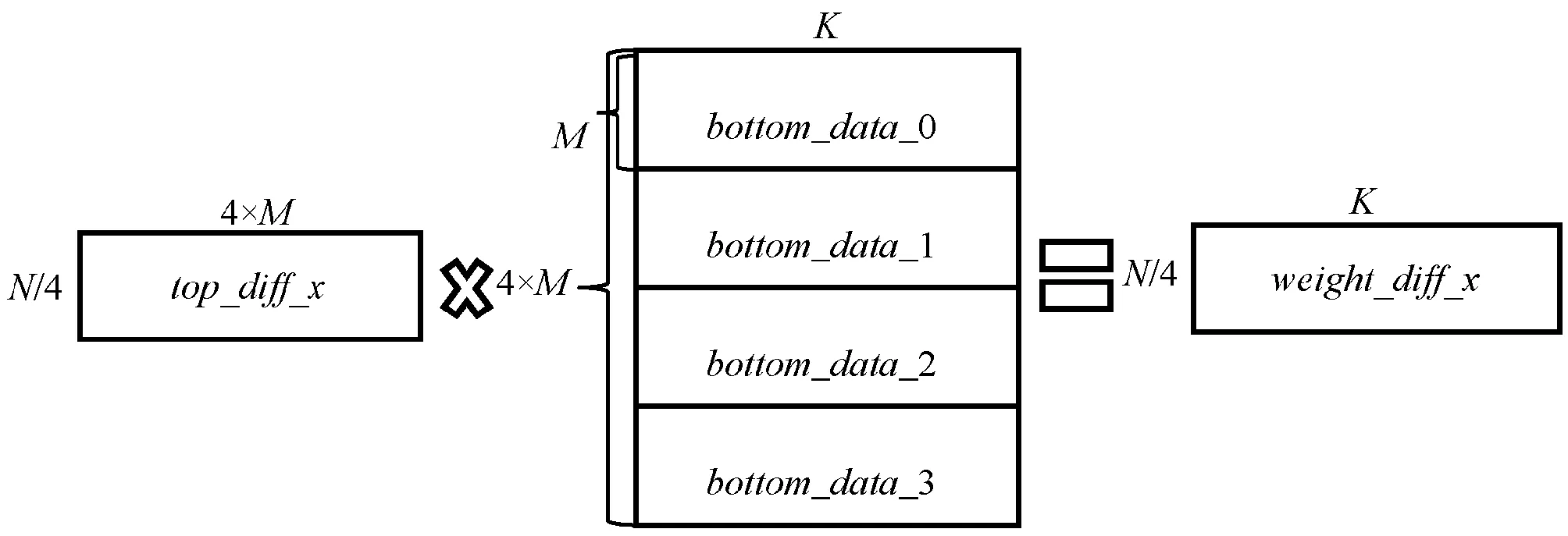
图10 权重梯度计算图

(3) 工作节点使用获得的top_diff_x和bottom_data计算权重梯度weight_diff，如图10所示。

(4) 所有工作节点使用获得的top_diff_x和weight计算bottom_diff_x,如图11所示；计算完成后所有的工作节点对bottom_diff_x进行归约操作；归约操作完成后，所有工作节点读取其对应的bottom_diff_x，如图12所示。

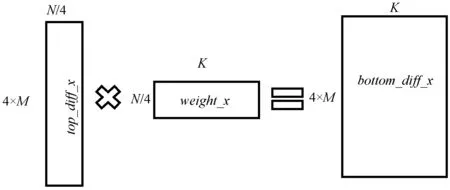
图11 bottom_diff计算图

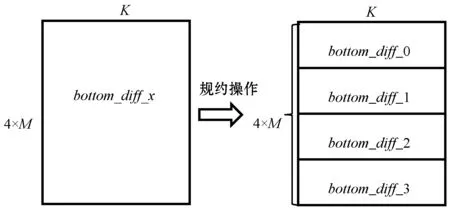
图12 bottom_diff归约图

(5) 所有工作节点向其他工作节点广播自己的bias_data_x，工作节点收到其他工作节点的bias_data后按顺序进行拼接，如图13所示。

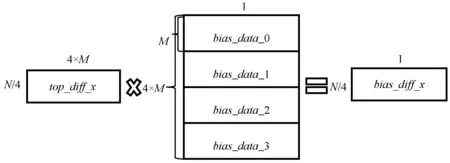
图13 bias_diff计算图

(6) 工作节点使用top_diff_x和bias_data计算bias_diff，如图13所示。

4 性能分析与优化

数据并行和模型并行都基于同步梯度更新的分布式随机梯度下降算法对网络参数进行优化，因而两者的计算量是相等的。数据并行和模型并行的性能取决于不同工作节点之间的数据同步效率，在硬件性能和网络聚集算法一定的前提下，不同工作节点之间的数据同步效率有两部分影响因素，分别是同步数据量和网络同步时延。

4.1 同步数据量

全连接层数据并行时，同步的数据为网络权重梯度和偏差梯度，数据量大小为K×N+N，K和N为网络权重矩阵的行数和列数；全连接层模型并行时，数据传输量为正向传输数据量和反向传输数据量之和，大小为3×M×K×rankcount+2M×N×rankcount，M表示Batchsize，rankcount表示工作节点数量。

当M×rankcount<(K+1)×N/(3×K+2×N)时，全连接层模型并行同步的数据量少于数据并行同步的数据量。在卷积神经网络中，K和N的值是确定的，因此，当M和rankcount变大时，模型并行同步的数据量越大，其优势相比于数据并行变小。

4.2 网络同步时延

对相同的传输数据量，网络同步时延与网络传输次数成正比。全连接层进行数据并行时，整个网络采用数据并行，可以将分散的梯度信息内存整理成连续的一段内存，从而可以在一次网络聚集平均操作中完成梯度信息的同步。全连接层进行模型并行时，需要对运算矩阵、计算结果等进行同步操作，增加了网络同步次数。具体网络聚集次数如表1所示。

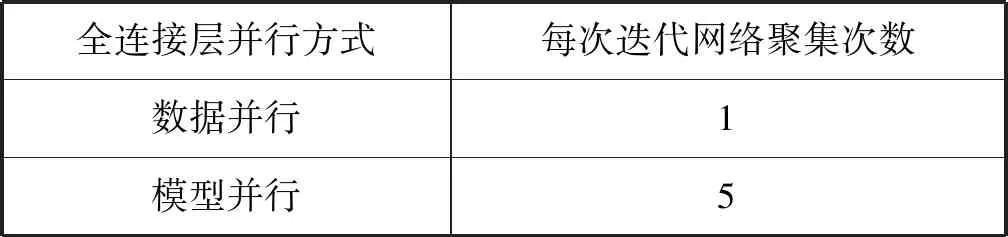
表1 全连接层数据并行和模型并行网络聚集次数对比

对全连接层不同并行方法的同步数据量和网络同步时延分析可以发现，当全连接层网络参数量较少时，采用数据并行效率更高。

在卷积神经网络中，当有多个全连接层时，不同全连接层的网络参数往往分布不均匀，如表2所示。因此，可以对参数量较少的全连接层采用数据并行。

表2 卷积神经网络全连接层参数分布表 MB

5 实 验

5.1 实验设计

选择国产超级计算机系统和深度学习框架Caffe进行实验。每个处理器作为一个工作节点。设计两个实验，分别验证CNN并行方法的正确性和性能。

5.2 正确性验证

选用Cifar10-quick网络模型和Cifar10数据集，在单节点、网络数据并行、卷积层数据并行、全连接层模型并行的情况下对网络进行训练。训练结果如表3所示。

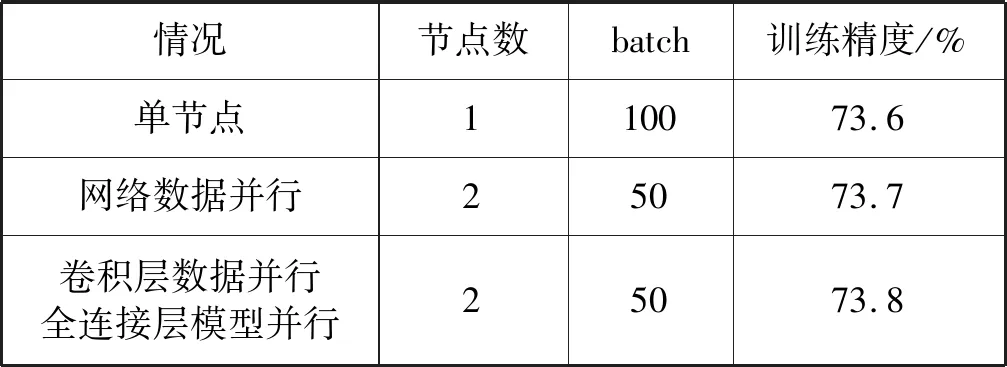
表3 数据并行和模型并行正确性验证表

可以看出，三种情况下训练网络均能有效收敛，验证了卷积层数据并行、全连接层模型并行方法的有效性。

5.3 性能测试及分析

选用VGG-16网络模型和Imagenet数据集进行性能测试。实验中，卷积层采用数据并行方式，每层全连接层分别进行数据并行和模型并行，并对性能进行对比。实验选择的并行力度为2、4、8；Batch size范围为1～128。实验结果如图14-图16所示。

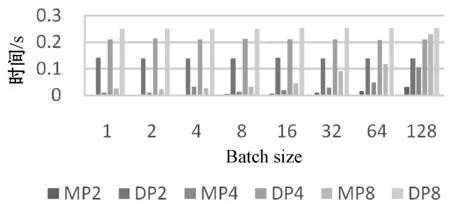
图14 FC1层数据并行和模型并行通信时间对比图

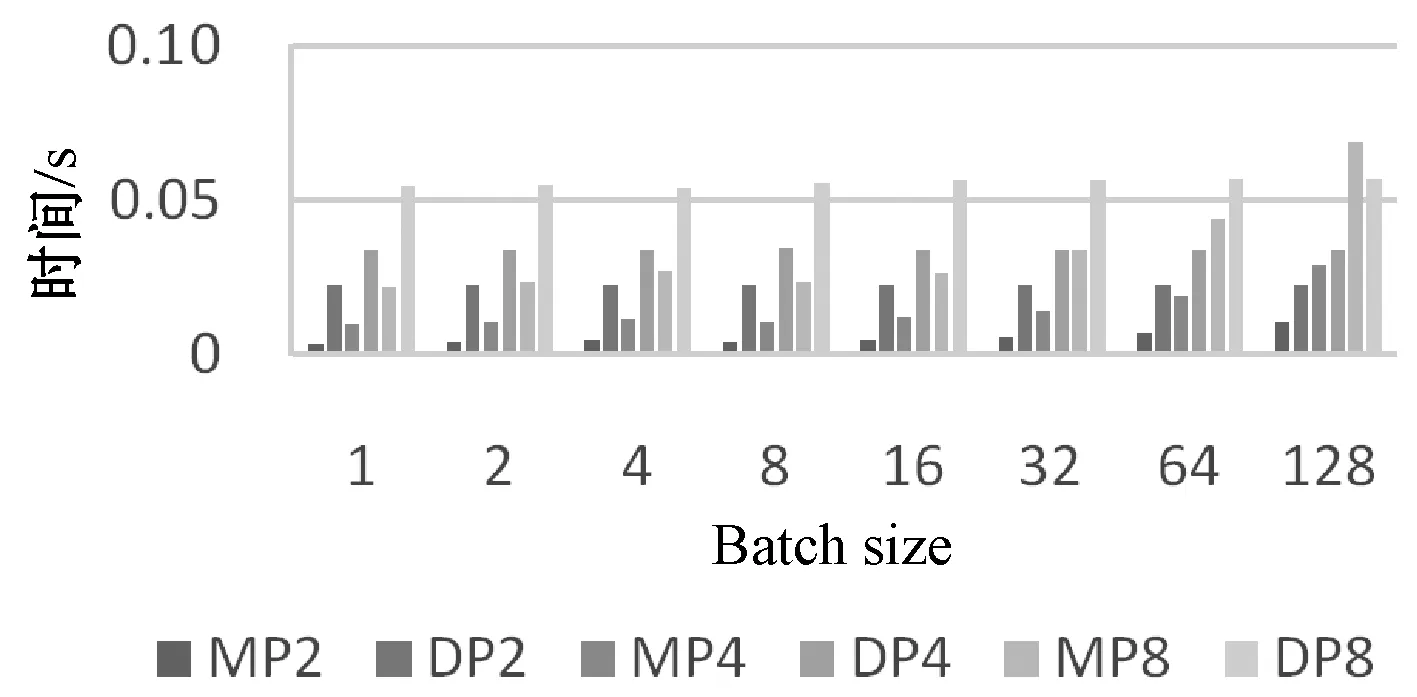
图15 FC2层数据并行和模型并行通信时间对比图

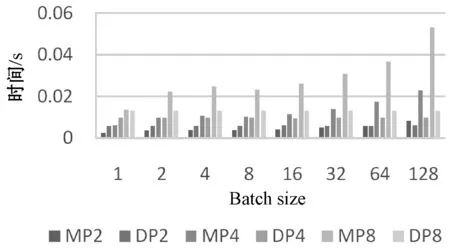
图16 FC3层数据并行和模型并行通信时间对比图

图14-图16中，MP2、MP4、MP8代表该全连接层模型并行，并行粒度分别为2、4、8；DP2、DP、DP8代表该全连接层数据并行，并行粒度分别为2、4、8。FC1、FC2、FC3表示网络中第一到第三全连接层，含有的参数量分别为102.76、 16.78、4.10 MB。

由图14可以看出，对第一个全连接层，在并行粒度为2到8，Batch size为1到128时，模型并行所用时间均少于数据并行所用时间。在并行粒度一定时，模型并行相对于数据并行的优势随着Batch size的增大而逐渐变小。在Batch size一定时，模型并行相对于数据并行的优势随着并行粒度的增大而变小。在Batch size=1，并行粒度为2时，模型并行相比数据并行对FC6层的加速可达33倍。

由图15可以看出，对第二个全连接层，在并行粒度为2到4，Batch size为1到128时，模型并行所用时间少于数据并行所用时间。并行粒度为8时，Batch size为1到64时，模型并行所用时间少于数据并行所用时间。Batch size为128时，模型并行所用时间比数据并行多，对第二全连接层采用数据并行效率更高。在Batch size=1，并行粒度为2时，模型并行相比数据并行对FC2层的数据加速可达6倍。

由图16可以看出，对第三个全连接层，在并行粒度为2，Batch size为1到64时，模型并行所用时间少于数据并行所用时间；在Batch size为1，并行粒度为2和4时，模型并行所用时间少于数据并行所用时间；其他情况下，模型并行所用时间大于数据并行所用时间，对该全连接层采用数据并行效率更高。

6 结 语

本文基于国产超级计算机系统对卷积神经网络进行并行方法研究，根据卷积神经网络参数量分布不均匀的特点，对卷积层进行数据并行，对参数量较多的全连接层进行模型并行，对参数量较少的全连接层进行数据并行。实验结果表明，对全连接层采用模型并行相比对该层采用数据并行在训练效率上最大加速可达33倍。