基于非扩展熵相似度的三维医学图像配准

李碧草 李润川 刘洲峰 李春雷 王宗敏

1(中原工学院电子信息学院 河南 郑州 450007) 2(郑州大学信息工程学院 河南 郑州 450001) 3(郑州大学互联网医疗与健康服务河南省协同创新中心 河南 郑州 450052)

0 引 言

在医学成像、计算机视觉、遥感成像领域，图像配准是一个非常重要的技术。配准算法在医学图像处理研究中，如计算机辅助诊断和肿瘤放射治疗方面有着重要的作用。医学成像过程中，由于病人体位的变化及器官和组织的移动，不同时间采集的医学图像间往往存在空间变换，医生为了更好地掌握病灶的信息，往往需要从不同模态的图像(比如MRI、CT和US等医学图像)获取病灶的互补信息，从而更精确地诊断病情。为了给医生提供不同模态图像的互补信息，需要一种鲁棒的多模态配准算法对图像进行配准融合。

目前的图像配准方法通常可以分为基于特征和基于密度两大类[1]。基于特征的配准算法包括特征提取和特征匹配，该类方法的配准精度很大程度上取决于特征点的提取。由于人体组织和器官及医学成像设备自身的特点，利用常见的特征提取方法提取特征点相对较难而且精度不高。本文研究基于密度的配准方法。在基于密度的配准方法中，基于互信息的配准算法[2-3]自问世之后就备受关注。一些学者对基于互信息的配准算法进行改进，提出归一化的互信息配准算法[4]、结合梯度信息的互信息配准算法[5]、基于互累积剩余熵相似度的配准算法[6]等。这些算法中的相似性测度都是由香农熵构造的，然而Antolin等[7]指出香农熵的扩展性使得基于香农熵的信息论相似性测度并未考虑两个独立随机变量间的相互作用。为此，学者引入一个具有非扩展性的Tsallis熵，利用其性质[8]提出一种相似性测度，以此相似度作为配准标准进行医学图像配准。受文献[7]的启发，本文利用Arimoto非扩展熵提出一种新的相似性测度，以此建立多模态医学图像配准模型，提高图像配准的精度。

1 非扩展熵相似性测度

与香农熵不同，Arimoto熵是一种非扩展熵，也是香农熵的一种推广。本文利用Arimoto熵的性质，构造一种相似性测度。

1.1 Arimoto熵

假设一个离散随机变量X，其概率分布为P=(p1,p2,…,pM)，则X的Arimoto熵定义为[9]：

(1)

依据洛必达法则求得当α→1时，Arimoto熵的极限就等于香农熵，因此Arimoto熵是一种广义熵。Boekee等[10]研究了Arimoto熵的一些重要的性质，下面仅讨论本文用到的其中几个性质：

(1) 非负性。

Aα(X)≥0α>0,α≠1

(2)

(2) 非扩展性。另给一个离散随机变量Y，当X与Y相互独立时，它们的联合Arimoto熵与边缘Arimoto熵存在如下关系：

(3)

可见，除了两个变量边缘Arimoto熵的和之外，联合Arimoto熵还包含一个乘积项，该乘积项表示两个随机变量间的相互作用。

(3) 凸性。

Aα(tX1+(1-t)X2)≥tAα(X1)+(1-t)Aα(X2)

(4)

(4) 对称性。对称性是指互换概率分布中任意两个概率分量的位置，Arimoto熵的值不会发生变化，即：

Aα(…,pi,…,pj,…)=Aα(…,pj,…,pi,…)

(5)

此性质与香农熵的对称性一样，根据Arimoto熵的定义很容易验证。

(5) 极值性。

(6)

式(6)中等号成立的条件是：当且仅当pi=1/M，i=1,2,…,M。极值性也是一个很重要的性质，根据极值性和非负性可以看到，当M和α的值给定时，Arimoto熵的值是有界的。

1.2 Jensen-Arimoto散度

受文献[11]的启发，根据詹森香农散度的定义并结合Arimoto熵的性质，提出了一个新的散度测量——詹森Arimoto散度(Jensen-Arimoto Divergence，JAD)。与詹森香农散度一样，JAD也可以用来量化随机变量之间的相似程度。

定义1假定X=(x1,x2,…,xM)是一个随机变量，其概率分布为P=(p1,p2,…,pM)，则概率分布P的JAD定义为[12]：

α>0,α≠1

(7)

式中：Aα(·)代表Arimoto熵；ωi表示加权因子，而且ωi≥0，∑ωi=1。由于当α趋向于1时Arimoto熵的极限是香农熵，因此当α→1时JAD的极限为詹森香农散度(Jensen-Shannon Divergence，JSD)。

定理1当p1,p2,…,pM为退化分布时，JAD能获得最大值Aα(ω)，这里pi=δij，δij表示克罗内克符号(Kronecker Symbol)，即当i=j时，δij=1，否则δij=0。

2 图像配准算法

在医学成像领域，模态是指不同类型的成像方式，如磁共振成像、CT成像、超声成像等。多模态医学图像配准中，待配准的对象是不同模态的图像。首先建立配准模型，然后选择合适的空间变换，再利用上文介绍的相似度作为目标函数，最后采用拟牛顿法对目标函数进行优化，获得最终的变换参数，完成多模态医学图像的精确配准。

2.1 图像配准框架

给定两幅待配准图像，一幅记为参考图像R，另一幅为浮动图像F。图像配准可以看作寻找待配准图像间的空间变换的过程。设x=(x,y,z)T为参考图像上的任意一个像素点，它经过空间变换后对应于浮动图像中的点x′=(x′,y′,z′)T，两点之间的关系表述为：

x′=Tμ(x)

(8)

式中:Tμ(·)是空间变换函数；μ为变换参数，这里的变换可以是刚体变换、仿射变换甚至是弹性形变。图1表示两幅图像对应坐标之间的空间变换关系,(a)中圆点的坐标为x，(b)中星号点的坐标为x′。

(a) (b)图1 图像坐标的空间变换关系

由此F与R的配准过程可以看成如下优化问题：

(9)

式中：S用来衡量两幅图像的相似性测度，当R(x)和F(Tμ(x))完全配准时，该相似度取得最大值，符号“∘”代表空间变换Tμ作用于浮动图像。图像配准框架的示意图如图2所示。

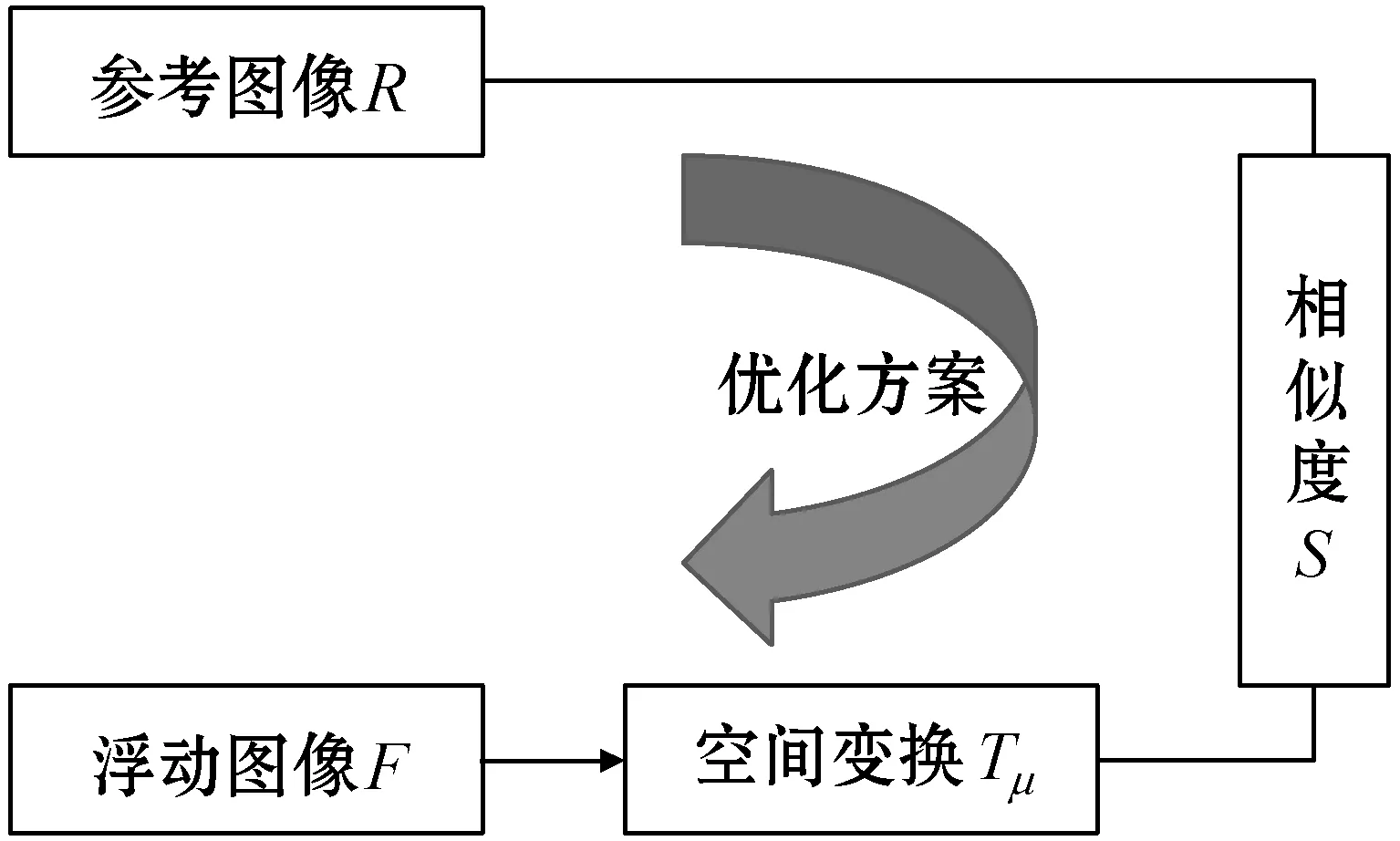
图2 图像配准框架示意图

2.2 空间变换模型

由于本文的实验对象是脑部图像，因此我们主要考虑刚体变换。刚体变换包含平移和旋转，对于三维图像来说，刚体变换有6个自由度：x、y、z方向上的平移量与绕x、y、z轴的旋转角度。三维图像的刚体变换可用矩阵形式表示为：

X′=RX+t

(10)

式中：X=(x,y,z)T和X′=(x′,y′,z′)T分别代表变换前后图像中像素点的坐标；R是3×3的旋转矩阵；t为3×1的平移向量。旋转矩阵R可以用三个矩阵的乘积来表示：

R=r(x)r(y)r(z)

(11)

矩阵r(x)、r(y)和r(z)可以用三个旋转角度表示：

(12)

(13)

(14)

式中：α、β、γ分别代表图像绕x、y、z轴的旋转角度。由此三维刚体图像配准的目的就是通过某种优化方法寻找使得待配准图像间的相似度最大时的6个变换参数。

2.3 相似性测度

本文利用第1节中构造的基于Arimoto熵的相似度来衡量两幅图像间的相似程度，将两幅图像看作随机变量，那么用它们的灰度概率分布计算其相似度。给定参考图像R和浮动图像F，及它们之间的空间变换Tμ，假设用于估计概率分布的箱子数(Number of bins)为M，让f=(f1,f2,…,fM)和r=(r1,r2,…,rM)分别为F(Tμ(x))和R(x)的灰度级。式(7)中，令JAD定义中的pi=pi(F(Tμ(x))|R(x))，i=1,2,…,M，表示已知参考图像前提下变换的浮动图像的条件概率分布，使用两幅图像的灰度级可以将条件概率分布重新写为pi=p(F=fj|R=ri)=p(fj|ri)，然后再用参考图像的概率分布作为加权因子，即ωi=p(R(x))=p(R=ri)=p(ri)，将pi和ωi代入JAD可得：

JAα(F(Tμ(x)),R(x))=

(15)

将式(15)中的JA测度替换S代入式(9)的配准框架，接下来的工作就变成如何求该配准框架最优解的问题。

2.4 优化方案

与梯度下降的优化方法相比，牛顿法中二阶信息的应用能够提供更好的理论收敛性质[13]，但是海森矩阵(Hessianmatrix)及其求逆的计算非常耗时，为此有学者提出拟牛顿法。该方法不需要计算海森矩阵的逆，而是用它的估计来代替，因此并不需要计算目标函数的二阶导数。本文采用拟牛顿法的一个变种——L-BFGS优化方法[14]，来寻找目标函数的最大值。利用泰勒级数对目标函数进行展开，只保留前三项得到：

S(μ+Δμ)≈S(μ)+ΔμT·▽S(μ)+

(16)

式中：Δμ表示参数向量的增量。对于L-BFGS方法，参数向量第k+1步迭代更新可以由第k步得到：

μ(k+1)=μ(k)-(H(k))-1·▽S(μ(k))

(17)

式中：(H(k))-1代表每次迭代的步长，是海森矩阵逆的估计，并非真实计算的海森矩阵的逆；▽表示梯度算子。接下来需要计算目标函数关于变换参数的导数：

(18)

式中：n表示空间变换模型中参数(自由度)的个数。对于三维图像的仿射变换，n=12。

要计算目标函数关于参数μ的导数，首先要推导出连续的目标函数表达式，本文将采用基于B样条的Parzen窗来估计图像的概率密度函数。设β(0)和β(3)分别代表零阶和三阶B样条函数，由于参考图像在配准过程中并不受变换参数μ的影响，因此采用零阶B样条函数来估计参考图像的概率分布。对于空间变换后的浮动图像，三阶B样条函数用于估计其概率密度函数。那么根据多维B样条函数的可分离性，R(x)和F(Tμ(x))的联合概率密度函数可由它们各自的边缘概率密度函数相乘得到：

(19)

通过计算得到相似性测度S关于变换参数μ的导数如下：

(20)

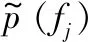
(21)

式中:β′(3)表示三阶B样条函数的导数；∂F(t)/∂t代表变换的浮动图像F(Tμ(x))的梯度；∂(Tμ(x))/∂μ为空间变换模型关于参数μ的导数。

本文的配准实验中，采用的L-BFGS优化算法的停止条件为：相邻两步迭代的目标函数值之差小于0.01或者迭代次数大于预先设定的值，本文设定该值为100。

3 实验结果与分析

为了验证本文算法的性能，我们选择不同模态的三维头部磁共振图像进行实验。这些测试图像来源于蒙特利尔神经医学部的BrainWeb数据库[15]，包含三种不同类别的磁共振图像：T1加权、T2加权和PD加权的MRI。三组数据的尺寸都为181×217×181，在物理坐标下每个体素的大小为1 mm×1 mm×1 mm。而且这三组图像的所有层都是相互对应的。图3显示了三个MRI图像的三个正交层。

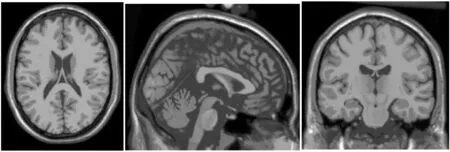
(a) T1加权MR

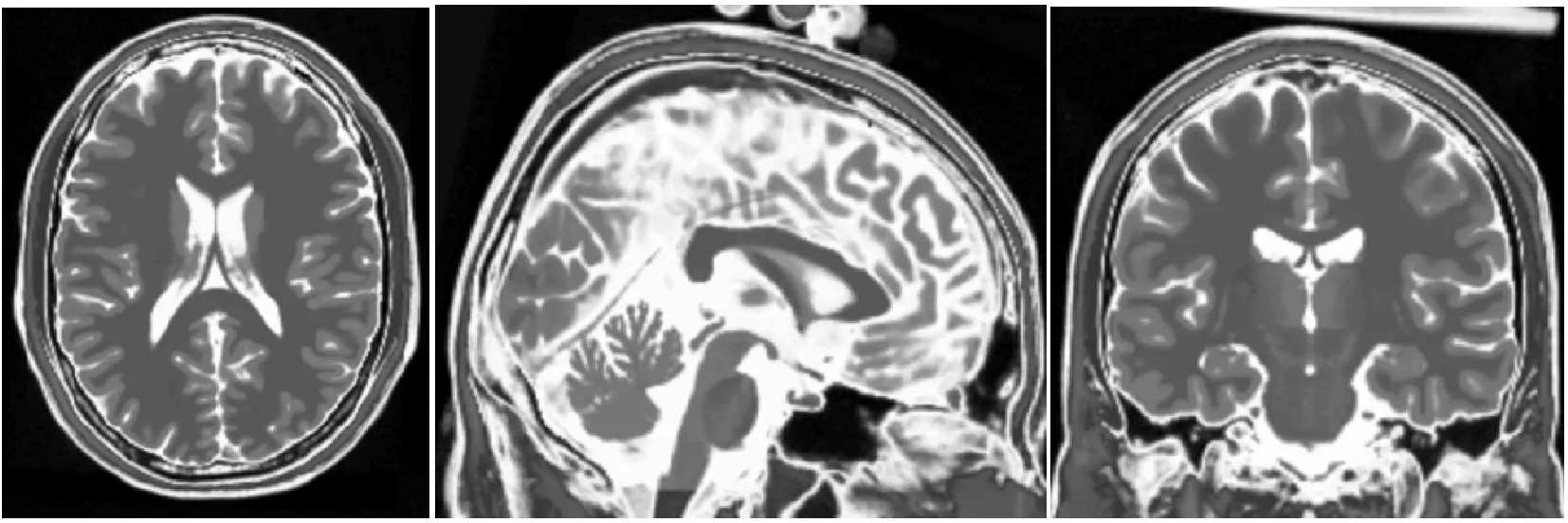
(b) T2加权MR

(c) PD加权MR，每一行分别表示轴向面、矢状面和冠状面图3 脑部磁共振图像

接下来的实验采用图3中的(a)、(b)和(c)作为实验图像来执行配准算法。使用本文算法进行图像配准时，需要考虑两个主要因素：参数α对Arimoto熵的影响和计算熵时所选取的图像块尺寸。

为了验证所提算法的性能，三种MR图像组成三对测试图像：MR T1&MR T2、MR T1&MR PD及MR PD&MR T2，将每组测试数据中的前者作为参考图像，然后利用已知的3D刚体变换(真实值)对后者执行变换，把变换后的图像作为浮动图像，如图4所示。

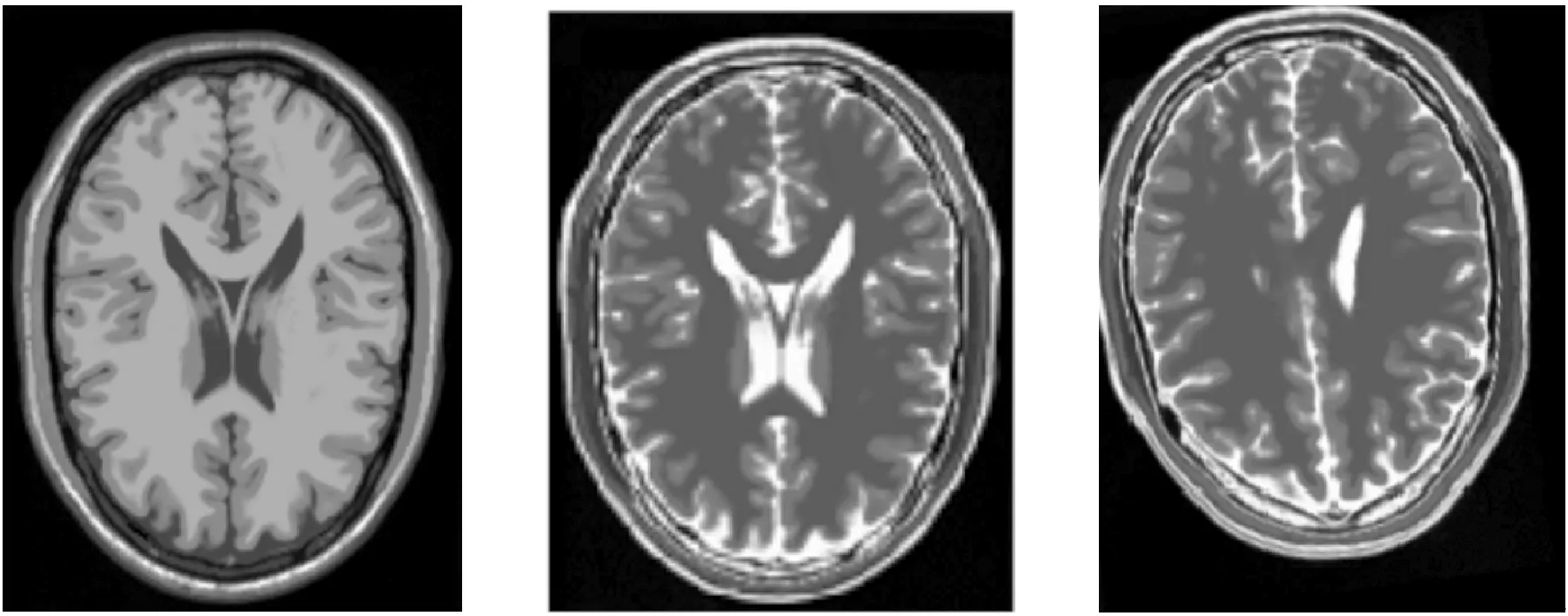
(a) MR T1图像作为参考图像 (b) MR T2图像 (c) 3D刚体变换后的MR T2图像作为浮动图像图4 测试图像

在每组测试图像中，选择30个3D刚体变换对后者图像进行变换生成30幅浮动图像，这些变换的平移及旋转参数随机产生，并服从以(10 mm,8°)为均值，(2 mm,2°)为标准差的正态分布。由于三组测试图像最初是对齐的，所以这30个刚体变换的参数即为配准的真实值。为了能定量地评估配准方法的精度，我们将利用配准方法得到的参数值与真实值的差异作为配准误差，然后比较所提算法(JAD)与另外两种方法NMI和CCRE的配准误差。

表1展示了这三种方法应用到三组实验数据的配准误差。可以看出，在处理多模态图像配准时，与另外两种方法相比本文方法获得了较低的配准误差。三组实验的配准精度都达到了亚像素级，而基于CCRE相似度的算法配准效果相对较差，特别在配准T2加权MR与PD加权MR时，误差超过了一个像素。收敛范围也是衡量一个相似度优劣的重要指标，也就是说，当待配准图像之间存在不同大小的变换时，尤其是当图像间的误匹配很大时，一个鲁棒的配准算法也能够获得最优变换。为了测试JAD相似度的收敛范围，使用三维的MR T1和MR PD作为测试图像，并执行五组实验，每一组中采用30个3D刚体变换生成30幅浮动图像。

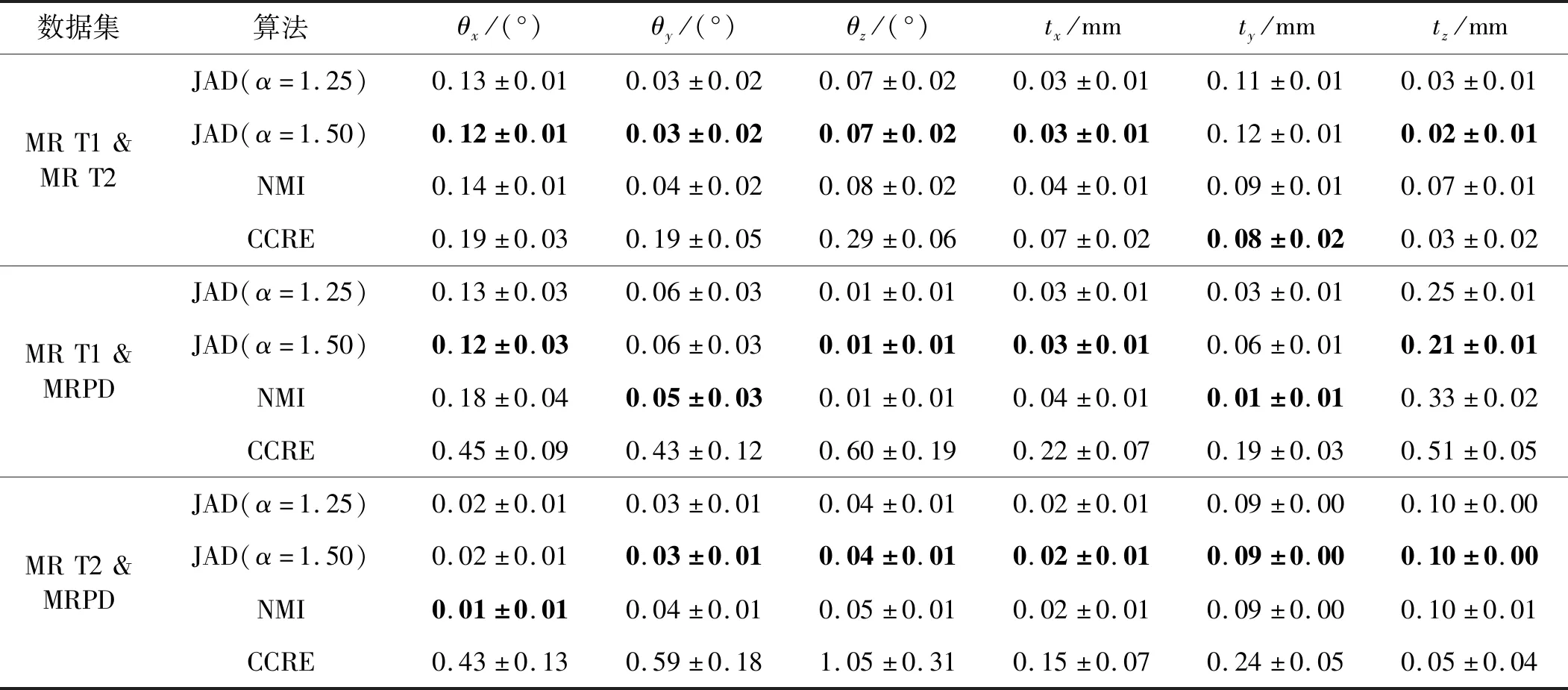
表1 执行30次3D刚体配准实验的误差均值±标准差

五组实验中采用的刚体变换参数分别来自五个不同大小的区间：[-10,10]，[-20,20]，[-30,30]，[-40,40]和[-50,50]，单位是mm或度数。为定量分析配准结果，引入成功率的概念，算法的成功率定义为在所有的实验中成功次数所占的比例，所谓的“成功”代表优化算法在100次迭代中能够收敛于最优解。图5描述了利用三种方法执行五组配准实验的成功率。可以看出，当初始变换较小时，三种方法都能获得到很高的成功率，而随着变换的增大，CCRE方法的配准成功率下降很明显，JAD和NMI相似度的成功率也有所降低，但JAD能够提供比NMI稍高的成功率。综上所述，JAD拥有较大的收敛范围，并且当图像间存在较大变换时，可以得到更多的配准次数。

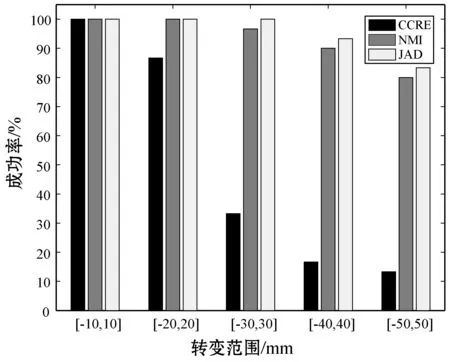
图5 不同大小变换下三种配准方法的成功率比较

4 结 语

针对传统基于互信息相似度的图像配准方法，本文提出一种基于非扩展熵相似度的多模态医学图像配准算法。首先，研究Arimoto非扩展熵的性质，利用Arimoto熵构造相似性测度，用其衡量两幅图像间的相似度；其次，结合空间变换模型建立图像配准框架；然后，利用基于B样条的帕曾窗方法估计待配准图像间的联合概率分布，得到连续的目标函数；最后，采用拟牛顿优化方法对配准模型进行求解，得到待配准图像间最优的空间变换参数，实现多模态医学图像的精确配准。三维脑部磁共振图像配准实验结果表明，与归一化互信息算法和基于互累积剩余熵的配准方法相比，本文算法能够获得更高的配准精度。未来研究将考虑三维弹性配准，并进一步提高配准精度。