一种基于神经网络和Bradley-Terry模型的围棋等级分模型

赵 睿 赵银亮

(西安交通大学计算机科学与技术学院 陕西 西安 710049)

0 引 言

竞技类体育赛事和游戏等一般都依赖于等级分系统进行评价。等级分系统提供了对参赛选手水平的估计，该估计可用于安排更为公平、均衡的赛事，也能用于对未来的赛事进行结果预测，同时提供参赛选手竞技水平的动态变化以激励参赛者及观众。

多个个体之间的比较和排序通常以两两比较的形式进行。分析成对比较数据的最主要的统计模型之一是Bradley-Terry模型[1](以下简写为B-T模型)，其将比较结果的概率建模为两个选手技能βi和βj之和的函数，如式(1)所示。同时为了避免实力悬殊的选手技能评分数量级相差过大，通常采取指数形式的实力ri和rj之和，如式(2)所示。由于B-T模型在成对比较数据模型中具有良好的统计性质，因此应用广泛[2]。

(1)

(2)

Elo[3]最早为棋类赛事开发了一个增量式评级系统，该系统自1970年以来一直被国际象棋联合会FIDE采用，并在改进后因其客观性、公平性成为选手水平评估的权威方法。基于Elo等级分系统，贝叶斯评级系统Glicko[4]首次考虑了选手评分的可信度；作为Elo算法在多人赛事中的扩展，微软研究院开发的Trueskill系统[5]能从团队对战结果中推断玩家个人技能。Elo、Glicko和Trueskill算法均属于增量式模型，该类模型存在着对局信息利用不充分的问题，比如不能很好地体现出只与固定对手比赛的那些选手的竞技水平变动情况[6]。已有的增量式算法往往通过多次时间上的前向和后向运行算法来校正评分不准确性[7-9]，但简单重复运算会损害评分的时效性。不同于增量式模型，WHR[6]引入了选手水平动态变化的先验，直接计算使比赛结果的后验概率最大化的选手等级分，但其存在计算复杂度高和耗时长的问题。针对围棋对局，棋手的对局记录通常持续数年时间，等级分模型需要处理棋手水平的时效性。除此之外，让子棋是业余围棋的常见对局模式，而现有的等级分算法无法直接处理让子棋数据。

针对以上问题，本文提出基于B-T模型的神经网络等级分系统NN-Rating及其扩展形式，用于评估围棋选手的棋力水平。由式(2)可知，B-T模型与Sigmoid函数相似，在机器学习领域中，后者常作为神经网络的激活函数。对于成对比较数据，将单层神经网络中对应于对局双方的输入固定为1和-1，则经过Sigmoid激活函数后，网络输出即为输入为1的选手预估胜率，网络参数即为各选手相对实力。这种建模方法使得B-T这样的统计模型能被应用到机器学习领域，并能使用梯度下降方法简单高效地迭代或增量求解模型参数，同时使得模型易于扩展[10]。本文通过解析KGS围棋服务器[11]上的棋谱数据获取对局记录并对其建模，利用神经网络小批量梯度下降法计算棋手等级分。对于时间跨度大的对局记录，通过修改损失函数给NN-Rating模型引入一种历史衰减优化算法以关注当下的棋力水平。同时，类似引入主场优势的B-T模型，NN-Rating模型的神经网络增加处理让子棋的节点和参数，将让子对局数据纳入等级分计算。在真实围棋比赛数据集上的实验结果和分析表明，NN-Rating模型能准确计算围棋选手的等级分，获得更高的预测准确率，所得等级分与选手胜率呈正相关关系，表现出良好的客观性和稳定性。

1 相关工作

1.1 Elo等级分

Elo等级分最早应用于国际象棋评分体系中。该方法基于B-T模型计算选手预期胜率，将胜率建模为参赛双方的实力。根据对局结果增量式调整对局双方等级分，调整幅度取决于预估胜率与实际对局结果之差。经过大量对局后，所有选手等级分将稳定到真实水平附近。Elo等级分由于其公平客观性，在当今棋类、拳击和乒乓球等对抗类体育赛事中被广泛采用，并使用更符合棋手水平分布的逻辑斯谛分布取代正态分布。双方Elo等级分为Ri和Rj，则比较结果的概率表示为:

(3)

1.2 Glicko

Glicko系统首次考虑了等级分的置信度。除了计算选手评分之外，Glicko还加入了“评分误差”(Ratings Deviation，RD)，用于衡量一个评分的不确定性(RD值越高，评分越不可信)。高RD值意味着选手并不频繁地进行对战，或者该选手仅进行了很少次数的对战，而低RD值说明选手经常进行比赛。RD值的改变同时取决于游戏结果和未进行游戏的时间长度。游戏的结果经常会减少选手的RD值，而未进行对战的时间则经常会增长选手的RD值。

1.3 Trueskill

Elo等级分主要适用于1vs1型赛事，在多人组队等复杂赛事中作用受限。Trueskill算法结合了Elo方法和概率图模型，由微软研究院开发并应用于Xbot Live匹配系统中。该算法假设选手水平符合正态分布，这个分布的方差被看作是选手水平的不确定性程度，而临时发挥符合以水平为中心的正态分布，比赛预估结果取决于双方临时发挥的差值。赛后利用消息传递算法根据实际比赛结果对各选手水平随机变量进行后验推断。吴霖等[11]将Trueskill算法应用于职业围棋选手比赛数据和仿真数据，并从客观性、准确性等方面分析了算法可行性。

1.4 WHR

WHR算法采用动态B-T模型，引入了选手水平动态变化的先验，认为下一时间步的水平符合以上一时间步的水平为中心的正态分布，利用牛顿法优化选手水平参数以最大化比赛结果的后验概率。为减少计算复杂度，WHR在每次赛后采用牛顿插值法估算新的等级分，在一定对局间隔后做全局迭代。

NN-Rating模型使用小批量梯度下降法[12]迭代运算可以充分利用对局信息，同时通过修改损失函数使越久远的对局在优化中权重越低，选手水平时效性增强。相比其他模型，NN-Rating的另一优势是可以直接处理让子棋对局数据。

2 NN-Rating等级分模型

2.1 基本模型

NN-Rating模型的基本结构如图1所示。

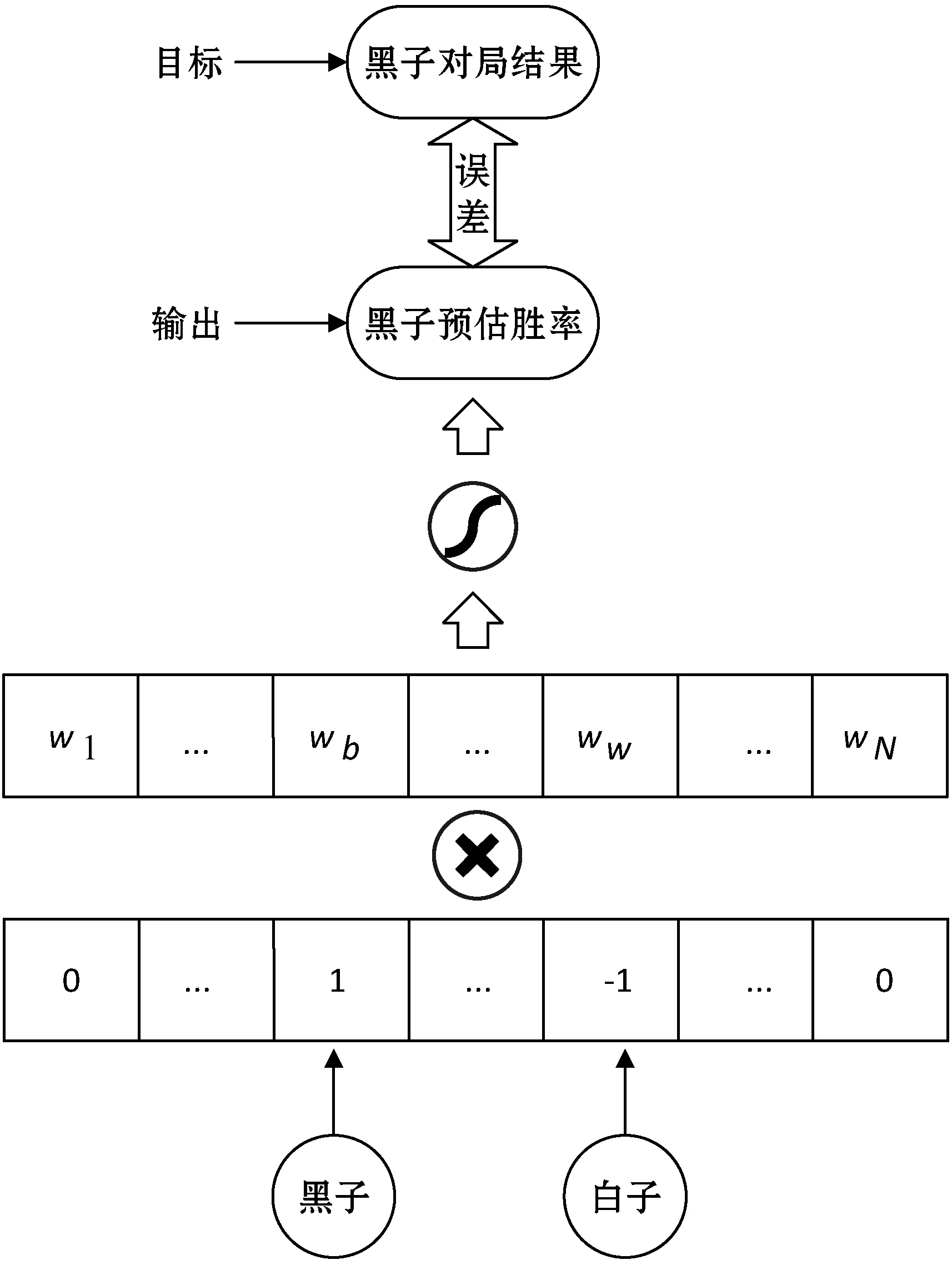
图1 NN-Rating模型基本结构

模型输入维度为N，其中N为棋手数量，棋手相对索引顺序保持固定。对于每一对局记录，通过以下方式转化为模型输入向量：参与对局的两名棋手中，黑子对应棋手输入固定为1，白子对应棋手输入固定为-1，未参与此轮对局的其他棋手输入设为0(也可设计为参与对局的两名棋手中，黑子对应棋手输入固定为-1，白子对应棋手输入固定为1，未参与此轮对局的其他棋手输入设为0。此时模型输出为白子预期胜率，模型目标应根据白子胜负或平的情况分别设为1、0或0.5。两种设计均不影响模型训练和棋手等级分的计算)。输入数据分别为w1,w2,…,wN。输入数据经过以Sigmoid函数为激活函数的单层神经网络后得到1维输出数据，由神经网络前向传播规则，输出o为：

(4)

式中:wb为本轮对局中执黑方对应参数;ww为执白方对应参数。该形式与Bradley-Terry模型相同，模型参数即为棋手对应等级分，模型输出即为黑子预期胜率。

使用NN-Rating模型的优势是可以利用梯度下降法等优化方法计算模型参数，并可以方便地扩展模型以处理让子等因素。对于每一对局记录，模型的目标ti通过对局结果按照以下方式计算：执黑方获胜则目标为1，执白方获胜目标为0，平局为0.5。模型的输出为oi。利用神经网络小批量梯度下降法优化模型参数，最小化模型输出与目标之间的均方误差损失函数，训练完成后获取模型参数即得各棋手相应的等级分。模型损失函数如下：

(5)

式中：n为对局总数。

增量式模型中选手若只与固定对手对局且二者实力相当，在对手与其他选手对局后水平变动的情况下，该选手评分却保持不变。增量式模型可通过时间上前后向多次迭代运算来解决上述问题，但这种方式对所有时间段的对局同等看待，牺牲了等级分的时效性。NN-Rating模型训练过程中随机选取部分记录进行迭代计算，因此不存在增量式模型中对对局信息利用不充分的问题。同时NN-Rating模型可通过简单修改损失函数的方法降低过去对局的权重，保证了等级分的时效性。

2.2 历史衰减模型

围棋棋手的对局记录通常持续数年时间，在时间跨度大的情况下，棋手的水平会发生一定变化。已有的历史衰退模型对之前已经发生的比赛结果做一次衰退处理，降低过去比赛的权重。

本文为了使计算出的棋手等级分更符合棋手当下的水平，使得时效性增强，对2.1节中的基本模型进行扩展。对过去的对局添加指数年度衰减系数，使距离当前越久远的对局在计算中所占权重越小。具体衰退通过修改损失函数完成，修改后原始损失函数为：

(6)

式中：d为对局发生年份与数据集中对局发生的最后年份之间的年份差。距离对局发生的最后年份越久的对局衰减得越多，最后年份当年的对局不衰减。历史衰减等级分模型的输入输出及计算方式与基本模型相同。

2.3 让子棋模型

让子棋是某些棋类活动中的特殊情况。当对弈双方棋力差距较大时，按照不让子方式进行对弈，棋力高的一方将大概率胜出；而采用让子的方式，可以削弱双方棋力差距从而可以进行基本平衡的对局。类似球类赛事中的主场优势，包含让子因素的B-T模型中黑方胜率如下：

(7)

式中：λ为要学习的让子参数;h为让子数。

已有的等级分算法中没有可以直接处理让子棋的。通过在2.1节中的基本模型中添加一个专门处理让子因素的节点和该节点对应的参数，本文模型可以直接处理不同让子数的让子棋而不需要将让子数转化为相应的Elo分值。扩展的可处理让子棋的NN-Rating模型输入维度为N+1，其中N为棋手数量，前N维输入与基本模型中相同，最后1维输入为让子数。输入数据参数分别为w1,w2,…,wN,wλ，其中前N维参数分别代表各棋手等级分，最后1维参数代表让子参数λ。在计算棋手等级分参数的训练过程中，让子参数也通过梯度下降法求解。

2.4 置信度

棋手参与对局数越多，对其等级分的计算就越接近其真实水平，所以本文引入一种启发式方法计算等级分的置信度，同时不影响梯度下降法计算棋手等级分。gi为选手i参与的对局数，则选手i等级分的置信度表示为：

(8)

式中：certaintyi为棋手i等级分的置信度;G为一个常数，表示对棋手i等级分完全置信时他需要参与的对局数，文中取值为10。置信度可作为棋手等级分的辅助指标。置信度越高，计算出的棋手等级分越接近其真实棋力。

3 实 验

3.1 数据集

KGS围棋服务器[13]是世界上最大的围棋服务器之一，包含从2001年至2018年的对局记录。通过u-go.net网站[14]可获取来自该服务器且经过初步筛选和分类的对局的SGF棋谱文件。本文采用顶级业余棋手的对局记录数据集，对弈双方中一方为业余7d及以上或双方均为业余6d。WHR算法选取了2000-11-07至2005-05-20的对局记录作为训练集，2005-05-21至2007-10-01的对局记录作为测试集，为保证与对比算法中数据集维度保持同等条件，同时避免对局记录受围棋AI的影响，本文选择2010年—2014年的高水平业余棋手对局数据作为训练集，2015年—2016年的对局数据作为测试集。通过解析SGF文件并去除无效对局(没有对局结果)，最终非让子棋训练集包括52 255条对局记录，3 591名棋手，测试集包括11 819条对局记录，其中测试集中的4 269条记录对弈双方均已在训练集出现，可用于预测准确率评估。让子棋训练集包括22 498条对局记录，4 725名棋手，测试集包括8 415条对局记录，其中测试集中的1 689条记录对弈双方均已在训练集出现，可用于预测准确率评估。

3.2 实验结果及分析

3.2.1收敛性

通过训练集上的迭代计算验证算法的收敛性。每轮迭代中采取小批量随机梯度下降法最小化模型的损失函数。学习率取值为0.01，批大小取值为512，指数衰减系数γ取值为0.95，非让子棋数据集迭代过程中模型的均方误差变化如图2所示。

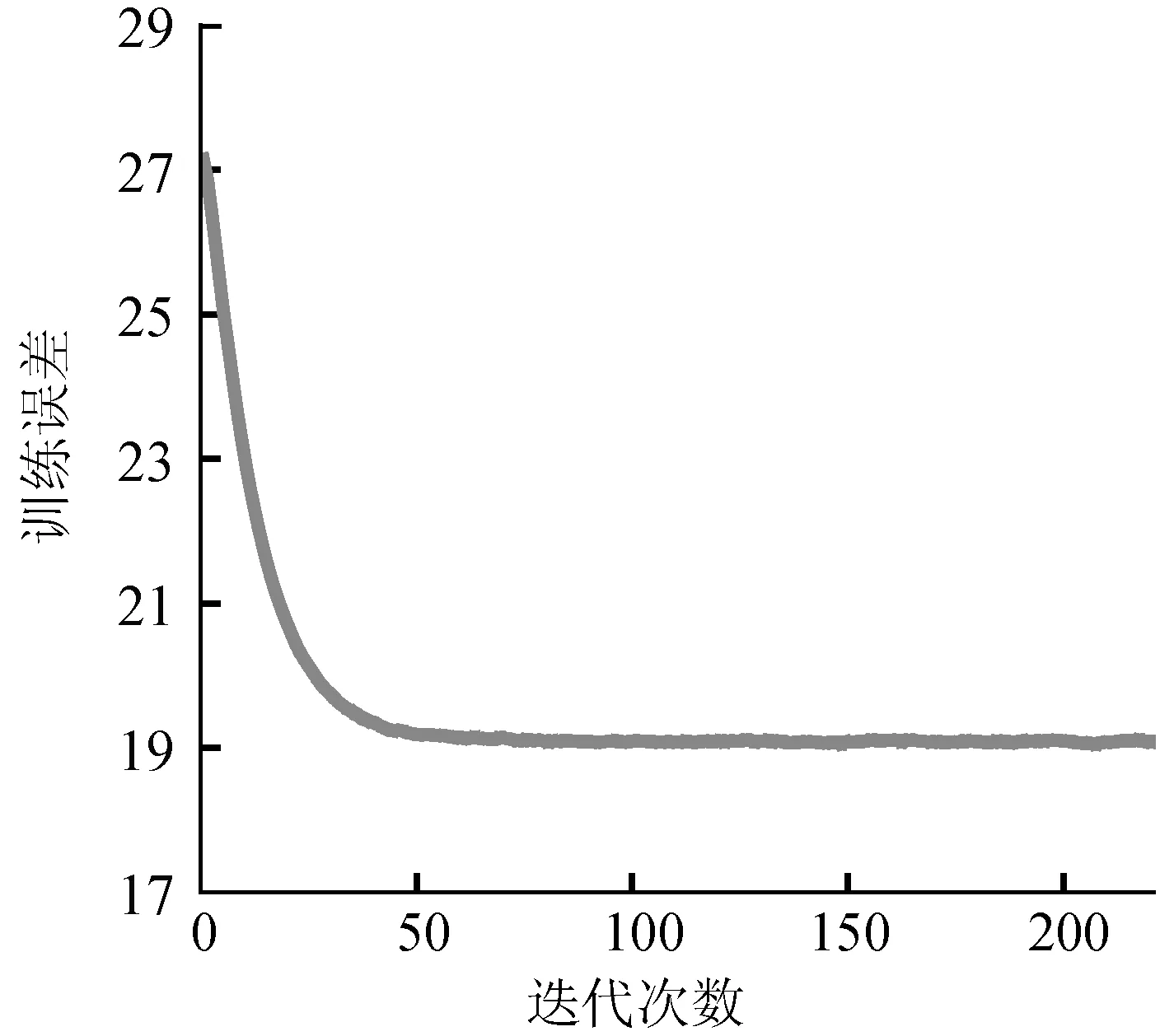
图2 训练误差的收敛性

可以看出，经过50轮迭代后，模型误差趋于稳定。最终计算出的排名前20的棋手等级分及置信度如表1所示。

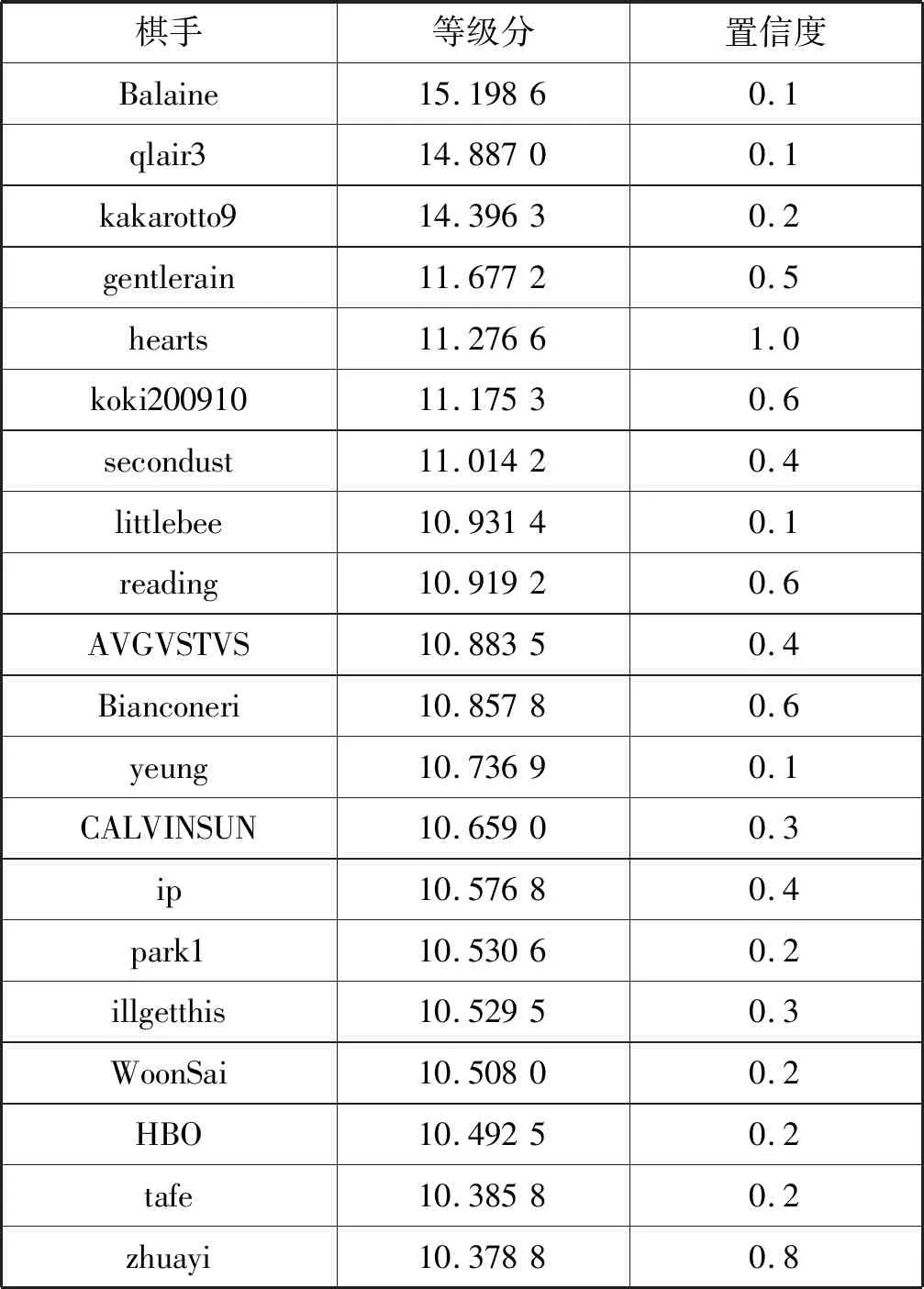
表1 排名前20的棋手的等级分和置信度

3.2.2客观性

胜率是选手实力的客观体现和衡量标准之一，利用棋手胜率与NN-Rating模型计算出的等级分之间的关系如图3所示。

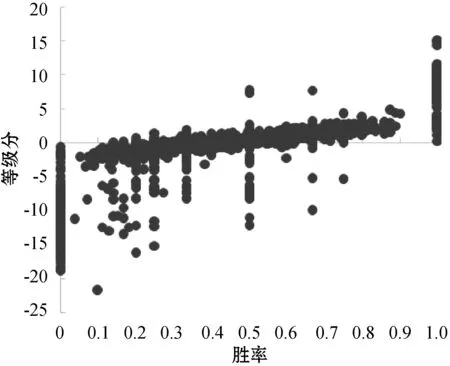
图3 胜率和等级分的关系

可以看出，胜率与等级分呈正相关关系，胜率高的棋手对应的等级分也越高，表明模型具有良好的客观性。

3.2.3准确性

(1) 分先对局记录。等级分算法的对比实验通过衡量各算法在测试集上的预测准确率完成，其中算法在测试集对局记录上预测出的胜者与对局实际结果一致则视为预测正确。各算法预测准确率如表2所示。

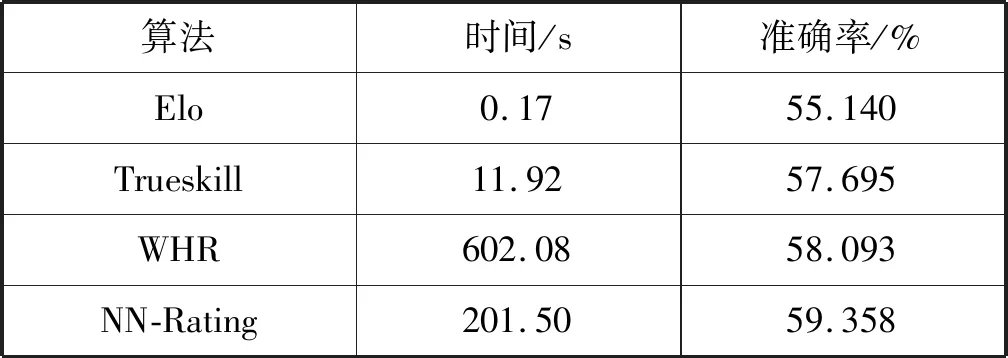
表2 不同算法在非让子棋数据集上的预测准确率

Elo算法初始等级分设为1 300分，参数k取值为16。Trueskill采取微软研究院开源算法的默认设置，初始等级分为25。吴霖等[11]未修改原始Trueskill算法，而是使用随机输入多次迭代运算来平滑结果，但损失了等级分计算的时效性，且在小数据集上的效果只略优于Elo算法，在此分析的基础上，本文选择与原始算法作对比。利用NN-Rating模型计算出的棋手等级分在测试集上预测准确率更高，表明该算法计算出的等级分更符合棋手的真实棋力。

(2) 让子对局记录。Trueskill、WHR等算法无法直接处理让子棋，因此使用NN-Rating方法在让子棋数据上进行测试，其准确率达到60.628%。

4 结 语

本文构建NN-Rating神经网络等级分模型，为等级分算法在大规模数据上的应用提供参考。本文的贡献如下：1) 基于统计学的Bradley-Terry成对数据比较模型和人工神经网络设计NN-Rating等级分模型，利用小批量梯度下降方法迭代求解模型参数，消除增量式模型中对局信息利用不充分对等级分计算准确性的影响；2) 通过修改损失函数扩展NN-Rating模型为历史衰减模型，使得距今越久远的对局记录在模型训练过程中权重越小，因而计算出的等级分时效性更强，更符合选手当下的水平；3) 针对围棋让子棋特点，借鉴主场优势特性扩展NN-Rating基本模型为让子棋模型，通过引入让子数节点和对应的让子参数，让子棋模型可以直接处理围棋对局中的让子棋，而已有的等级分算法中没有可以直接处理让子棋的。在真实赛事数据集上的实验表明模型具有良好的客观性和准确性。下一步工作除了考虑对局结果外，还将利用围棋AI分析棋手对局过程中的表现，对对局结果和棋手中间胜率建模，有助于提升等级分模型的准确性。