基于二阶库诺特博弈的电力物联网技术环境选择研究
2020-11-12刘斯扬李贵良
唐 标 杨 莉 刘斯扬 李 博 李贵良 王 恩
1(云南电网有限责任公司电力科学研究院 云南 昆明 650217) 2(云南电网有限责任公司德宏供电局 云南 芒市 678400)
0 引 言
近年来,物联网在电力系统得到广泛的应用[1],电力物联网融合5G、大数据、人工智能、边缘计算、区块链等新技术[2],以电网为枢纽,将用户、电网企业和电网设备等连接起来[3],形成数据共享共用的电力生态系统[4]。国家电网在2019年两会报告中提出加快建设“泛在电力物联网”的目标,并将电力物联网定位为能源互联网的重要组成部分[5]。为加快电力物联网建设,政府出台了一系列鼓励物联网企业研发电力物联网设备的补贴降税政策。与传统行业相比,物联网行业具有技术迭代快,寡头竞争和垄断态势共存的市场特点[6]。对物联网企业来说,利用国家优惠政策合理选择技术环境,实现自身利益最大化,是其主要目标,而不完全信息下的库诺特模型考虑信息的不对称性,认为至少有一方参与者不了解其他某些参与者的收益函数,这与物联网行业的实际情况比较吻合。
需求函数是库诺特模型分析的基础,目前大多数文献都是基于线性需求函数对相关的库诺特模型进行分析,这是因为高折扣会使得销量增加,做到薄利多销,而低折扣使得销量减少,做到少销多利,许多学者由此认为需求函数是一个单调递减的函数。周贵川等[7]通过考虑线性需求建立了一个两阶段双寡头博弈模型,分析了资源型企业间合作技术创新的模式选择、动机决定和绩效影响机制。钟美瑞等[8]通过建立线性需求函数,结合代际公平与社会偏好对金属矿产定价进行了分析。牛志勇等[9]通过建立线性需求研究了多渠道零售商线上线下同价如何抉择的问题。Chokler等[10]通过建立线性需求函数,认为信息优劣取决于公司信息化建设,表示信息并不会总是带来高利润。Roux等[11]通过建立线性需求,研究了如何用针对性惩罚来解释公司间的共谋问题。
事实上,在技术迭代速度飞快的物联网设备市场,销售商通常会针对市场需求对价格进行上下调动以增加自身利润,通过线性需求函数制定出的最优价格通常不是实际的最优价格。目前,少数学者开始在研究中使用非线性的需求函数,如:Fanti等[12]考虑非线性需求函数,研究了局部和全局动态事件;Bertran等[13]引入了二次需求函数,但依然是将其看作单调递减的函数,并未考虑供求关系影响使得价格浮动。库诺特模型中的非线性需求函数通常来源于基本 CES效用函数,Agliari等[14]通过使用 CES效用函数变形的需求函数研究了库诺特寡头模型中,有限理性的企业如何采用梯度调节机制来更新各时期的产量。
本文针对一般做法中把需求函数看作价格递减函数的局限性,结合物联网市场供求矛盾突出的现状,给出企业的应对方法:在供大于求时,企业增加折扣促进消费;在供小于求时,企业上调价格降低需求或者采取保价措施。并提出了价格上浮时的充分条件和价格保持的必要条件,这一需求函数的构建更加符合现实。另外,物联网企业之间的生产技术水平参差不齐,信息收集能力也各有不同,本文考虑市场中存在两个物联网寡头企业,在掌握不同环境技术的情境下,计算得到其产量和利润,并对利润函数进行仿真分析,找出企业利润的决定因素。在此基础上,对物联网企业生产技术水平的选择提出管理建议。
1 电力物联网企业浮动定价模型
物联网企业利用技术优势,对传统的电网系统进行改造优化,涉足电力资产管理、电力设备检修、用电信息采集分析以及电力信息通信等业务环节。在电力资产管理方面,物联网设备通过RFID技术,可以对电力设备进行自动识别和记录管理,与电网企业的管理系统同步信息。在电力检修方面,物联网设备能够进行智能化巡检,实时掌控电力设备的运行状态,及时发现、快速诊断和消除故障隐患,快速隔离故障,实现自我恢复。在用电信息采集方面,物联网设备可以实现远程抄表和用户侧电力数据分析等功能,开展电力市场分析预测。在电力信息通信方面,物联网设备可以传输语音、数据、故障录播及视频等,在配电网通信、应急通信以及智能电网等方面,为电网智能化提供必要的技术支持和保障。本文主要研究两家生产物联网电力检修设备的寡头企业之间的竞争。
1.1 二次需求函数的引入
本节引入二次需求函数,描述电力物联网设备市场的需求特性,其作用机制如图1所示。
设物联网设备的技术成本为M,市场供求情况正常时,商品价格(标准价格)为p,市场需求函数为θ(·),非技术成本为C,企业净利润为W,则:
W=(p-M)θ(p)-C
(1)
考虑实际正常市场中存在的价格浮动,记市场价格浮动率为β,相应市场需求量为θβ,非技术性成本为Cβ,企业净利润为Wβ,则有:
Wβ=(βp-M)θβ-Cβ
(2)
1.2 价格保持必要条件和价格上调充分条件
在现实中,物联网设备市场的供求情况是时刻变化的,在供大于求时,物联网企业会下调β以刺激市场需求,采取薄利多销策略;而在供小于求时,则会上调β以提高购买门槛,做到少销多利,也可采取其他措施来保价供应。通常要求满足:θβ>θ(p)与Wβ>W。因此:(βp-M)θβ-Cβ≥(p-M)θ(p)-C,这时上调幅度应满足:
(3)
当供求矛盾较大时,毫无疑问需要付出更多的非技术成本(比如增加更多人力成本、销售水平等),即非技术成本满足Cβ≥C,此时可以得到价格保持的必要条件和价格上调的充分条件:
对任意β,Cβ-C≤(p-M)(θβ-θ)+(β-1)pθβ,保持价格不变时,β=1,此时,Cβ-C≤(p-M)(θβ-θ);当Cβ-C≥(p-M)(θβ-θ)时,必然有β>1,即价格必须上调。
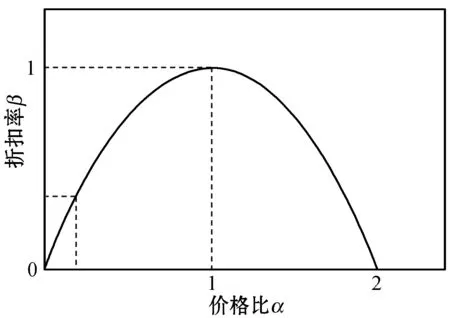
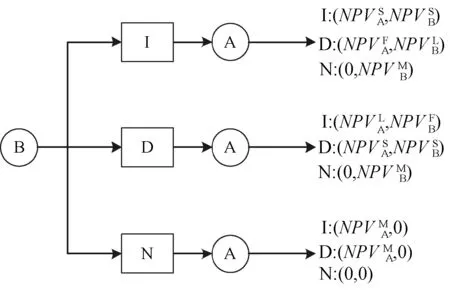
折扣定价引起的销售收益损失WL可将上述结论解释为:Cβ-C 折扣定价通常考虑价格下调问题,此时β称为折扣率。考虑到薄利多销情形下,市场中非技术成本变化不是很大,为方便运算,假定Cβ=C,则根据式(3),折扣率β需满足: (4) 为方便分析,令β取最小值,即取最大折扣,其计算公式如下: (5) (6) 由此造成的收益损失为: (7) 物联网设备在销售过程中,一个很重要的问题就是如何选取标准价p和折扣率β,以尽可能地减少销售收益损失,所以下面将研究式(7)中WL随p变化的具体情况。 (8) β=2α-α2=1-(1-α)2 (9) 图2 折扣率与价格比的关系 在特定时间内,需求量θ(p)极值点p1常发生变化,故α也随之发生变化。因为α<1,所以式(9)适用于p>M的情况,表示如抛物线左半支。 (10) 可以看出,若θ″(p1)>0,此时WL(p1) 是极小值,但θ(p1)此时也取极小值,故p1不是企业所需要的,必须给消费者式(9)的最大折扣率。 因此,对于物联网企业而言,考虑到θ″(p1)表示需求函数θ(p)在p1附近的凸性大小,得到的折扣定价策略:最大折扣率公式只与价格比α有关,与销量无关;若p1使需求量达到最大,且需求函数在该点附近凸性较小,则企业可采取β和p1作为最大折扣率和标准价。 以上结论对于物联网企业的指导意义在于,企业可根据历史销售记录对需求曲线进行拟合,从而得出θ(p),通过调整折扣率β和标准价p1来提高销售收益。以往的研究通常只考虑到需求函数是一个单调减函数,而经过上述分析可以看出其不再是单调减函数。 考虑到物联网企业销售产品时的三个价格:最低价pmin(接近技术成本的价格)、标准价p1(销量达到最大的价格)和最高价pmax(政府指导价格)。一个二次需求函数可以通过以上三个价格得出。通常,M θ′(p)=k(p1-p) (11) 式中:k>0是待定系数,给定需求函数在pmin和pmax处的取值θm、θM之后,对式(11)进行积分后方可得到需求函数: (12) 本节研究两家生产物联网电力检修设备的寡头企业之间的竞争,考虑两个市场参与者同时采取行动的情况,博弈过程描述如下。 两家物联网寡头公司A和B进行两阶段的博弈,其生产相同质量的产品,并且只进行数量竞争。第一阶段,两企业同时选择所采用的技术环境。当两企业同时决定欲采用的生产技术后,第一阶段结束,进入第二阶段。因为两企业在第一阶段同时决策采用的技术环境,所以第二阶段的数量竞争是Cournot-Nash竞争。假设第一阶段的决策会在数量竞争阶段产生n期的现金流。上述情形的博弈时序如图3所示。 图3 参与者同时移动时事件发生的时间线 假设物联网企业A在信息方面有优势,企业间的信息不对称描述如下:企业A同时熟知企业A和企业B的生产技术水平。企业B只知道自己的生产技术水平(εB)。企业B对企业A的生产技术水平方面所掌握的不完全信息可以用概率分布表示如下: (13) 企业A的环境技术水平只有企业A自己知道。两企业的信息集合分别为ISA={εA,εB,θm,θM},ISB={ε,εB,θm,θM},其中θm、θM分别表示需求函数在pmin和pmax处的取值。因为企业A在信息方面具有优势,所以在博弈树中我们将企业A的节点置于企业B之后,表示企业A对企业B有完全信息。博弈过程如图4所示。 图4 参与者同时移动时的博弈树 假设市场需求曲线接近于二次函数,具体形式如式(12)所示,得反需求函数如下: (14) 考虑两家物联网企业同时决定产量,此时,这是一个不完全信息的库诺特寡头竞争模型。因为物联网企业A知道双方的环境技术,故企业A在完全信息下最大化自身利润;物联网企业B只知道自己的技术环境,对A的技术环境不确定,企业B对于企业A技术环境的猜测是一种概率分布,因而企业B需要在不完全信息下最大化自身利润。 (15) (16) (17) 数值实验的运行环境为Intel(R) Core(TM) i5-5200U CPU @ 2.20 GHz,内存为8 GB,采用MATLAB 2016a软件进行仿真。调整企业 A与B的技术水平εA和εB,调整参数设置以更直观地观察两企业利润的决定因素,分别如图5、图6所示。 图5 企业A的利润受环境技术影响趋势 图6 企业B的利润受环境技术影响趋势 可以看出,两企业的最优反应取决于企业本身的技术环境以及对手的技术环境。企业i本身的技术环境越好(εi越大),或对手的技术环境越差(εj越小,j≠i),则企业i的产量与利润越大,所以企业在制定生产决策时,要同时兼顾考虑自身的技术环境与对手的技术环境。两家物联网企业在数量竞争阶段会产生n期的现金流。若已知折现率δ,通过将未来利润折现加总之后减去研发费用,可计算出企业i在库诺特竞争下的净利润现值NPVi。 相比物联网企业A而言,企业B的利润趋势存在一个转折点,企业B的利润随着两寡头企业之间的技术差异化降低,利润增长缓慢,而当两家物联网企业的技术差异足够明显时,利润上升趋势显著。此时足够的技术差异使得高技术企业有着自己的生存空间,在技术推动之下,逐渐开拓自己的市场,使得利润提升足够显著。 技术是推动是物联网企业成功的关键要素,各个物联网寡头企业只有通过技术差异化才能在竞争中占据主动地位。高技术的物联网企业可以通过技术差异化构筑竞争优势,在市场中寻找着自己的机会和目标市场,技术差异化愈明显,目标市场愈加庞大,企业所得收益增加也就愈显著。 未来研究思路如下:可以考虑两厂商做决定的先后顺序,用斯坦克伯格模型进行研究,在两企业两阶段不同的决策之下比较得到相对较好的决策;可以考虑企业成员的有限理性,由于企业决策层在制定策略时,最优的策略总是以更大的概率被选择,故QRE模型可以很好地刻画这种行为规则;企业决策层在制定对策时,个人的推理能力和推理方式不同,会导致每个决策者的认知层级不同,可以考虑将认知层级量化,继而加深对企业决策层有限理性的研究。1.3 折扣定价策略

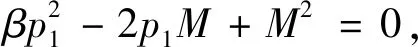
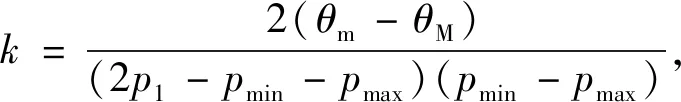
2 模型构建
2.1 参与者同时行动情形及第一阶段的技术决策

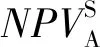
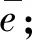
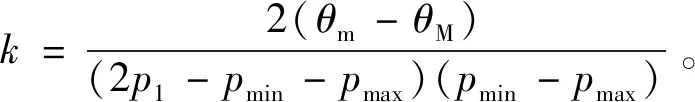
2.2 第二阶段的产量决策
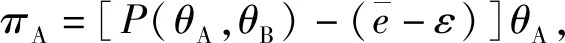
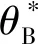
3 仿真与分析

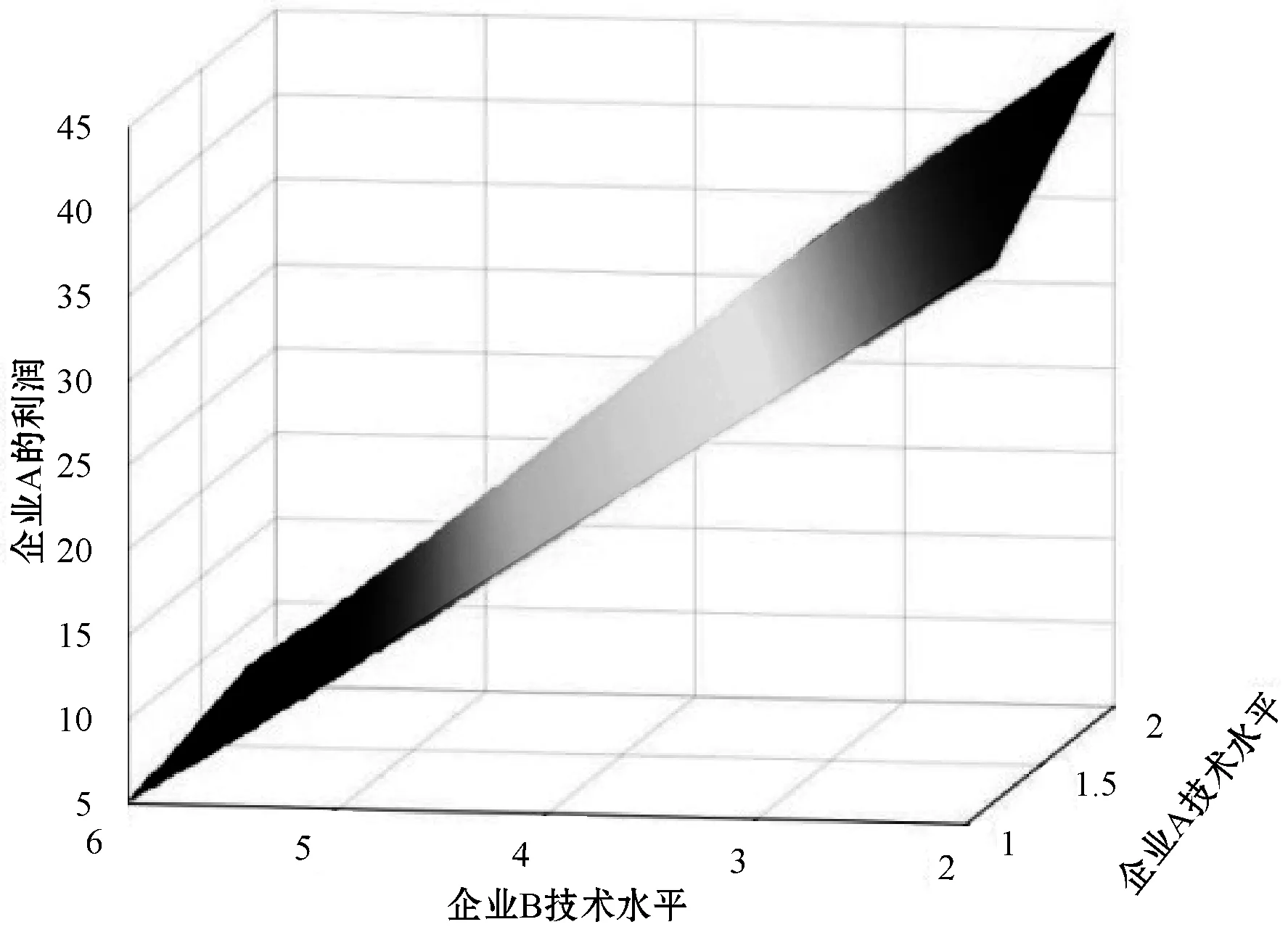
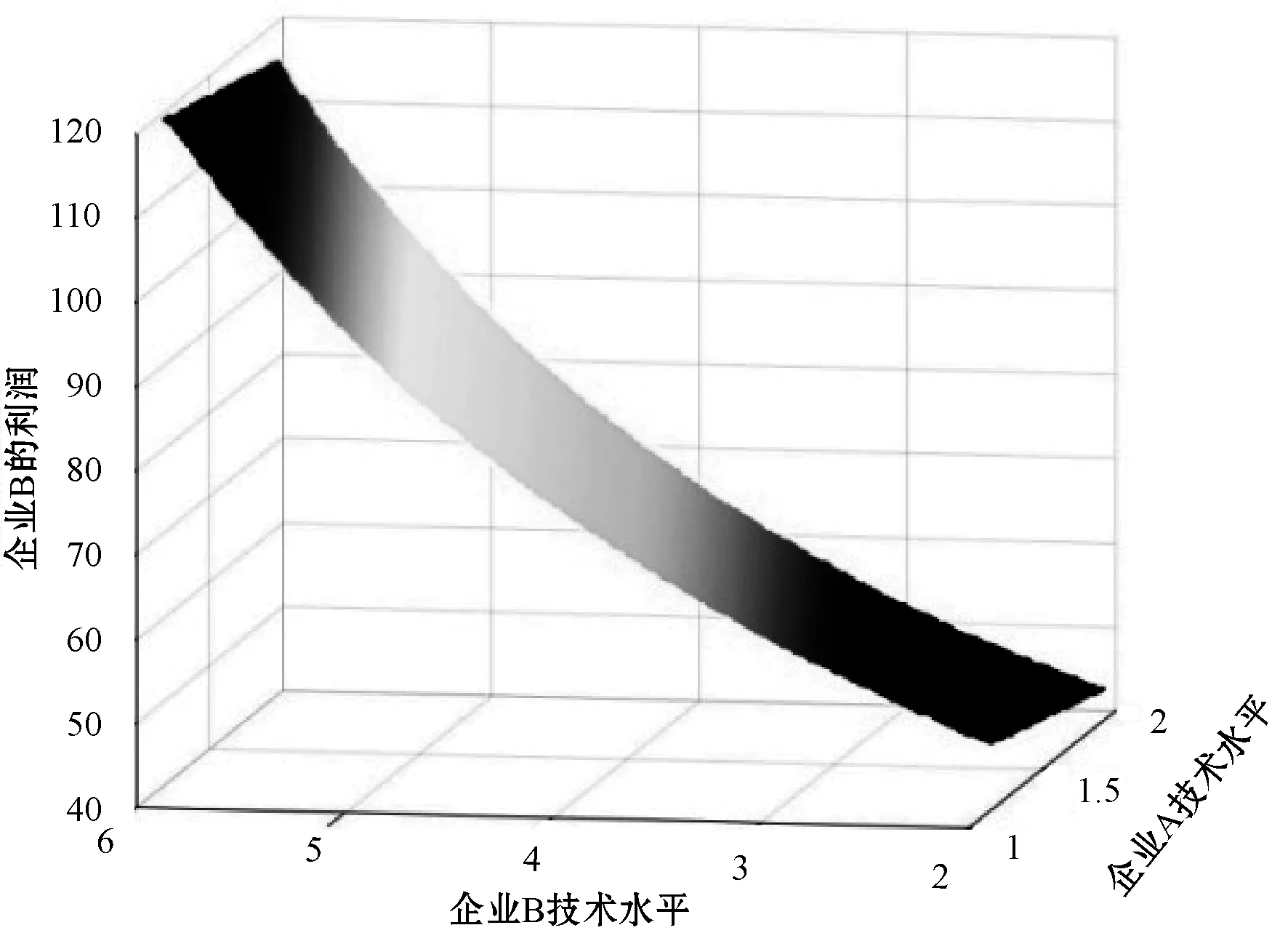
4 结 语
