残余应力对Oliver-Pharr方法测量弹性模量的影响

常 超, 高亮亮, 叶启华

(1.太原科技大学 应用科学学院， 太原 030024； 2.晋城技师学院 自动化工程系， 晋城 048000； 3.广州柴油机厂股份有限公司， 广州 510380)

随着微机电系统(MEMS)的发展，材料在微、纳米尺度下的力学性能受到国内外研究人员的广泛关注[1]。纳米压痕技术作为一种高分辨率的无损检测技术，具有试样制备简单、非破坏性等特点，主要用来测量材料的硬度、弹性模量及塑性等力学性能[2-5]。 Oliver-Pharr方法是利用纳米压痕测量材料弹性模量最常用的方法，但在制备纳米压痕试样过程中的研磨和抛光过程会对材料表面产生表面应力。笔者利用数值模拟分析对试样分别加载拉、压两种不同应力，研究拉、压不同应力状态对Oliver-Pharr模型测量弹性模量的影响。

1 纳米压痕测量弹性模量的力学方法

纳米压痕试验是通过不同的试验力学模型对不同的力学响应进行分析得到被测材料的参数。目前纳米压痕试验主要采用Oliver-Pharr方法测量杨氏模量[6]。

采用纳米压痕试验所得的载荷-位移曲线进行分析，Oliver-Pharr方法认为在卸载初始阶段材料发生了弹性变形

(1)

式中：Er为简约模量;β是与压头几何形状有关的常数，玻氏压头β=1.034；S为接触刚度；A为接触面积。

下式为简约模量Er和压头的弹性模量Ei、压头的泊松比νi反演出试样的压入弹性模量EIT。

(2)

式中：ν是试样的泊松比。

常用幂函数形式来拟合卸载初始阶段的载荷-位移曲线

F=B(h-hp)b

(3)

式中：B和b均为拟合参数;h为压痕位移；hp为完全卸载后的残余深度。

对上式求导，并在压痕最大位移hm处取值，可计算出接触刚度S

(4)

接触面积函数A(hc)可通过压入接触深度hc拟合计算得到

(5)

式中：Ci为最佳拟合常数。

接触深度hc的计算式为

(6)

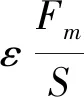
2 纳米压痕测量弹性模量的仿真模型

采用ABAQUS模拟软件建立纳米压痕压入测试模型，如图1所示。几何建模考虑到压头、试样的结构和载荷的对称性，可只选取对称模型建模；采用圆锥角为70.3°的圆锥压头近似代替Berkovich压头，压头尖端处设计为半径100 nm的圆弧[7]。金刚石压头为解析刚体模型，材料模型简化为完全弹塑性模型。铝合金材料的弹性模量为70 000 MPa，泊松比设置为0.3，屈服应力设置为300 MPa；石英材料的弹性模量为72 000 MPa，泊松比为0.17，屈服应力设置为5 500 MPa。网格单元采用CAX4R单元。考虑到压入过程中压头与被压材料应力集中，靠近压头采用较为密集的网格线，在较远的区域采用较大的网格线来进行划分。将材料下边界定义为完全固定，左边界定义x轴方向对称约束；对于试样存在不同的残余应力状态可通过对试样加载相应的外载荷来模拟，大小为100 MPa。

图1 纳米压痕有限元模型图Fig.1 Finite element model of nanoindentation: a) compressive stress state;b) meshing model

3 模拟结果与讨论

3.1 残余应力对材料加载、卸载曲线的影响

图2为石英材料和铝合金材料在不同残余应力状态下的载荷-位移曲线。在压痕深度相同时，若压痕附近表面的残余应力状态为压应力时，所对应的最大压入载荷大于同一压痕位置自然状态下的最大压入载荷；当压痕附近表面的残余应力状态为拉应力时，对应的最大压入载荷小于同一压痕位置自然状态下的最大压入载荷。

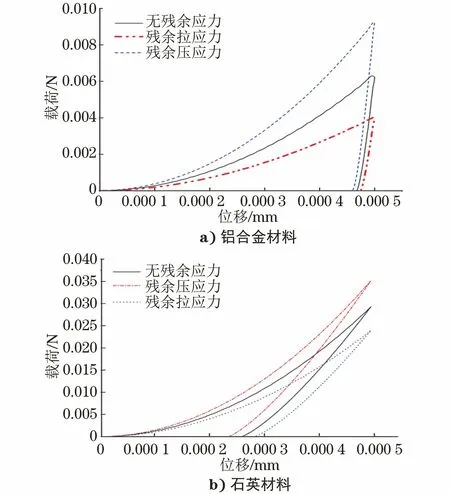
图2 铝合金材料和石英材料在不同残余应力 状态下的载荷-位移曲线Fig.2 Load-displacement curves of a) aluminum alloy material and b) fused silica material under different residual stress conditions

3.2 残余应力对铝合金材料弹性模量测量的影响

计算得到不同残余应力状态下铝合金材料的弹性模量，将其与铝合金材料原本的弹性模量比较，分析不同残余应力状态下Oliver-Pharr方法测量铝合金材料弹性模量所产生的误差，见表1。表1中数据表明，在没有残余应力时，对于铝合金材料使用Oliver-Pharr方法所测得的弹性模量相对于标准弹性模量产生的误差为14.7%；当残余应力为100 MPa拉应力时，利用Oliver-Pharr方法所测得的铝合金材料弹性模量相对于标准弹性模量产生的误差为7.8%；而当残余应力为-100 MPa压应力时，利用Oliver-Pharr方法所测得的铝合金材料弹性模量相对于标准弹性模量产生的误差为41.3%。pile-up突起现象会影响Oliver-Pharr方法测量弹性模量的结果，对于铝合金材料等塑性变形较大的金属材料，在压头压入过程中易产生pile-up突起现象，过高估计接触半径造成Oliver-Pharr方法测量结果偏大。但在残余拉应力作用下会减弱pile-up突起现象的影响，残余压应力会增强该突起现象的影响。

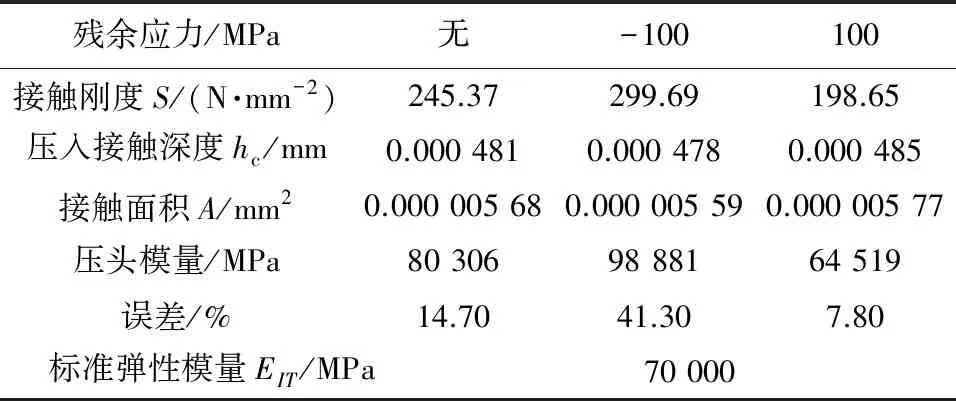
表1 不同残余应力对Oliver-Pharr方法测量铝合金 材料弹性模量的影响Tab.1 Effect of different residual stresses on elastic modulus of aluminum alloy material measured by Oliver-Pharr method

通过仿真结果直接得到接触深度的方式计算铝合金材料的弹性模量时(见表2)，在没有残余应力时，铝合金材料弹性模量估测结果相对于标准值的误差为1.8%；当残余应力为100 MPa拉应力时，铝合金材料弹性模量估测结果相对于标准值的误差0.9%；当残余应力为-100 MPa压应力时，铝合金材料弹性模量估测结果相对于标准值的误差0.7%。在3种应力状态下通过直接测量接触深度的方式计算铝合金材料的弹性模量其产生的误差较小。说明了残余应力会影响Oliver-Pharr方法估测接触深度，从而产生测试误差。

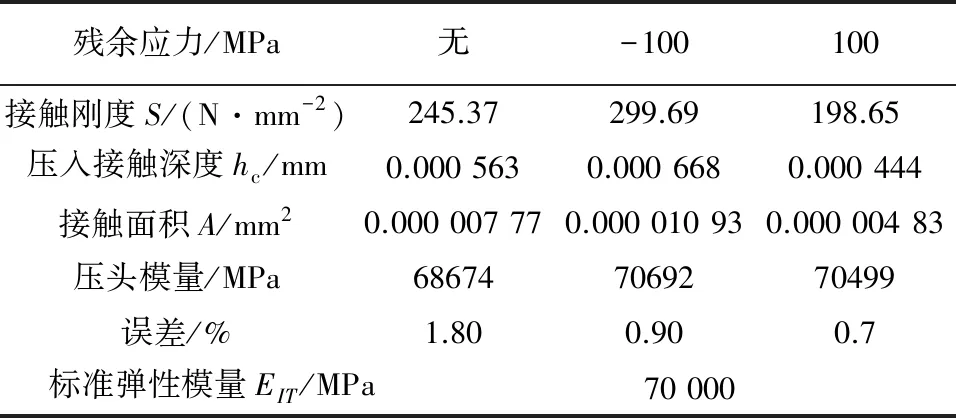
表2 不同残余应力对真实接触深度方法测量 铝合金材料弹性模量的影响Tab.2 Effect of different residual stresses on elastic modulus of aluminum alloy material measured by true contact depth method

3.3 残余应力对石英材料弹性模量测量的影响

利用Oliver-Pharr方法标定的石英材料作为对比分析的对象，由有限元软件仿真模拟得到石英材料的载荷-位移曲线[图2a)]，然后用Oliver-Pharr方法计算试样的压入弹性模量，得到表3的结果。

通过表3中的数据分析可知，没有残余应力时使用Oliver-Phar方法所测得的弹性模量和标准弹性模量相差甚微,误差仅为0.9%，此结果验证了Oliver-Pharr方法将石英材料作为标定材料的准确性；当残余应力为-100 MPa压应力时，所测得的弹性模量相对于标准弹性模量误差为14.7%；当残余应力为100 MPa拉应力时，所测得的弹性模量相对于标准弹性模量误差为11.9%。试验结果表明，残余应力对Oliver-Phar方法测量石英材料的弹性模量有相当的影响，使得石英材料作为测量材料弹性模量所标定的材料也不再适用。

表3 不同残余应力对Oliver-Pharr方法测量石英材料弹性模量的影响Tab.3 Effect of different residual stresses on elastic modulus of fused silica material measured by Oliver-Pharr method

对比通过实际测量接触深度求得弹性模量(表4)发现,无残余应力情况下测得的弹性模量与标准的弹性模量有4.6%的误差；当残余应力为-100 MPa压应力时，所测得的弹性模量对比于标准弹性模量误差为4.5%；而当残余应力为100 MPa拉应力时，所测得的弹性模量相对于标准弹性模量误差为4.7%。相比之下，在残余应力的影响下通过Oliver-Pharr方法测得的弹性模量有较大误差，进一步说明残余应力对Oliver-Pharr方法测量弹性模量的影响较大。

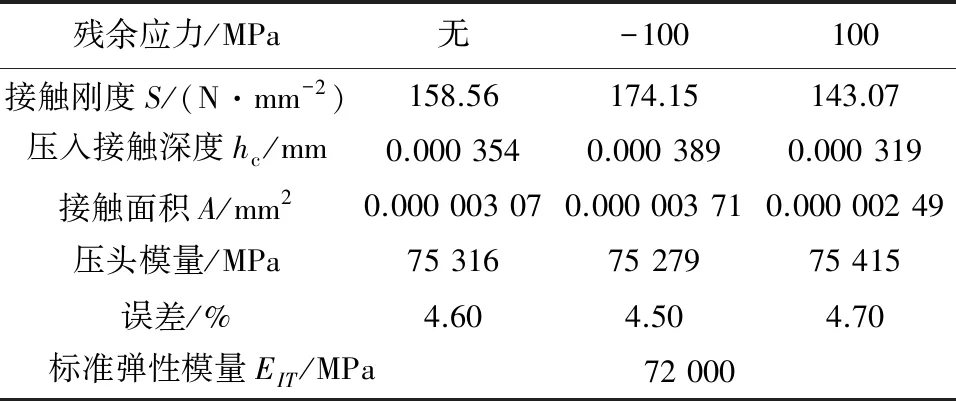
表4 不同残余应力对真实接触深度方法测量铝合金 材料弹性模量的影响Tab.4 Effect of different residual stresses on elastic modulus of fused silica material measured by true contact depth method

4 结论

(1) 残余应力对用Oliver-Pharr方法测量铝合金材料和石英材料的弹性模量都会产生很大的误差，表明Oliver-Pharr方法不适用于在有残余应力的情况下用来测量铝合金材料和石英材料的弹性模量。

(2) 铝合金材料在压头压入过程中出现的pile-up现象是测量材料铝合金弹性模量过程中影响Oliver-Pharr方法精确度的主要因素，残余应力也是通过影响这种现象中接触深度的测量和接触刚度的计算来影响Oliver-Pharr方法的精确度。

(3) 使用纳米压痕法测量材料弹性模量时应充分考虑残余应力的影响,测量不同材料的弹性模量应选用不同的方法。