不同连接属性下低桩承台重力式码头动力特性

周 丹，王多银，赵大淮，段伦良

(重庆交通大学 河海学院，重庆400074)

随着库区水位的日渐升高，地基条件良好的码头岸线越来越少，部分码头不得不修建在极端地基上[1]。重力式码头因施工相对简单、成本相对低廉、适应性强等优点而得到广泛应用[2]。桩-土-承台协同发挥作用过程中，桩侧土体出现的成拱效应有效改善地基承载力[3]，因此在深水区桥梁码头等工程中应用十分广泛[4-5]。低桩承台重力式码头兼有桩基和重力式码头的优点，能很好地适用于内河软土地区码头的建设。近年来国内外历次地震灾害调查结果[6-7]表明：码头在地震作用下极易遭到破坏，从而造成巨大经济损失。因此研究低桩承台重力式码头在地震作用下的动力响应的重要性不言而喻。

重力式码头与基础之间以摩擦接触的方式进行连接，建筑和桥梁中桩基-承台与上部结构则采用刚性连接，即锚固连接。为便于描述，将重力式码头称为上部结构，将桩-承台结构称为下部结构。地震作用下，低桩承台重力式码头上下部结构连接节点的工作形态直接影响码头整体结构安全性能。目前还没有低桩承台重力式码头上下部结构中采用锚固连接的相关研究，本文在低桩承台重力式码头上下部结构之间分别采用锚固连接和摩擦接触连接(图1)，利用ABAQUS有限元软件对两种连接方式形成的低桩承台重力式码头整体结构建立有限元模型，在地震荷载作用下进行动力时程分析，来探讨不同连接属性对结构动力响应的影响，为今后该种结构的抗震设计提供参考。

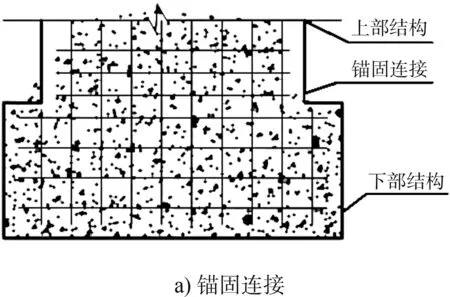
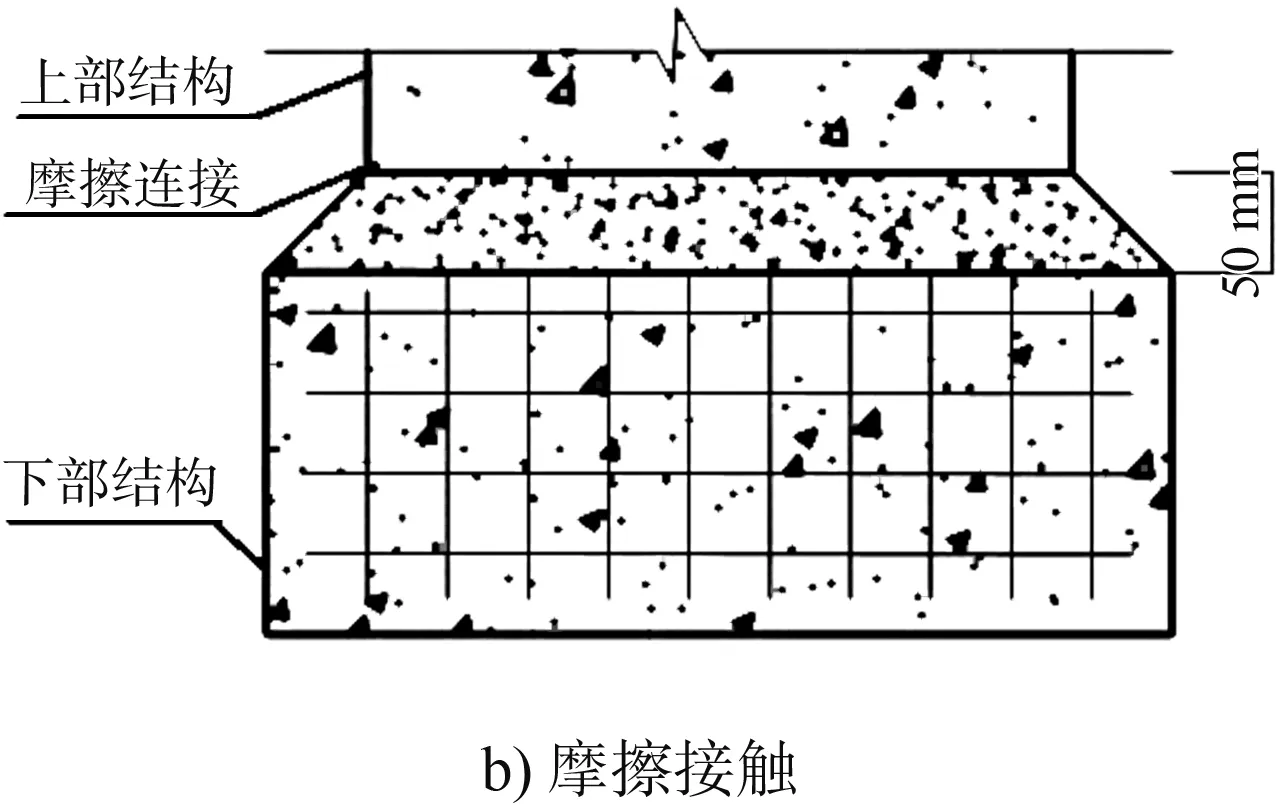
图1 锚固连接与摩擦接触连接

1 分析方法与求解

1.1 动力平衡方程的建立

根据平衡条件，建立低桩承台重力式码头结构在地震作用下的平衡方程[8]：

(1)

1.2 动力平衡方程的求解

求解动力平衡方程的基本方法有：时域分析法、频域分析法和振型叠加法，在数值分析中常采用振型叠加法和直接积分法，本文采用基于New-mark法的隐式积分法[9]：

(2)

(3)

(4)

(5)

(6)

(7)

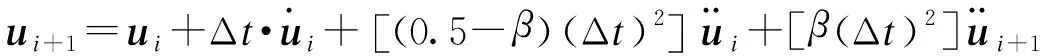
(8)

2 有限元模型的建立

2.1 工程概况

某500吨级的低桩-承台块体阶梯型结构重力式码头，所处场地为8度地震烈度带，主要建筑物等级为一级，该码头设计高水位为6.245 m，设计低水位为4.300 m；码头所处位置地势陡峭，其地基土土层由下至上分别为页岩、黏土和回填土。取沿河向长度3.5 m进行研究，承台底宽3.5 m、高1.8 m，胸墙高2 m，采用两桩承台重力式码头结构，桩径D为500 mm。结构断面见图2。

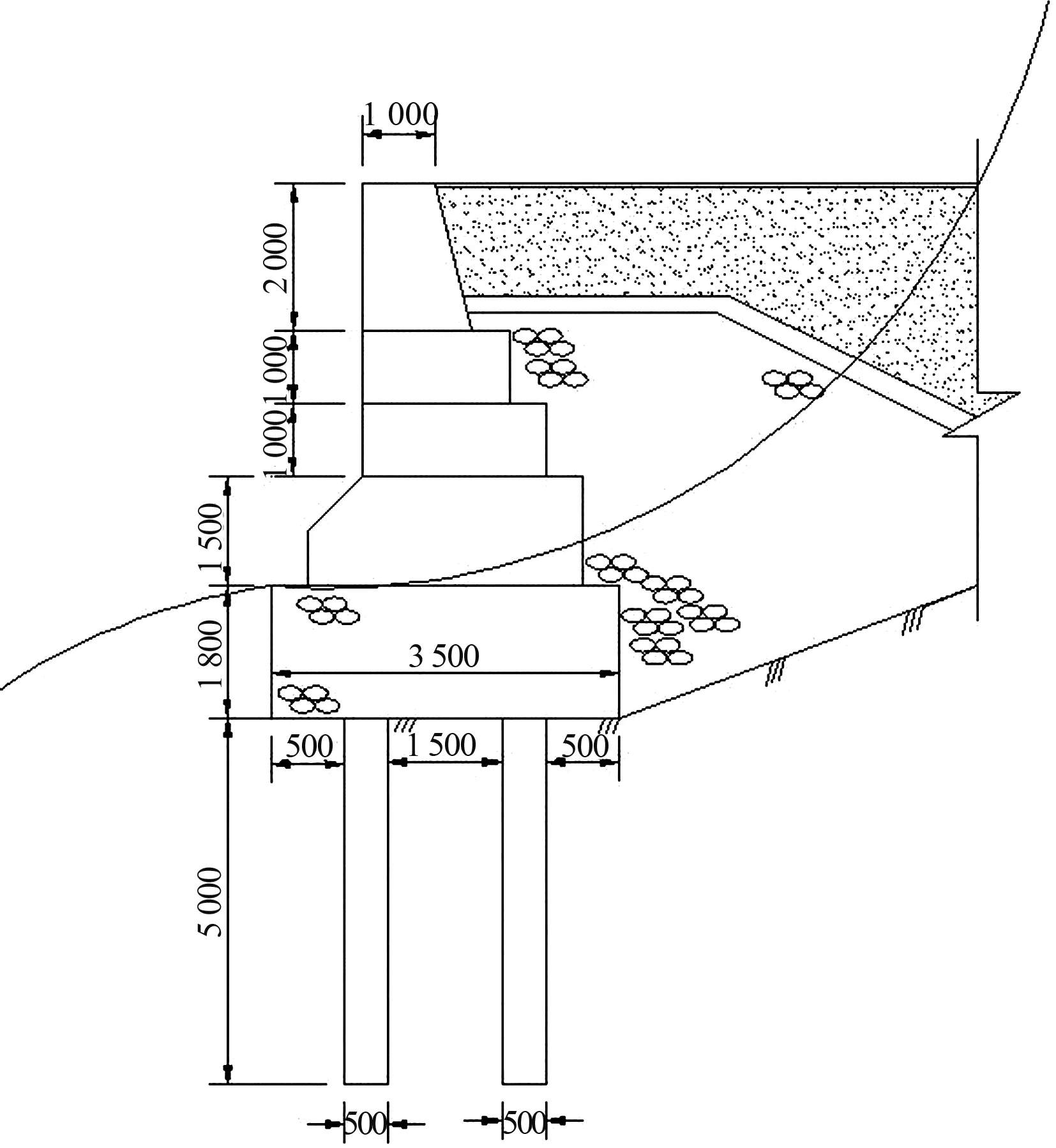
图2 结构断面(单位：mm)

2.2 有限元模型及相关参数

根据实际工程建立同尺寸的三维低桩承台重力式码头结构-土有限元模型，下部为地基土，桩底嵌入页岩，块体码头后为回填土。本文取桩轴外半径12D以内的土体、取桩端以下厚15D的地基土进行研究[10]。模型设计的材料相关参数见表1。

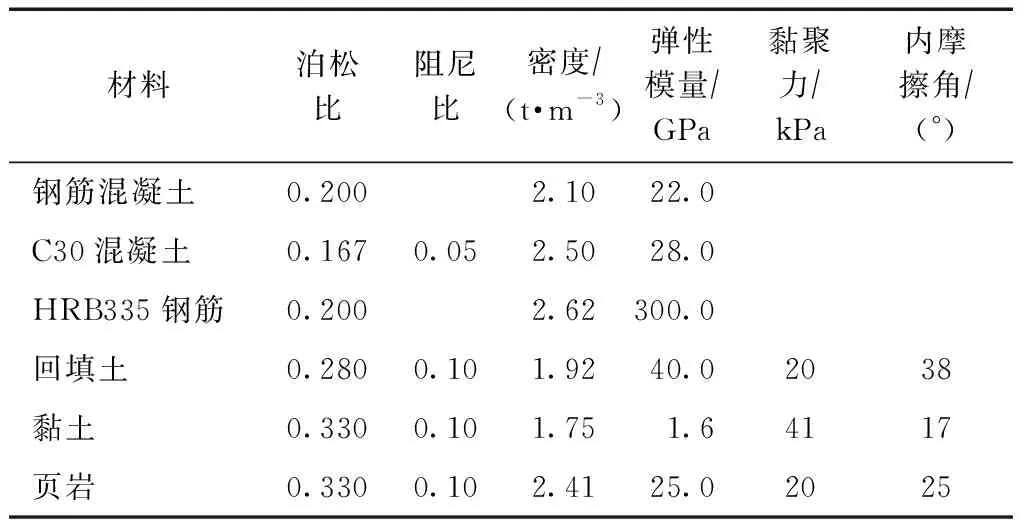
表1 模型参数

模型中重力式码头采用钢筋混凝土结构，桩基采用钢筋混凝土结构，按构造配筋。计算模型中混凝土采用塑性损伤模型[11]，地基土与回填土选用Mohr-Coulom塑性模型[12-13]，钢筋采用线弹性模型[14]。结构与土之间的接触部位存在滑移或脱开等现象，属于非线性问题，在ABAQUS中通过“接触对” 实现；钢筋与混凝土分别采用不同的单元分离建模，之后进行自由度耦合。

模型荷载中水上土体按照天然密度考虑，水下土体按照饱和密度考虑，水压力按静水压力考虑，地震荷载加速度时程曲线见图3。地基在未受到扰动时就存在天然应力，对分析过程产生了影响，因此本文采用自动平衡，即在step模块中创建geostatic分析步进行初始应力平衡。考虑桩-土-承台共同受力[15]，建立码头结构与土体有限元模型，见图4。

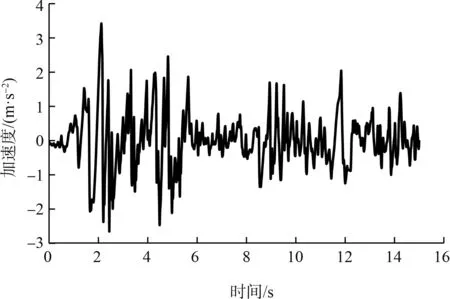
图3 0.2g EL-Centro波加速度时程曲线

图4 码头-土体有限元模型

3 不同上下部结构连接属性对结构动力响应的影响

3.1 结构水平动位移响应

通过ABAQUS精细化建模，得到两种连接属性对结构水平动位移影响规律，见图5及表2。由图5可知，在地震作用下，两种连接属性所对应的上下部结构水平动位移的变化趋势基本一致，且上部结构的水平动位移始终大于下部结构；在地震过程中，采用摩擦接触和锚固连接所对应结构水平动位移的最大值分别为-5.1、-3.6 mm，地震结束时，两种连接属性所对应结构的残余位移分别为-1.7、-1.2 mm。

由表2可知，在地震荷载作用下，采用摩擦接触连接的低桩承台重力式码头上下部结构水平动位移之差的最大值、重力式码头顶部与底部水平动位移之差的最大值及在地震结束时的残余水平动位移之差均比采用锚固连接时大。

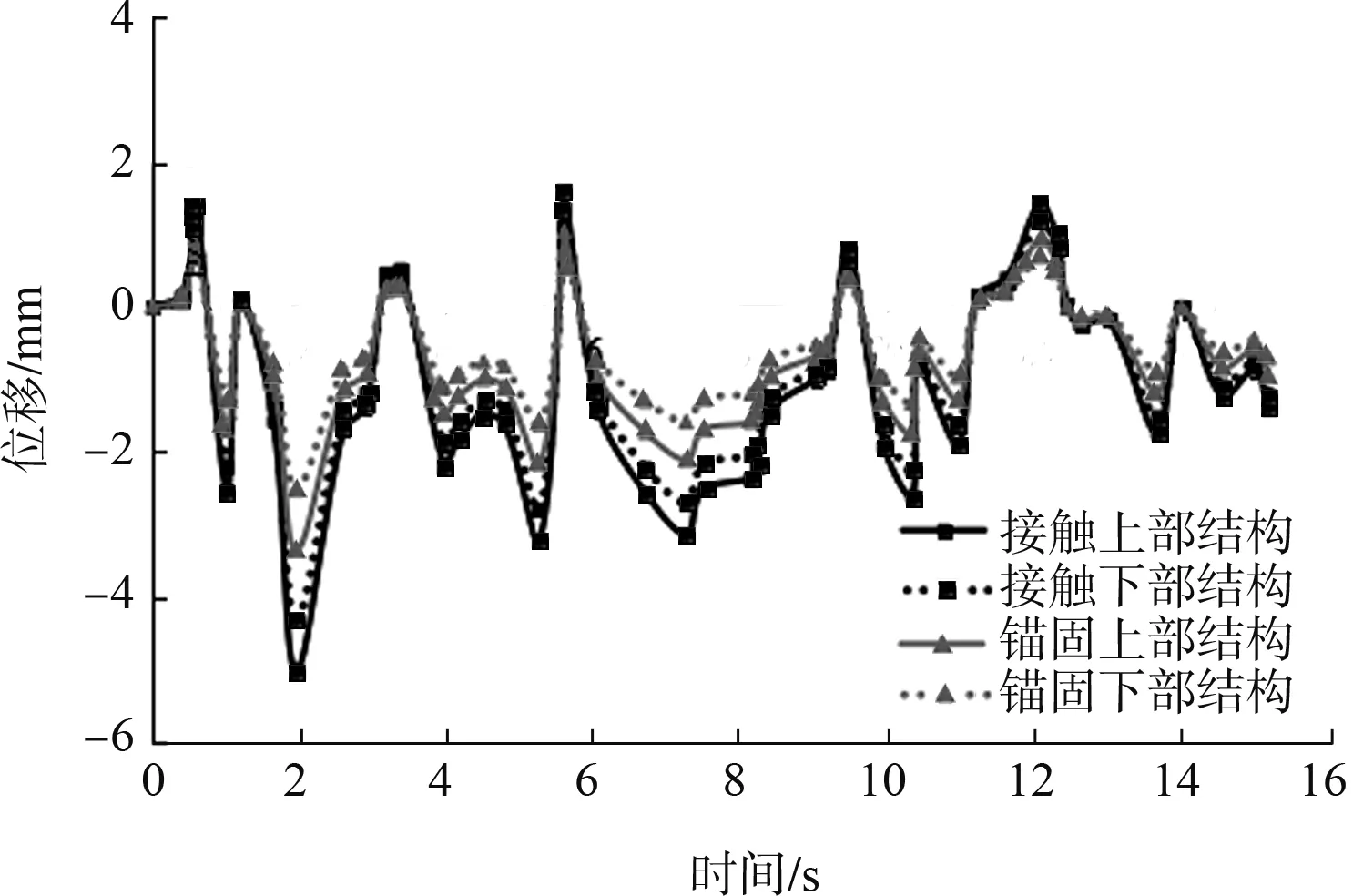
图5 上下部结构水平动位移最大值时程曲线

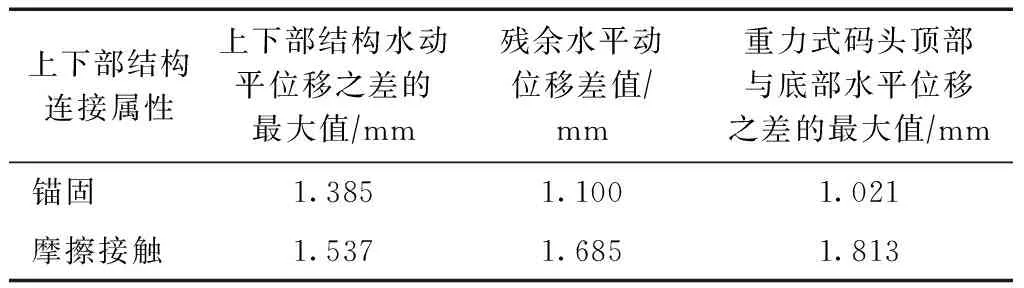
表2 上下部结构水平位移差值

3.2 结构水平加速度响应

两种连接属性对结构水平加速度的影响规律见图6及表3。

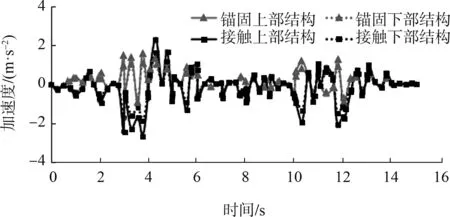
图6 上下部结构水平峰值加速度时程曲线

表3 上下部结构峰值加速度绝对值之差

由图6可知，在地震作用下，两种连接属性所对应的上下部结构的水平加速度随时间的变化趋势基本一致，且上部结构水平加速度绝对值均大于下部结构；由于地震响应的迟滞性，上下部结构达到峰值水平加速度的时间点均稍晚于输入地震荷载峰值加速度的时间点；在地震结束时，上下部结构的水平加速度都趋于0。

由表3可知，摩擦接触连接的结构达到峰值加速度的时间点晚于采用锚固连接结构；摩擦接触连接所对应的上下部结构水平加速度之差的最大值比采用锚固连接结构大；锚固连接所对应的上部结构峰值加速度占输入地震荷载加速度峰值的比率比摩擦接触连接结构大。这都是由于采用锚固连接结构的整体性要好于摩擦接触连接的结构。

3.3 结构应力响应

两种连接方式对低桩承台重力式码头结构应力响应的影响规律见图7～11及表4。

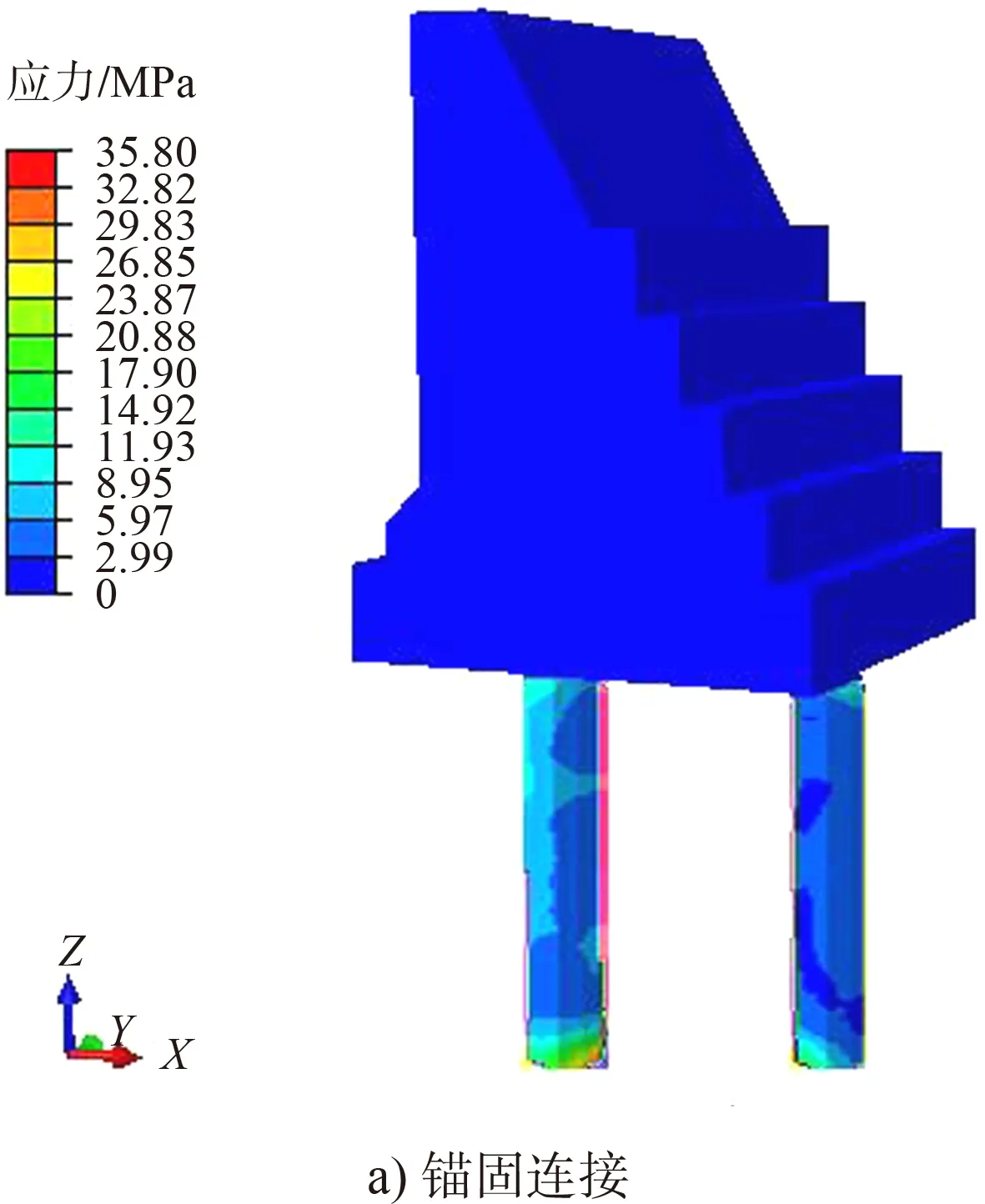
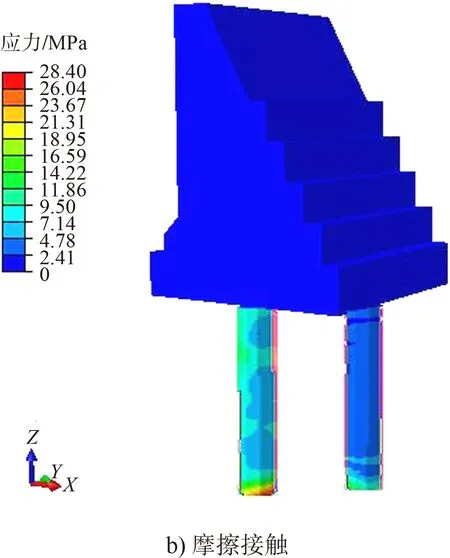
图7 结构应力云图

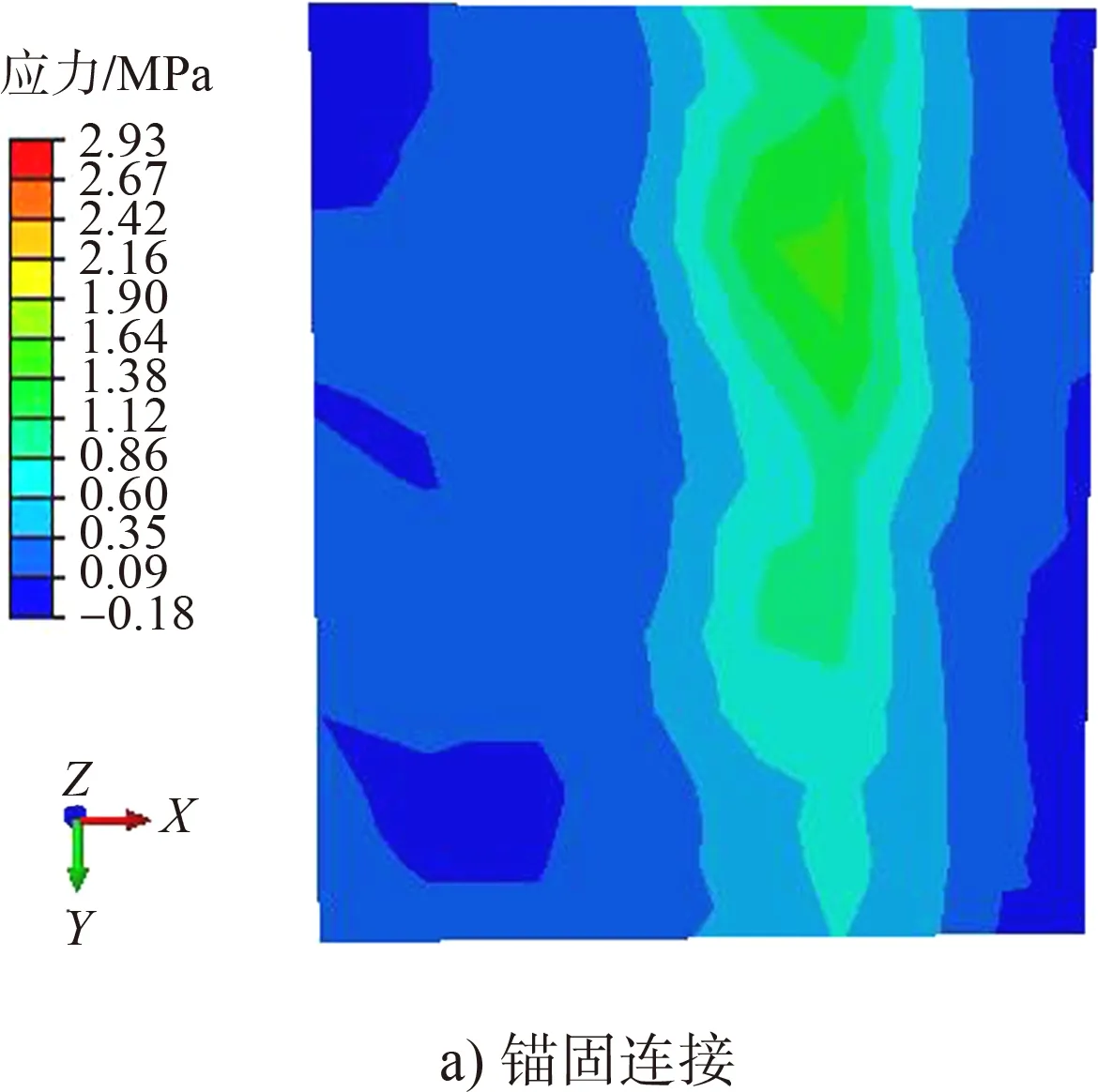
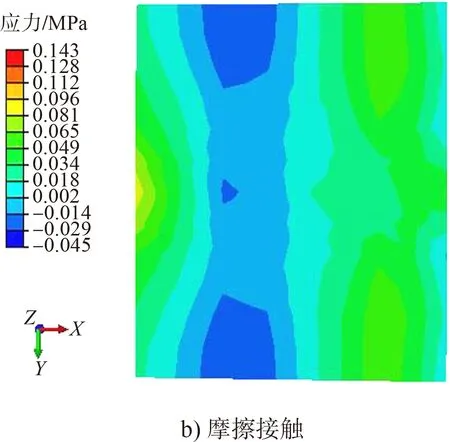
图8 码头底面拉应力云图

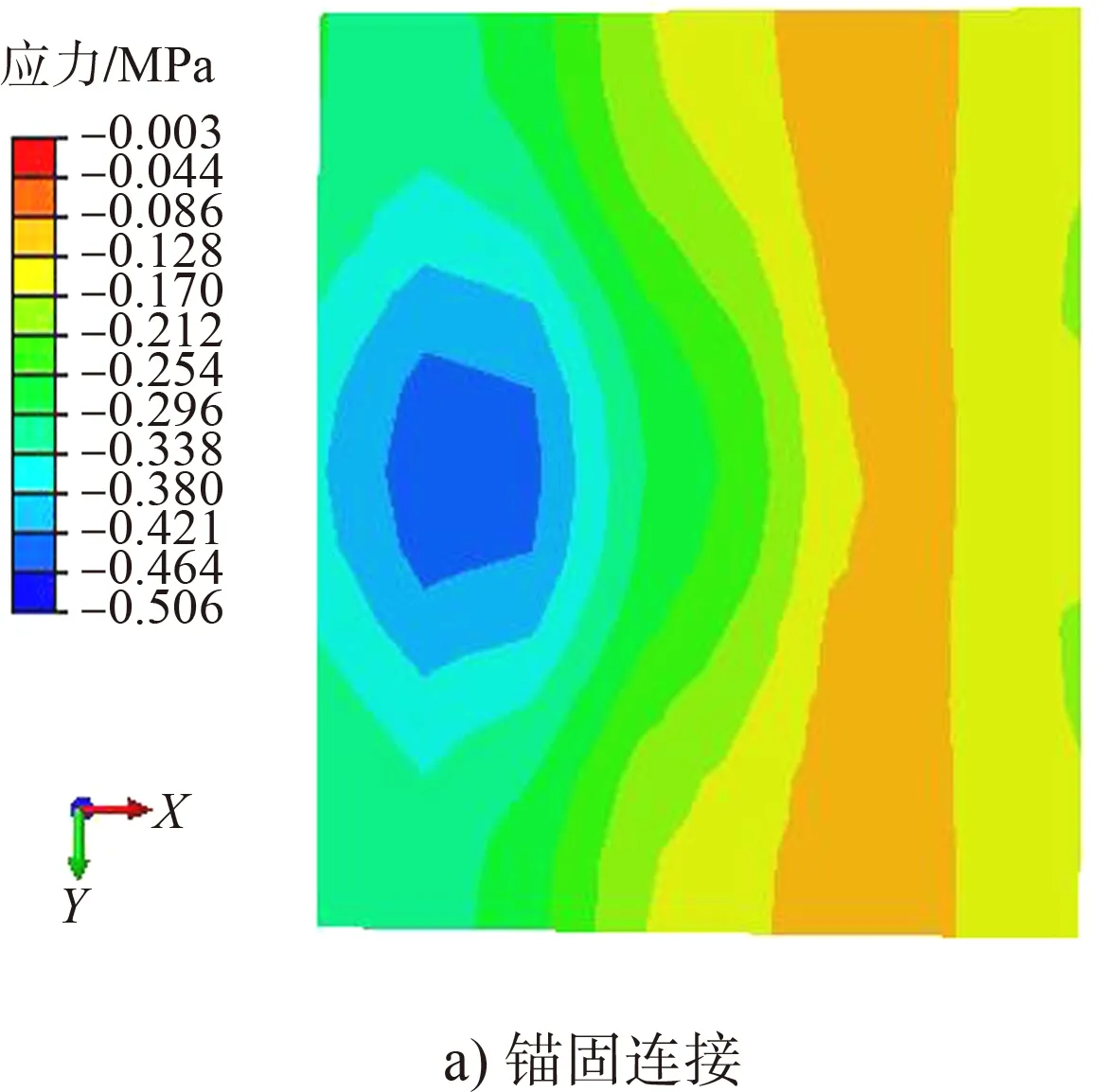
图9 码头底面压应力云图

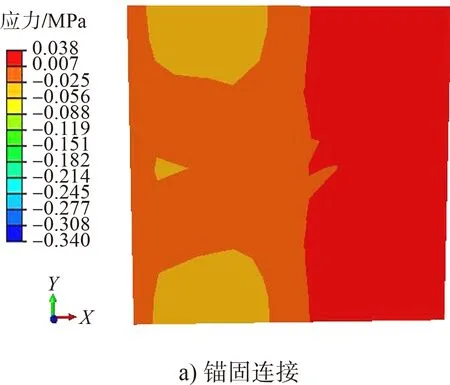
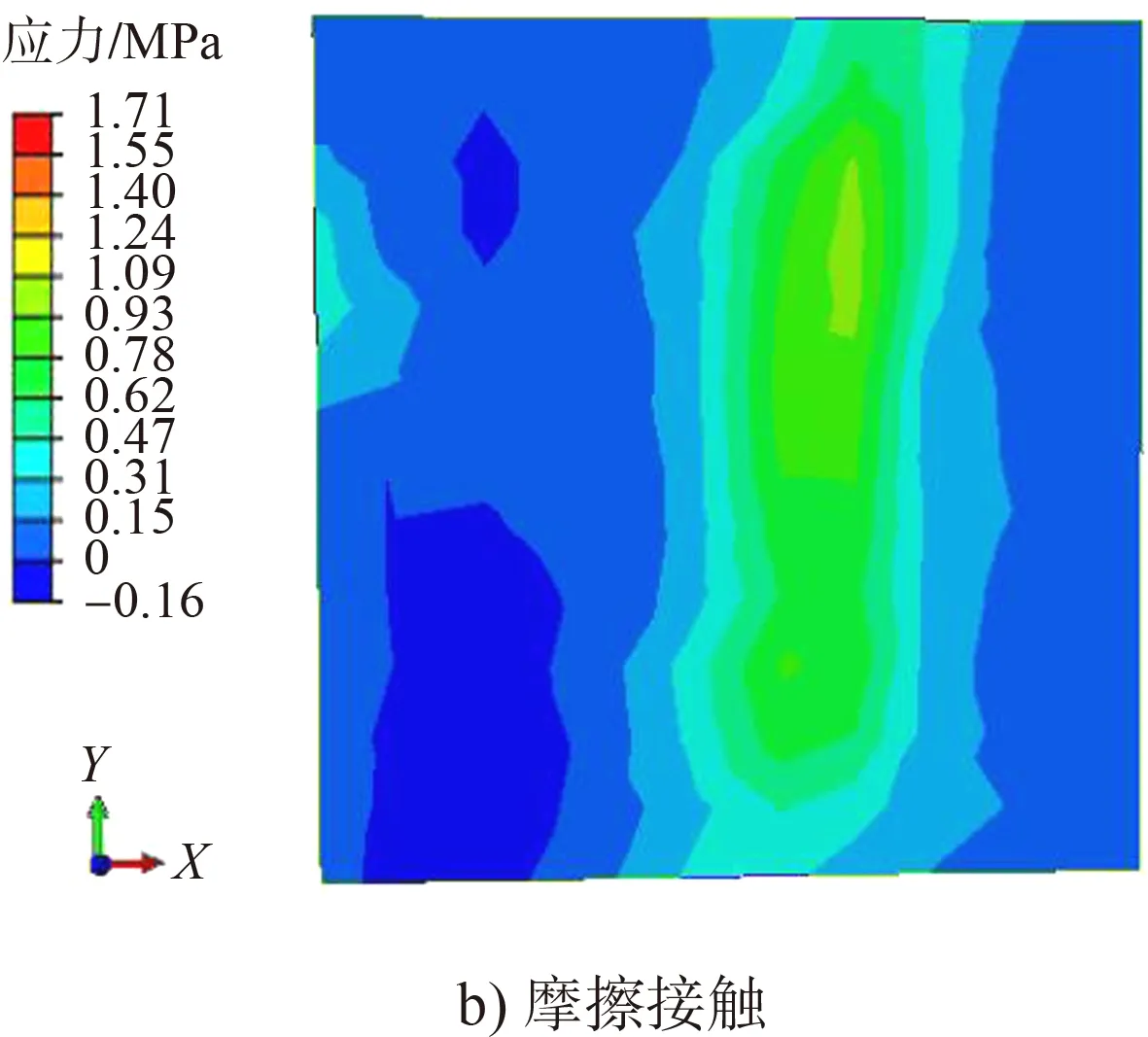
图10 承台顶面拉应力云图

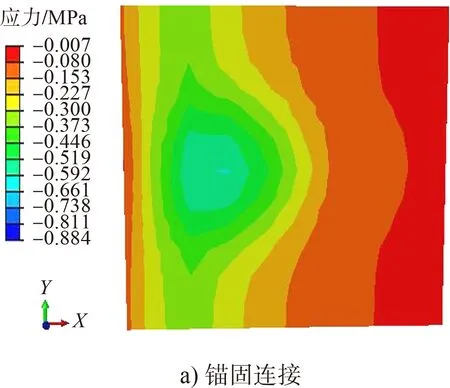
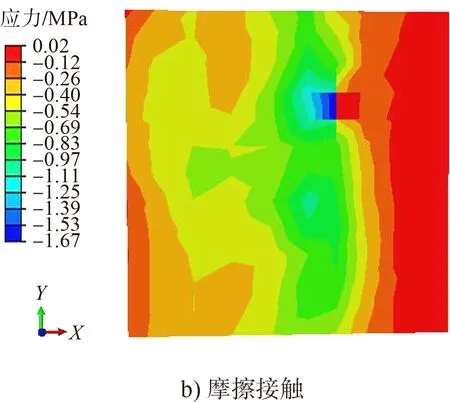
图11 承台顶面压应力云图

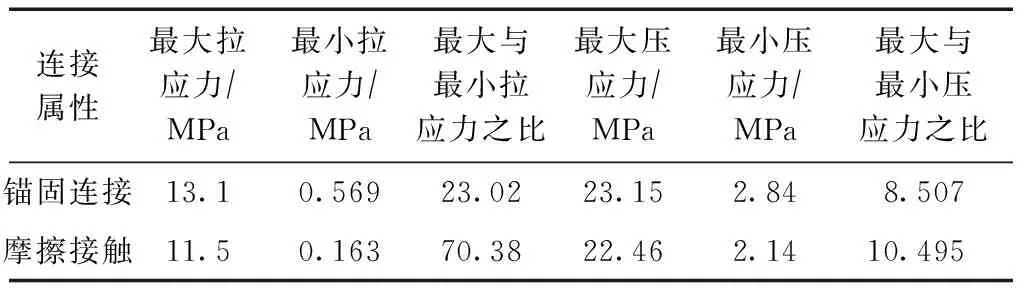
表4 上下部结构峰值应力及其比值

由图7可知，两种连接方式所对应结构整体应力都随高度的增加而减小；下部结构的应力都大于上部结构，桩身应力分布不均匀且桩底部应力最大。由图8、9可知，在地震荷载作用下，两种连接属性所对应的重力式码头底面的拉应力均沿河流方向呈带状分布，且锚固连接重力式码头底面的应力最大值较摩擦接触结构大；锚固连接所对应的重力式码头底面的压应力分布出现一定的集中现象，而摩擦接触所对应的重力式码头底面的压应力分布较分散。由图10、11可知，摩擦接触所对应的结构承台顶面的峰值拉压应力均小于锚固连接所对应的结构，这也是由于摩擦接触能在一定程度上缓解应力集中所致。

由表4可知，由于锚固连接应力传递效率明显好于摩擦接触连接属性，使得锚固连接所对应结构的最大、最小拉(压)应力均大于摩擦接触连接属性所对应的结构，且锚固连接所对应结构的最大与最小拉应力之比及最大与最小压应力之比均大于摩擦接触连接属性所对应的结构。

3.4 结构动土压力响应

两种连接属性对结构动土压力响应影响见图12、13及表5。

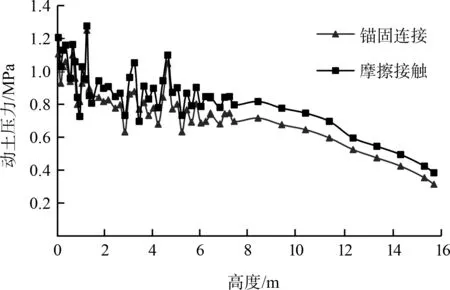
图12 结构动土压力沿高度变化曲线

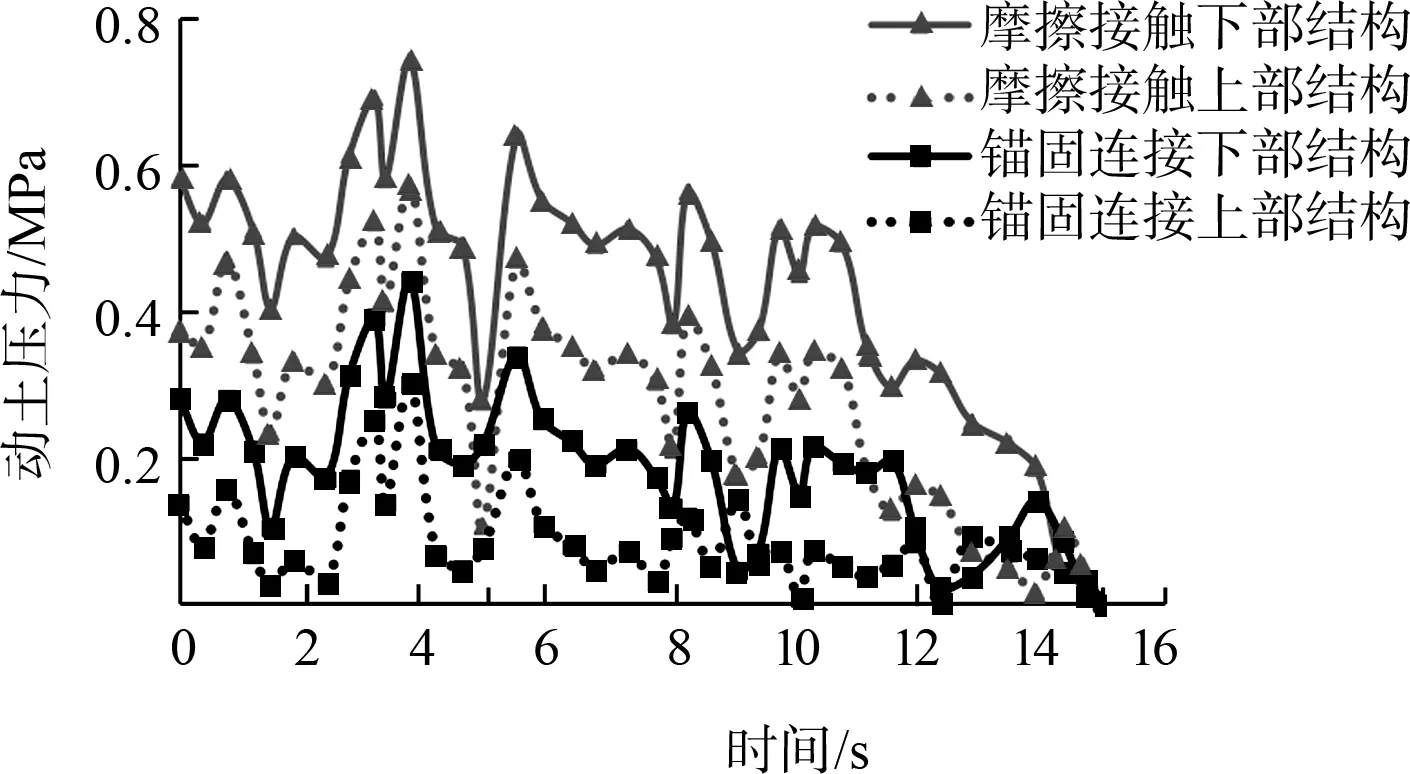
图13 上下部结构动土压力最大值时程曲线

表5 上下部结构动土压力及其比值

由图12可知，两种连接属性所对应的结构沿高度方向的动土压力均呈先振荡减小再线性减小趋势；锚固连接所对应的结构沿结构高度方向的动土压力始终小于摩擦接触所对应的结构。由图13可知，两种连接属性所对应上下部结构动土压力随时间的变化趋势基本一致，下部结构的动土压力均大于上部结构。

由表5可知，两种连接属性所对应的下部结构的峰值动土压力均大于上部结构，摩擦接触所对应的上下部结构最大动土压力值、最大与最小动土压力之比均大于锚固连接结构，这说明，摩擦接触连接所对应的结构在地震荷载作用下更容易发生应力集中现象。

4 结论

1)两种连接属性所对应结构的水平动位移，其上下部结构变化趋势基本一致，都随结构高度增加逐渐增大，且上部结构始终大于下部结构；在地震结束时，锚固连接所对应结构的残余位移比摩擦接触结构小。

2)两种连接属性所对应结构的水平加速度绝对值，都随高度的增加而增大，上部结构均大于下部结构；摩擦接触所对应的结构达到峰值加速度的时间点明显滞后于锚固连接结构，摩擦接触所对应结构的上下部结构水平峰值加速度之差大于采用锚固连接属性的结构；锚固连接所对应的上部结构峰值加速度占输入地震荷载加速度峰值的比率大于采用摩擦接触连接的结构。

3)锚固连接所对应的重力式码头底面的峰值拉、压应力及承台顶面的峰值拉、压应力均大于摩擦接触连接所对应的结构；锚固连接所对应结构的最大与最小拉(压)应力均小于摩擦接触连接属性所对应的结构。

4)两种连接属性所对应上下部结构的动土压力沿结构高度均呈先振荡减小再线性减小趋势，锚固连接所对应的结构沿结构高度方向的动土压力始终小于摩擦接触所对应的结构；摩擦接触所对应的上下部结构最大动土压力值、最大与最小动土压力之比均大于锚固连接结构。