非90o移相器的实现及在通信系统中的应用

刘渭清 张馨予

（西安文理学院 信息工程学院，陕西 西安710065）

0 引言

非90o移相器（FHT）也称为小数移相器，它是相对于90o移相器而提出的一个新概念，主要用于对信号进行小数阶移相，例如移相0.234 rad。在模拟技术中难以实现如此高精度移相要求，而利用数字系统则可较好地完成对信号进行高精度移相。目前，小数移相器已经在实践中获得了越来越多的应用，例如图像的边缘检测方面等。

1 小数移相器（FHT）的定义

1.1 理想FHT的频率响应函数[1]

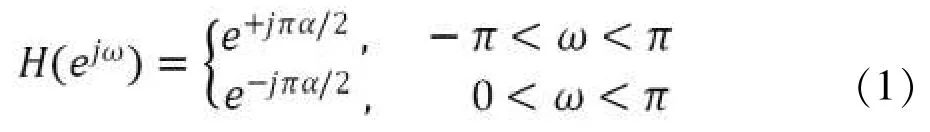
其中，尺度因子α是一个指定的参数，且0＜α＜1。

其相位响应如图（1）所示。

图1 理想小数移相器的相位响应（α=0.8）

1.2 非理想FHT的频率响应函数

其中，尺度因子α的作用同式（1）。其相位响应如图2所示。

图2 指定通带宽度的FHT的相位响应

由定义可知，FHT可以看成是满足相位要求的全通滤波器，其幅度恒为1。因此，小数移相器（FHT）主要用来实现对信号进行高精度移相且保持其幅度不变。

2 小数移相器（FHT）的设计及检验

2.1 设计满足指标的FHT

根据文献[1]所给出的设计方法，若给定技术指标ωa=0.2π，ωb=0.8π，α=0.2，假定N=16。借助文献[2]的式（16）和式（11）可得所设计系统的系统函数，其相位响应如图3所示系统的移相值为π/2×α=0.314rad。若相位响应的精度不满足技术指标要求，可增大N，重新求解。

图3 设计的FHT的相位响应

2.2 系统的滤波效果检验

2.2.1给定实信号

x（n）=（0.5）nu（n），n=0，1，…，511

其相位响应如图4所示。以该信号作为输入，求所设计系统的输出，核心程序如下：

N=512; %信号采样点数

n=0:N-1;

x=0.5.^n; %信号

y=filter（b，a，x）; %计算系统输出，

%其中b，a是系统函数的分子和分母系数。

输出信号y的相位响应如图5所示。

图4 输入实信号的相位谱

图5 输出信号的相位谱

比较图4和图5，可以看出，系统对输入信号频率在范围内的部分做了移相，系统设计符合要求。

2.2.2给定一个复信号

x（n）=（0.9exp（jπ）/3））n，n=0，1，…511

其相位响应如图6所示。

图6 输入复信号的相位谱

以该信号作为输入，系统的输出如图7所示。比较图（6）和图（7），可以看出，系统对输入信号频率在0.2π～0.8π内的部分做了0.314 rad的移相，系统设计符合要求。因此，系统对实信号和复信号均适用。

图7 输出信号的相位谱

3 小数移相器（FHT）在通信系统中的应用

3.1 实信号的解析信号

小数移相器可用来构造单边带信号以节省通信时的带宽。若给定实信号x（n），其解析信号可表示为：

可以看出，解析信号是一个单边带信号，且与原实信号包含相同的信息。

3.2 调制与解调

根据FHT及其解析信号的特点，可以利用其构造一个加密的SSB通信系统，其调制原理如图8所示。

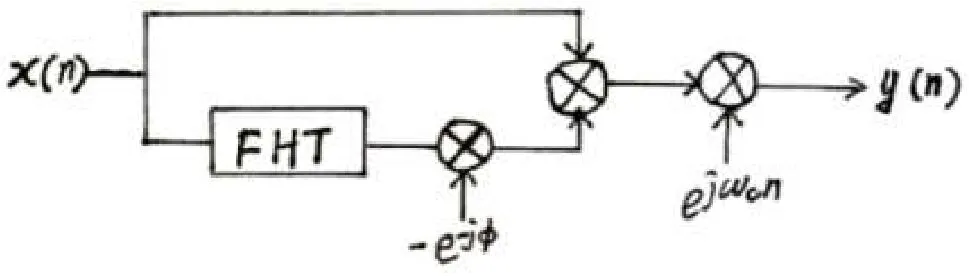
图8 调制器原理图

图8中的ωc是载波频率，是FHT的小数阶数。在系统中，阶数可以作为解调器的密钥，如果在解调过程中阶数未知，则无法从接收到的y（n）中恢复出x（n）。图8的调制原理：首先，产生实信号的解析信号；其次，用解析信号调制频率为ωc的正弦波，得到已调信号：

解调器的原理如图9所示，这里需要说明的是调制器的输出信号为，若给其乘以常数，使其成为，将式（3）带入，则可以证明：

Re[y（n）]=x（n）

据此可以得到图（9）所示的解调原理图。

图9 解调器原理图

4 结语

综上所述，本文介绍了一种小数移相器的实现方法并给出了检验程序，同时分析了FHT在构成加密的SSB系统中的应用。