广义线性指数混料模型的A—最优设计

陈博照 闫 湛

（1.广东白云学院 教育与体育学院，广东 广州510080；2.广州工商学院，广东 广州510000）

1 混料试验设计

混料配比问题，是工农业生产及生物制药等科学试验中经常遇到的多因素试验设计问题。实验者要通过尽可能少的试验次数得出各种配比成分的比例。如建筑房所用的混凝土，是将砂、碎石，以及若干种型号的水泥混合搅拌而成，人们要得到最好的黏合度与稳定性就必须经过重复的试验。怎样去设计这些试验使得试验成本低且精度高，从而得出一个适用于实际操作的回归方程呢？这就是混料试验设计的研究范畴。

混料问题中的可控变量，即每个因素对总体的影响都以它们在总量中所占的比例表现出来，也就是说研究的重点不在某些因素的量，而是这些因素的量在总量中所占的百分比[1]。假设：混料系统中共有q个因素， 第i个因素在总量中所占比例为xi，xi（i=1，2，…q），应满足：

这就是混料试验设计的基本约束条件。其中，将xi称为第i个混料分量。

2 A-最优准则

通过对各分量分配比重，可以得到一个初步设计。但在进行实操试验之前，必须先对这个设计进行相应的检验与评价，若草率的进行试验会导致资源浪费、成本增加。评价一个设计的依据就是最优准则，最优准则是衡量一个设计优劣程度的基本标准。经过不断地完善，现仍广泛使用的准则有D-最优、A-最优、R-最优等。其中，A-最优准则要求所有未知参数估计值的方差之和达到最小，其统计意义在于通过对各参数估计的置信区间长度的平方和的约束，来衡量估计的优劣[2]。这个出发点可以使模型的总体方差得到有效的控制，避免了出现某参数估计效率低下的情况，对置信椭球体的平均轴长有很好的制约作用。可以说，一个设计若能达到A-最优准则的要求，那么它在实际应用中对试验点的选取就能起到很好的引导作用。

3 广义线性混料模型

在混料模型的研究历程中，研究者从简单的线性模型、多项式模型、可加模型到非线性模型；从同方差模型到复杂的异方差模型；从常见的单响应模型、两响应模型到与实际联系密切的多响应模型，一步步的对模型进行深化与探索。模型的多样性、全面性已经让实验设计的适用范围更广泛[3]。在诸多模型中，q变量m阶Scheffé中心多项式模型可以说是混料模型的鼻祖，与之对应的变量阶单纯形—格子设计是一种非常优美的最优设计，对这个模型在各种最优准则下的研究也已经相当成熟。在此，将在前人的研究基础上提出一类广义线性混料模型，并对它在A-准则下的最优设计进行研究，作为对已有模型的补充。

q变量一阶广义指数线性混料模型：

这种模型属于q变量一阶广义线性模型中的一种，它在研究漂白剂、杀虫剂、混合杀毒药剂，甚至在化妆品的配方问题上都有很大的应用，下面将对广义指数模型的最优设计进行探讨。

4 一阶广义指数线性混料模型的A-最优设计

在q变量m阶Scheffé中心多项式模型中，常数项β0可以通过混料模型分量之和为1的特性分解到一阶项的系数中，常见的线性混料模型是不带常数项的，然而广义指数模型并不具备这种可分解的性质，因此对其最优设计的研究要困难得多。

对于2变量一阶广义指数线性混料模

固定模型的三个设计点， 分别为 （1，0），（0，1），先求解模型所对应的单纯形的各类中心点上的A-最优配置，然后再证明所得到的设计是该模型的A-最优设计。

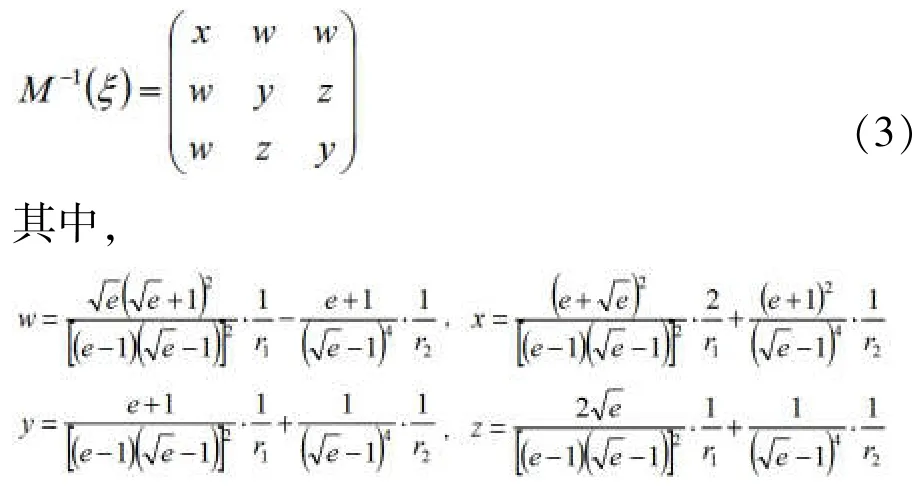
信息矩阵的逆的迹

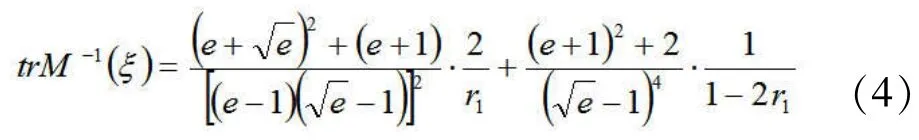
通过对上式进行最小化处理，可得：r1≈0.2377，r2≈0.5246

此时，信息矩阵逆的迹的最小值min[ t rM-1（）]≈324.653。所以，纯分量点上测度0.2377，二分量点上测度0.5246的配置就是设计点在三个中心点上的A-最优配置[5]。

接着，就得到的给定设计点的A-最优配置，往证设计：

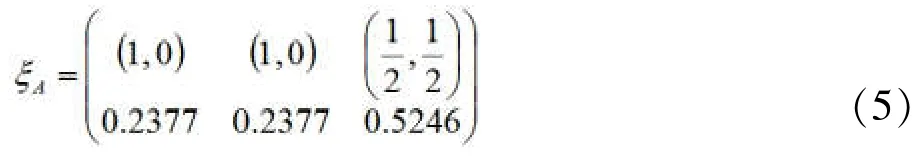
就是模型（2）的A-最优设计。

其中，a=x2+2w2，b=（x+y+z）w，c=w2+y2+z2，d=w2+2yz，再结合r1与r2的最优配置比例，可以得出设计的A-最优方差函数表达式：

在上式中，x1，x2必须满足混料基本条件x1+x2=1，故进一步通过消元求导可以得到当试验点分别取时，方差函数dA（x；）都能取得最大值324.653。因此，对试验区域内任一试验点都有：dA（x；）≤324.653。

5 总结

变量一阶广义指数线性混料模型最优设计的提出与证明，为此类模型的在实际应用过程中试验点的选取以及试验点的投入权重提供了一个明确的方向，三个试验点选在两个纯分量点上与二分量点上，测度分别为，与的试验，能避免参数估计过程中劣性参数的出现，从而得到一个行之有效的混料模型，可用于对未知响应的预测以及总体数据的评估。