Singer模型算法在目标跟踪中的应用研究
2020-11-10房晓丽陈玉敏方鑫钰
房晓丽 陈玉敏 方鑫钰

摘要:近些年来,导弹跟踪制导对雷达机动目标的精确跟踪提出了前所未有的挑战,如何实现杂波环境下机动目标的精确跟踪一直是个难点。文章建立了杂波环境下机动目标Singer运动模型,给出了滤波方程,仿真分析了基于Singer模型的机动目标跟踪效果和精度。仿真结果表明,Singer模型对机动目标跟踪具有较好的跟踪效果。
关键词:Singer模型;滤波;机动目标跟踪
中图分类号:TP311
文献标识码:A
文章编号:1009-3044(2020)27-0007-04
开放科学(资源服务)标识码(OSID):
1 背景
机动目标跟踪作为国防领域中的弹道导弹精确制导的关键技术,具有重要的研究前景。它在卫星及导弹防御系统、火力控制、跟踪与攻击、战场监视等方面均可发挥重大作用[1]。在民用方面,机动目标跟踪也发挥着举足轻重的作用,它主要应用于空中交通管制、航海及航空中的导航、机器人的道路规划等。
对机动目标跟踪效果的评估主要是通过建立机动目标动力学模型来实现的[2]。然而,由于机动目标在飞行或航行时经常会突然出现转向、变速等运动,具有很强的随机性、突发性,导致建立机动目标模型需要考虑的因素很多,准确建模相对困难。
目前,建立机动目标动力学模型的算法很多,主要有变维VD模型算法、输入估计IE算法、Singer模型算法以及以交互多模模型为主的多模型跟踪算法等[3-4]。本文采用Matlab仿真分析方法,基于Singer运动模型,在同一仿真战情下分析了机动目标的跟踪效果和跟踪精度。
2 Singer算法描述
假定目标进行平面运动,其运动方程可以描述为:
X(t)=FX(t)+Ga(t) (1)
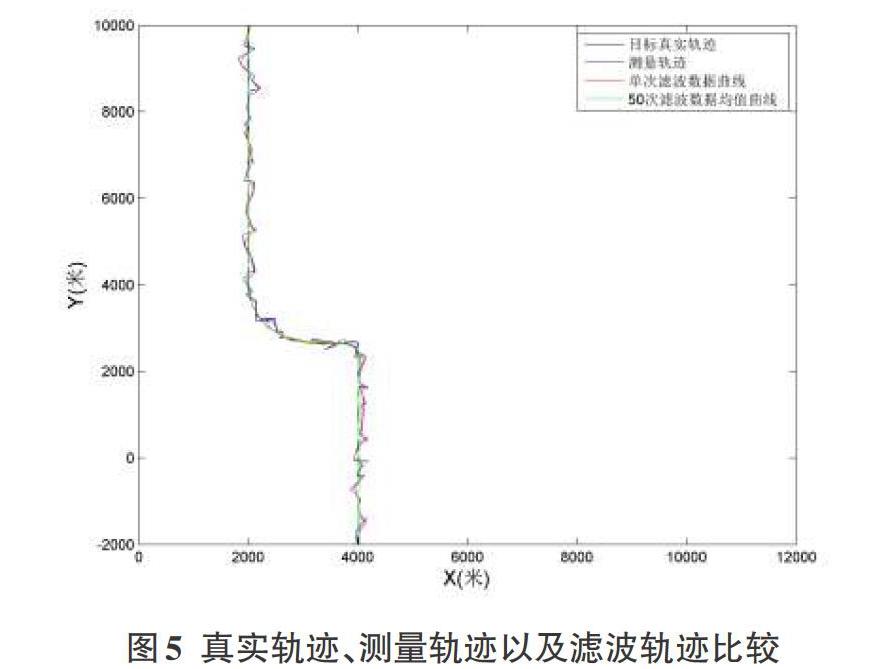
其中,a(t)为目标的加速度。对于跟踪系统,目标的机动性不可知,所以显而易见准确可靠地描述目标加速度是一个核心问题,smger算法把加速度a(t)看作一个平稳随机过程[5],其自相关函数为:真程序,利用蒙特卡罗方法对跟踪滤波器进行仿真分析[9-10],假定测试次数为50次,值得注意的是这里的次数假定,因为假定T的值为10s,测试次数即踩点次数为总时间除以T,所以为了满足条件我们选择了始终的50次。为了清晰观察目标的真实轨迹、测量轨迹以及滤波轨迹分别见图1至图4所示。
为了方便比较,把四条轨迹线绘制在一个图5中。可以看出,单次滤波曲线效果不是很理想,轨迹仍然有很大的波动,但是采用蒙特卡罗方法后[11],通过多次观测取均值,滤波效果较好。
同时,不难发现在目标匀加速过程中,Singer算法可以有效跟踪目标[12-13];在目标加速过程中,Singer算法跟踪效果并不是很好,特别是在加速度比较大时,比如该例子中的第二个转弯时,跟踪效果不理想。
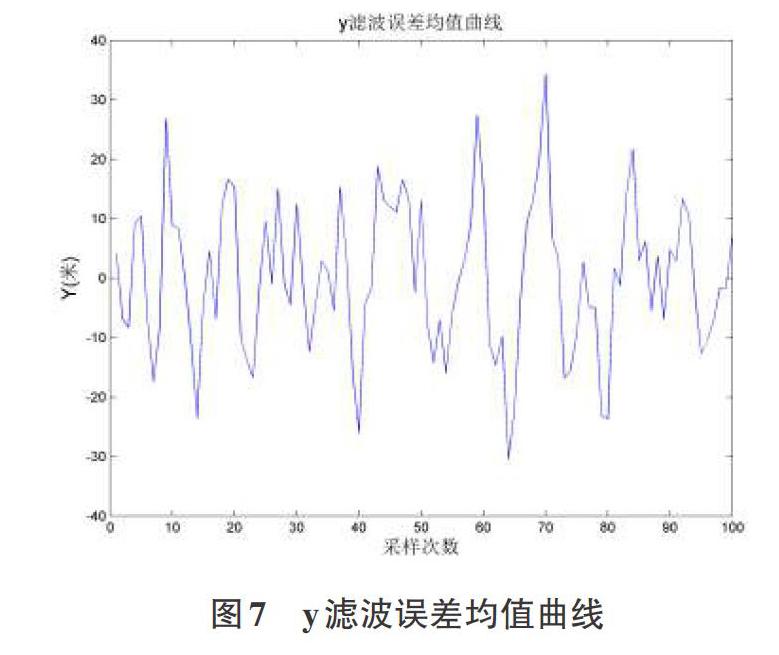
此外,X方向,Y方向滤波估计误差均值及误差标准差见实验图6至图9所示。由图并不能看出目标运动的特点,这也说明Singer算法虽然在多次滤波取均值的情况下效果较好,但是仍然有一定的局限性[14],误差比较大。
还可看出,图6和图7中在第二个转弯处相对较大的峰值体现了Singer算法对目标加速度较大过程中的跟踪效果不理想;而在匀速以及加速度较小时可以较好地跟踪目标,这跟图5中从轨迹中得出的结论是一致的。图8、图9可以看出,误差的标准差较大,误差起伏较大,说明该算法还具有一定的局限性。
5 结束语
本文从理论上推导了杂波条件下机动目标的Singer模型相关矩阵,从仿真方面分析了其相关特性。Singer算法模型在匀速或者加速度较小条件下可以良好的跟踪机动目标,在目标实施转弯,即加速度较大时跟踪效果一般,因此该方法在追踪转弯运动频繁的目标时有一定的局限性。
参考文献:
[1] Singer R A.Estimating optimal tracking filter performance formanned maneuvering targets[J]. IEEE Transactions on Aero-space and Electronic Systems, 1970, AES-6(4): 473-483.
[2]韓伟,黄晓斌,张燕.Singer模型下α-β-γ滤波的信息序列特性分析[J].计算机工程与应用,2013, 49(3): 156-158, 233.
[3]戚靖,刘成成,郭伟龙,等.一类基于改进的当前统计模型的目标跟踪算法研究[J].上海航天,2014, 31(2): 52-56.
[4]谭顺成,王国宏,王娜.lMM-Singer模型的机动目标跟踪算法[J].火力与指挥控制,2012, 37(2): 32-34.
[5]吴伟,王东进,陈卫东,密集杂波环境下多目标跟踪算法[J].现代雷达,2007, 29(2): 17-21,31.
[6]魏喜庆,顾龙飞,李瑞康,等.基于Singer模型的高超声速飞行器轨迹跟踪与预测[J].航天控制,2017, 35(4): 62-66, 72.
[7]张燕,柳超,李云鹏.基于改进Singer模型的机动目标跟踪方法[J].火控雷达技术,2015, 44(3): 37-40, 50.
[8] Geng Y R,Wang J L.Adaptive estimation of multiple fadingfactors in Kalman filter for navigation applications[J]. GPS So-lutions, 2008, 12(4): 273-279.
[9] LiX R,Jdkov V P.Survey of maneuvering target tracking.PartI. Dynamic models[J]. IEEE Transactions on Aerospace andElectronic Systems, 2003, 39(4): 1333-1364.
[10] Liu H Z,Tongue B H.Indirect spacecraft trajectory optimiza-tion using modified equinoctial elements[Jl. Journal of Guid-ance, Control,and Dynamics, 2010, 33(2): 619-623.
[11] Jia S Y.Research Institute of Information Fusion Naval Aero-nautical and Astronautical University Yantai China, Zhang Y,et al.Highly maneuvering target tracking using multi-parame-ter fusion singer modeI[J]. Journal of Systems Engineering andElectronics, 2017, 28(5): 841-850.
[12] Wu W, Pan Q,Zhao C H,et al.A probability hypothesis den-sity filter with Singer model for maneuver target tracking[Cy/Proceedings of the 32nd Chinese Control Conference. 26-28July 2013, Xi'an, China.IEEE, 2013: 4778-4782.
[13] Lee Y L,Chen Y W. IMM estimator based on fuzzy weightedinput estimation for tracking a maneuvermg target[Jl. AppliedMathematical Modelling, 2015, 39(19): 5791-5802.
[14] Zhu L H,Cheng X H.High manoeuvre target tracking in co-ordinated turns[J]. lET Radar, Sonar&Navigation, 2015, 9(8):1078-1087.
【通聯编辑:谢媛媛】
作者简介:房晓丽(1985-),女,山东寿光人,讲师,硕士,主要研究方向为信号与信息处理、卫星导航定位等。
