基于余弦相似度-神经网络模型的高铁土建工程造价估算
2020-11-10牛衍亮高立扬段晓晨
牛衍亮,高立扬,段晓晨,赵 丹
(1.石家庄铁道大学 经济管理学院,河北 石家庄 050043;2.中铁二十局集团第四工程有限公司,山东 青岛 266061)
根据我国发展改革委2016年印发的《中长期铁路网规划》,为在最大程度上适应大量旅客的运输和出行需求,从2020到2030年,高速铁路网将大幅度增加影响范围,进一步提高铁路运输的核心作用。高速铁路建设项目投资数额巨大、耗时长、结构复杂、辐射范围广、技术要求高且某些地区的施工难度大,同时也受到时间、地域、市场价格、施工设计方案等复杂因素的影响。建设项目投资决策实际发生的费用不足工程总造价的5%,但其对整个项目的总造价有15%~95%的影响[1],因此决策阶段的投资估算需要精益求精,这对整个高速铁路建设项目的资金配置具有重要意义。另外,工程总承包项目投标额也需要精准的造价估算。
目前,造价工作者大多沿用传统的、简单的线性模型(单位生产能力估算法、生产能力指数估算法、比例估算法、朗格系数法、资金周转率法等)进行造价估算,从而导致工程造价估算精度普遍较低,越来越不满足投资决策及工程总承包项目投标额确定的要求。大量高铁项目出现大幅的“三超”现象,使高铁业界与学界越来越关注投资估算的准确性及其方法问题[2,3]。
BP神经网络是学界研究的热点,国内外均有学者针对其算法和应用进行研究。Anastasiadis等[4]对传统的BP神经网络进行了网络结构的改进。周丽萍、胡振锋[5]主要针对建筑工程项目应用BP神经网络计算出项目的造价,经过误差测算,结果满足精度要求,论证了方法的可行性。段晓晨等[6,7]立足于研究工程项目修建产生的环境成本,提出一种适用性更强的算法,即将BP神经网络同传统的线性算法结合,构建了非线性环境成本预测模型。
综上,本文将显著性成本理论与基于余弦相似度-神经网络模型的造价估算方法相结合,研究高铁土建工程非线性投资估算。首先运用显著性成本理论、灰色关联分析、专家访谈,识别影响高铁土建工程造价的显著性成本因子,构建高铁土建工程造价基础数据库。然后运用余弦相似度方法在构建的造价基础数据库中选取与拟建项目相类似的案例集。然后使用BP神经网络确定显著性成本因子与造价的非线性关系,实现基于余弦相似度-神经网络模型的高铁拟建工程项目的土建工程造价估算[1]。
1 基于显著性成本理论的高铁土建工程造价影响因子识别
1.1 显著性成本理论
Saket[8],Asif[9],Zakieh[10]等人在研究工程项目的造价构成时发现:18%的工程子目成本占据项目总成本的81%,也就是说大约有20%的项目子目成本构成了80%的总造价(二八原则)。同时,这些研究显示拟建项目的显著性成本因子和已完工程的显著性成本因子有很大的相似性。
通过铁路项目调研、文献资料阅读、问卷调查、网络新闻报道等方式获得数据信息;结合已完工程在其决策阶段、设计阶段、施工阶段、竣工结算阶段的基础数据信息,分析得到高铁土建工程造价影响因素集(工程特征)。按照式(1)在显著性成本理论的基础上,针对已经建设完毕的高铁土建工程的工程特征分类汇总后,选取影响其造价的显著性成本因子。
(1)
式中:C为高铁项目土建工程总造价;N为高铁项目土建工程的工程特征个数;T为高铁项目土建工程特征平均造价。
在已完工项目分部分项中的139个工程特征中,有34个工程特征(约占全部工程特征的20%)的造价影响高于平均值;并且对各个已完工程的34个工程特征的造价求和后,发现其占据整个土建工程造价的80%左右,因此将其确定为影响造价的显著性成本因子,并且通过灰色关联度和专家访谈方法分析确认后,最终得出影响高铁土建工程造价的显著性成本因子,如表1所示。由于文章篇幅限制,通过灰色关联分析、专家访谈方法进行分析和验证的具体过程未列出,如有需要,可向作者索取。

表1 高铁土建工程造价显著性成本因子及文献识别
1.2 高铁土建工程造价估算信息基础数据库构建
基于课题组参与的高铁项目数据,以及专项业界调研收集的项目报价单及造价相关资料,并与期刊、《铁路年鉴》等数据相对照,建立了包含含40个高铁项目案例的数据库(关于各高铁项目34个指标的具体信息以及指标量化方法,由于篇幅所限,如有需要,可向作者索取)。同时,由于各项目建设时间不同,需要对数据进行时间调整。本文在对拟建项目进行造价估算时,将已完工项目的最终造价数据统一折算到2018年底。以案例高铁项目竣工年为研究基年,将其造价通过历年的通货膨胀系数调整到2018年。由于案例库项目从2008年开始,因此搜集2008~2018年的通货膨胀系数,按照式(2)计算,将其设为α。
α=(1+a1)(1+a2)(1+a3)…(1+an)
(2)
式中:a1~an为统计的从2008~2018年每年的通货膨胀系数。
除此之外,还需要对不同地区的项目进行调整,根据当地的造价指数可以将不同地区的项目调整至基准地区。但由于我国高铁项目的分区域造价指数还没有公开的信息,所以此项工作有待于后续完善。
综上,得到已完工高铁项目造价指标量化值示于表2。
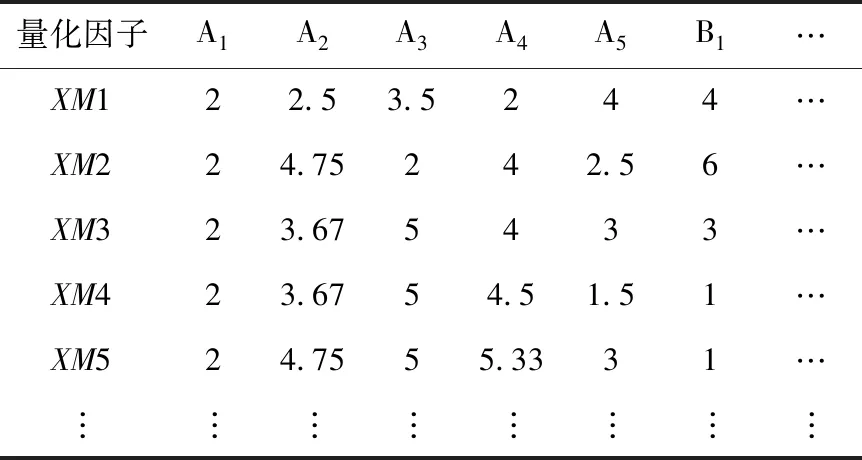
表2 已完工高铁建设项目显著性因子量化值
2 基于余弦相似度-BP神经网络的高铁土建工程造价估算模型构建
2.1 余弦相似度选取已完工类似工程
余弦相似度是一种变量间的相似度测量方法,即计算各个个体间的相似程度。得出的数值越小,说明个体间相似度越小;反之说明研究的个体间的相似度越大[36]。余弦相似度具有很强的稳定性和交叉性,且由于原理基于扎实的基础数学理论,得到了众多领域的研究与应用。经过前人大量的实验得出此方法在分析特征的相似度上有较高的准确性,同时其运算过程具有较为简便的特点。在比较了多种分析已完工类似工程和拟建工程相似度的方法后,文章选取余弦相似性分析方法进行项目间相似度的判别。
余弦相似度的测量是运用两个向量的内积空间夹角α的余弦值来度量两个个体间的相似性。两个向量m与n之间的余弦相似度按照式(3)计算。
(3)
在搜索个体的显著性成本因子的过程中,研究对象的特征由一个有权值的特征向量表示,任意两个样本A,B的余弦相似度按照式(4)计算。
(4)
式中:n为样本空间项目总数;Xi,Yi表示第i个显著性成本因子在项目X,Y中分别对应的数量。余弦相似度方法界定的个体间相似性范围为(-1,1)。其中,-1表示两个向量指向的方向呈现180°的角,表示完全没有相似性;1表示两个向量夹角是0°,表示相似性最高;0通常表示两个向量之间是相互独立的,表示两个个体之间没有相似的关系。
根据研究个体的实际情况来设定余弦相似度阈值,从而可以确定变量之间的相似程度[37],其阈值范围示于表3。

表3 余弦相似度对应变量相关性
因此,通过整合已完类似工程特征,对其进行量化处理,将每个项目的工程特征当作一个矩阵。将拟建工程项目工程特征进行量化处理后与已完工项目两两比较,通过相似度公式计算得来二者的相关性。根据相似度的划分可以得到造价预测模型的基础数据。
2.2 BP神经网络造价预测
BP(BackPropagation)神经网络是对计算出的误差进行一种反向训练传播并纠正的神经网络的简称。它由输入层、隐含层和输出层组成,类似于人脑的传播反馈系统。这些神经元如同人的神经细胞一样是彼此之间互相关联的。BP神经网络结构的输入层、隐含层、输出层分别有n个、p个、q个神经元[38,39]。针对传统的标准3层BP神经网络,文章通过MATLABR2016a来实现预测。
(1)输入、输出神经元的确定
为构建高铁土建工程造价非线性估算模型,BP神经网络中的输入层为选取的影响高铁土建造价显著性成本因子,然后通过隐含层对输入的数值通过计算处理传输到输出层,最后输出层针对计算出的结果自动与期望的数值进行分析对比。如果输入值和输出值相差较大,则开始进行误差的反向传播,直到达到理想值为止。
(2)隐含层神经元数的确定
设置适当的隐含层个数来达到预测的精度要求,实现降低误差的目的。在许多具体的实验测算过程中,确定隐含层个数的方法就是根据柯尔莫哥洛夫定理,因此文章也参照此方法将隐含层神经元数量计为2r+1(其中,r表示输入层数据的个数)。
(3)初始权值确定
对于初始值,在BP神经网络运算系统的过程中通过(-1,1)之间的随机数实现。
(4)节点函数的确定
由于Sigmoid函数对任何数据的输入都可以转化为(0,1)之间的数,故文章选取其作为节点输出函数。
3 基于余弦相似度-神经网络高铁土建工程造价估算模型应用
3.1 案例概况
新建贵阳至南宁铁路位于贵州省东南部和广西壮族自治区西北部,本标段的设计行车速度为350km/h,2018年1月开工,计划2023年12月竣工。正线长度21.353km。该标段位于贵州贵定、都匀境内,贵定地区地貌类型是高原。都匀地区的北部山地分布广;中南部河流众多,有大面积的盆地;该地区地貌有较广范围的喀斯特地貌,有大面积的侵蚀现象;地形类型多样,山地、丘陵、盆地、河谷相间分布。表层的土质为粉质黏土,不良地质灾害主要来自于顺岩、危岩落石。
3.2 基于余弦相似度计算拟建项目相似度
依据所建立的高速铁路建设项目工程特征可以对贵阳至南宁高铁贵州段GNZQ-2标段进行全面系统的描述,然后量化,运用MATLABR2016a运算结果,拟建项目与已完工项目的相似度示于表4。
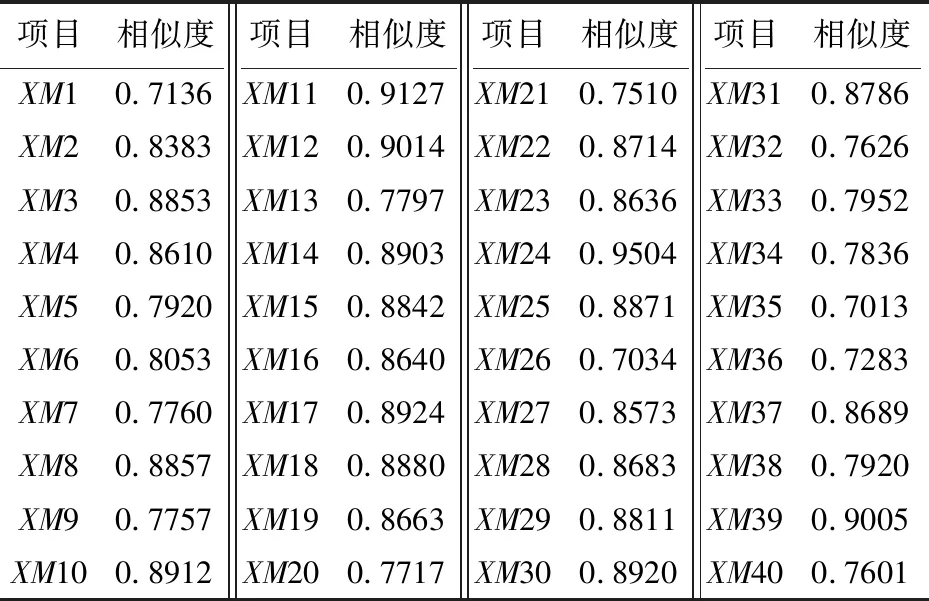
表4 余弦相似度结果
3.3 基于余弦相似度-BP神经网络高铁土建工程造价估算
文章选取与拟建项目相似度在0.8以上的项目作为类似工程样本进行测算,即有25个类似案例。根据输入-输出映射复杂程度,将其中23个项目作为训练样本,2个项目作为测试样本,用MATLABR2016a中提供的BP网络函数构建模型。
构建BP网络主要过程如下:
(1)按照式(5)将输入向量I1~I34输出向量数据标准化
(5)
式中:Xij为原向量数据;X′ij为标准化后数据,用X′ij代替相应Xij,得出BP神经网络的基础数据。
(2)构建BP网络
输入参数为34个输入单元,69个隐层单元,1个输出单元,其余为默认值。
(3)训练BP网络
将第1~23个工程数据作为训练样本,最大迭代次数200次,容许误差10-18,运算过程和误差曲线如图1,2所示。
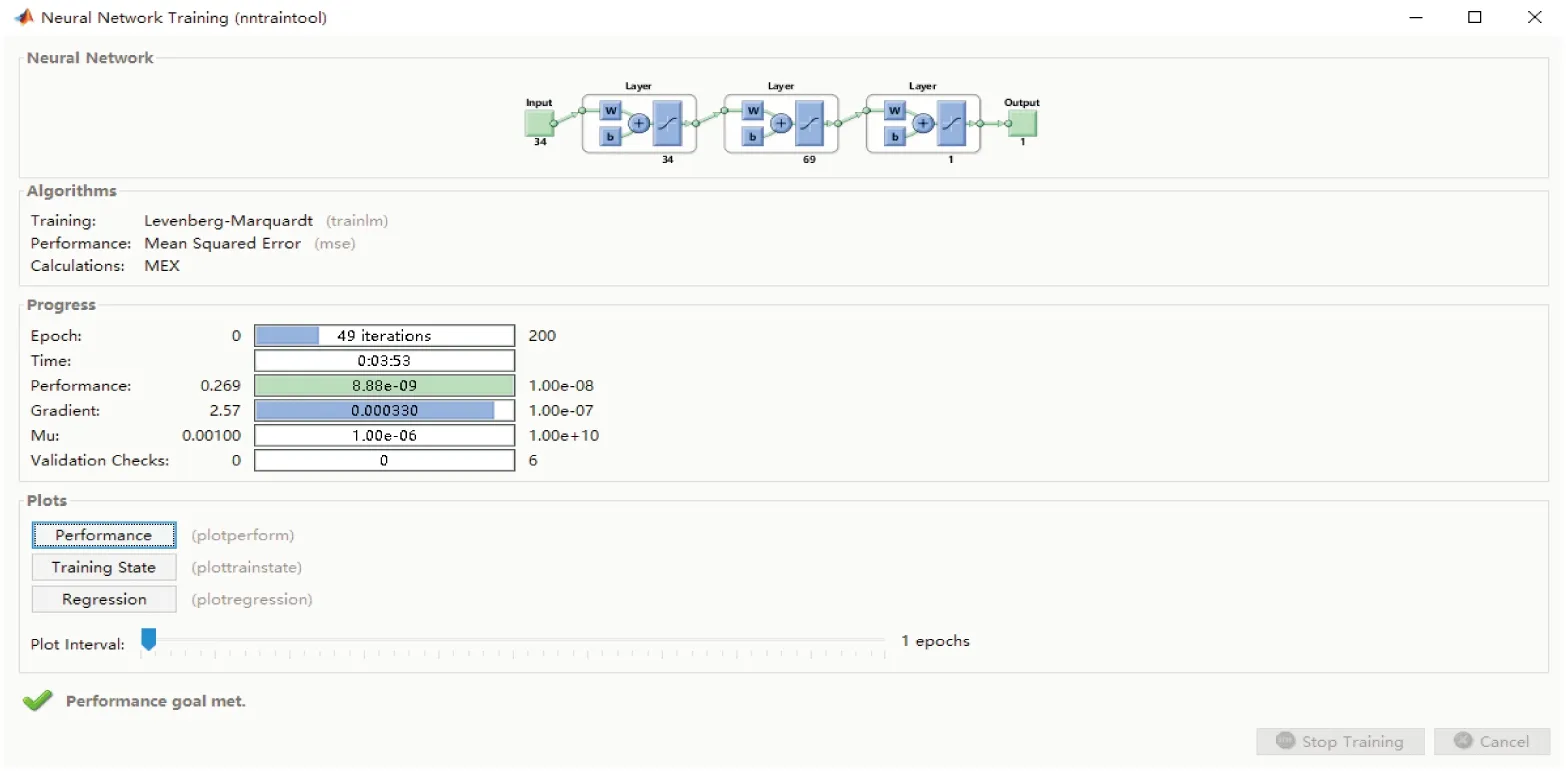
图1 训练过程

图2 误差曲线
由于神经网络预测模型初始化的权值和阈值是随机的,因此导致模型输出结果不是一个定值。在这种情况下,参考前人处理经验,对模型进行多次运算来消除随机性带来的误差,文章进行了10次运行,结果如表5所示。
根据多次运行结果运用不同的方法测算后,在对输出结果采用均值法进行处理所得到的与实际值的误差都在5%以内(其中,拟建项目造价实际值是指中标单位的单位投标报价),经过学界和业界论证后此误差范围符合项目的误差要求且精度较高。故采用训练后的模型对贵阳至南宁高铁贵州段GNZQ-2标段单位造价的预测合理可行。
通过分析表5的数据可以发现:预测的组数据中,预测结果与实际值的绝对误差均小于500万元。预测样本的相对误差最大为3.74%,相对误差最小的为1.31%,都在±5%以内。因此,采用神经网络构建的高铁土建工程造价预测模型来进行投资估算的预测效果很好,相对误差较小。
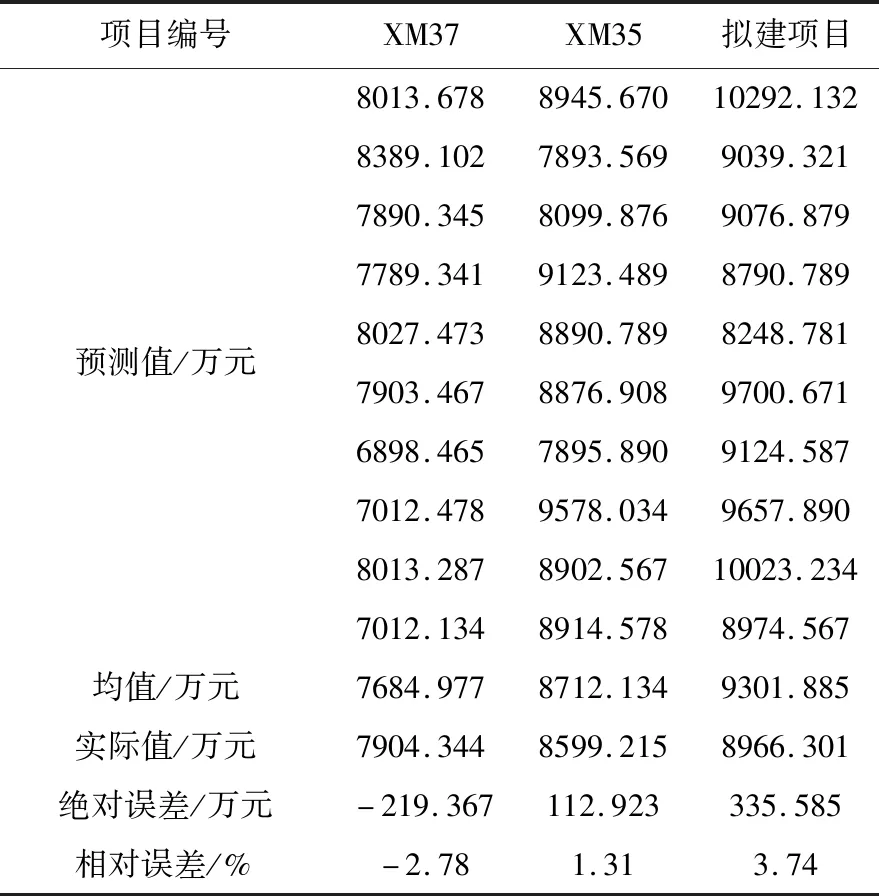
表5 贵阳至南宁高铁贵州段GNZQ-2标段建设成本分析
4 结 论
本研究的主要工作包括:(1)通过大量文献识别高铁造价影响因素,并基于显著性成本理论通过对因子进行定量分析最终确定显著性成本因子;(2)运用余弦相似度方法选取案例库中的已完工类似工程,确定相似度在0.8以上的已完工工程为造价预测的基础数据库,具有较强的可操作性和科学性;(3)借助MATLAB R2016a 软件实现BP神经网络造价估算,虽然BP神经网络是一种“黑箱”训练,拟建项目的造价和已完工类似工程的造价相似度具有模糊性,但是其具有反向学习、较高的容错性能,这也达到了快速处理数据的要求,通过多次试验,求得预测造价值的平均值可以降低随机性,并达到精度要求,提高了高铁土建工程造价估算的准确度。
