基于卷积神经网络的合成双射流控制机翼分离流场识别与参数优化

赵志杰, 罗振兵, 邓 雄

(国防科技大学 空天科学学院, 长沙 410073)

0 引 言

自Glezer[1]首次发明合成射流激励器(SJA)并将其应用于流动控制研究中以来，合成射流技术便受到了广泛的关注。合成射流技术通过在流场中不稳定点处施加周期性小扰动，从而实现对全流场流动状态的控制，具有“四两拨千斤”的效果[2-3]，在分离流动控制[4-8]、推力矢量控制[9-10]、增强掺混[11]、激波控制[12-14]、强化换热[15-17]、航行器姿态控制[18]等领域展现出广阔的应用前景。SJA作为合成射流的发生装置，其结构影响着合成射流的性能参数。传统的SJA具有结构紧凑、易于实现电参数控制等优点，但由于其膜片的一端直接暴露在外部环境中，有至少一半的振动声能未得到充分利用，当膜片两端压差过大时，甚至会导致激励器压载失效。基于此，国防科技大学罗振兵[19]对SJA进行了结构优化设计，发明了合成双射流激励器(DSJA)，其结构如图1所示，该激励器不仅解决了激励器能量利用率低、压载失效的问题，同时还具有“穿透”能力强、下游流动稳定、速度更高等优点。

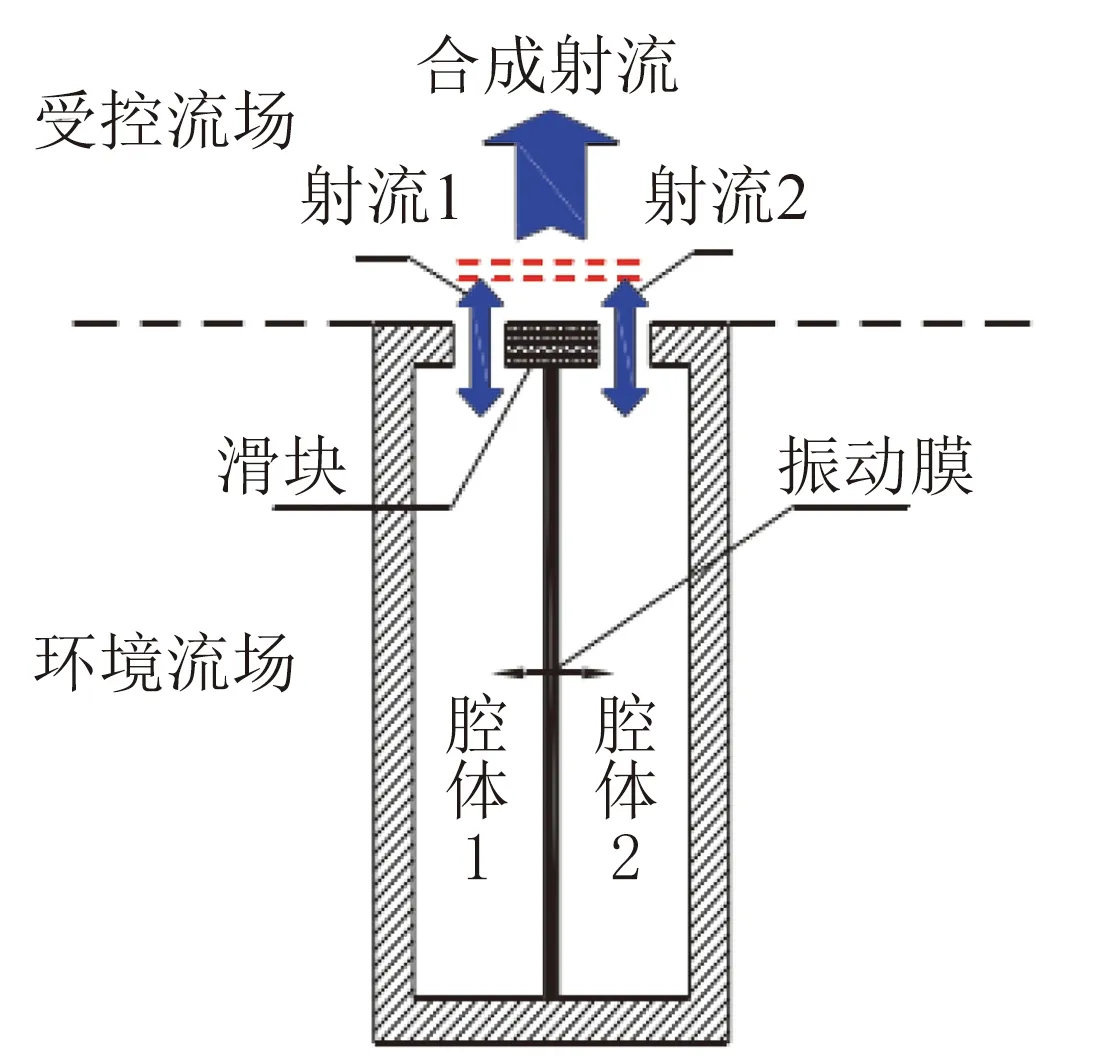
图1 合成双射流激励器结构示意图Fig.1 The structure diagram of DSJA

在飞行器飞行中，随着气流迎角的增大，吸力面会出现较大的逆压梯度。当近壁面气流自身能量无法克服逆压梯度及表面黏性时，便会导致吸力面发生附面层分离，使飞机气动性能变差。为抑制吸力面大范围流动分离，防止失速现象的发生，国内外诸多学者将合成射流技术作为分离流控制手段，并对其机理、最佳控制参数进行了探讨。Glezer等[20-21]认为在小迎角下，合成射流在出口处形成了局部回流区以改变局部流线，在光滑翼型表面形成了“虚拟气动外形”，改变了边界层厚度和表面压力分布，从而改善了气动性能。张攀峰、王晋军、刘峰等[22-25]通过数值模拟得出合成射流在射流偏角为30°，射流位置在分离点之前或在分离点附近偏后的位置时控制效果较好，且控制效果随射流动量系数的增加而增加。王林、李玉杰[26-27]等分别通过数值模拟与试验证明，合成双射流(DSJ)相比与传统的合成射流具有更好的控制效果，激励器工作频率为流场特征频率的1和2倍时，对翼型气动特性的改善效果最好，同时控制效果会随动量系数的增加而增大，合成双射流两出口在分离点之前(不能太靠前)或在分离点之间时有较强的控制效果。上述研究虽然获得了合成射流/合成双射流对分离流的控制规律，但缺少用智能化的方法对大量的实验数据进行进一步的挖掘。

本文在上述研究的基础上，以NACA0015为基础翼型，通过数值模拟探讨机翼失速后DSJ频率、动量对流场控制效果的影响及机理，建立控制参数向量与升、阻力系数的RBF神经网络代理模型，通过改进的粒子群算法(PSO)得出激励器最佳的控制参数，并搭建Inception-V3卷积神经网络，以迁移学习的方式实现对平均流场控制参数的识别，为DSJA进一步的实际工程应用提供有意义的参考。

1 计算方法及验证

仿真中气流Ma<0.3，气体视为不可压缩流体。采用的控制方程为二维不可压非定常雷诺平均Navier-Stokes方程组，利用Fluent软件进行不可压显式求解。因为流动中伴随着流动分离、涡流等流动现象，所以湍流模型选用SSTk-w模型。时间上采用一阶显式格式，空间离散采用二阶迎风格式，压力修正采用压力隐式算子分裂PISO算法。

计算所采用的翼型为NACA0015翼型，其弦长c为375 mm，自由来流速度为U∞为27.3 m/s，基于弦长c的Re为7×105。DSJA的位置布置在距离前缘x/c=10%的位置，射流出口宽度相对翼型弦长为h/c=0.53%，两射流出口间距为1.4%c，设定射流偏角(射流方向与弦线的夹角)为30°，具体位置如图2(a)所示。为减小远场边界对计算结果的影响，设置外流计算域半圆段半径为15c，翼型尾缘距计算域末端距离为25c。计算网格为基于多块网格对接技术的结构化C型网格，以保证近壁面网格的正交性，其计算域及网格如图2(b)所示。计算网格在翼型表面及射流出口处进行了加密，射流出口处设置网格点数为6，两射流间距处设置网格点数为15，保证物面的第一层网格高度y+<1。数值模拟中共进行240个周期的非定常计算，其中前80个周期用于未施加控制的基准状态计算，后160个周期用于施加射流控制的计算，气动力系数取最后10个周期的平均值。

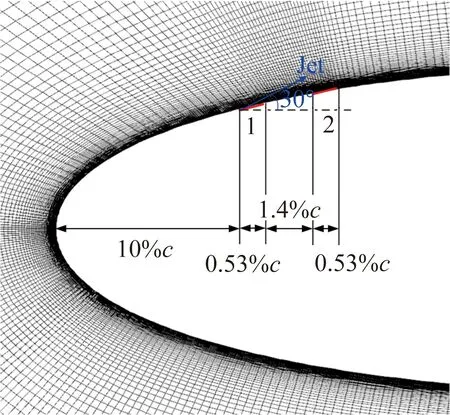
(a) 射流位置及网格分布图

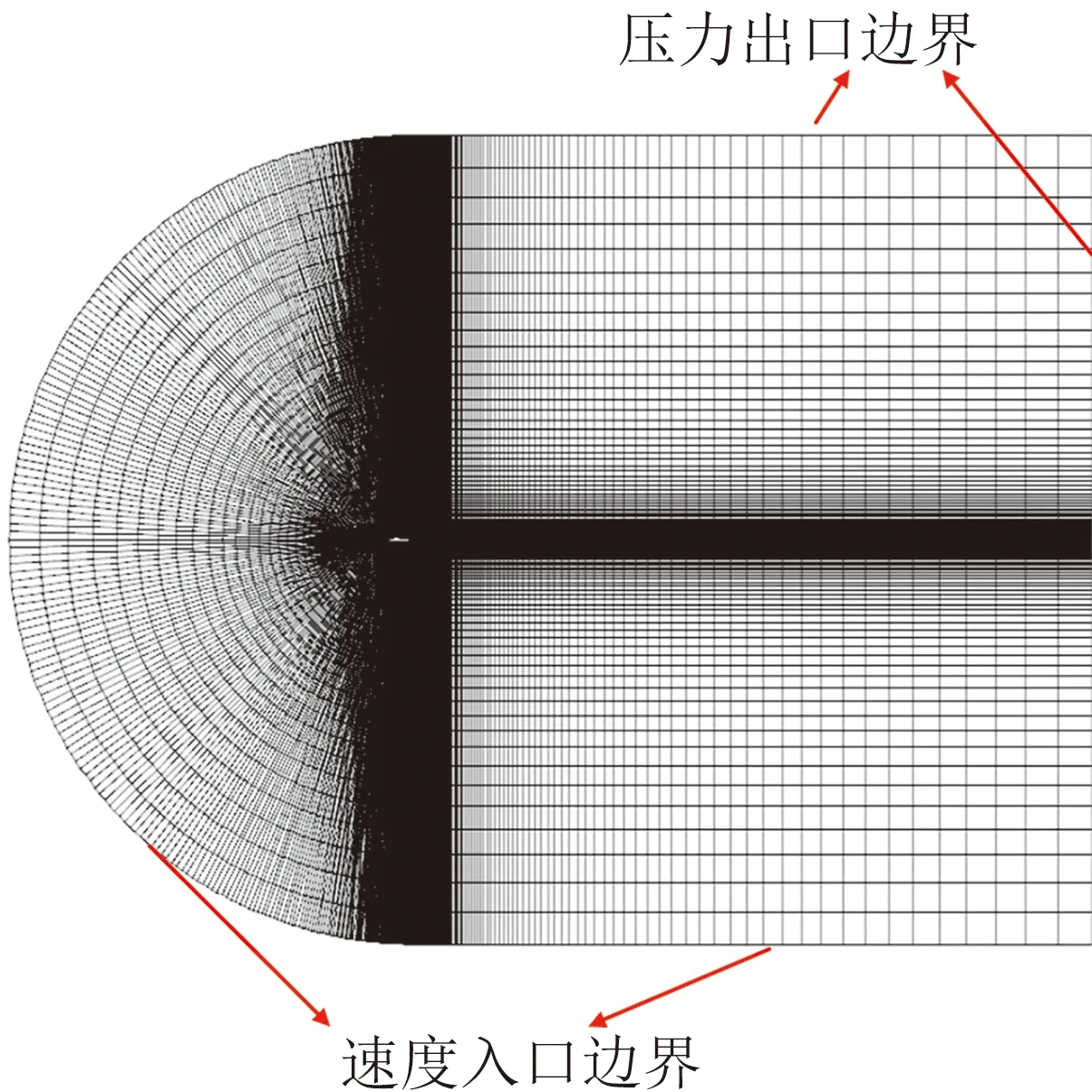
(b) 整体计算域及网格示意图

在计算时分别采取了数量为100 221、163 221、201 131的网格进行计算，在没有DSJ控制下，迎角为8°时的升、阻力系数分别如表1所示。在网格数大于163221时，升、阻力系数已经趋于稳定，故选择计算总网格数为163 221。分别采用S-A模型与SSTk-w模型进行计算，得到的升、阻力系数与实验结果[28]对比如图3所示，可发现在小迎角下，两种模型所计算的升阻力系数误差均较小，大迎角下，RANS模型的计算误差较大，SSTk-w模型的计算误差相对较小，且其在失速后的变化趋势与实验较为一致，又本文主要关注失速后流场特性，故采用SSTk-w模型作为本研究的计算湍流模型。

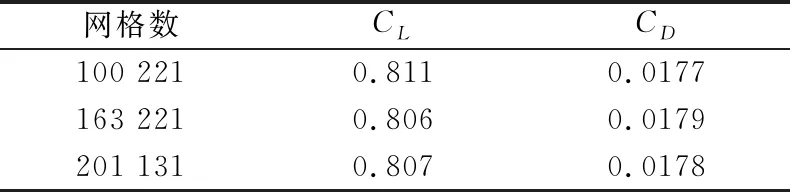
表1 不同网格下，升、阻力系数对比Table 1 Comparison of CLand CDin different grids

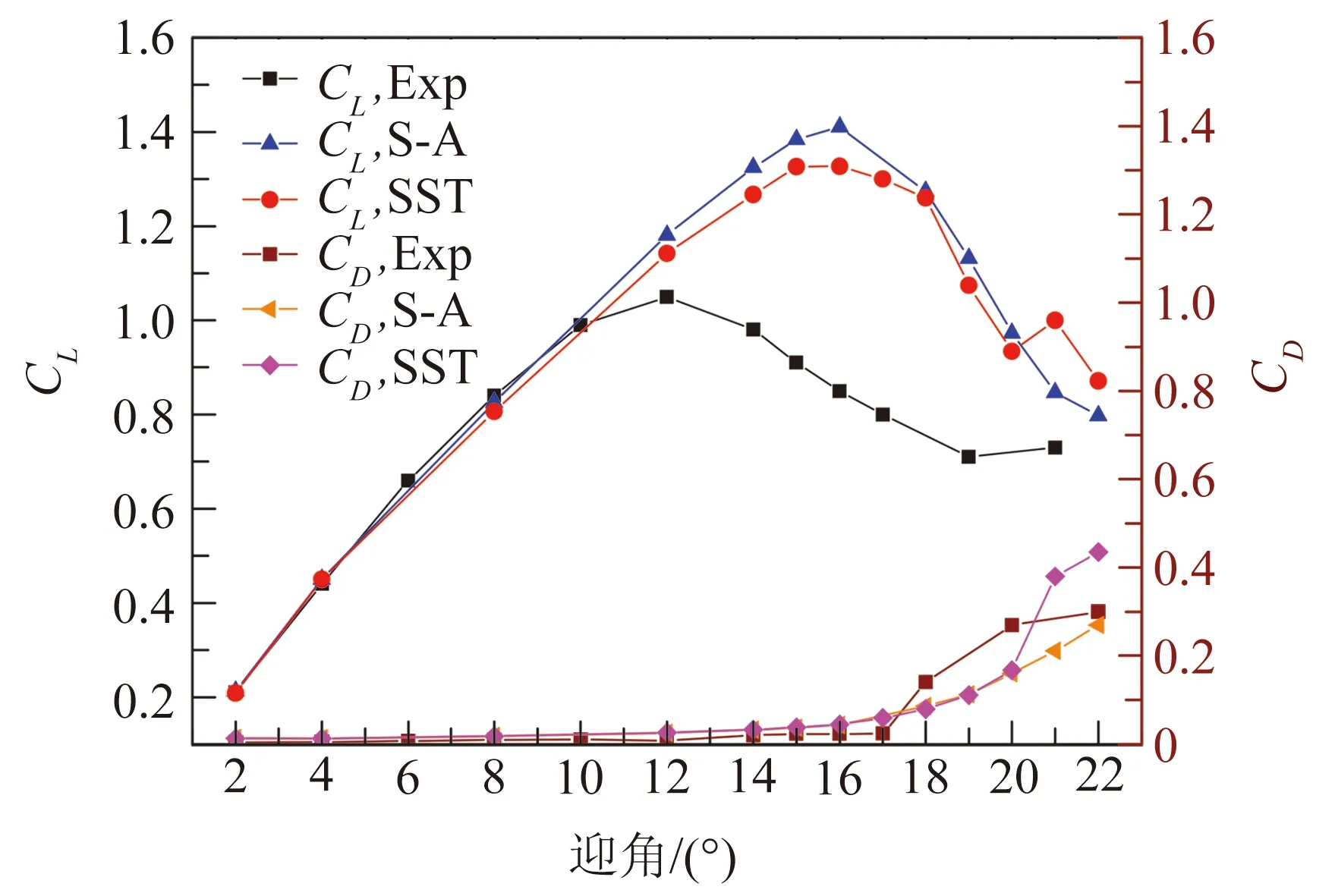
图3 数值模拟与实验数据[28]对比分析Fig.3 Comparison between numerical simulations and experimental data[28]

定义计算域左、下边界为速度入口边界，上、右边界为压力出口边界，翼型表面设置为无滑移绝热壁面边界。为简化DSJ的工作过程，直接采用在翼型表面设置速度入口的方式。利用UDF加载射流速度入口边界条件为：

u1=Umaxsin (2πft+φ0)

(1)

u2=Umaxsin (2πft+π+φ0)

(2)

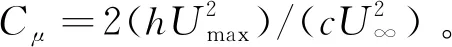
2 计算结果与分析

2.1 控制效果与机理

以迎角20°时，翼型在未施加控制及施加控制(F+=2,Cμ=0.0424)后的平均流场为例，探究DSJ的控制机理，其速度场及表面压力分布对比如图4所示，相关气动参数对比(升力系数CL、阻力系数CD、气流分离点dp、升阻比)如表2所示。

表2 施加控制与未施加控制时的气动参数对比Table 2 Comparison of aerodynamic performances between having control and no control

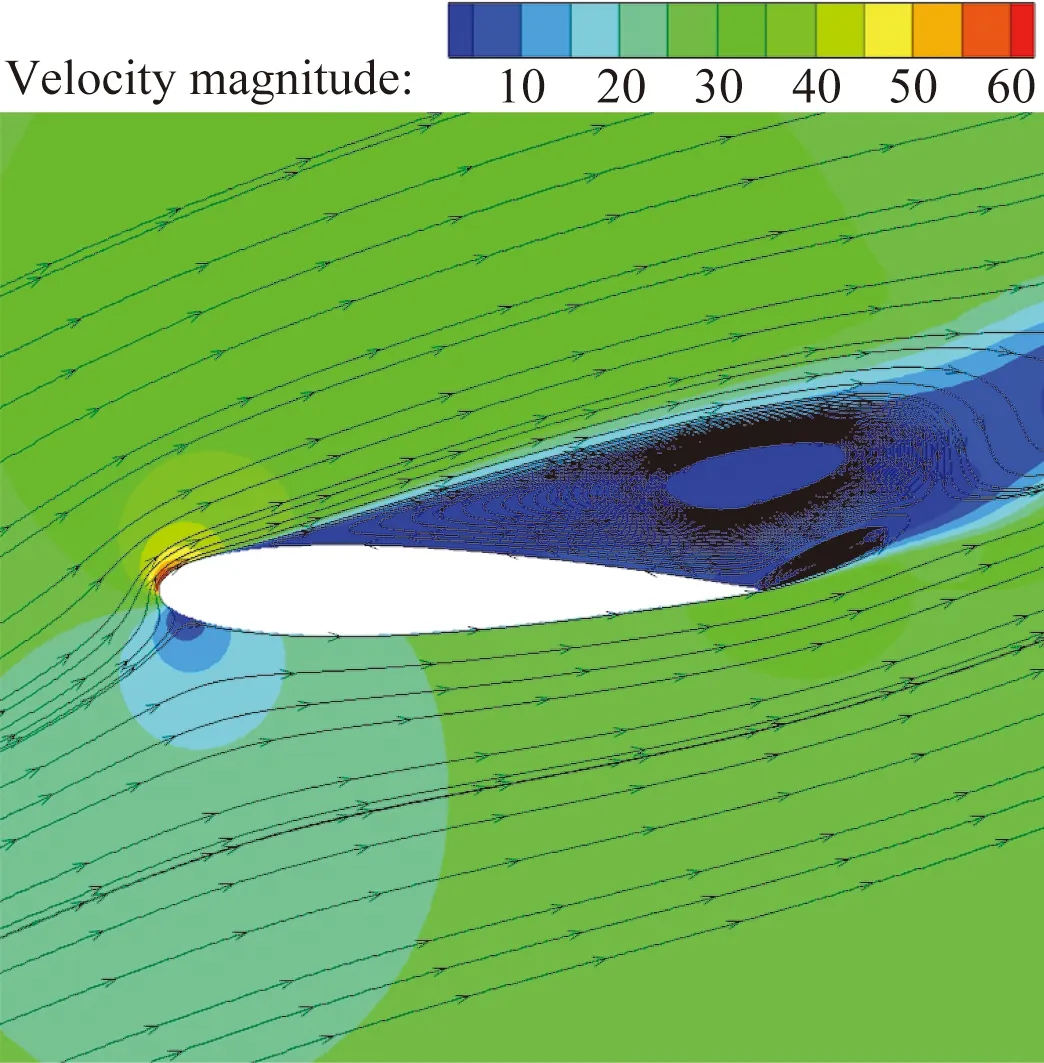
(a) 无控

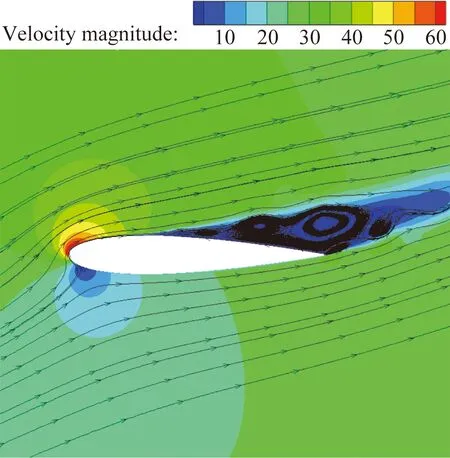
(b) 施加控制

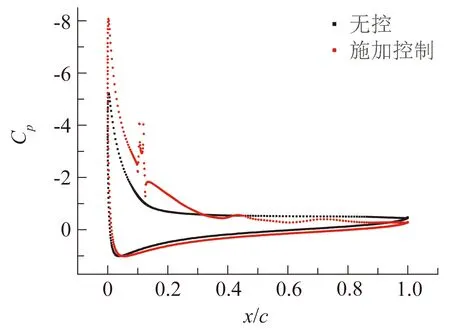
(c) 施加控制前后表面压力系数分布对比图

在未施加控制时，吸力面气流在大逆压梯度的作用下于12.16%c处发生严重分离，并在下游形成较大的分离区，由于此时分离区较大，前缘吸力峰值较小，故产生的升力也较小，此外，吸力面的后缘上因为分离区的存在而产生大面积低压区，且此时迎角较大，故产生的压差阻力较大。可见，削弱或抑制大面积分离区是增升减阻的关键。在施加DSJ控制后，前缘吸力峰值大幅度提升，在DSJ出口处分别形成两个局部极大吸力峰，在两出口之间出现局部极小吸力峰，该极小吸力峰的出现是由于2出口喷出射流的法向阻塞所用所致；在压力恢复区内，吸力面压力系数呈现出小幅低频波动的特点，这是DSJ与壁面剪切所形成的涡向下游迁移并逐步耗散的结果；整体上看，吸力面(0～0.3c区域)压力系数(绝对值)整体提升，吸力面(0.3c～后缘区域)压力系数(绝对值)整体下降，这是由于分离区减小，对外流的压缩减小，分离区外流速度相对较小，静压相对较大，故翼型表面压力系数相对较大；压力面压力系数(绝对值)略有上升，这相当于在光滑翼型表面形成了一虚拟形面。由图4(a、b)可看出，施加控制后，气流分离得到很大抑制，气流分离点由12.16%c延后至38.67%c，升力系数、阻力系数均提高，升阻比提高至15.417，大约是未施加控制时的3倍，可见，DSJ可以实现对分离区的有效控制。

DSJ对分离区的控制机理包括动量注入效应、涡掺混效应、抽吸效应。在射流的吹阶段，高能射流注入到能量较低的附面层中，使附面层内流体能量增加，抵抗逆压梯度的能力增大，从而抑制附面层分离，即动量注入效应；射流出口处形成的涡对可加强边界层底部低速流体与主流中高能流体的掺混，增大边界层内流体的能量，使其抵抗逆压梯度的能力增加，延缓流动分离，即涡掺混效应；在射流的吸阶段，附面层的低能流体被吸除，使边界层厚度降低，抑制流动分离，即抽吸效应。

2.2 控制参数对DSJ控制效果的影响

图5给出了迎角为16°、17°、18°、19°、20°、21°、22°、24°时，射流无量纲频率F+与动量系数Cμ对流动控制效果的影响图。在迎角为16°～21°时，动量系数越大，增升减阻的效果越明显；F+在0.5～4范围内均有较好的控制效果。在迎角为22°时，此时气流在吸力面发生大面积分离，从图中仍可看出动量系数起较大影响作用，动量系数越大，增升减阻效果越明显，值得注意的是，F+=0.5、Cμ=0.0424时，阻力系数较未控制时反而增加，可见F+=0.5并非在该迎角下的最佳驱动频率。在迎角为24°时，分离区面积进一步扩大，在小动量系数下，增升效果不明显，甚至会增大阻力；在提高动量系数后，增升效果有明显提升，但当F+=0.5～1时，阻力增大，气动性能恶化。可见，在控制大面积流动分离时，应增大射流动量，F+应控制在3～4之间，以达到良好的控制效果。

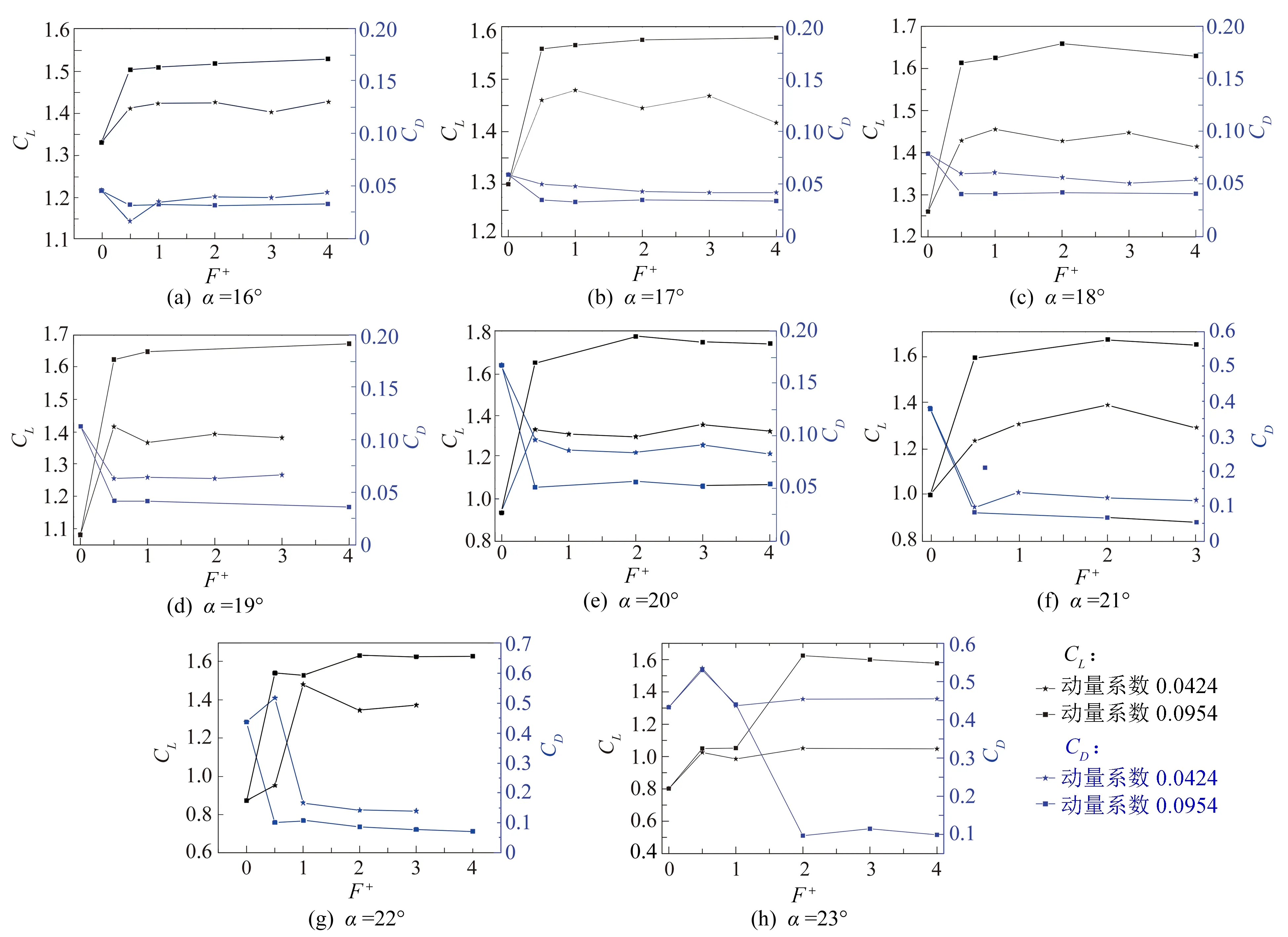
图5 不同迎角下控制效果对比图Fig.5 Comparison of control effects at different angles of attack

3 控制参数向量优化

利用RBF神经网络构建控制向量(迎角α、射流无量纲频率F+、动量系数Cμ)与升、阻力系数(CL、CD)之间的代理模型，并采用粒子群算法(PSO)搜索在一定约束下的最大升力系数、最小阻力系数及其所对应的控制参数向量。

3.1 RBF神经网络代理模型的构建

RBF神经网络模型的基本思想是用RBF作为隐单元的“基”构成隐含层空间，将输入向量直接映射到隐空间，而从隐含层空间到输出空间的映射是线性的。总体上看，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言是线性的，网络的权可直接由线性方程解出，这样的网络结构不仅加快了学习速度，而且避免了局部极小的问题。

在将数据带入RBF神经网络进行学习之前，对α、F+、Cμ进行最大最小归一化处理，将数据范围放缩至[0,1]区间。由于数据库中数据较少，故随机选取10组数据作为测试集，其余皆作为训练集参与训练。选取高斯函数作为激活函数，采用自组织选取中心法对RBF网络进行训练，首先采用基于K-means聚类求解隐含层基函数的中心，然后采用最小二乘法直接求解隐含层与输出层之间的权值。按以上学习过程，分别构建控制向量与升、阻力系数之间的代理模型，各个模型之间的测试误差如图6所示，可见，测试误差最大不超过17%(升力系数最大误差<1%，阻力系数最大误差<17%)，符合本研究所要求的精度，RBF神经网络可以很好的拟合控制向量与升、阻力系数之间的因果关系。

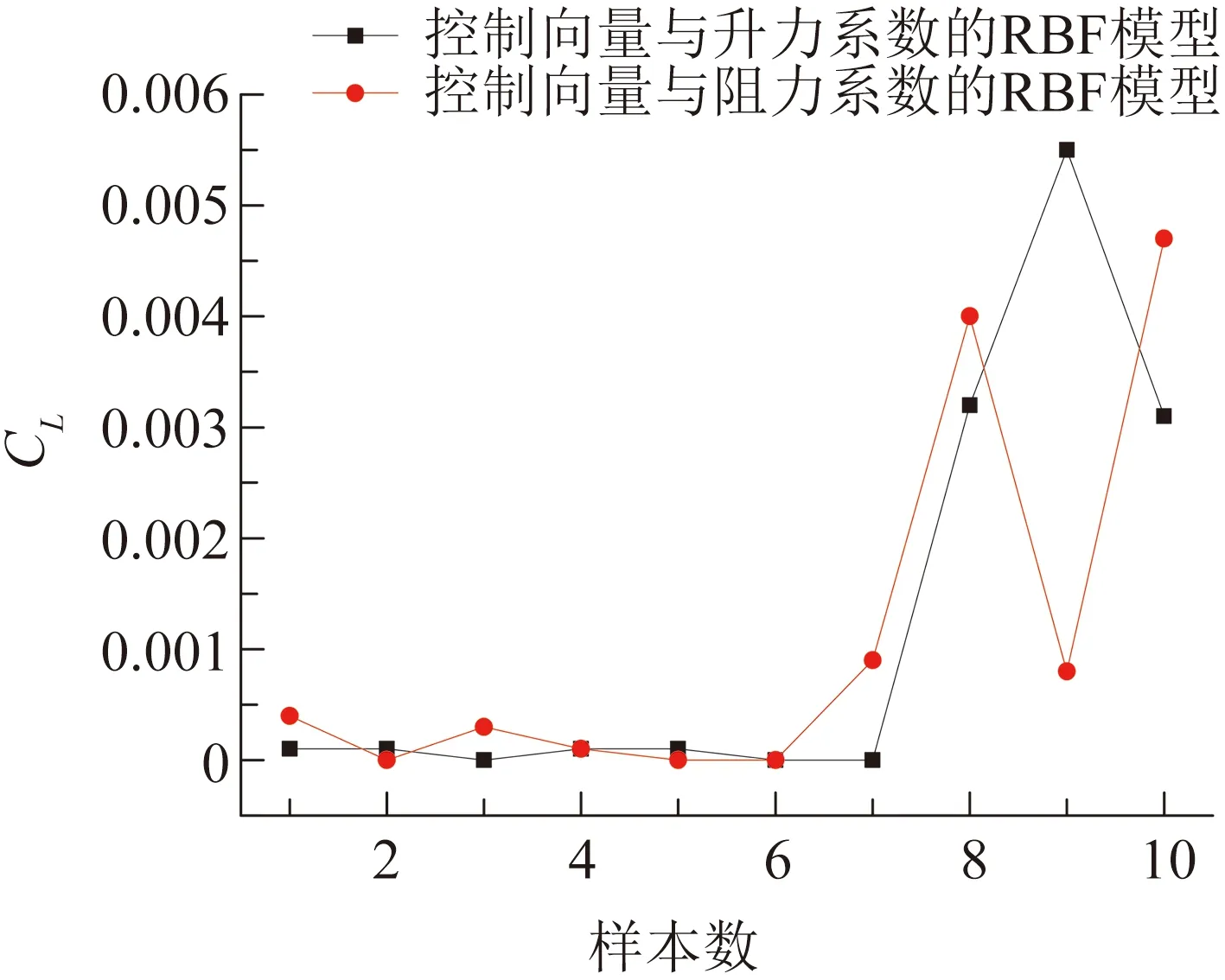
图6 RBF神经网络测试集误差Fig.6 Error of RBF neural network model in test set

3.2 粒子群优化算法(PSO)寻优

PSO在搜索迭代的过程中，粒子位置的更新公式包含有惯性部分、认知部分、社会部分，分别反映了粒子的运动习惯、对自身历史经验的记忆及粒子间协同合作与知识共享的群体历史经验，因此，PSO具有较高的搜索能力。为避免搜索陷入局部最优，采用自适应权重法对PSO进行改进，使惯性权重根据距全局最优点的距离进行调整，非线性动态惯性权重系数更新公式如下：

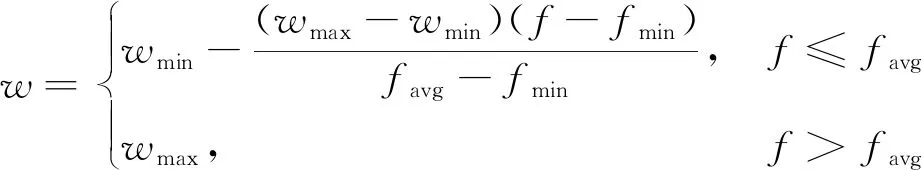
(3)

其中，f为粒子实时目标函数值，favg和fmin分别为当前所有粒子的平均值和最小目标值，wmax和wmin分别为惯性权重最大、最小值。

最优化升力系数的目标函数与约束为：

maxCL

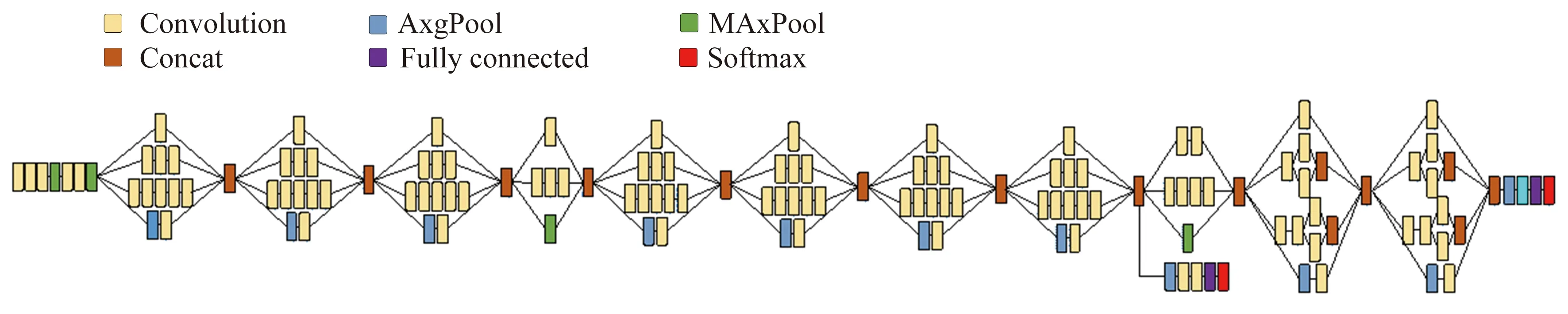
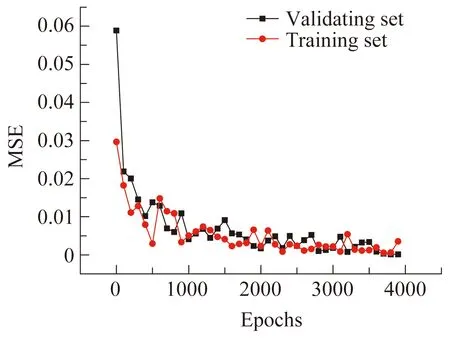
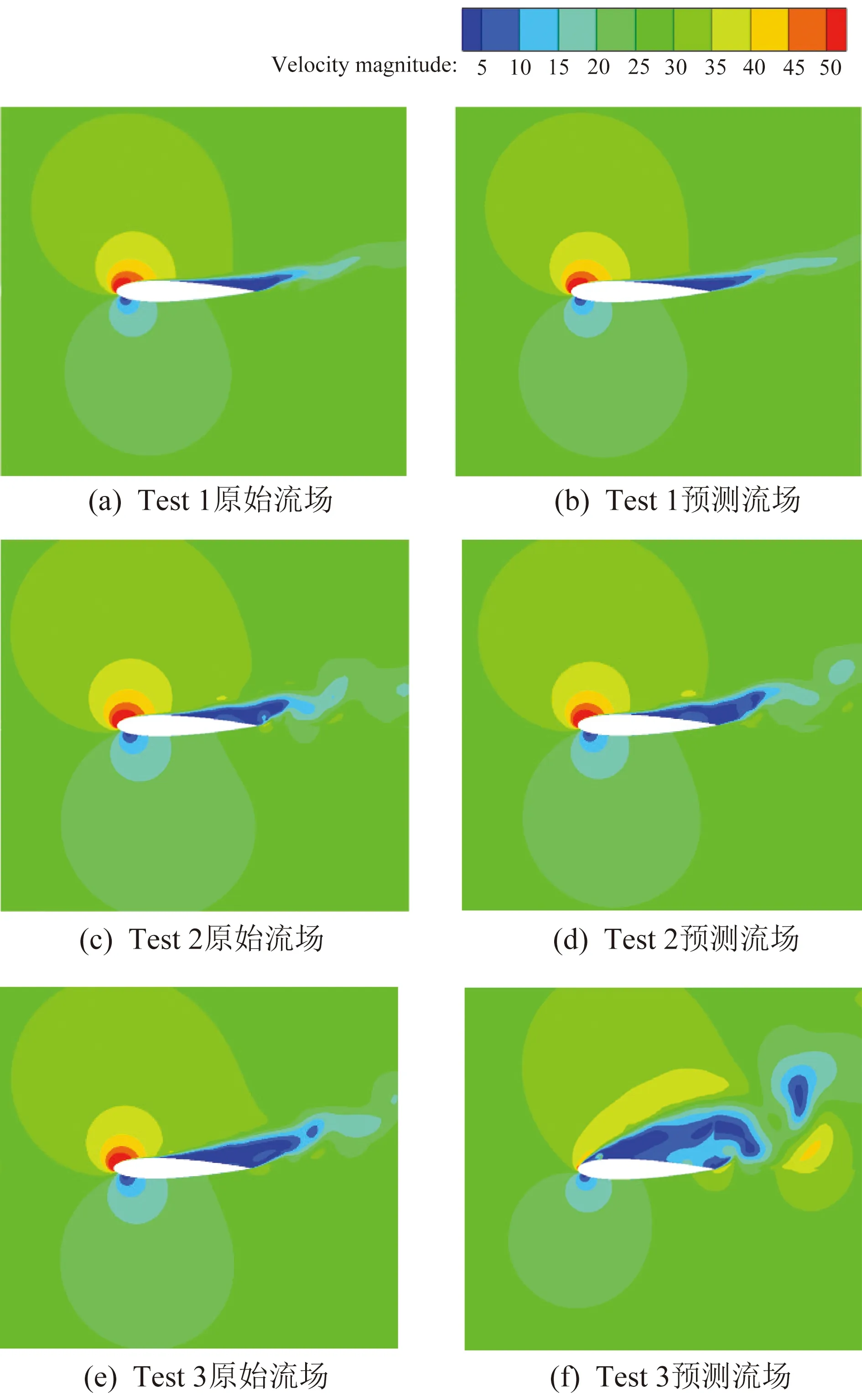
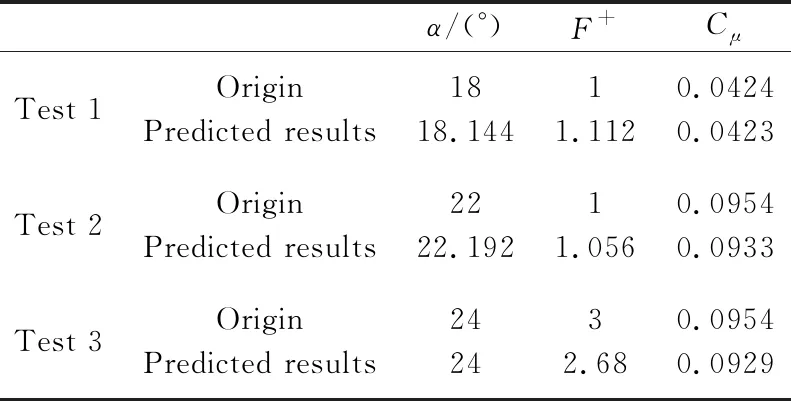
s.t. 16°≤α≤24° , 0

阻力系数的目标函数与约束为：

minCD

s.t. 16°≤α≤24°, 0

学习因子1、学习因子2都设置为2，惯性权重最大、最小值分别为0.8、0.6，种群个体数为200，设定寻找到的最优解在10次迭代中均保持不变为算法终止条件。优化结果如表3所示，可知DSJ在该约束下所能达到的最大升力系数为1.793，最小阻力系数为0.013。

表3 PSO算法优化结果Table 3 Results of PSO

4 基于Inception-V3卷积神经网络的流场识别

升阻力特性无法反映翼型绕流的全局流场特性，故搭建Inception-V3卷积神经网络对全流场速度特性进行特征提取与相应控制参数识别，以实现根据目标流场图像调整激励器参数，使其气动性能达到最优的目的。InceptionNet曾于2014年的ILSVRC比赛中，以top-5错误率(6.67%)略低于VGGNet的优势取得了第一名[29]，Inception-V3模型是对该模型的进一步改进，具有较强的特征提取与图像识别能力。一方面，Inception Moudle通过卷积核的并行连接在卷积神经网络的同一层，提取不同的特征从而降低模型复杂程度; 另一方面，Inception-V3 引入1×1的卷积核，降低了卷积神经网络的参数量和计算量。Inception-V3卷积神经网络模型共有47层，由11个Inception Module组成，其网络结构如图7所示。

图7 Inception-V3卷积神经网络模型[30]Fig.7 Model of Inception-V3 convolutional neural network[30]

为减少训练时间，本文采用迁移学习的方式，保留所有卷积层原始参数，替换掉原模型最后一层全连层，直接将瓶颈层与替换后的全连层(输出层)相连，通过训练Inception-V3卷积神经网络，得出瓶颈层与全连层之间的权重参数值。设定一个batch的数据个数为10，验证集的数据数目为20。设置最大训练步数为4000，初始学习率为0.5，训练目标为最小化控制参数向量(输出)的均方误差(MSE)，采用Adam算法对网络参数进行优化，学习率通过指数衰减法则进行计算，训练集与验证集上的均方误差随训练步数的变化关系如图8所示，可见，在训练步数达到4000次时，模型在训练集与验证集上已具有较高的准确率。

图8 验证集和训练集误差随迭代次数的变化关系Fig.8 Error in validating set and training set with epochs

采用三组算例进行测试，测试结果如表4所示。均方误差分别为：0.0333、0.0399、0.1023，迎角预测误差小于1%，F+预测误差小于11%，Cμ预测误差小于3%，模型预测得出的控制向量与原始图像所对应的控制向量参数相差很小。为了更精确地比较两者之间的差距，分别比较了这两种控制参数下所对应的平均速度场，对比结果如图9所示，可见原始速度场与模型预测得出的控制参数所对应的速度场在小失速迎角下一致性较好，在大失速迎角下一致性较差，这是由于在大失速迎角下分离点在机翼较前缘，动态流场对控制参数具有极强的敏感性所致，这与图5(g)所呈现的结果一致，同时该计算误差也与数值计算的精度有关。

图9 原始流场图像与模型预测得出的控制参数所对应流场图像对比

表4 Inception-V3神经网络模型测试结果Table 4 Test results of Inception-V3 convolutional neural network

5 结 论

本文研究了DSJ对翼型分离流场的控制机理与控制规律，通过改进的PSO算法得出了DSJ在一定约束下所能达到的最大升力系数与最小阻力系数，并搭建了Inception-V3卷积神经网络模型对平均速度场进行控制参数识别。研究表明，合成双射流可以对翼型分离流场进行有效控制，其控制机理包括：动量注入效应、涡掺混效应、抽吸效应。Inception-V3卷积神经网络模型在测试算例中控制向量均方误差最大为0.1023，预测误差不超过11%，模型预测得出的控制向量所对应的速度场与原始速度场在小失速迎角下一致性较好，在大失速迎角下一致性较差。

为实现对控制向量与分离流流场性能之间因果关系的精确学习，下一步将通过大涡模拟的方法进行大量数值实验，丰富数据库内容，并采取深度学习的方法，学习控制向量与三维流场图像之间的函数关系，力图学习在三维流场中周期性变化的涡结构，为DSJA的控制律设计与实际工程应用提供进一步的参考。