考虑二次本构关系的湍流模型对翼身组合体阻力预测的影响分析

赵 辉, 张耀冰, 陈江涛, 马明生

(中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000)

0 引 言

飞行器气动力和力矩的精细预测是其设计过程中的关键技术之一。阻力量化和减阻设计对燃料和成本的节省十分关键。Gilyard等[1]指出，对于一架现代宽体远程运输机，在最大起飞重量的情况下，减阻1%每年可以带来$4 000 000的收益，包括燃油的节省和载货量的增加。不同外形之间阻力增量的准确预测是减阻尝试的基础。近些年来计算流体力学(Computational Fluid Dynamics, CFD)在网格生成技术、流场求解和高性能计算机等方面取得了很大的进步，这使得通过数值模拟来评估三维真实运输机外形的气动性能成为可能，CFD预测工业相关外形气动特性的能力得到了广泛的证明[2-5]。然而，对于一些非线性效应主导的流动问题，比如二次流、激波诱导分离等，CFD的预测精度仍然不足[6]。

与此同时，CFD的验证和确认在CFD业界受到广泛的关注。为了评估现有的CFD技术预测工业相关外形气动特性的能力，AIAA应用空气动力学委员会在2001年发起了AIAA阻力预测会议(Drag Prediction Workshop, DPW)，到2016年6月已经成功举办了六届。会议期间，参会者深入讨论了气动力和力矩预测的可靠性。有关会议的细节可以在参考文献[7-11]中查阅。

正如DPW-V的总结报告里展示的一样，当流动是附着流或者分离可以忽略的时候，大部分的数值模拟都可以得到与试验比较一致的结果，满足工业要求。但是CFD预测精度在大迎角区域仍显不足，比如在翼身组合体外形机翼和机身结合处分离流动的预测上，数值模拟的结果跟网格拓扑和疏密分布、湍流模型、黏性项处理等密切相关，分散度很大。很多学者研究发现，基于Bousinessq线性涡黏假设的湍流模型会高估分离区的大小，导致预测的气动力和俯仰力矩与试验值偏差较远。究其原因是线性涡黏模型不能准确预测拐角流动中雷诺应力的各向异性引起的二次流动。在湍流模型中考虑二次本构关系(Quadratic Constitutive Relation, QCR)后，分离区大小和气动特性的预测与试验结果更加吻合。不过以往的研究主要集中在QCR对气动特性预测影响的外在表现上，没有深入分析产生影响的内在机理，而这也是本文的研究重点。

本文对DPW-VI外形进行了数值模拟，着重研究考虑二次本构关系的湍流模型对模拟结果的影响，并深入分析拐角附近的局部流动。重点分析了考虑二次本构关系的湍流模型提高模拟精度的原因和机理，合理地利用该湍流模型能够得到更加合理的压力分布和流动分离情况，对气动特性的预测尤其是阻力预测具有一定的指导意义。

1 计算外形和网格

DPW-VI的外形如图1所示，是NASA和阻力会议组委会联合设计发展的CRM模型。该模型代表了典型现代跨声速运输机外形，设计巡航状态是Ma=0.85，CL=0.5。在NASA NTF风洞、NASA Ames 11-ft风洞和欧洲ETW风洞进行了测试，有大量数据可供CFD确认使用。该模型也是DPW-IV和DPW-V的标模。在DPW-IV[10]和 DPW-V[11]的总结报告中指出，CFD和风洞数据在俯仰力矩曲线上有很大的差异。可能的原因之一是风洞试验模型在测试中因为风载荷发生变形，而CFD计算的外形是没有考虑静气动弹性变形的。因此为了更好地评估CFD水平，组委会将在ETW风洞测量得到的模型静气动弹性变形量考虑了进来，提供了在七个迎角下的变形外形。

(a) 翼身组合体外形

(b) 翼尖的静气动弹性变形

近些年来，非结构网格因为其比较容易处理复杂外形的特点得到了广泛的应用。对于工程外形来说，生成非结构混合网格的时间比生成多块对接结构网格少很多，只用较少的人为干预，网格生成的效率得到极大提高。非结构网格另一个吸引人的方面是可以方便地使用基于流场的网格自适应技术[12]。目前超过一半的阻力会议参与者使用非结构网格进行计算。

本文计算使用的是自行生成的非结构网格，生成过程严格按照组委会提供的网格生成指南进行。四套逐渐加密的网格分别记做Grid T、Grid C、Grid M、Grid F，网格的信息列在表1中。最粗的一套网格的表面网格如图2所示。

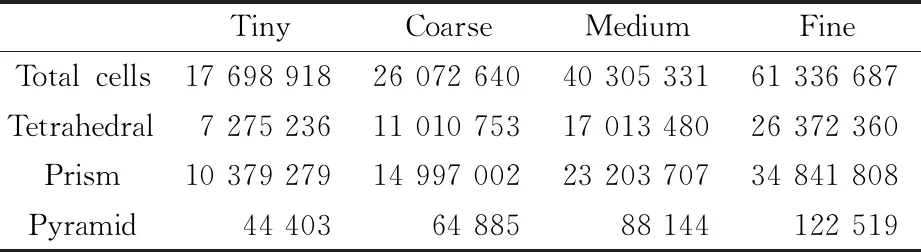
表1 网格量信息Table 1 Information about generated grids

图2 粗网格的表面网格示意图Fig.2 Surface mesh of tiny grid in the grid series

首先为了验证计算程序和网格，使用逐渐加密的四套网格完成定升力CL=0.5状态下的网格收敛性研究。计算的外形是迎角为2.75°下的静气动弹性变形模型。第二个算例是使用中等规模的网格完成静气动弹性影响的预测。迎角从2.5°到4°，以0.25°为间隔。使用的外形是在相应迎角下的静气动弹性变形模型。计算状态为马赫数0.85，基于平均气动弦长的雷诺数为5×106。

2 数值方法

本文计算使用的程序是课题组自行发展的MFlow[13]。该程序采用基于格心的有限体积法，能够处理多种网格单元类型(六面体、四面体、三棱柱、金字塔以及使用几何多重过程中融合产生的多面体)。单元内使用线性重构达到二阶精度。梯度计算使用基于格点的格林高斯方法[14]。使用Venkatakrishnan限制器[15]来抑制间断附近的振荡。使用Roe格式来计算无黏通量。计算使用一阶欧拉后差来推进到收敛状态，使用局部时间步长加速收敛过程。Jacobian通量使用一阶迎风格式得到。使用多重网格来加速收敛。

在方管流动中存在着不可忽视的二次涡流，这些二次流动从拐角区域发展起来，是由拐角附近雷诺应力的梯度诱导产生的。Spalart[16-17]指出传统的Boussinesq线性涡黏假设无法准确地预测雷诺应力的各向异性，即流向、法向和侧向三个方向雷诺应力的区别，因此线性涡黏模型无法准确预测方管内的流动。Spalart借鉴了部分代数雷诺应力的形式，提出了雷诺应力的二次本构关系。新的雷诺应力定义为：

τij,QCR=τij-Cr1[Oikτjk+Ojkτik]-

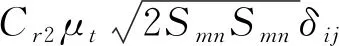
(1)

其中τij是Boussinesq线性涡黏假设给出的雷诺应力，μt是涡黏系数，Oik是无量纲化的旋转张量，定义如下：

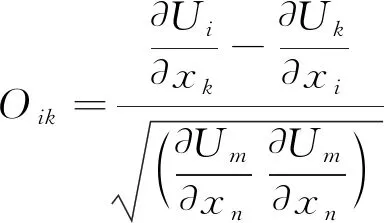
(2)

Smn是应变率张量，定义如下：

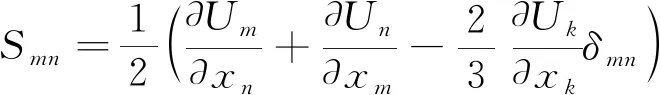
(3)

Cr1和Cr2是模型常数，分别为0.3和2.5。这样给出的雷诺应力τij,QCR并不只是相应的应变率的函数，而是同时考虑了其他方向应变的影响，从而引入雷诺应力的各项异性。

计算中使用SA一方程模型[18]，雷诺应力分别由线性涡黏假设(后续结果中记为SA)和二次本构关系(记为SA_QCR)给出。本文的计算从自由来流开始，假定流动为全湍流。图3为本文计算的残差收敛和气动力变化曲线，所有计算密度的残差都下降了两个量级以上，气动力的振荡在0.2%以内。

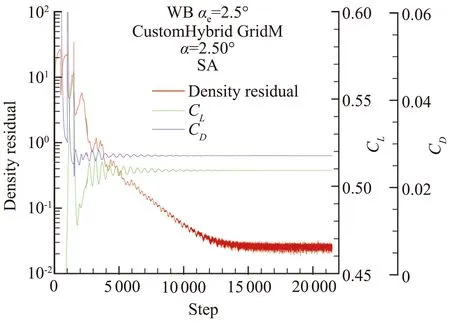
图3 连续方程的残差和气动力的收敛曲线Fig.3 Convergence of density residual and force and moment coefficient

3 结果和讨论

3.1 定升力系数下的网格收敛性研究

本节中展示了定升力条件下的网格收敛性，结果如图4所示。横坐标是N-2/3,N代表网格单元总数，N-2/3代表网格特征尺度的平方，纵坐标中CD代表总的阻力，CDP和CDV分别代表压差阻力系数和摩擦阻力系数，Cm代表俯仰力矩系数。MFlow在空间为二阶精度，因此如果网格位于收敛的渐近区域，气动力和力矩有线性的收敛特性。除了最粗的网格，升阻力和俯仰力矩有近似线性的网格收敛性，证实流场解位于渐近解区域。压差阻力随着网格加密减小，摩擦阻力增大，总阻力减小。摩擦阻力随着网格变化不大，表明网格加密到一定程度后便可以准确捕捉边界层。

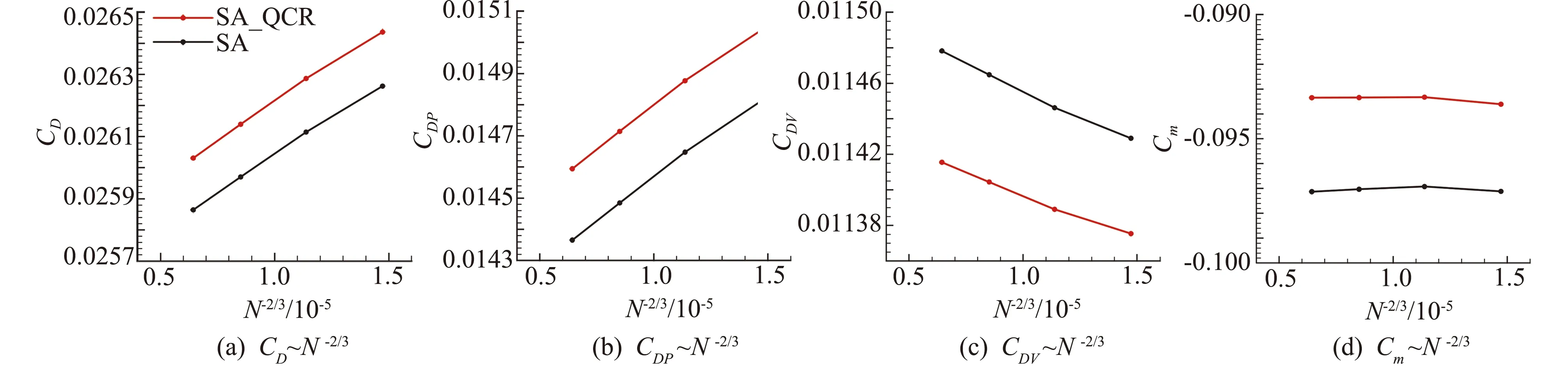
图4 定升力CL=0.5条件下网格收敛性曲线Fig.4 Grid-convergence properties under the lift condition of CL=0.5

SA_QCR计算结果的规律跟SA模型的计算结果规律非常一致，在使用同一套网格的情况下，两者的结果只是有一个随网格变化很小的平移量。SA_QCR得到的总阻力比SA大1.7cnts左右，其中压差阻力大2.3cnts，摩擦阻力小约0.6cnts(cnt为阻力系数单位，1cnt=0.0001)。

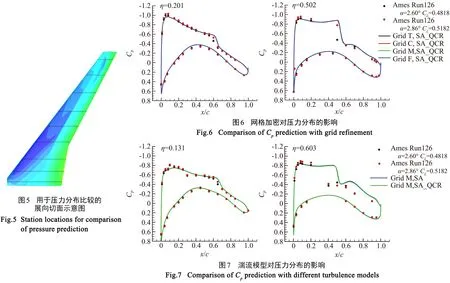
针对机翼不同站位的压力分布情况，一般选取9个典型的展向站位进行分析，如图5所示，不同站位到对称面的距离占机翼展长的百分比分别为0.131、0.201、0.283、0.397、0.502、0.603、0.727、0.846、0.950，包含了翼根、翼中间和翼尖三个不同的区域。

如图6和图7所示，本文分别选取两个典型站位展示网格加密和湍流模型对压力分布的影响。该迎角下，流动基本没有分离，随着网格加密，压力分布变化不大。在激波附近，网格越密，激波越陡。计算的吸力峰比试验低，很可能是计算的迎角比试验低的缘故。从η=0.603界面开始预测的激波位置偏后。QCR修正使得激波位置稍稍前移，吸力峰更高一点。

可以用Cfx的分布来研究壁面的分离情况，如图8所示。蓝色的区域表示负的Cfx，用来近似表征流动分离。QCR修正使得翼身结合处的分离区域大大减小，网格加密使得分离变大。但总的来说，分离泡的尺寸很小，流向长度不大于当地弦长的4%。

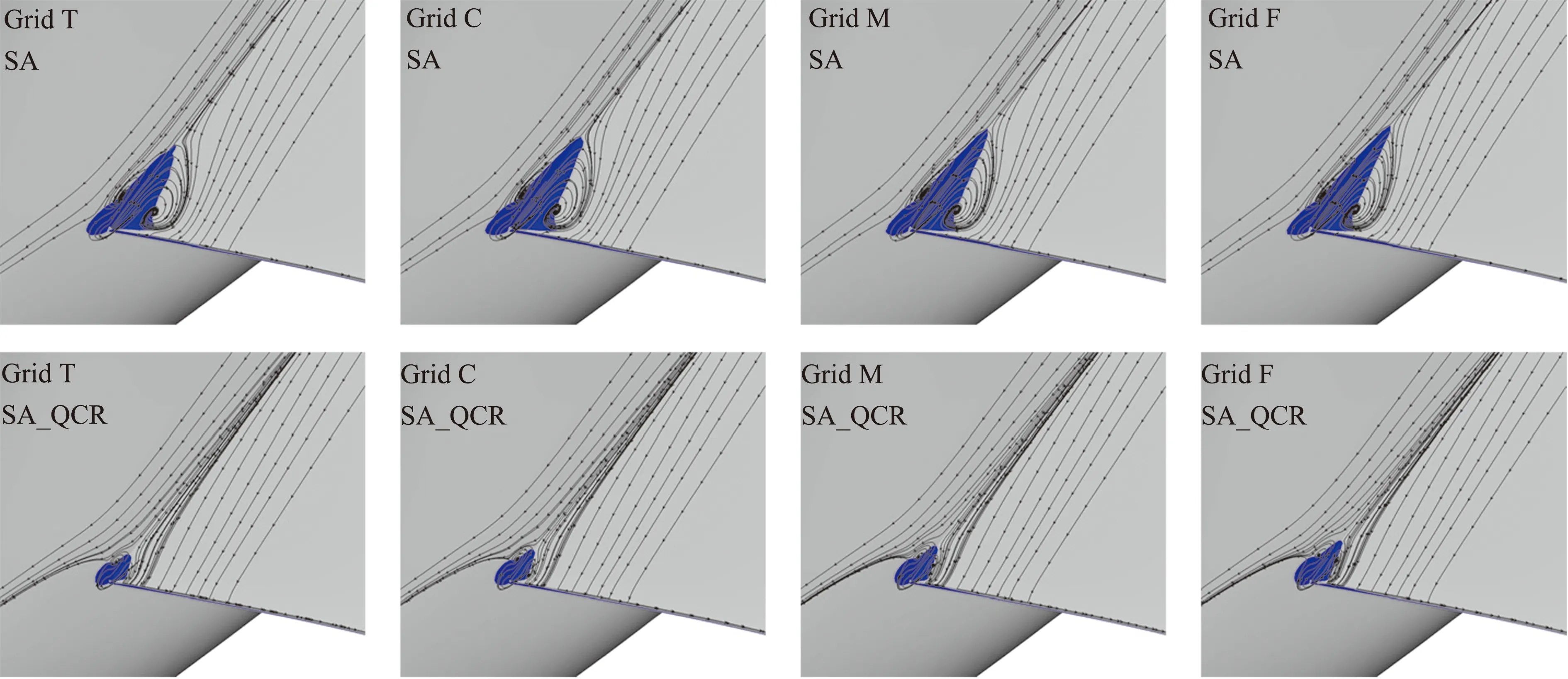
图8 表面流线和Cfx云图比较Fig.8 Comparison of surface streamlines and contours of Cfx

3.2 CRM WB抖振特性预测

从图9(a)的升力系数曲线可以看到，在迎角3.5°处，SA出现了比较明显的提前的流动分离，升力系数开始转而下降。随着迎角继续增大，升力系数又开始爬升，在迎角3.75°处升力线拐折，斜率减小。相对于原始SA模型，QCR在迎角2.5°～3.0°之间对升力预测的影响相对较小。在更大的迎角下，QCR修正对计算结果影响很大。QCR预测的升力系数跟试验趋势一致，只是有一个随迎角变化不大的平移量。

图9(b)为阻力系数的预测情况。SA_QCR计算得到的阻力系数跟试验的规律基本一致，比试验值稍大约30～40cnts。原始的SA模型在迎角3.5°开始出现明显的斜率变小。在极曲线上，由于升力系数在迎角3.5°出现的拐折，原始SA模型出现了明显的下降再上升的过程。SA_QCR结果跟试验趋势一致。

同样的，SA_QCR预测的俯仰力矩系数跟试验规律比较一致，如图9(c)，但是预测的力矩过于低头。有学者指出，考虑支架干扰会进一步改善俯仰力矩的预测。

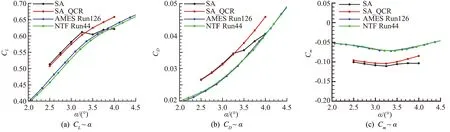
图9 湍流模型对气动特性预测的影响Fig.9 Effect of different turbulence models on the prediction of aerodynamic properties

从迎角3.5°开始，SA计算结果背离试验的趋势，而SA_QCR的结果一直跟试验趋势比较吻合。从图10(a)的3.5°迎角下的压力分布可以看出，SA_QCR的预测大体上令人满意。在靠近翼根的截面，原始SA模型计算出现了激波位置大大靠前、激波后流动分离的现象。从图10(b)整个机翼的压力分布云图可以清楚的看出，原始模型的结果，在靠近翼根区域，激波位置更加靠前。

图10(c)给出了表面流线和Cfx云图。原始的SA模型在翼身结合处出现了比较大的分离，而在QCR的结果中，此处的分离几乎不可见。QCR在机翼中部激波后的分离要大得多。

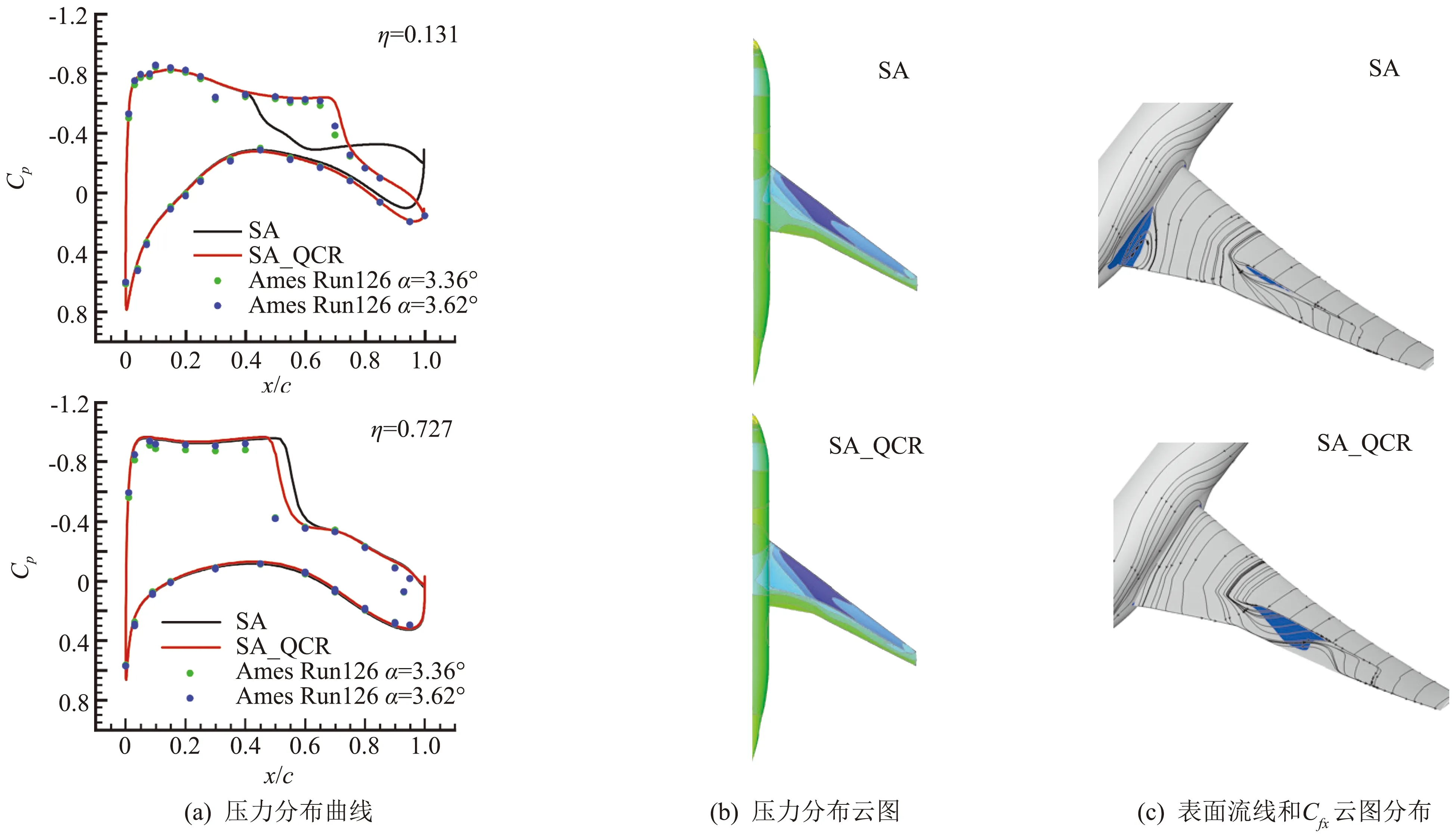
图10 在迎角3.5°下，SA与SQ_QCR湍流模型对流场模拟的比较Fig.10 Comparison of SA and SA_QCR turbulence models for flow field simulations at 3.5° of angle of attack

翼根处的分离同样可以从η=0.131截面处的马赫数云图和平面流线清楚地看到，如图11所示。使用原始SA模型时，流动在流向遇到很大的逆压梯度进而分离，形成较大的分离区，减弱了分离点之前流体微团的能量。而使用QCR之后，流动一直保持附着流动。

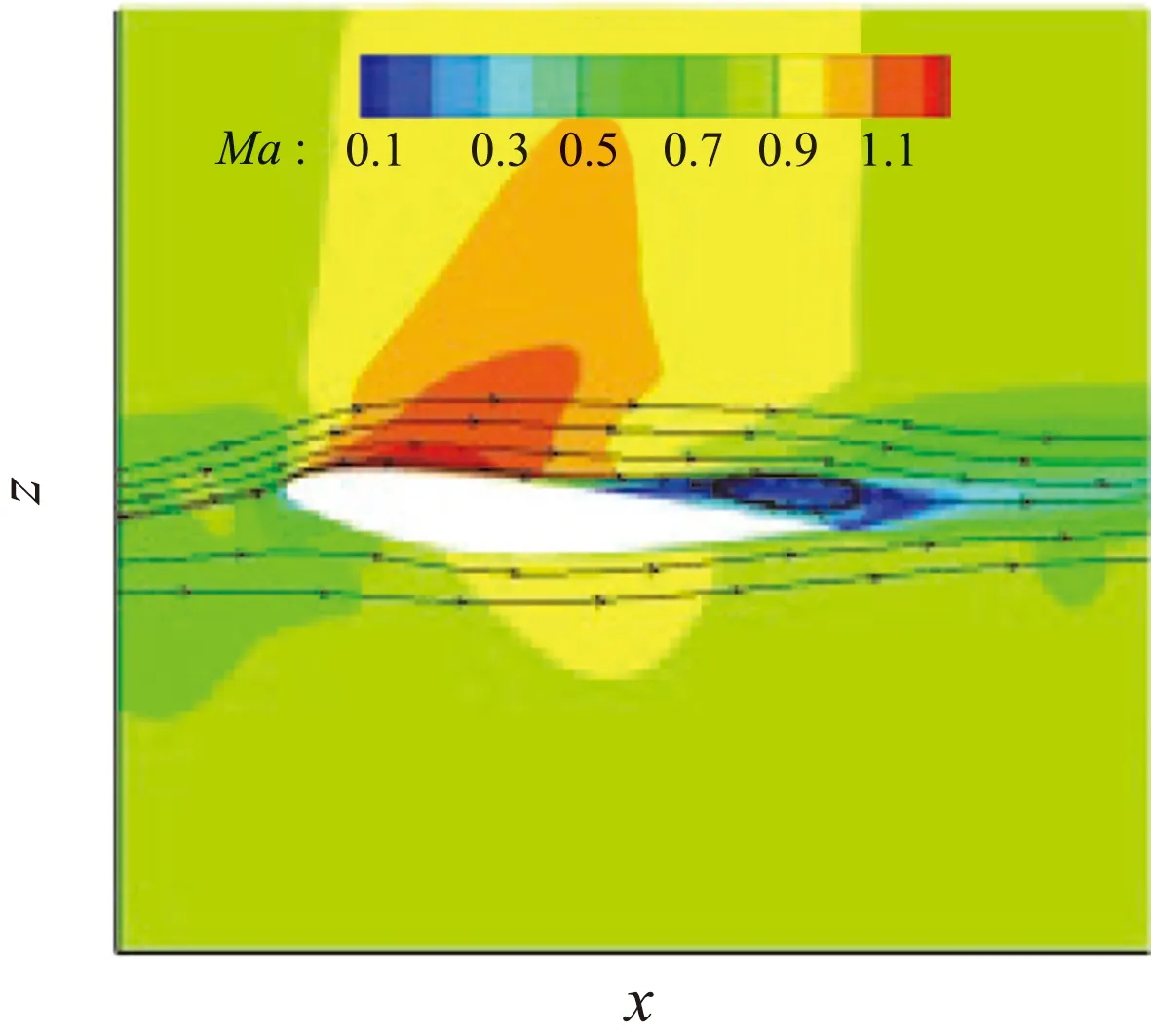
(a) SA

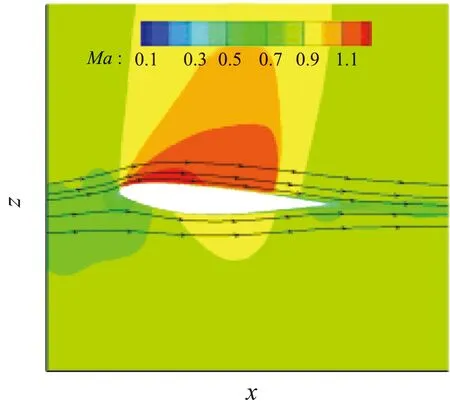
(b) SA_QCR

为了深入分析QCR对翼身结合处拐角流动的影响，取机翼中弦处等流向截面来研究局部的流动现象。图12给出了机翼表面的压力分布沿机翼展向的变化。在翼身结合处，原始SA模型得到的压力比QCR的结果大很多。为了进一步分析SA模型得到更大逆压梯度的原因，图13给出了拐角处涡量流向分量ωx的云图，红色和绿色分别代表符号相反的ωx区域。在原始SA模型的结果中，在拐角的机翼一侧ωx为负。使用QCR后，贴近壁面处ωx为负，离开壁面一定距离后ωx为正，在两者相互作用下，当地壁面的压力不如原始SA模型的大。Spalart指出QCR会提高管道流动中二次流模拟的精度。在本文算例中，与试验结果相比，QCR得到了更加合理的压力分布和流动分离情况，也提高了气动特性的预测。

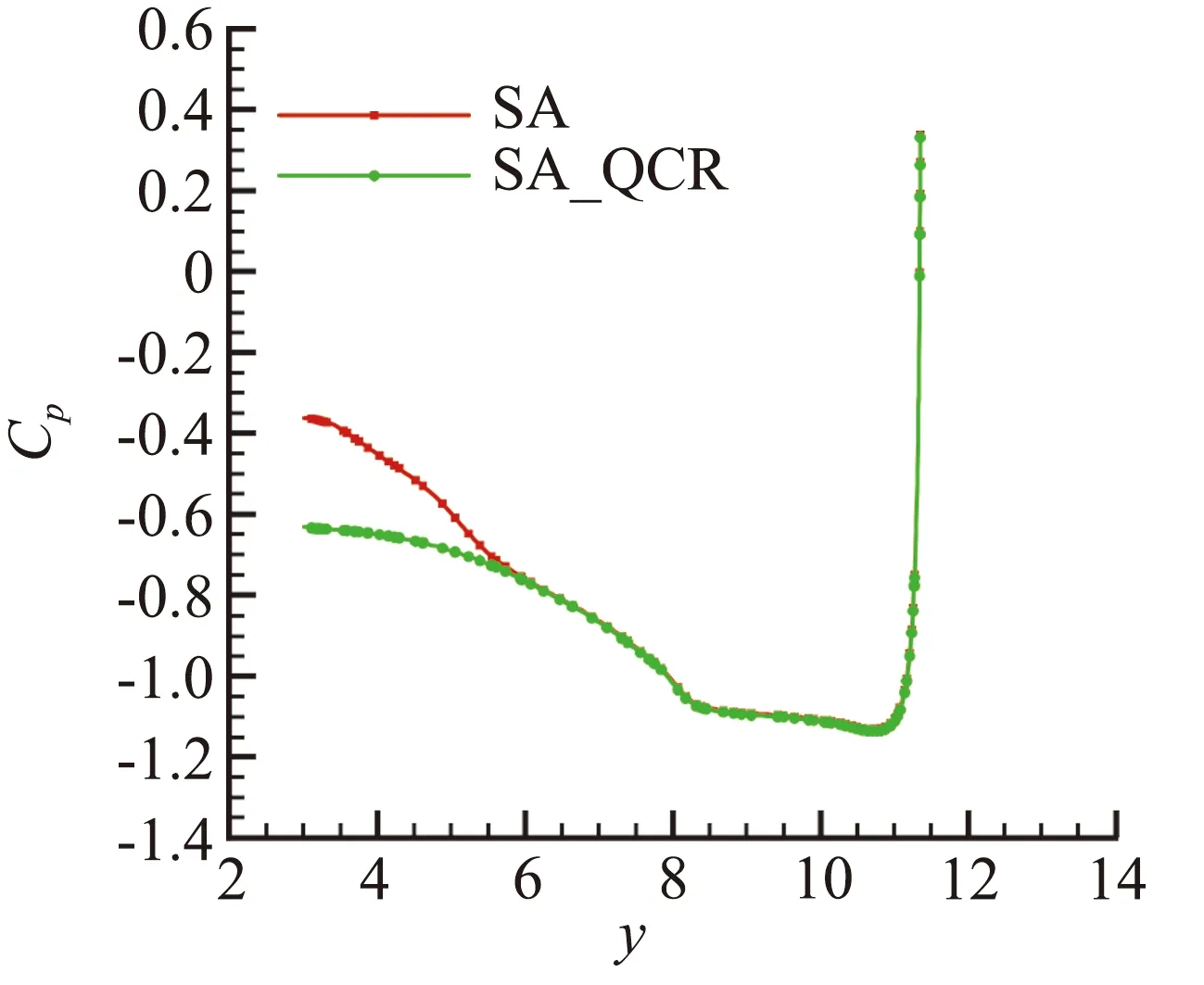
图12 机翼中弦处压力分布沿机翼展向的变化Fig.12 Comparison of Cp along spanwise direction

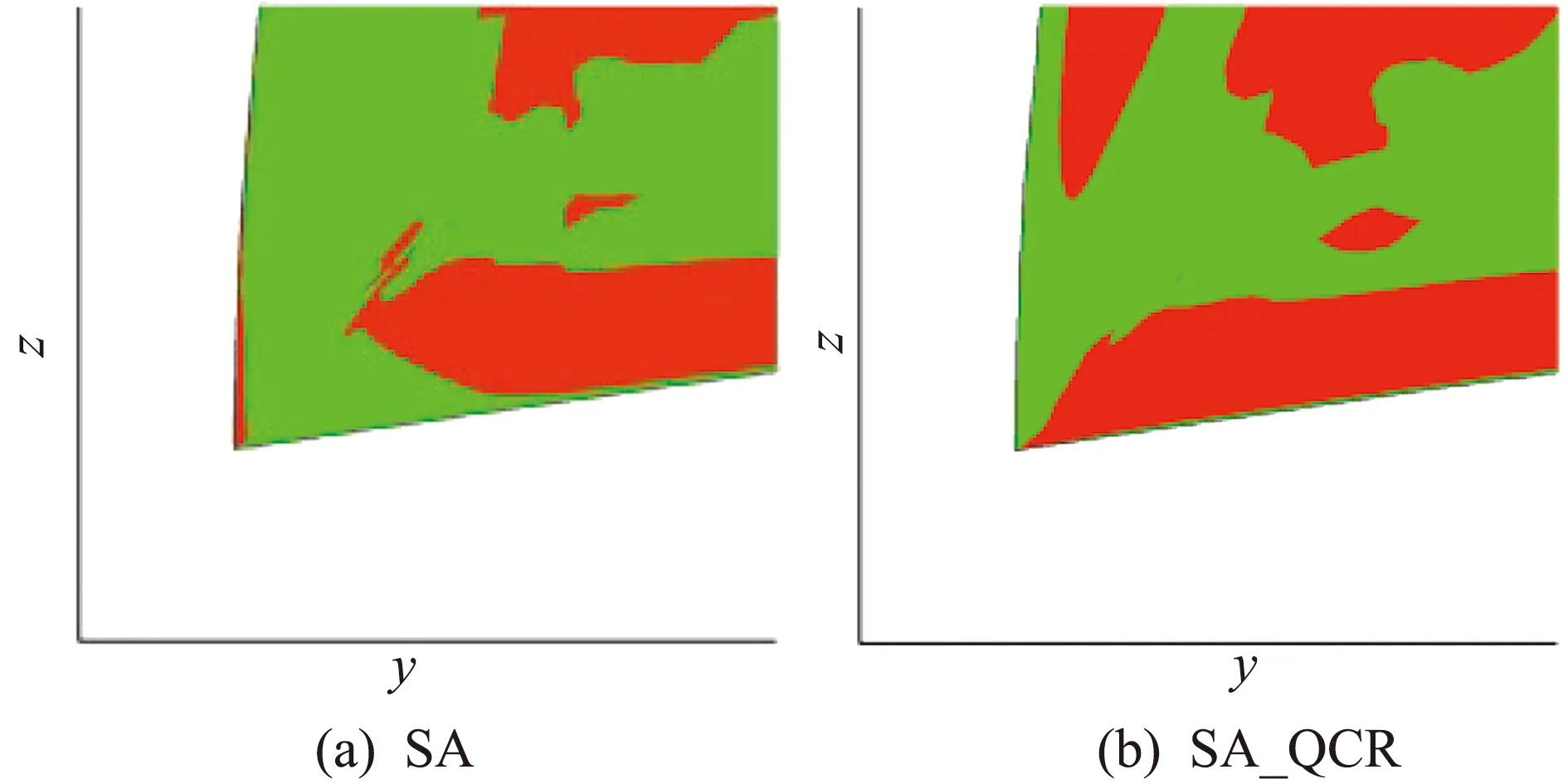
图13 机翼中弦处ωx分布云图比较Fig.13 Comparison of ωxdistribution at the middle of wing

4 结 论

本文使用自行发展的MFlow求解器对第六届AIAA阻力预测会议的翼身组合体外形进行了数值模拟研究。

在CL=0.5条件下，数值模拟得到的气动力和力矩有线性的网格收敛特性，证实流场解位于渐近解区域。线性涡黏模型和考虑二次本构关系的湍流模型的结果差别不大。但是随着迎角增大，线性涡黏模型的结果在翼身结合处一个很大的分离涡，这也导致了预测的升力系数和阻力系数曲线出现明显的拐折。使用考虑二次本构关系的湍流模型计算，翼身结合处的分离涡几乎不可见，这与试验更加吻合，预测的气动力和力矩也跟试验趋势一致。

对翼身结合处局部二次流动的详细分析展示了考虑二次本构关系的湍流模型提高模拟精度的原因。在使用QCR模型后，非常贴近壁面处和离开壁面一定距离处有相反的ωx，在两者相互作用下，当地壁面的压力不如原始SA模型大。QCR修正对二次流模拟精度的提高，得到了更加合理的压力分布和流动分离情况，也提高了气动特性的预测。

本文仅从局部流动分析入手，有效验证了QCR模型在工程应用上的潜力，下一步将会在模型层面对其进行探讨，分析规律。