考虑到站时间可靠性的有限公交优先信号控制

赵天羽, 梁士栋, 徐 晗, 张子毅, 杜豪赫

(上海理工大学 管理学院, 上海200093)

0 引 言

随着中国各级政府对公共交通资金投入增加和政策扶持力度的增大,公共交通体系建设得以快速发展。 针对目前交通情况,倡导公交优先出行的方案是缓解交通压力的有效方法。 传统的公交优先策略是简单的单点交叉口公交优先的信号控制策略［1-4］,即根据公交车在该段线路上的行驶的速率、乘客分布及数量,线路上过往车辆及垂直交叉口小汽车的分布等历史数据,在信号交叉口设置一个特定的信号灯配时,以给予公交车优先权。 在传统控制策略在初始阶段收到了一定的成效,但在随后的公交运营中出现了垂直交叉口过往车辆滞留时间过长的现象。 此外,这种控制方法针对性不强,公交车在道路上会遇到公交到站停车、礼让行人、乘客上下车时间较难把握等情况,使得每辆公交车在实际行驶过程中车头时距发生改变,简单的单点交叉口公交优先的信号控制策略不能根据每辆公交车的车头时距做出灵活的调节。 近年来,根据公交车到达交叉口的距离自动改变交通信号灯的配时和周期,可以保证每一辆公交车尽快到达下一站。 但是,这种传统的调控方式造成了公交串车现象［5-6］,公交簇拥现象［7］等一系列不良现象。 大多数调控方法只是考虑单一的公交车在道路上的运行［8-9］,却忽略了公交系统整体的运行效果,这使得公交车之间没有联系,公交车的优势并没有被充分挖掘。

本文的研究主要内容是：在每一辆公交车到达信号灯交叉口之前的一个特定位置,通过输入公交车的行驶速度与路况信息,对其到达交叉口的时间及车头时距做出预估,并将预估车头时距与期望车头时距做出比较。 若小于期望值,则通过实时改变信号灯的配时,尽可能减缓公交车通过。 若大于期望值,则通过实时改变信号灯的配时,尽可能减少公交车在交叉口的延误时间。 这样的信号灯调控方法根据公交车实时时空运行信息,兼顾公交系统本身运行秩序,让公交有限优先。

1 问题描述

本文在信号交叉口处所使用的控制策略主要包括4 种：红灯早断、红灯延长、绿灯早断、绿灯延长。根据公交车到达交叉口车头时距的不同情况采取不同方案进行调控。 要求控制模型满足如下假设：

(1)公交车只在公交车专用道上行驶。

(2)公交车在理想状态下到达交叉口,不考虑社会车辆及行人对公交车的影响。

(3)在公交车到达交叉口时,信号灯只在信号灯所在的周期内进行调控。

(4)在一个信号灯周期内,按照先绿灯后红灯的条件进行。

典型信号周期内信号控制形式：红灯早断与红灯延长,绿灯早断与绿灯延长。 控制形式的实施机理过程如图1 所示,其中图1(a)为红灯早断与红灯延长,其中图1(b)为绿灯早断与绿灯延长。

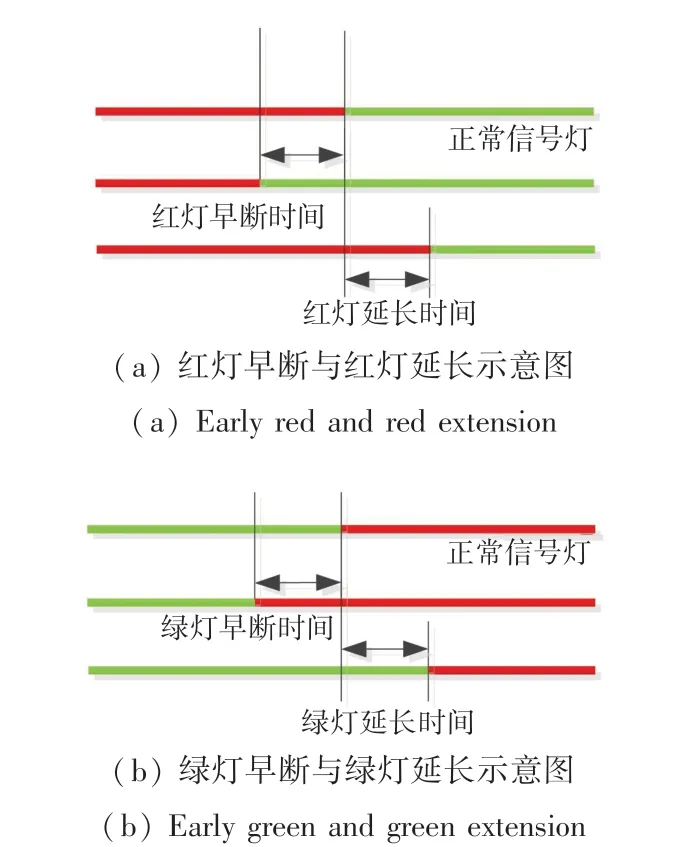
图1 交叉口信号控制形式示意图Fig. 1 Control strategy for the signalized intersection

1.1 公交车到达交叉口时间估计及目标信号周期识别

如图2 所示,截面1,截面2 以及两截面之间的信号交叉口部分为本文的研究对象。 根据预测公交车车头时距调整信号灯控制方案,首先对公交车到达信号交叉口的时间进行计算。 截面1 为检测器位置,当第i 辆公交车行驶至截面1 时,定义此时的时刻为Tin,i。 当该公交车行驶至交叉口停车线时,定义该时刻为Ta,i。

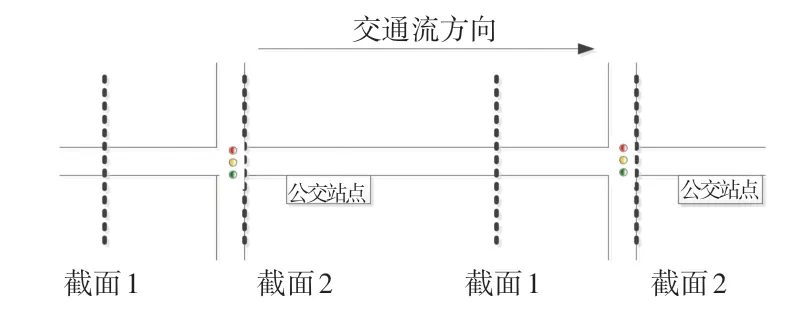
图2 公交运行过程及信号控制区域示意图Fig. 2 Operation process of buses and signal control area near intersection

根据假设,公交车在公交专用道上行驶时速度变化较小,设为定值V。 截面1 和信号交叉口之间的距离为L。 根据经典运动学公式可知,到达信号交叉口处的时刻如公式(1)所示。

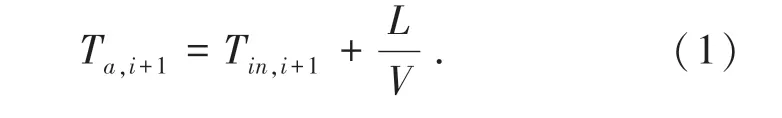
为了使信号配时得以重新优化,应判断公交车到达交叉口处的时刻所处的周期。 定义信号交叉口的信号周期时长为C,当公交车到达交叉口的时间大于n 倍的C 且小于n ＋1 倍的C 时,则可以判定公交车到达交叉口时位于信号灯的第n ＋1 个周期内,如公式(2) 所示。 对该周期内的信号灯时长进行调整。

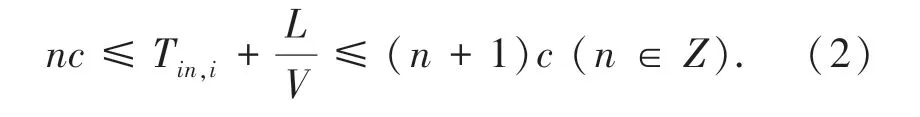
公交车在公交专用道上按照交通流方向行驶,且公交车上装有发信器。 为检测公交车通过截面1的时刻,预测公交车到达交叉口的时刻,并调整公交车通过交叉口的时刻(即公交车通过截面2 的时刻)。 交叉口的交通信号灯可以根据截面1 处接收器反馈的信号临时改变交通信号灯的配时,改变公交车到达交叉口时的运行状态。

以图2 为例,截面1 到达交叉口的距离L 不宜过长也不宜过短。 如果距离短,交叉口信号灯无法及时处理由截面1 处检测器反馈的信息,进而无法形成对公交车的调控效果；如果距离过长,则交叉口信号灯调控的时间变化过大,无法被公交车完全利用。 建议L 的距离为60 m～150 m 之间［10］。 当截面1 的检测器检测到公交车通过截面1 时,将信息反馈到交叉口信号灯控制后台［11］,后台再根据估计的公交车车头时距与理想的车头时距进行对比,选出最优调控方案,并实时调控信号灯的状态,使公交车通过交叉口之后的车头时距更接近理想车头时距。

1.2 公交车头时距计算模型

定义hi为第i 辆公交车的车头时距。 (后一辆公交车相对于前一辆公交车到达截面2 的时刻的差值)

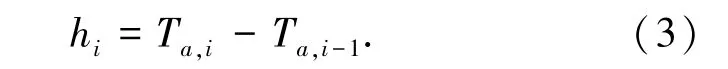
通过给定的标准车头时距H, 调控信号灯的配时,使整条公交运营线路上的公交车的车头时距向标准车头时距H 收敛,从而提高整条公交运营线路上公交车运营的效率。 如公式(4)所示。

定义D 为信号灯可调控状态下公交车在交叉口相较于信号灯正常状态下延误时长,延误时长与交叉口的红灯时长r 和绿灯时长g 有关,构建公交车的延误时长与红灯(r) 和绿灯的函数关系公式(5) 所示。

2 信号配时优化模型及控制算法

2.1 信号配时优化模型

当第i 辆公交车到达截面1 时,预测第i 辆公交车与第i-1 辆公交车通过截面2 时的时间,即第i 辆公交车的车头时距。 根据第i 辆公交车到达截面1时的行驶速度,预测该公交车到达交叉口时信号灯的运行的时间。 并根据预测的车头时距与标准车头时距的偏差,改变信号配时,规则如下：

Case 1在不改变信号配时的情况下,期望的车头时距满足公式(4) hi= H 的判断标准,则不改变信号灯的原有配时,使得公交车到达交叉口时按照原信号灯配时通行。

Case 2当hi＞H 且交叉口信号灯为绿灯时。

当预测车头时距h～i 大于标准车头时距时,说明公交车i 行驶速度小于期望,应该加快公交行驶速度,由于此时信号交叉口已经处于绿灯,无法进一步加快公交运行速度。 为保证公交车运营效率,则不改变信号灯配时,公交车直接通过,延误为0,如公式(6)所示。

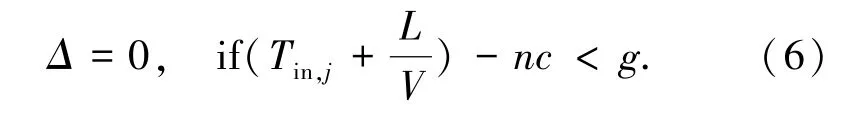
Case 3当hi≤H 且交叉口信号灯为绿灯时。

由于交叉口信号灯为单点控制,即调控只在公交车到达交叉口时,信号灯正在进行的周期内完成。则需要对比在不调控和绿灯早断两种不同方案,选择优化效果更显著的方案进行调配。

当公交车在不调控的情况下,优化效果显著于绿灯早断的优化效果,则采用信号灯不调控,信号灯改变时间如公式(7)所示。

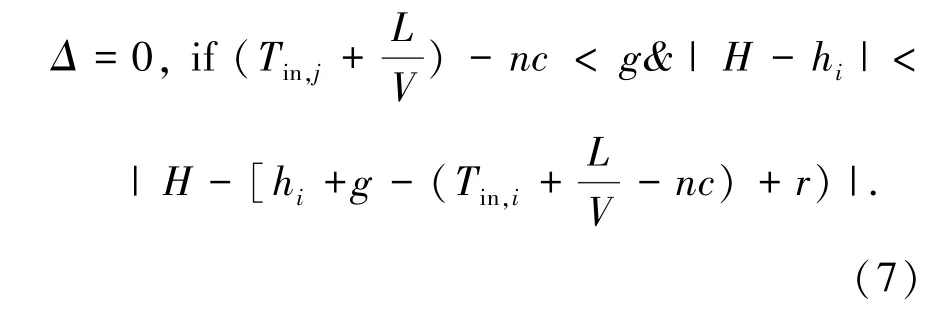
当公交车在采用绿灯早断的情况下,优化效果显著于不调控的优化效果,则采用绿灯早断,早断时间如公式(8)所示。

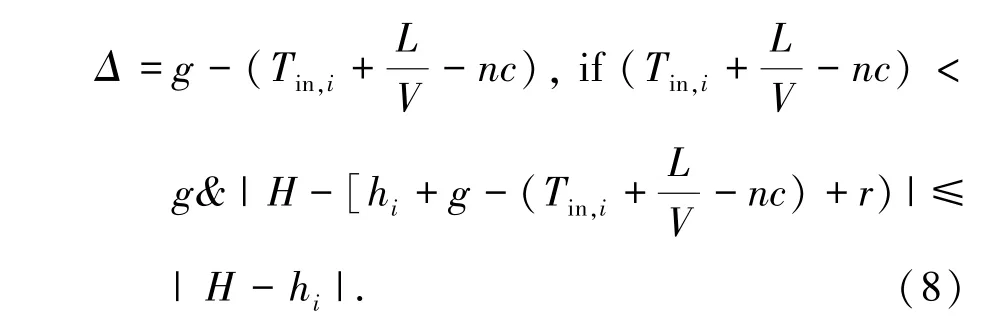
Case 4当hi＞H 且交叉口信号灯为红灯时。

为保证公交车运营效率,不使该公交车的车头时距与目标车头时距进一步扩大,需要把交叉口的信号灯改为绿灯。 需要对比在绿灯延长与红灯早断两种不同控制方案,选择优化效果更显著的方案进行调配。

当绿灯延长相较于原信号配时改动方案比红灯早断相较于原信号配时改动方案改动幅度小时,采用绿灯延长,延长时间如公式(9)所示。

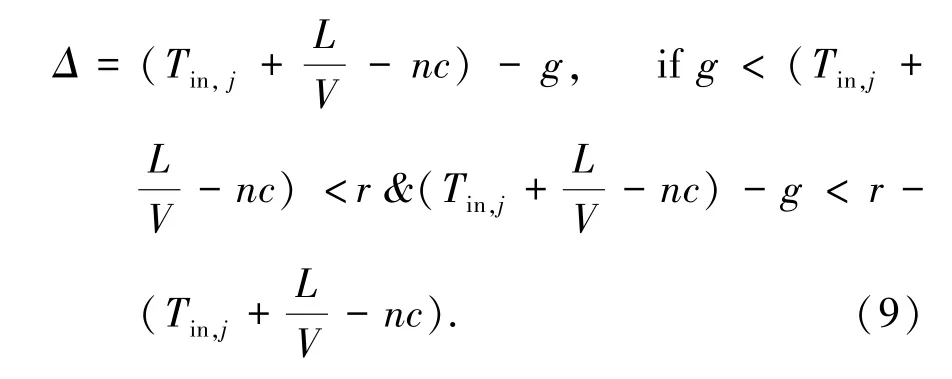
当红灯早断相较于原信号配时改动方案比绿灯延长相较于原信号配时改动方案改动幅度小时,采用红灯早断,早断时间如公式(10)所示。

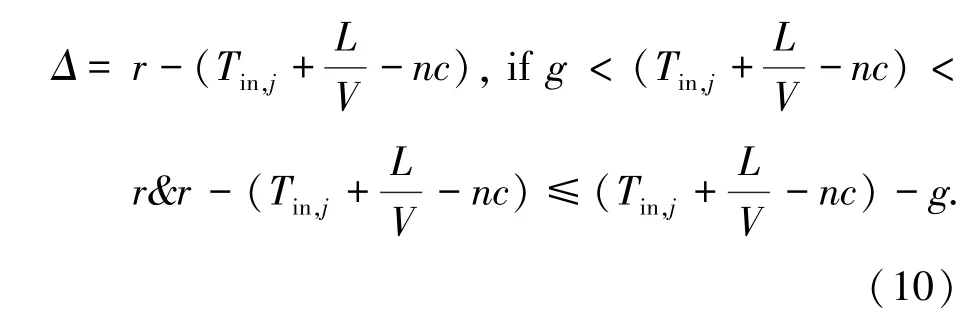
Case 5当hi≤H 且交叉口信号灯为红灯时。

为保证提高公交运营效率,需要判断公交车所需要的延误时间是否能在公交车到达交叉口时红灯剩余的时长内完成。

当公交车所需要的延误时间能在公交车到达交叉口时红灯剩余的时长内完成时,采用红灯早断。早断时间如公式(11)所示。

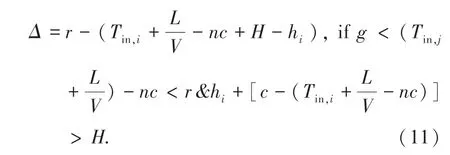
当公交车所需要的延误时间不能在公交车到达交叉口时红灯剩余的时长内完成时,采用红灯延长。延长时间如公式(12)所示。

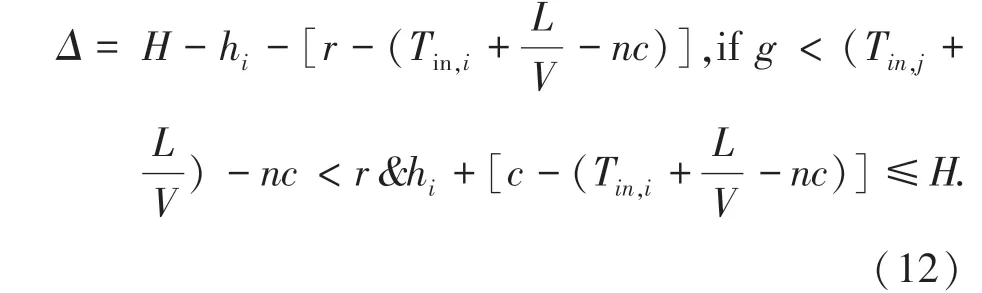
2.2 约束条件

定义典型信号周期内信号控制应保证交叉口以及垂直交叉口行人顺利通过,即红灯早断与红灯延长,绿灯早断与绿灯延长都应该控制在一定范围内,需要设置最小绿灯时间Gmin。

绿灯早断的时间的范围如公式(13)所示。

2.3 公交有限信号优先控制流程图

当公交车到达交叉口时,车头时距满足公式(3),即不改变信号灯配时,故不在流程图中展示。

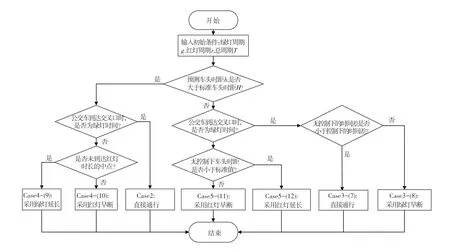
图3 公交配时调控流程图Fig. 3 Flow chart of optimal signal control for buses

3 模拟验证

本文用C 语言搭建仿真平台,模拟公交车在交叉口运行情况,验证本文提出的信号优先控制方法的有效性及可靠性,并对信号周期做进一步敏感性分析。 本文验证部分选择图2 中截面1 与截面2 之间的单向道路区间为实验对象。 假设公交车在公交车专用道上行驶,与道路上的小汽车相对独立。 在正常状态下交叉口信号灯的周期为180 s,按照先绿灯90 s 后红灯90 s 的顺序进行。 在本文的信号控制中,约束条件最短绿灯时间为10 s。

用100 个随机生成的公交车车头时距进行测试,100 个公交车车头时距均值为199 s,车头时距标准差为28 s,测试结果如图4 所示。 在经过正常红绿灯调控的情况下通过交叉口之后,实验中100 辆公交车的车头时距标准差变成了43 s,而经过本文提出的方案进行调控下的公交车通过交叉口之后,实验中100 s公交车的车头时距标准差变成了26 s,即公交车在经过本文提出的方案调控下,公交车的车头时距波动幅度较小,公交车的车头时距更均衡。 公交车的服务水平在本文提出的控制方案下有了明显的提高。

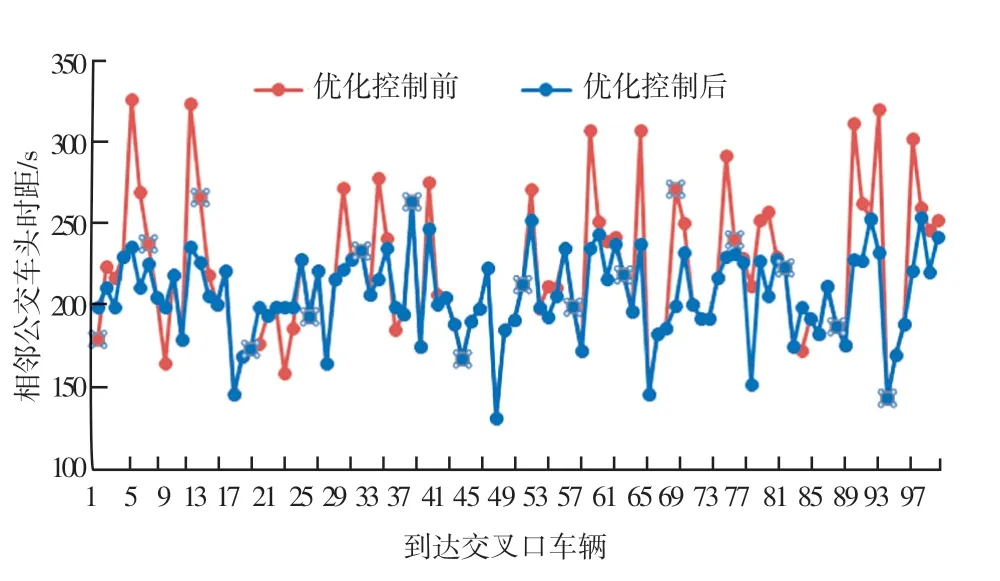
图4 调控前后输出车头时距对比图Fig. 4 Comparison of the headway fluctuation using optimal control method and original plan

为了更直观地体现本文提出的信号灯调控方案能降低车头时距的标准差,继续对以上100 个随机生成的公交车车头时距进行分析。 数据显示,在未经调控的信号灯下通过交叉口之后,实验中100 辆公交车的车头时距均落入130 s 至330 s 之间。 在本文提出的方案进行调控下的公交车通过交叉口之后,100 辆公交车的车头时距也全部落入130 s 至330 s 之间。 于是本次分析打算将130 s 至330 s 之间,等分成20 份(即每连续十秒为一个区间)。 将以上两组车头时距分别放入对应的区间内,比较同一个区间内调控前后的车头时距分别出现的频次,并形成柱状图,如下图5 所示。

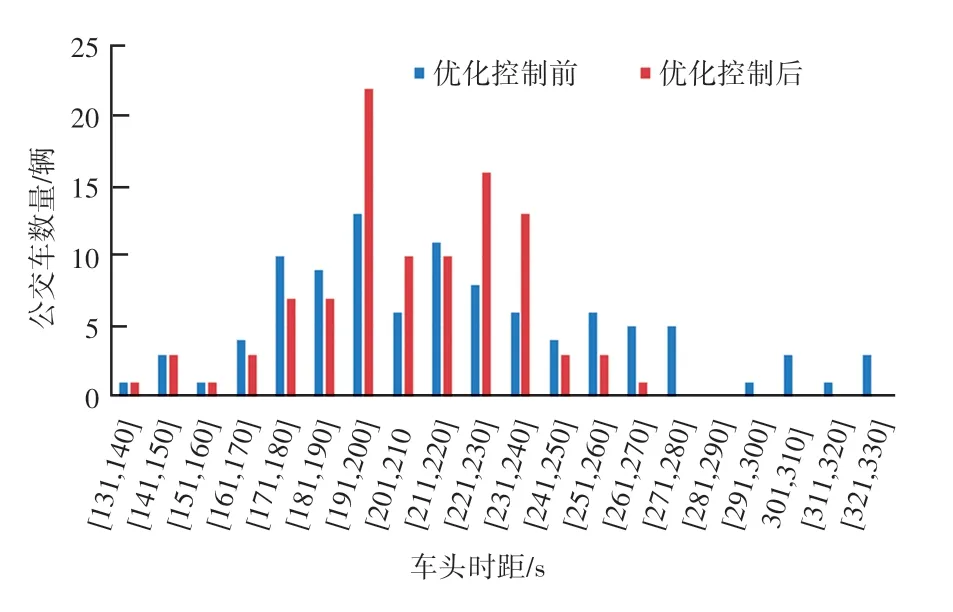
图5 调控前后车头时距频数分布图Fig. 5 Comparison of headway frequency between two scenes

在车头时距170 s 到240 s 之间,可认为落入该区间的车头时距与期望车头时距相比,偏差较小。未经信号灯调控的车头时距中,落入该区间的车头时距共为67 个,占总体的67%。 而经过信号灯调控后,在该区间的车头时距共为88 个,占总体的88%。相比,经过信号灯调控过后,有更多的车头时距靠近均值。 对于该分布的左尾与右尾区间(即在车头时距131 s 至170 s 之间与车头时距240 s 至330 s 之间),可认为偏离期望车头时距较大。 未经信号灯调控的车头时距中,落入该区间的车头时距共为33个,占总体的33%。 而经过信号灯调控后,在该区间的车头时距共22 个,占总体的22%。 相比,经过信号灯调控过后,极端值的数量显著降低。 柱状图更直观地反映出信号灯调控方案能降低车头时距的标准差,使其达到在均值附近稳定的状态。

此外,验证部分还对信号周期进行了敏感性分析。 取周期为10 s 作为最短周期,每10 s 作为一个单位,直到周期为300 s 进行研究。 研究表明：公交车在不同的交叉口信号周期下通过交叉口之后的车头时距不同。 公交车在两种信号调控下通过交叉口之后的车头时距标准差如图6 所示。

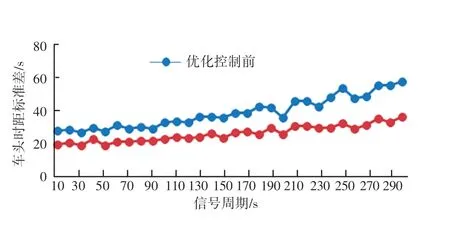
图6 调控前后输出车头时距的标准差随周期变化图Fig. 6 Numerical analysis of headway standard deviation with increasing of signal cycle

随着交叉口信号灯周期时间的增长,公交车通过交叉口后的车头时距标准差呈明显上升趋势。 而在相同的到达截面1 时间的条件下,经过调控下的公交车通过交叉口之后的车头时距标准差明显低于未经过任何调控的公交车通过交叉口的车头时距标准差。

调控的关键在于公交车到达截面1 时,预测公交车到达交叉口时交叉口信号灯的状况,并根据车头时距的实际情况,交叉口的信号灯做出相应的调控,使公交线路的车头时距达到均衡。 如果调控预测准确,公交车在调控下通过交叉口的车头时距的标准差一定小于公交车未经调控后通过交叉口的车头时距的标准差。 模拟期间的100 辆公交车,无公交车采用绿灯早断, 11 辆公交车采用了绿灯延长,25 辆公交车采用了红灯早断,10 辆公交车采用了红灯延长。 总体而言,模拟验证期间有46%的公交车通过交叉口时,信号灯配时改变。 而公交车通过信号配时改变的交叉口后的车头时距标准差相较于未经调控的公交车通过交叉口后的车头时距标准差下降了17 s,下降了约39.54%。 由此表明预测调控方案理想状况下运行的可靠性。

4 结束语

本文通过公交车经过交叉口前的某一固定截面,根据公交车在公交车专用道上的行驶速度预测公交车到达交叉口的时间及到达交叉口时信号灯的运行状况,根据公交车到达交叉口时的车头时距的实际情况,改变交叉口的信号配时,使通过交叉口的公交车的车头时距收敛于某一给定的固定值,从而使公交车的运营的效率提高。 采用C 语言编程模拟公交车随机到达交叉口的时间,以及交叉口信号灯配时的改变。 实验结果表明调控方案具有较高的可靠性,能使通过交叉口的公交车的车头时距达到均衡,改善公交运营服务的可靠性。