一种RFID 标签估算方法

雷隆毓, 周向阳

(贵州大学 电气工程学院, 贵阳50025)

0 引 言

无线射频识别技术 RFID(Radio Frequency Identi-fication)是一种自动识别技术,该技术具有许多优点,如抗干扰能力强、信息量大等。 但在RFID系统中,读写器可识别的范围内,极容易出现多个标签同时返回阅读器的请求,从而发生信息碰撞,使得阅读器无法识别到碰撞标签,甚至会出现“标签饥饿”的情形。 如何在提高系统有效识别率和吞吐量的情况下解决标签间的碰撞,成为多标签防碰撞最为核心的问题。 因天线系统、读写器、标签成本和实际实现问题,空分多址,码分多址,频分多址三种访问接入方法不适用于实际使用操作,因此RFID 系统通常使用时分多址方式进行数据通信［1］。

时分多址访问接入方式的多标签防碰撞算法分为两种：一种是非确定性的ALOHA 算法,具体可分为：纯ALOHA 算法、时隙ALOHA(Slotted ALOHA,SA)算法、帧时隙ALOHA(Frame-Slotted ALOHA,FSA)算法、动态帧时隙ALOHA(Dynamic Frame-SlottedALOHA, DFSA) 算 法、 改 进 动 态 帧 时 隙ALOHA(Modi-fied Dynamic Frame- Slotted ALOHA,MDFSA)、分组动态帧时隙ALOHA(Group Dynamic Frame- SlottedALOHA,GDFSA)算法。 对于另一种确定型的二进制树算法,因能保证所有的标签排列识别,而不会出现“标签饥饿”的问题,但会因为阅读器与标签之间的通信信息量,导致查询全部的标签需要时间较长,系统负荷量大。 因等待时间过长,使得标签丢失量变大。 而概率型的ALOHA 算法对标签的要求相对较低,但不确定的随机性,会出现“标签饥饿”问题。 因为该算法的不确定性,系统识别效率较低,且仅当标签数目和阅读器给定的时隙数目一致时系统的识别效率平均值可达最大36.8%［1］。

1 问题描述

1.1 动态帧时隙ALOHA 算法

在帧时隙ALOHA(FSA)算法中,当隙数和标签数相等时,可得到系统的最大吞吐量36.8%,在实际中,标签中存储数据的寄存器占8 位,因此标签的ID 的范围为1～256 之间(十进制)。 而实验测试结果发现,当帧时隙取值为256 时系统已经达最大吞吐率。 在实际操作的过程中,在捕获效应和环境噪声等各种因素的影响下,标签的吞吐量常常无法达到最大值。 因此,在FSA 算法的基础上提出了动态帧时隙ALOHA(DFSA)算法。

DFSA 算法的步骤：阅读器通过标签估计算法估计其阅读范围内的标签数目n,设定一个帧长为L的帧时隙,并发送查询指令至标签,标签在接受指令后随即产生一个在1～L 范围内的随机数,并在该随机数对应的时隙时刻响应。 若出现了碰撞,则阅读器让碰撞的标签停止发送数据,等待下一帧的时隙安排。 该帧识别结束,重新进行估计标签估计,调整帧长,进行下一帧的识别［2］。

DFSA 算法可以根据标签数量动态调整帧长,较好地适应系统变化,然而最大吞吐率到达的一个条件为标签数和帧长一致。 但实际操作中,无法准确的得知标签总数,标签数量不能直接提供给阅读器,导致系统的吞吐率无法得到最大值,所以如何估计标签算法成为DFSA 算法中的一个重要的研究方向［3］。

标签估计算法往往使用于每次碰撞之后,估计剩下的标签数量,即标签估计算法一般是基于上一帧的碰撞情况,从而估计标签总数或者下一帧的帧长设定。

1.2 系统吞吐率

设阅读器的帧长为L,阅读器作用范围内的标签总数为n,当任一时隙中有r 个标签,其概率服从二项分布定理,且某个标签处于帧内任一时隙的概率为：

空时隙的发生概率为：

成功时隙的发生概率为：

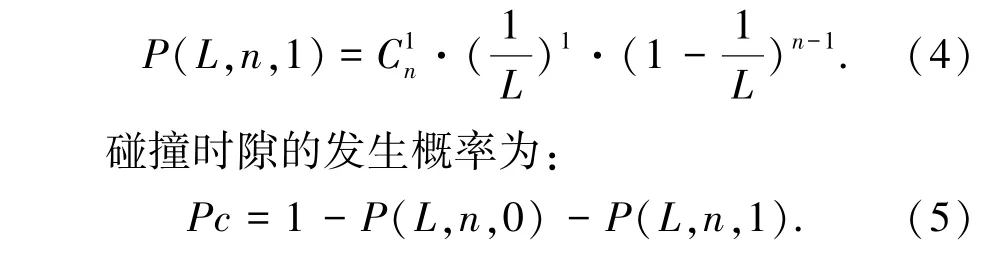
动态帧时隙ALOHA 算法的吞吐率函数表达式(不考虑通信干扰的情况)为：

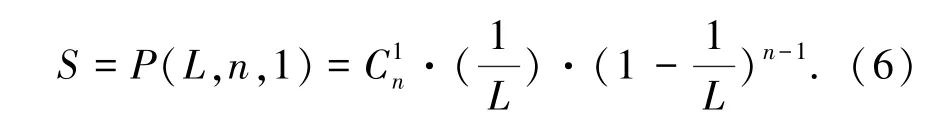
式(6)对n 求导后,可得出最优帧的大小为L =n ＋1,而再代入(5)式中,可知道系统的最大吞吐率稳定在36.8%［4］。

1.3 常用标签估计算法

系统的吞吐率主要取决于标签个数的估计以及帧长的调整,特别是标签总数的估计。 目前有几种主要的标签估计算法：

(1)最小值估计算法。 某一时隙发生碰撞时至少有两个标签,因为设置为未识别标签数至少为碰撞数目的两倍。 该估计算法简单,但当标签数量较大时,其误差率较大。

(2)Schoute 算法。 在最小值标签估计算法的基础上改进,因标签识别过程中整体服从泊松分布,计算得知各碰撞时隙平均响应的标签个数约为2.39,可以预测未识别标签的个数为2.39 乘碰撞时隙数目。 该算法比最小值估计算法更加精确。

(3)Vogt 法。 利用切比雪夫不等式法估计标签数量,根据理论成功、空闲、碰撞时隙与实际时隙对比,找出最小误差结果,从而估计标签数量。 该算法适用于标签动态增加,精确度较高,但其计算复杂度也较高。

(4)伪贝叶斯法。 将阅读器前一次的碰撞、空闲、成功时隙数作为一个先验分布,从此求出标签的一个概率分布函数,通过数学期望来估计标签数目。

(5)生日悖论标签估计法。 利用同一天生日的概率问题对应发生碰撞的概率,计算出成功识别的概率和碰撞概率,从而估计标签总数。

(6)Khandelwal 标签估计法。 通过空闲时隙所占总时隙的概率估算标签的总数量,当空闲时隙增加时,动态地估计标签的数量。

(7)Tag Estimation Method I 法。 利用碰撞率(碰撞时隙数与帧长的比值)估算标签总数。

(8)最小均方差法。 该算法使用切比雪夫定理和最小均方差相结合的方法来估计标签数量。 根据切比雪夫定理可知,每个标签识别周期结束时,已识别标签数和标签总数之比会收敛到一个值。

2 标签估计算法

在DFSA 算法中,当帧长等于待识别标签个数时,理论上可以得到最大的系统吞吐率。 通过对前面几种不同的标签估计算法的比较和研究,多种数学规则和概率原则已经应用了许多,本文给出一种研究时隙比例的思想,大致估算标签总数。

2.1 本文思想

本文算法思想为：理想中成功时隙与空闲时隙的比例对应实际成功时隙与空闲时隙的比例,从而计算出标签总数。

已知(3)式为某个时隙没有标签的概率,则某帧长内空闲时隙数目的数学期望为公式(3)乘上帧长。 同理可得某帧长内成功时隙数目的数学期望。

可得公式(7)为某帧长内空闲时隙数目的数学期望：

由公式(9)可以看出当中含有标签总数和帧长,因而可以利用实际中的成功时隙和空闲时隙的比例,通过该比例计算出标签总数。 但由于实际中一次碰撞出现的成功时隙和空闲时隙的结果有不确定性,如果使用该公式,需要具备一定的数据基础。

通过对公式(6)求导, 得出最优帧长为n ＋1,即L = n ＋1 ,对比公式(9),可知：当系统达到最佳吞吐率时,帧长L =n ＋1,成功时隙和空闲时隙的比值为1,即成功时隙与空闲时隙相等。

因此可以得出结论：即得到最佳吞吐率时,理论空闲时隙数目与成功时隙数目相等。 可以利用成功时隙与空闲时隙的比例来判断标签总数是否大于帧长,当标签总数大于256 最大帧长时,可以进行标签分组。 由于碰撞出现的空闲时隙和成功时隙的结果不稳定,所以只能通过比例是否明显大于1 来判定标签总数和帧长的关系。

2.2 算法过程

(1)阅读器设定一个帧长,并发出识别命令。

(2)标签响应,并返回预定时隙。

(3)阅读器通过对比成功时隙及空闲时隙的比例关系,确定是否分组。 若成功时隙和空闲时隙的比值远远大于1,则得出标签总数大于帧长,需要更改帧长或者进行分组算法进行识别,转(4),否则转(5)。

(4)使用分组算法,分组后阅读器重新设定帧长并发出多次识别命令,收集多次返回的预定时隙结果,取得均值后求出该帧长内的标签总数,转(6)。

(5)阅读器发出多次识别命令,收集标签返回的时隙预定结果,求出该帧长内的标签总数,转(6)。

(6)进行第一次识别,识别后下一帧,帧长设定为标签总数减去上一帧的成功时隙数。

3 仿真验证

本文使用随机数据对本文算法进行仿真验证,对本文算法和其他算法做一个对比。

3.1 仿真环境

本文算法代码使用MATLAB 语言实现,硬件环境是8 核Intel i5 处理器,内存为8GB,硬盘为1TB的笔记本,底层操作系统为Windows 10。

3.2 仿真数据

本文算法使用随机数据,使用MATLAB 内部函数生成随机数,仿真的标签总数由1 到300。

3.3 对比算法介绍

在Schoute 标签估算算法中,所有标签在一帧内符合λ = 1 的泊松分布,则每个碰撞时隙中平均有2.39 个标签,因此当标签数等于帧长的情况下得到L=n=2.39*C,C 为上一帧碰撞总数。 这个结果是在最大系统效率前提下得出的,该方法精度不高,但是算法相对简单［5］。

3.4 仿真情况

对本文想法做了一次碰撞之后的仿真,运用MATLAB 对第一次碰撞结果仿真标签总数由1 到300,同时找了y=x 线性方程作为标准线,图1 为仿真结果。

图1 拟合对比图Fig. 1 Matching comparison

由图1 可看出本想法与实际的标签量走势一致,但是结果极不稳定,这是因为标签实际碰撞得出的空闲时隙和成功时隙的结果不稳定,而本文想法为理想的碰撞结果,因此需要大量的数据基础。

进行了100 次本文算法的仿真并取平均值后,得到了图2,作为对比,这里加上了一次函数与Schoute 算法作为对比。

由图2 的结果可以看出当实验100 次后,本文方法能够很好的拟合出标签总数,甚至要比Schoute算法更加贴近标准线y = x。

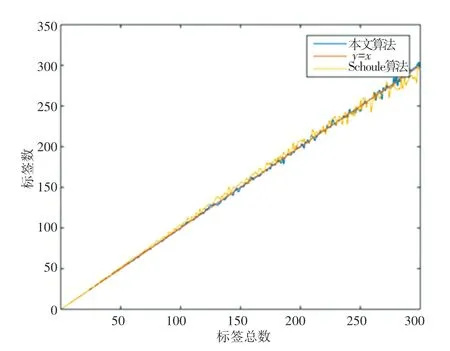
图2 100 次数据基础下的拟合对比图Fig. 2 Matching comparison chart based on 100 times data

当帧长为180 时,随着标签数量的增加,成功时隙／空闲时隙的比例,结果如图3 所示。

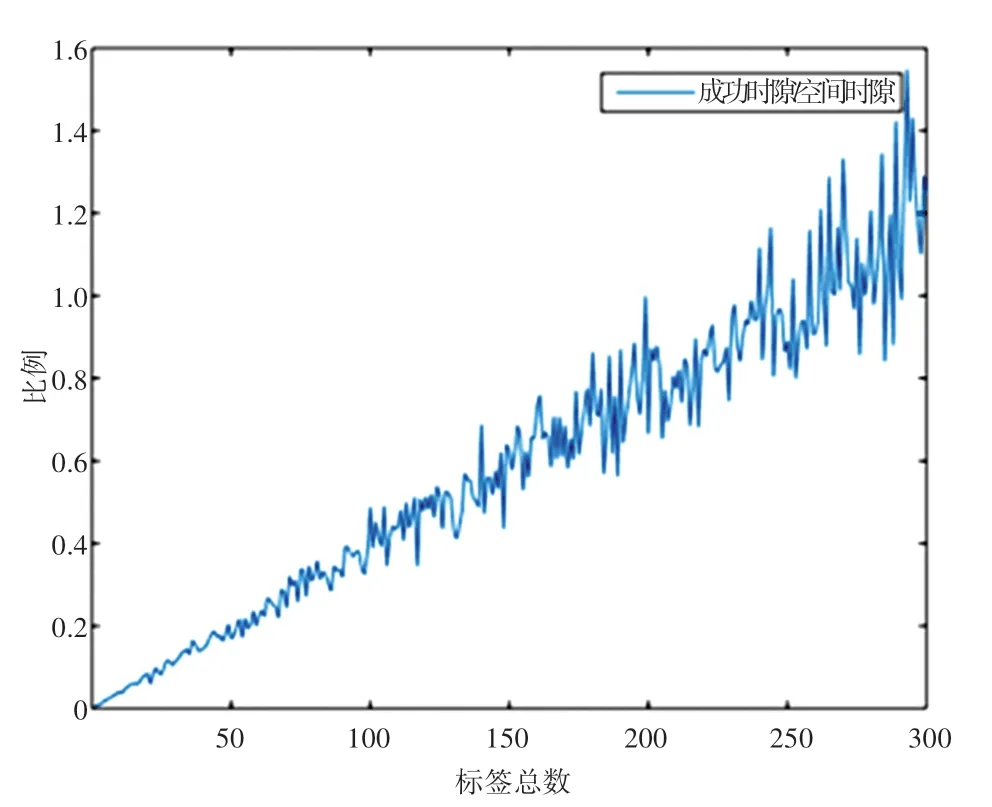
图3 成功时隙／空闲时隙随标签总数变化Fig. 3 Change of successful time slot ／ idle time slot with the total number of tags

由图3 可以看出,随着标签数量的增加,成功时隙／空闲时隙的比值越来越大,而在150 到180 左右达到1,即当标签总数小于帧长时,成功时隙小于空闲时隙；而当标签总数大于帧长时,成功时隙大于空闲时隙；当标签总数与帧长相等时,空闲时隙与成功时隙相等。

4 结束语

(1)适用于分组算法,利用第一次碰撞时出现的空闲时隙和成功时隙的比例,判断标签总数与帧长的关系。 当成功时隙大于空闲时隙,即成功时隙／空闲时隙＞1 时,标签总数大于帧长；当成功时隙小于空闲时隙,即成功时隙／空闲时隙＜1 时,标签总数小于帧长。

算法具体实施方法：首次识别,设定一个帧长,通过识别后得到碰撞结果,得出成功时隙和空闲时隙的比例,判断标签总数与帧长的关系,若成功时隙和空闲时隙的比值远远大于1,则得出标签总数大于帧长,需要更改帧长或者进行分组算法进行识别。

(2)适用于估计标签总数,识别标签前,模拟100 次碰撞结果,得出成功时隙和空闲时隙的比例,再利用公式(9),计算得出标签总数n。

算法具体实施方法：当阅读器进行识别时,向标签发出多次识别信号,收集多次的成功时隙和空闲时隙的结果,取得均值后求得标签总数。 进行识别,帧长设定为最开始的标签总数减成功时隙。本文算法的缺点：

误差较大,一次的成功时隙和空闲时隙的发生情况存在不稳定性,因为用于判断标签总数存在误差,且误差率较大,因而只能运用于大致比较,可使用于确认是否需要使用分组算法。

需要大量的数据基础,因为成功时隙和空闲时隙的不稳定性,因此需要阅读器多次发出识别信号以获得大量的数据基础,从而保证结果稳定。