连续潮流在功率极限附近不收敛问题的研究
2020-11-09高成
高成
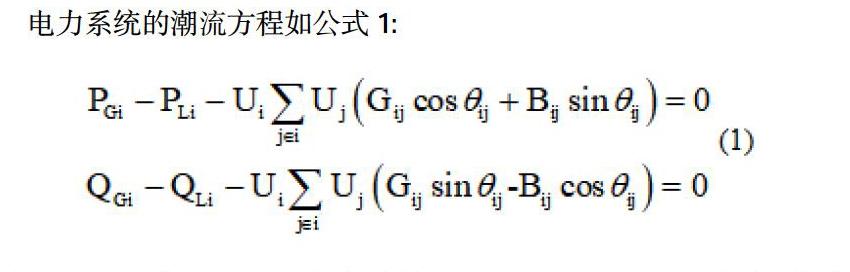
摘要:针对连续潮流计算过程中在功率极限附近不收敛问题,本文提出一种简化的类潮流方程模型来模拟连续潮流求取PV曲线,通过对潮流模型分析计算,得出切线预测由于其自身特性不适合于功率极限附近的连续潮流计算,物理参数化和正交参数化也不适合于在功率极限附近的连续潮流计算等结论。通过实例验证了所研究结论的正确性。
关键词:电力系统分析;连续潮流;PV曲线;潮流方程模型
0引言
2012年7月30日和7月31日,印度电网发生两次由于输电断面的突然开端引发系统崩溃[1]。这次事故给人们带来了巨大的经济损失和严重的社会紊乱,引起电力界的普遍关注。随着我国逐步实现“西电东送、南北互供、全国联网”的战略构想,电力系统电压稳定问题和电压崩溃问题受到越来越大的重视。连续潮流法能够画出电力系统负荷节点的PV曲线,是电力系统电压稳定性和电压崩溃研究的重要方法,其算法的精確度、稳定性以及高效直接关系着电力系统分析的有效性[2]。为了克服常规潮流法在功率极限点处雅克比矩阵奇异的问题,连续潮流通过引入负荷增长因子,并增加一维参数化方程,从选定的己知潮流解开始按照负荷增长的方向,对下一潮流解进行预测、校正,巧妙地解决了潮流雅可比矩阵奇异的难题,从而能够追踪潮流解的轨迹。目前,连续潮流法在预测环节主要有切线预测、割线预测、拉格朗日预测、牛顿插值预测等[3];在具体的连续潮流计算中这些方法都需要进一步的研究。
针对在连续潮流计算过程中在功率极限附近数值震荡问题,文献[4]提出采用潮流多解进行改进,这种方法只是在牺牲精度的条件下避免了数值震荡问题。针对在连续潮流计算过程中在功率极限附近发散问题,文献[5]提出采用弧长参数法进行改进,此法改进了参数化环节潮流发散问题,可是没有考虑预测估计环节的问题。另外,文献[6]论证了潮流不收敛是由于连续潮流法在功率极限附近对负荷参数的过度依赖。连续潮流法由于其在计算的过程中受电力系统参数、预测估计方法、校正方法等因素的影响仍存在潮流不收敛的问题,不能有效地求出所需功率极限值。因此,对连续潮流发散的原因进行深入探究将十分必要。
本文在了解电力系统潮流计算的机理以及连续潮流法原理的基础上,针对连续潮流在功率极限附近仍存在不收敛和数值震荡问题,利用类潮流方程的非线性一元二次方程来模拟连续潮流求取PV曲线,进而对连续潮流各个环节的特性以及导致潮流计算发散的原因进行探究。并通过实例验证了所研究结论的正确性。
1.潮流方程模型
电力系统的潮流方程如公式1:
(1)
式中:、为节点i发电机发出的有功和无功,、为节点i负荷消耗的有功和无功,、为节点i的电压,为节点j的电压,、为电力系统导纳矩阵的电导和电纳,为节点i和节点j的相位差。在实际输电系统中,根据有功功率与两端电压相位差之间,无功功率与电压损耗之间呈比较紧密的关系[7],可以理解为在无功潮流方程中,两节点的相角查为常数,节点电压和节点无功呈二次关系。那么,电力系统的潮流方程是一组多维高度耦合的拟二次非线性方程,基于该思想,提出利用一个简单的一元二次非线性方程来模拟潮流方程,利用连续潮流法对其轨迹进行追踪绘制,以分析实际连续潮流绘制时潮流不收敛的原因。潮流方程模型如公式2,
(2)
式中:x为节点负荷功率,y为节点电压,参数a一般取相应节点额定电压的一半,参数b一般取相应节点的功率极限。
一般地,电力系统工作者和研究人员采用IEEE标准测试系统数据进行电力系统各类算法进行研究,IEEE标准数据有IEEE-14、IEEE-30、IEEE57、IEEE118和IEEE300五套,这些系统对于连续潮流算法的研究分析还是比较复杂的。采用更加简单的电力系统,如夏道止主编的《电力系统分析》第二版第四章的简单闭式网络4节点的电力系统,就会产生有九个非线性方程的潮流方程组,也会增加连续潮流算法研究的复杂性。选取公式2的潮流方程模型,简化连续潮流的计算,易于分析连续潮流在功率极限附近不收敛的原因。
2. 基于潮流方程模型的研究
连续潮流在功率极限附近不收敛主要有两个原因,其一,预估值不准确,由于连续潮流对负荷的依赖性造成连续潮流出现数值震荡现象;其二,扩展潮流方程无解,由于连续潮流参数化方程和潮流方程无解造成的连续潮流发散问题。
2.1 针对功率极限附近数值震荡问题
首先,使用夏道止主编的《电力系统分析》第二版第四章的简单闭式网络4节点电力系统进行研究,采用纯切线预测,步长设置为0.05,采用正交参数化和牛顿法进行校正,结果在计算第28个潮流解时发散,潮流解跳出有效范围。
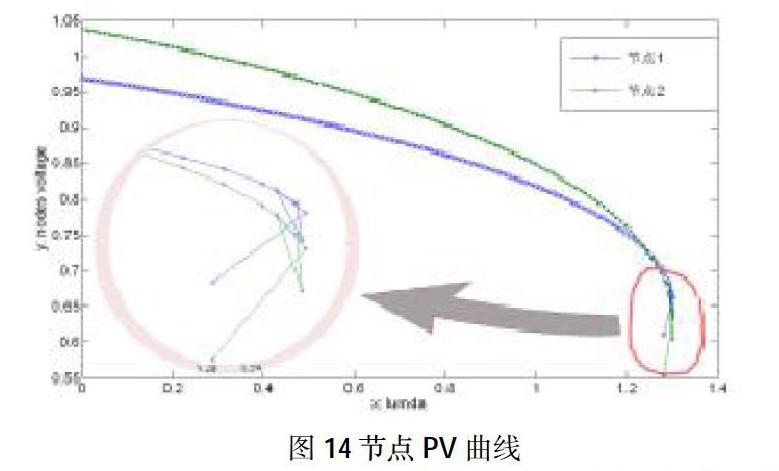
减小步长如图1所示,步长设置为0.01,计算潮流解135个时潮流开始出现震荡发散;当进一步减小步长,则在负荷极限附近出现震荡现象(如图1放大部分所示)。
由于系统方程比较复杂,不利于分析,现采用潮流方程模型进行模拟计算。如图2所示,设置参数a取0.5,b取1.5, 对其采用相同的切线预测、正交参数化和牛顿法校正。结果依然在极限点附近出现震荡现象。
分析其原因是由于切线预测对负荷增长方向的依赖性导致的,当潮流解已经越过极限点时,由于不能够得到及时有效的判断(负荷虽然一直在增大,但潮流解已经越过极限点),连续潮流朝着反向进行预估校正,这样形成震荡,甚至是发散。由于潮流方程模型的简化结构,潮流可以很好的收敛。在实际的复杂电力系统中,潮流将会经常出现发散,而且难于分析其原因。因此,切线预测在极限点附近震荡的原因是由于切线预测本身特性所导致。为了绘制完整的PV曲线,必须使用其他的预测方法
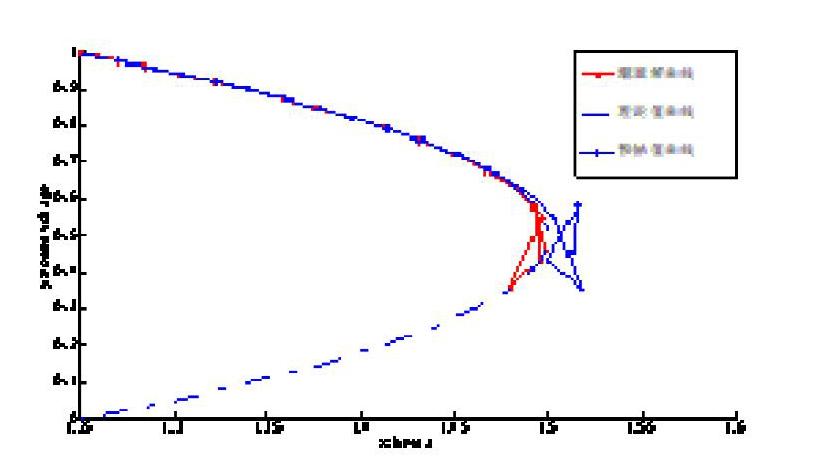
切线预测估计法虽然具有自启动能力,即依靠单个初始潮流解进行预估,但是不适合应用于功率极限附近的预测估计。同样的分析方法可知,割线预测、拉格朗日预测和牛顿差值预测都不具有对负荷的依赖性,如图3所示其他条件不变,基于割线预测的潮流解PV曲线。
2.2 针对功率极限附近潮流不收敛问题
另外,在预估值正确的前提下,仍然存在连续潮流在功率极限附近潮流不收敛问题,物理参数化法示意图,当步长选取过大,由于参数化方程和潮流方程没有公共点,所以扩展的潮流方程无解;同理,在正交参数化方法,连续潮流在功率极限附近不收敛。
分析可知,物理參数化法适合于在PV曲线比较平稳的区域进行参数化计算,不适合功率极限附近的连续潮流计算。正交参数化法虽然能够画出功率极限附近的PV曲线,但是由于受到步长的约束限制,当步长选取过大连续潮流会出现发散现象。因此,正交参数化法不适合于编写通用连续潮流程序模块。
3. 总结
综合上述,本文提出了一种新的潮流方程模型,能够简化电力系统潮流方程,通过分析得出连续潮流在功率极限附近不收敛的两类不同情况,为编写通用连续潮流模块和电力系统分析提供理论支持。模型的结果表明,在功率极限点使用切线预测并非系统在该功率点处潮流不收敛,而是切线预测本身特性所致,因此切线预测不适于连续潮流法功率极限附近的潮流计算;另外得出物理参数化和正交参数化不适合于功率极限附近的连续潮流计算的结论。
参考文献
[1]方勇杰, 用紧急控制降低由输电断面开断引发系统崩溃的风险对印度大停电事故的思考. 电力系统自动化, 2013(04): 第1-6页.
[2]王锡凡, 现代电力系统分析. 2003, 北京: 科学出版社.
[3]石洋, 基于GMRES改进连续潮流法的静态电压稳定研究, 2011, 太原理工大学.
[4]周双喜, 冯治鸿与杨宁, 大型电力系统PV曲线的求取. 电网技术, 1996(08).
[5]祝达康与程浩忠, 求取电力系统PV曲线的改进连续潮流法. 电网技术, 1999(4): 第39-42+50页.
[6]蔡伟程与代静, 对求取电力系统PV曲线的连续潮流法的改进. 电力系统及其自动化学报, 2005(5): 第82-85页.
[7]夏道止, 电力系统分析.第 第二版 版. 2004, 北京市: 中国电力出版社.
作者简介:
高 成(1988-),男,四川乐山人,硕士,主要从事电力系统分析研究。
