秸塑复合材料蠕变性能分析*

张思成,盛冬发,董春雷,齐荣庆

(1. 西南林业大学 土木工程学院,昆明 650224;2. 西南林业大学 材料工程学院, 昆明 650224)

0 引 言

世界上的四大基础原材料分别为木质原材料、塑料、钢材和水泥，而其中仅仅只有木质原材料是属于可再生资源。然而，由于人类大规模滥砍滥伐与破坏森林等不文明行为，造成如今木材资源的严重不足[1]。作为木材的替代产品，秸塑复合材料有较好的力学性能、环保性能及可回收再利用性能，业已在各领域得到广泛应用，受到世界各国与相关环保部门高度关注。在实际的农业生产活动中，秸秆的生产量相当惊人，仅每1kg小麦就可以产出1.5 kg的麦秸。而根据联合国环境署(United Nations Environment Programme)相关统计，世界上每年多种粮食农作物所产生的秸秆产量高达18亿吨[2]。中国作为传统的农业大国，在我国农作物主要以小麦、水稻和棉花为主，每年产出的秸秆总量约为7亿吨，其中小麦和水稻秸秆占60%。这些农作物秸秆的年产量巨大，生物纤维含量极其丰富，可作为原材料以替代木质原材料的重要资源[3]。然而我国对农作物秸秆的利用处理方法还相对落后，除了造纸和作为牲畜饲料外，大多数仍是以掩埋或焚烧方法处理，不仅浪费资源同时还造成了环境污染[4]。于是针对我国的这种现状，秸秆的合理有效化利用就成为了迫切的需求。同时由于全球能源短缺与环境气候问题的恶化等有关环境能源问题的严峻趋势，利用可再生的生物资源以用来制造新型复合材料，就愈发引起了人们的高度重视[5]。

秸塑复合材料(SPC)是以植物纤维为主要成分，并通过与热塑性塑料混合，选用合理的加工成型方法复合而形成的一种新型复合材料[6]，具有生物降解性与可再生性，可应用于高温、长期荷载等工作环境中，在环境保护和节约资源方等面均具有重要的意义。随着现代科学研究的深入发展，秸秆基础质原料分子聚合物即秸塑复合材料已经被研制生产出来[7]。秸塑复合材料可以充分利用废旧麦秸秆与废旧塑料实现了废弃物的循环利用，达到环保的目的，因此被世界上许多国家列为新型环保节能绿色产品[8]。秸塑复合材料作为一种新型复合材料，其产品在美国、英国、法国、日本等国家的各行业特别是建筑行业简到广泛应用，而在我国的应用还有待于提高[9]。随着秸塑复合材料的广泛应用，其静动态蠕变特性已成为工程界一项重要课题，引起材料和力学研究人员极大兴趣。美国材料实验协会(American Society of Testing Materials)出台了秸塑复合材料的相关标准[10-12]。然而，国内对秸塑复合材料的研究大都侧重在材料制备方法上，而对于其材料静动态蠕变特性的研究相对较少，关于秸塑复合材料的相关标准仍未见报道[13-15]。

由于秸塑复合材料中植物纤维是与塑料相互黏结，而绝大多数塑料的性能受温度影响较大，因此研究秸塑复合材料的蠕变特性随温度变化的关系显得十分重要[16]。此外，秸塑复合材料的蠕变过程应是应力以及环境温度共同作用的结果。随着应力的递增秸塑复合材料的蠕变力学性能会出现显著变化，因而在研究秸塑复合材料静动态蠕变属性时必须顾及应力的影响因素[17]。

本文研讨秸塑复合材料在等温不同应力下和等应力不同温度下的短期蠕变行为。首先，进行了等温不同应力下以及等应力不同温度下的蠕变试验，取得等温不同应力以及等应力不同温度前提下的蠕变柔量与时间的关系曲线。利用时间-温度-应力等效原理分析了秸塑复合材料的非线性蠕变行为，分别得到了在参考应力水平下与参考温度下的蠕变主曲线，并利用Burgers力学模型进行拟合，得到了秸塑复合材料的蠕变柔量函数表达式。充分利用WLF表达式，通过秸塑复合材料在高温高应力前提下的蠕变柔量推导了该材料在低温低应力前提下的蠕变柔量，从而可以通过在较高温度或较高应力水平下的短时间蠕变行为来预测在低温或较低应力水平下材料的长时间蠕变行为。

1 蠕变模型及时间温度应力等效原理

能将一个Kelvin分析模型和一个Maxwell分析模型串连起来即可获得秸塑复合材料的Burgers蠕变力学分析模型[18]如图1所示。

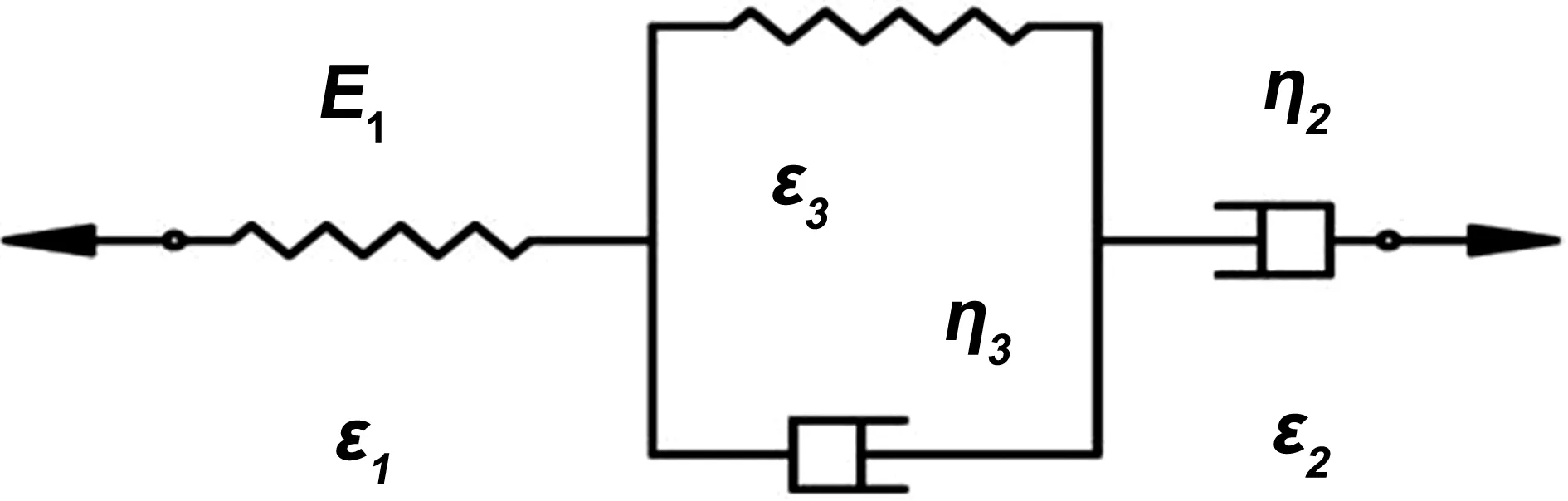
图1 秸塑复合材料Burgers蠕变模型

该模型的应力σ和应变ε可用元件参量表示为

(1)

式中ε1为弹性变形，ε2为黏性变形，ε3为黏弹性变形，E1为瞬时弹性模量，E3为延时弹性模量，η2为黏性系数，η3为黏弹性系数。再由Laplace变换与逆变换可导出该力学模型的本构关系为

(2)

对该力学模型的本构方程(2)进行Laplace变换与逆变换，则可推导出秸塑复合材料的蠕变过程的表达式为

(3)

并令

(4)

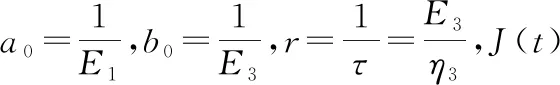
时间-温度-应力等效原理[19]认为黏弹性建筑材料在不同时间尺度上的力学行为可以通过改变环境温度来促成，其实质在于建筑材料黏弹性松弛时间的环境温度相关性，并且应力前提同温度前提条件具备等效性。根据此原理能够将不同环境实验温度或不同应力下的蠕变曲线进行平行移位，从而形成在参考温度或参考应力下的蠕变主曲线，进而通过材料在较高温度或较大应力前提下的短期蠕变行为来预测材料在较低应力前提水平或较低温度前提下的长期蠕变行为。在该理论中，有著名的WLF(Williams-Landel-Ferry)方程[20]即

(5)

式中ασ为应力移位因子，αT为温度移位因子，C1、C2、D1、D2均为材料常数，σ为应力，σ0为参考应力，T为温度，T0为参考温度。需要说明的是，本文所求解的秸塑复合材料的WLF方程的适用温度范围为10～160 ℃。

2 实 验

实验仪器采用深圳三思纵横科技股份有限公司生产的新型微机控制电子式蠕变持久试验机。实验原料选用德州临邑无畏同创农业科技有限公司生产的小麦秸秆粉(60目筛)以及杭州长惠进出口公司生产的HDPE回收废弃塑料。将秸秆粉经干燥处理后，按照与HDPE回收废弃塑料所占配料比约为70∶30进行混合，再加入粘合剂采用热压工艺进行制备，将所制备的秸塑复合材料通过制样机加工后即得到实验所用试件，且试件尺寸为100 mm×15 mm×15 mm。将试件分成数量相等的两批试件，同时进行预处理即将两批试件置于恒温恒湿箱中密闭加热至90 ℃，然后恒温2 h后取出，在室温的条件下静置冷却36 h，这样预处理保证了两批试件处于同一初始状态。

等温度不同应力下的蠕变实验，将第一批试件进行预处理后加热至85 ℃，再以1 ℃/min的冷却速率冷却至测试温度60 ℃，然后将试件保持恒温60 min，再分别进行在1.5、3、4.5和6 MPa的恒拉应力作用下蠕变实验。将实验取得的原始数据转换演变成蠕变柔量的方式，则取得等温度各异应力下的蠕变实验曲线，并均以t×103s取对数作为横坐标的值，例如见图2所示。从图2中可以反映出随着应力的增大时，秸塑复合材料的蠕变柔量也随之增大，此时该蠕变曲线反应了秸塑复合材料的非线性黏弹性。

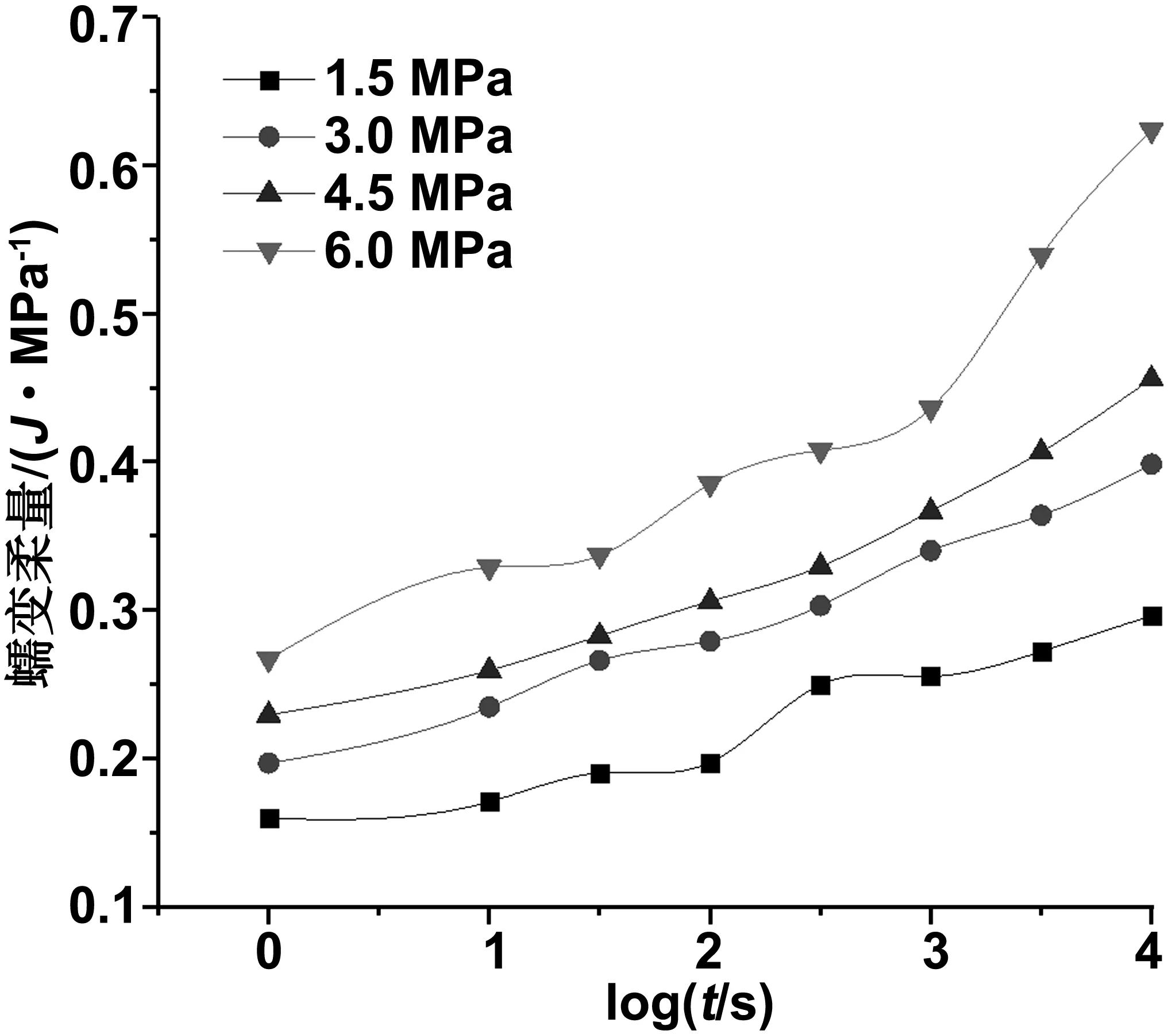
图2 等温度不同拉应力下的蠕变柔量曲线

等拉应力不同温度下的蠕变实验，将第二批试件进行预处理后加热至85 ℃，再以1 ℃/min的冷却速率分别冷却至测试温度60、50、40、30和20 ℃，然后将试件保持恒温60 min，再进行在6 MPa恒拉应力作用下蠕变实验。将实验所得数据转换成为蠕变柔量的形式，则得到等应力不同温度下的蠕变实验曲线，并均以t×103s取对数作为横坐标的值，如图3所示。从图3中可以很容易看出秸塑复合材料的蠕变性能受温度影响较为显著，当实验温度升高时该材料的蠕变柔量随之增大。

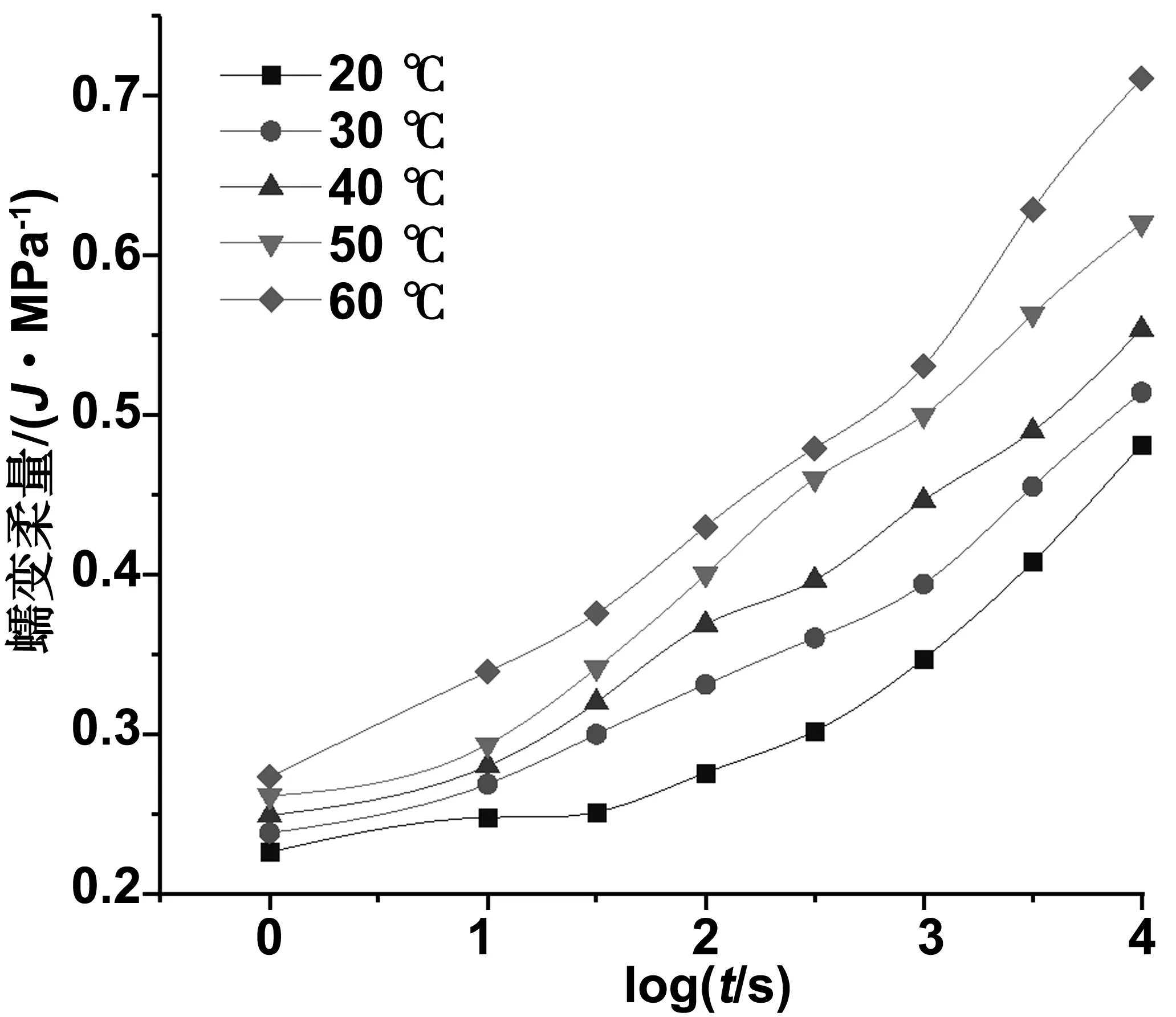
图3 等应力不同温度下的蠕变柔量曲线

3 结果与讨论

3.1 等温度不同应力蠕变性能分析

以图2中的1.5 MPa拉应力为参考应力，将图2中其他应力技术水平的蠕变曲线进行相应的水平移位，即可获得秸塑复合材料的蠕变柔量主曲线，例如见图4所示。

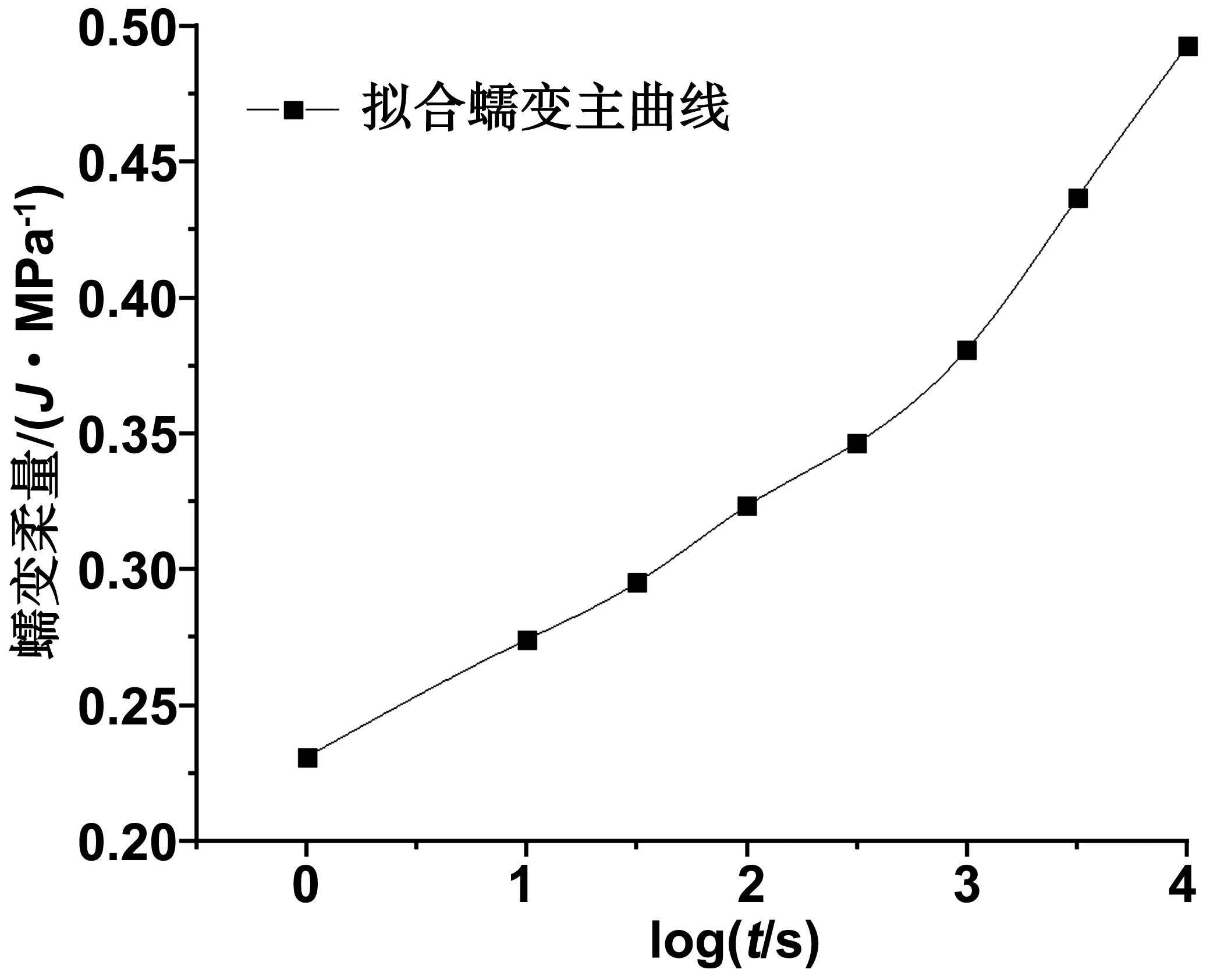
图4 蠕变柔量主曲线

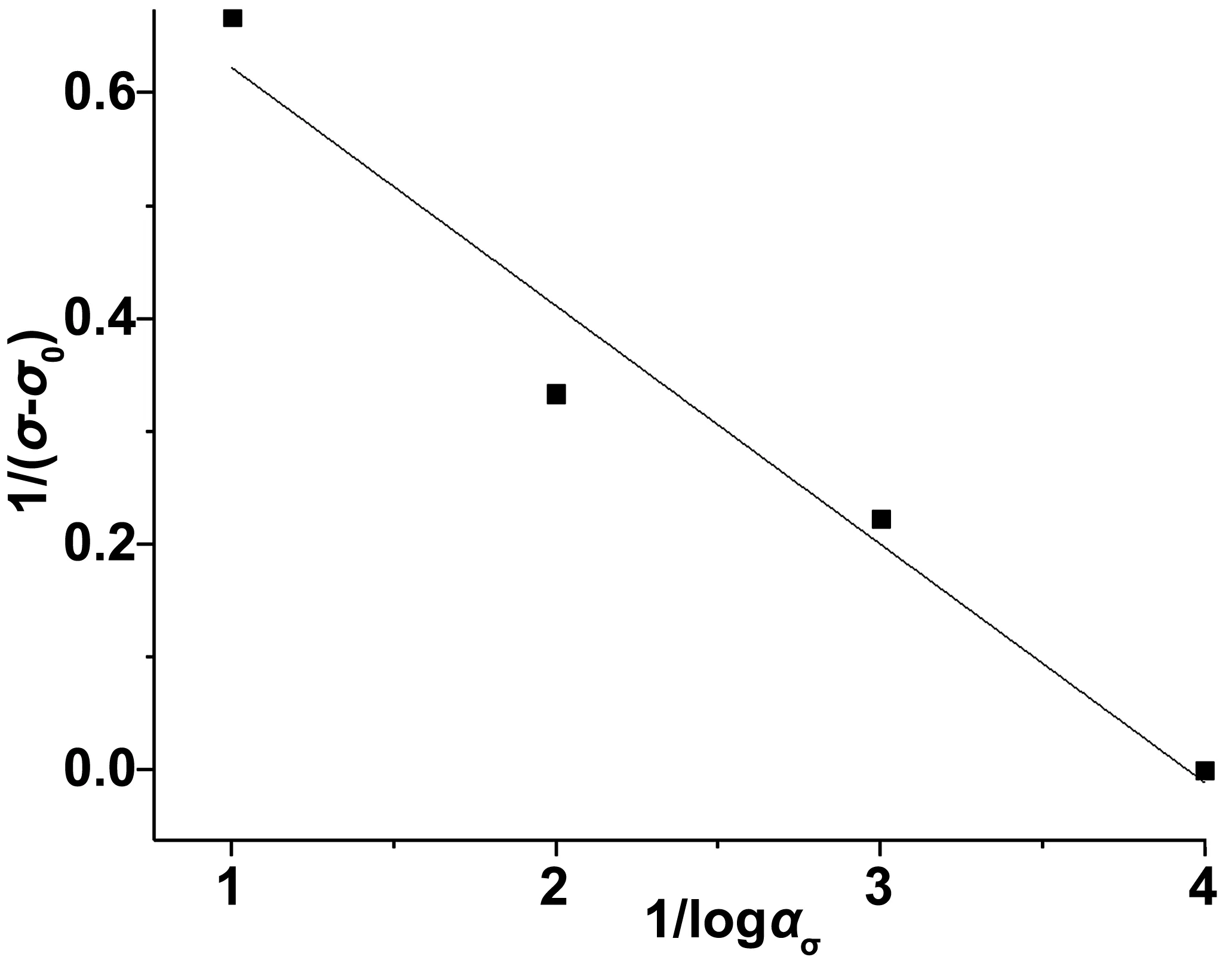
图5 应力移位因子与应力的关系

在平行位移的过程中，可得到相应的应力移位因子ασ，据此得出应力移位因子ασ与应力σ-σ0之间的关系如图5所示。对式(5)进行非线性回归拟合，则可得到材料常数C1=0.253、C2=-1.2 MPa。从而秸塑复合材料的WLF方程即为

(6)

接着将图4中的蠕变柔量主曲线利用Burgers蠕变分析模型即等式(4)展开拟合，能求得该类分析模型中的待定参数值，例如从表1所示

表1 Burgers蠕变模型拟合参数

从而秸塑复合材料的蠕变柔量函数表达式为

J(t)=0.231+0.261(1-e-0.0278t)+1.128×10-8t

(当σ0=1.5 MPa时)

(7)

在表1中，Burgers蠕变分析模型的拟合相关系数为0.98557，说明该类力学模型的拟合准确度中较高，通过该类力学模型取得的蠕变柔量理论值与实验数值极其趋近。对于等温度不同应力的其他曲线，同样利用时间-温度-应力等效原理分别以3、4.5和6MPa为参考应力进行平行移位得到蠕变主曲线再同样利用Burgers蠕变模型进行拟合，则可分别得到三种参考应力条件下的蠕变柔量函数表达式，即

J(t)=0.244+0.298(1-e-0.0334t)+1.576×10-8t

(当σ0=3 MPa时)

J(t)=0.253+0.316(1-e-0.0471t)+1.739×10-8t

(当σ0=4.5 MPa时)

J(t)=0.276+0.439(1-e-0.0562t)+1.896×10-8t

(当σ0=6 MPa时)

(8)

需要说明的是，限于篇幅，这里不再赘述其他3种参考应力条件下的蠕变主曲线。从式(7)和式(8)很容易看出秸塑复合材料的蠕变柔量函数受参考应力变化的影响，当增大应力时该材料的蠕变柔量随之增大。该理论结果与实验结果进行比较，容易发现理论与试验结果接近。

3.2 等应力不同温度蠕变性能分析

以图3中的60 ℃为参考温度，其它应力的蠕变曲线进行相应地水平移位，即可得到秸塑复合材料的蠕变柔量主曲线如图6所示。

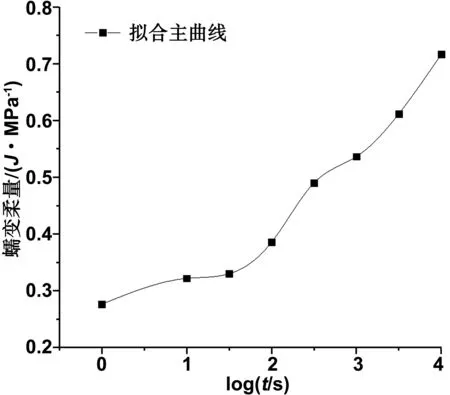
图6 蠕变柔量主曲线

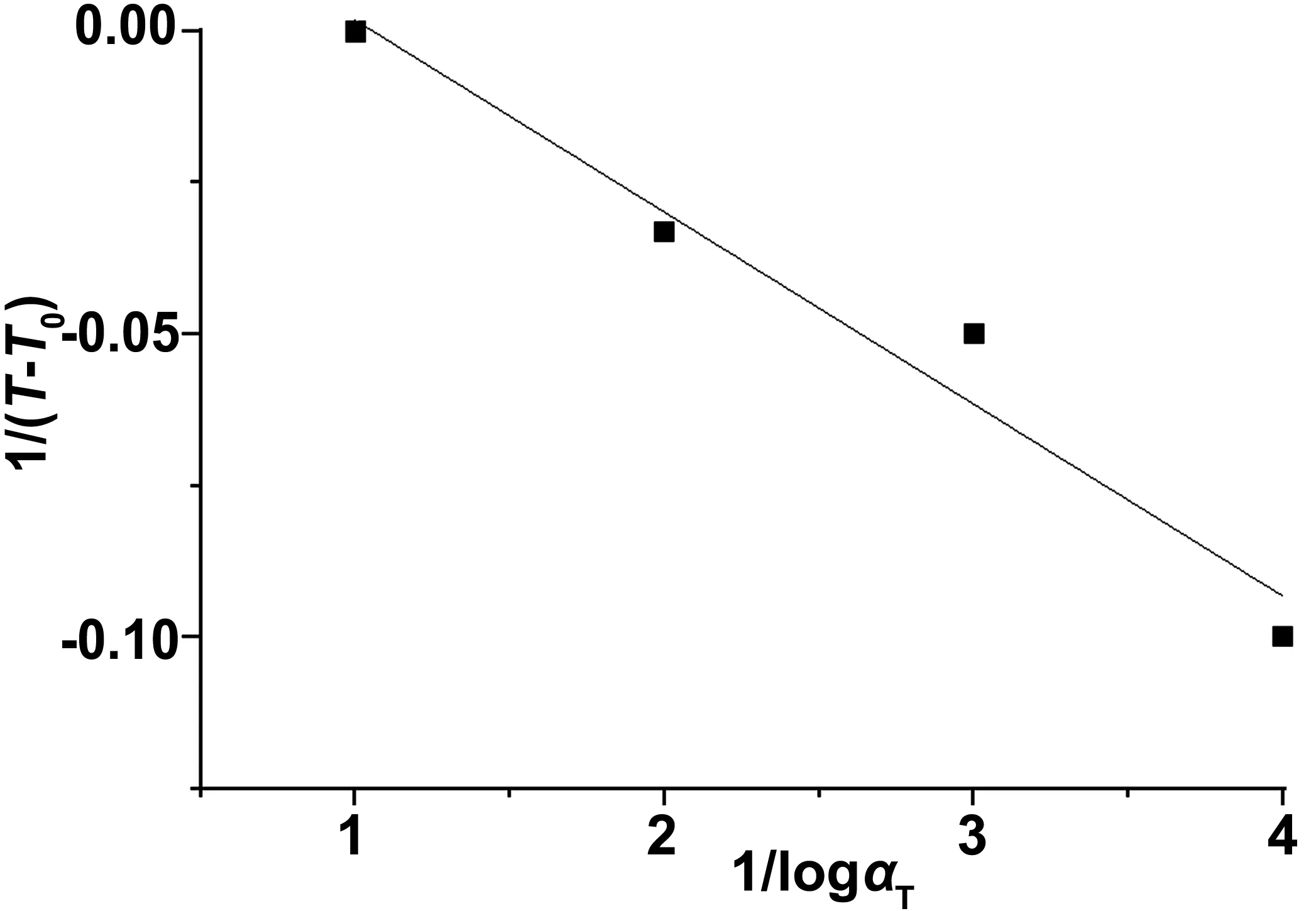
图7 时温移位因子与温度的关系

并且在平行位移的过程中，可得到对应的温度移位因子αT。据此得到温度移位因子αT与温度T-T0之间的关系如图7所示。对式(5)进行非线性回归拟合，则可得到材料常数D1=0.946、D2=-29.851 ℃。从而秸塑复合材料的WLF方程可写为

(9)

对于图6中的蠕变主曲线，可利用Burgers蠕变分析模型，即等式(4)进行拟合，可得该类分析模型中的待定参数值，如表2所示。

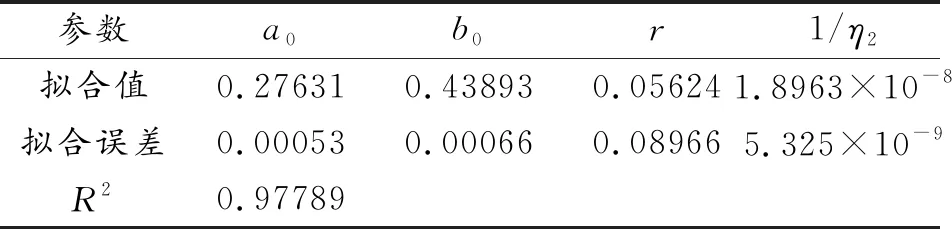
表2 Burgers蠕变模型拟合参数

从而秸塑复合材料的蠕变柔量函数表达式为

J(t)=0.276+0.439(1-e-0.0562t)+1.896×10-8t

(当T0=60 ℃时)

(10)

在表2中，Burgers蠕变模型的拟合相关系数R2为0.97789，说明该模型的拟合精度较高。通过此力学模型得到的蠕变柔量理论值与实验值较为接近，可为秸塑复合材料的蠕变性能分析提供一定参考依据。对于等应力不同温度的其余曲线，同样利用时间-温度-应力等效原理分别以50、40、30、20 ℃为参考温度进行平行移位得到蠕变主曲线，再利用Burgers蠕变模型进行拟合，则可得到四种不同参考温度条件下的蠕变柔量函数表达式即

J(t)=0.261+0.357(1-e-0.0483t)+1.773×10-8t

(当T0=50 ℃时)

J(t)=0.249+0.306(1-e-0.0369t)+1.614×10-8t

(当T0=40 ℃时)

J(t)=0.238+0.276(1-e-0.0297t)+1.225×10-8t

(当T0=30 ℃时)

J(t)=0.226+0.255(1-e-0.0236t)+1.116×10-8t

(当T0=20 ℃时)

(11)

需要说明的是，限于篇幅，这里也不赘述其他参考温度条件下的蠕变主曲线。从式(10)、式(11)可以看出秸塑复合材料的蠕变柔量受温度变化的影响较为明显，当温度升高时该材料的蠕变柔量随之增大。将理论与实验结果进行比较，发现理论与实验得到的结果相近。

最后，可借助求解出的秸塑复合材料的时间-温度-应力的等效原理中的WLF方程即式(6)或式(9)，经由该材料在较高温度或较高应力前提下的短时间蠕变行为来预测材料在低温或较低应力水平前提下的长时间蠕变行为。下面利用高温与高应力前提下的短时间蠕变行为，简述预测对秸塑复合材料在低温或较低应力水平前提下长时间蠕变行为的推导过程。以式(6)中得到的参考应力1.5 MPa下的应力移位因子为

J(t)=0.132+0.211(1-e-0.0137t)+0.783×10-8t

(12)

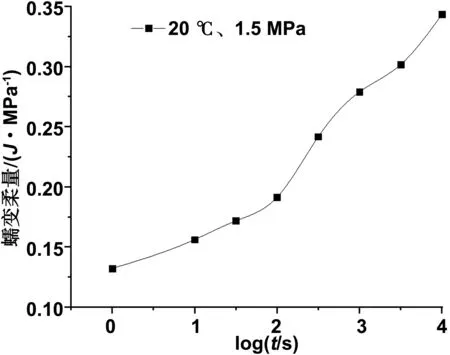
图8 20 ℃、1.5 MPa时的蠕变柔量主曲线

已知条件，将式(11)中当T0=20 ℃时的蠕变柔量函数即进行平行移位，得到在参考应力1.5 MPa，温度为20 ℃条件下的蠕变主曲线如图8所示。此时秸塑复合材料的蠕变柔量函数为经过上面的分析探讨，表明借助秸塑复合材料的时间-温度-应力等效性原理中的WLF公式方程，我们可以通过秸塑复合材料在高温或高应力水平前提下的短期蠕变行为来预测该类原材料在低温或低应力前提下的长期蠕变行为。

4 结 论

(1)进行了秸塑复合材料在等温不同拉应力与等拉应力不同温度下的蠕变实验，利用Burgers力学模型与时间-温度-应力等效性原理中的WLF方程，拟合得到秸塑复合材料的蠕变表达式，通过原材料在高温高应力前提条件下的蠕变柔量推导了秸塑复合材料在低温低应力条件下的蠕变柔量，与实验结果进行对比验证，证明本文理论可有效地推导该类材料在低温低应力条件下的蠕变柔量。

(2)环境温度与应力对秸塑复合材料的蠕变性能影响显著。随着环境温度的升高或应力的递增，秸塑复合材料的蠕变柔量均随之增大。

(3)由于Burgers力学模型的拟合精度为0.98857与0.97789，该模型拟合度较高，说明Burgers力学模型可较好地拟合秸塑复合材料的蠕变柔量主曲线。