基于Argo剖面和SST以及SLA数据重构三维网格温度场

李直龙，左军成，纪棋严，罗凤云，庄圆

（浙江海洋大学，浙江舟山316022）

1 引言

利用辐射计和高度计等各种卫星传感器，可以获取大量的海洋表面信息，包括海表温度（Sea Surface Temperature，SST）和 海 表 面 高 度（Sea Surface Height，SSH）等。虽然卫星遥感观测数据具有覆盖面积大、精度高、时间和空间分辨率高的特征，但仅通过它们无法获得海洋表面以下的信息用于研究海洋内部结构和变化规律。海洋垂向的观测资料主要来源于船只走航、站点观测、潜标、水下滑翔机和浮标等，其中以实时地转海洋学漂流浮标阵列（Array for Real - time Geostrophic Oceanography，Argo)获取的观测资料最多。基于Argo 项目建立了一个实时全球海洋观测系统，针对2000 m 米以上的海洋进行采样，获取能覆盖全球的温度和盐度剖面资料。自1998 年以来Argo 项目共收集了180 多万份剖面资料。虽然Argo 剖面资料的覆盖范围和数量都远远超过了之前的传统观测结果，但是在时间和空间上的分辨率仍然存在不足。为了研究三维海洋，利用SST 和SSH 数据，结合Argo 剖面数据重构高分辨的三维温度和盐度场已经成为一个重要的研究课题。

自20 世纪80 年代以来，海洋学家已经提出了多种方法利用海表信息重构三维温度和盐度场[1-5]，包括物理方法、海洋模型同化技术和统计方法。Hurlburt[6]通过考虑水动力和能量交换的特征，建立海洋数值模型，将高度计数据动态传递到海洋下层。Chu 等[7-8]开发了一个热参数模型，根据温度场的分层结构来分析观测区域的海温曲线，获取每个海温曲线的混合层深度（Mixed Layer Depth，MLD）、温跃层深度和温跃层温度梯度等特征。Yan等[9]提出了一种基于三维变分（Three Dimensional VARiational，3DVAR）分析的数据同化方案，根据海面动力高度信息估算下层温盐剖面，并考虑了温度和盐度背景误差的垂直相关性以及非线性T-S 关系。王喜冬等[10]采用回归分析方法，利用历史温盐剖面资料和海表面信息构建了日平均三维温度分析场。张春玲等[11]提出了一个温度参数模型，并利用高分辨率SST 反演出太平洋上层海域气候态月平均三维温度场。利用目前大量的Argo 剖面数据已经开发出许多实时的月平均全球网格三维温盐产 品，例 如JAMESTEC 数 据 集[12]、Roemmich 数 据集[13]、EN4 数据集[14]和全球海洋Argo 网格数据集（Barnes Objective Analysis_Array for Real-time Geostrophic Oceanography，BOA_Argo）[15]。由于这些网格温盐产品的水平分辨率是1°×1°，原始观测数据的小尺度信号已经被平滑和隐藏，因此对于中尺度信号的研究是不够的。本文结合Zhou 等[16]提出的客观分析方法和Fox 等[17]提出的回归分析方法，针对Argo剖面混合层和下层分别利用分段线性拟合和多阶高斯拟合获得温度梯度剖面，再利用反向距离加权插值获得表层到下层网格梯度场，将海表温度作为初值代入梯度场在深度上的积分得到三维网格温度初始场；再基于历史观测的剖面资料，统计SSH 与温度剖面之间的相关关系，然后利用SST 和SSH 信息重构分辨率为0.5°×0.5°的三维温度分析场。

2 数据来源及处理

2.1 Argo剖面资料

Argo 剖面数据来源于Argo 数据管理中心（Argo Data Management），这些数据是由国际Argo计划免费收集和提供的（网址：http://www.argo.ucsd.edu,http://argo.jcommops.org），时间范围选取2004年1 月—2017 年4 月。 通过质量控制后共获得41 111个剖面数据。本研究选取的区域范围（140°～168°E、12°～36°N）内的剖面数量分布见图1，对剖面数据进行最优拟合得到每个剖面的梯度，利用反向距离加权插值（Inverse Distance Weighted，IDW）得到网格化的梯度场。

2.2 卫星遥感海表观测资料

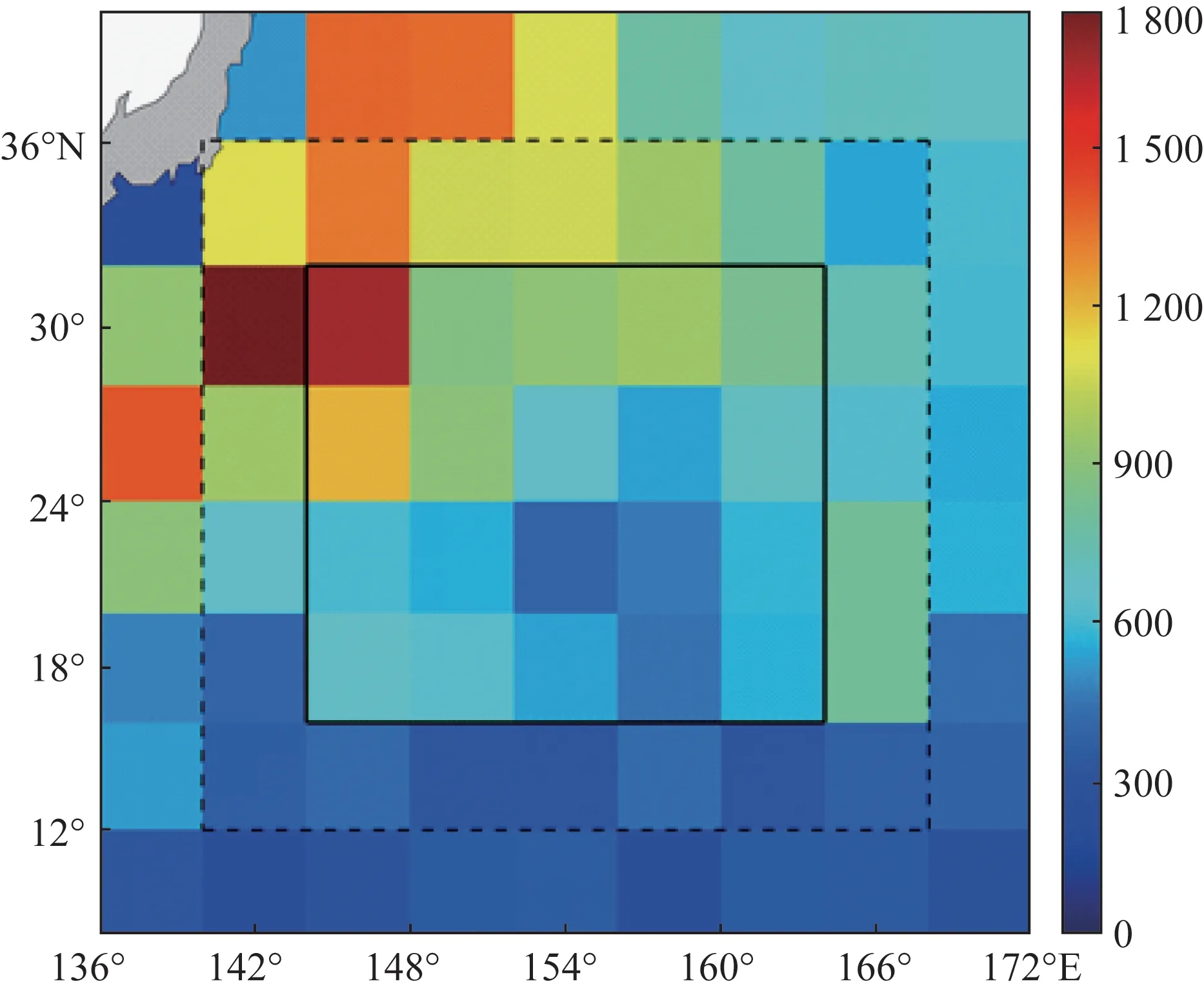
图1 研究区域与Argo剖面数量分布（黑色实线表示重构温度场范围，黑色虚线表示重构温度场所使用的Argo剖面的分布范围，颜色表示剖面数量，单位：个）

SST 数据来源于美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration，NOAA）甚高分辨率辐射计（Advanced Very High Resolution Radiometer，AVHRR）的每日最优插值SST（网址：ftp://eclipse.ncdc.noaa.gov/pub/OI-dailyv2/）。该数据结合了不同平台（卫星、船舶和浮标）的观测结果，网格分辨率0.25°×0.25°[18]。SST 数据用于初始化表面的重建算法，结合拟合的Argo温度曲线获得温度的垂直梯度，可以将SST 信息向下传递到中下层海洋。本文使用的海面高度异常（Sea Level Anomaly，SLA）数据来自于卫星海洋数据存储、验证、插值处理中心（Archivings Validation and Interpretation of Satellite Oceanographic，AVISO）提供的0.25°×0.25°的月平均网格化SLA 数据（网址：https://www. aviso. altimetry. fr/），该 数 据 融 合 了TOPEX/POSEIDON、JASON1/2和ERS1/2等卫星资料[19]，SLA 数据用来约束通过客观算法得到的三维网格温度初始场。

3 Argo三维网格温盐资料

本文选择两个现有的Argo 衍生网格产品（EN4.2.1 数据集和BOA_Argo 数据集）以验证重构温度场的精度。EN4.2.1 数据集（以下简称EN4）是英国气象局哈德利中心（Met Office Hadley Center）以《世界海洋图集1998》（World Ocean Atlas 98，WOA98）为背景场并通过最优插值方法生成，合并了所有类型的海洋剖面仪器的温度和盐度信息得到最新版本的数据集[14]。BOA_Argo 数据集（以下简称“BOA”）是基于Barnes客观分析由Cressman逐步订正法结合原始Argo观测资料生成的数据集，该数据保留了Argo 原始数据的信号[15]。这两个数据集的质量相对较好，两者都用于结果的对比分析。

4 研究方法

本研究中数据的处理分析分为3 个步骤（见图2）：第一步对数据进行质量控制，第二步利用SST和Argo数据客观分析得到三维网格温度初始场，第三步利用SLA 信息通过回归分析得到约束后的三维温度分析场。

第一步：Argo 剖面数据经过原始的质量控制，仍有一些有质量问题的数据包含在剖面中，为了确保数据集的可靠性，本研究对Argo剖面数据进行温盐范围检验、尖峰检验、温盐梯度检验及水深递增检验等质量再控制。研究用到的SST 数据是日平均转化为月平均的SST数据。

第二步：利用Argo 剖面求出Argo 浮标所在位置的混合层深度hm，对于每一个单独的剖面，把数据分成两部分：混合层与下层。对于混合层的温度剖面，温度随深度变化较小，通过分段线性拟合得出混合层各层的温度梯度。

式中：T0为剖面第一层海水温度；Ti表示剖面第i层海水温度；Ti所在的深度表示为hi，即混合层深度hm。

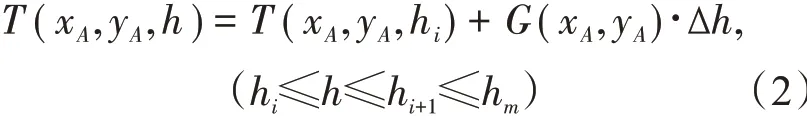
式中：Gi(xA,yA)表示第i层与第i+1 层的温度梯度，即混合层拟合函数的导数，计算公式如下：

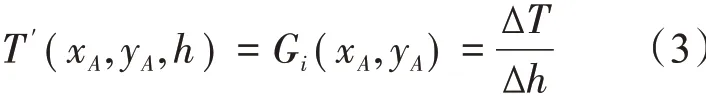
通过对下层温度剖面的统计分析，发现下层温度剖面符合高斯函数的特征，所以在下层温度剖面采用多阶高斯拟合，拟合函数如下：

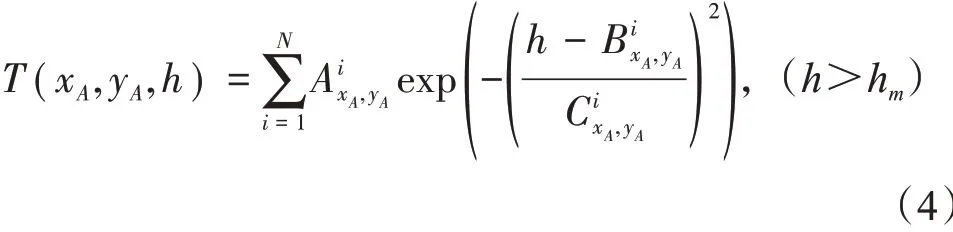
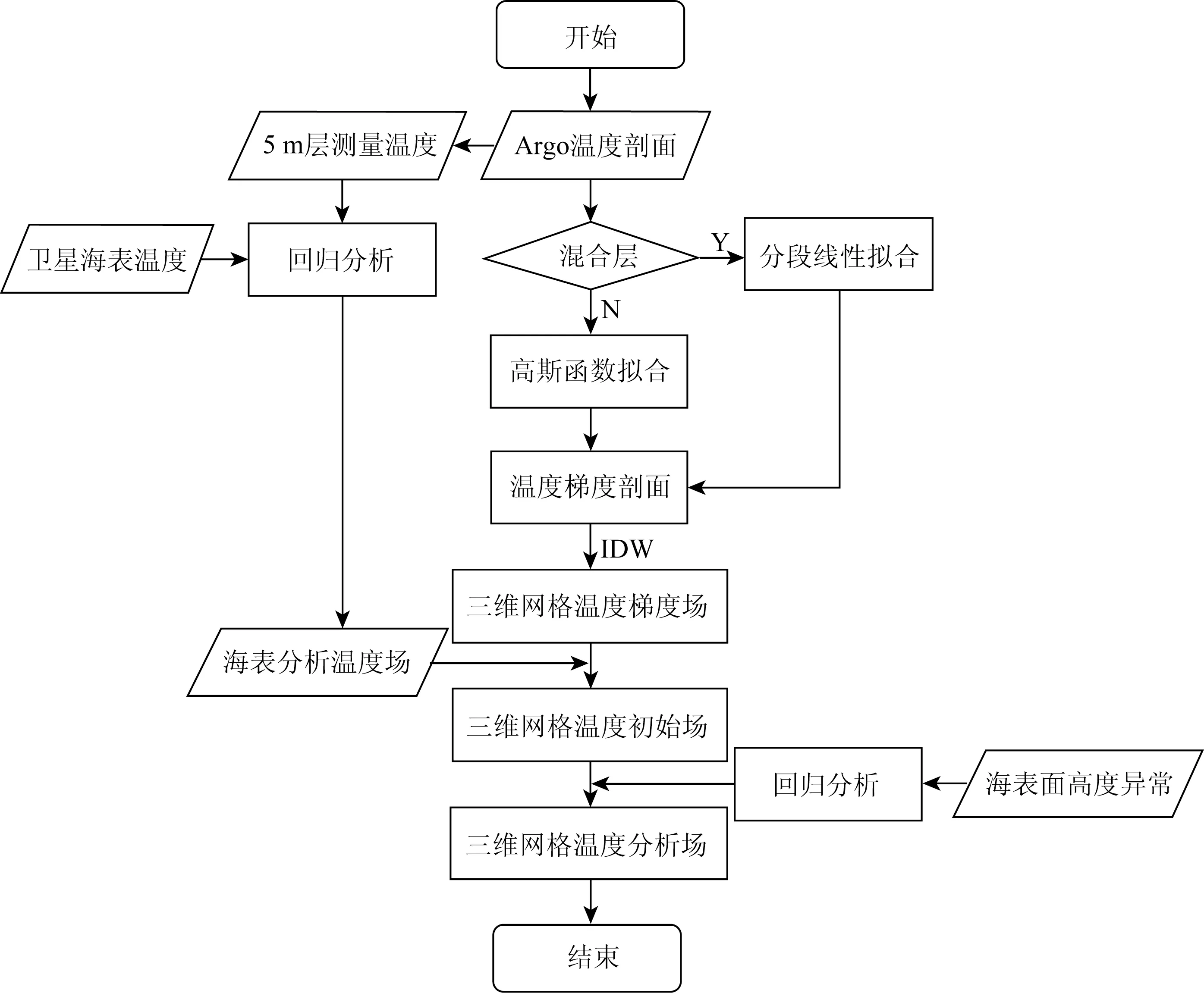
图2 数据处理分析流程图

系数Ai、Bi和Ci通过最小二乘法确定，N表示高斯函数的阶数。选择不同的N对拟合结果会有较大的影响，在本研究中选择N=4 时，拟合温度与观测温度的均方根误差（Root Mean Squared Error，RMSE）较小（见图3），当N=5 时，会产生过拟合，虽然误差变小，但拟合结果在上层较差。对拟合函数进行求导得到下层的温度梯度，公式如下：

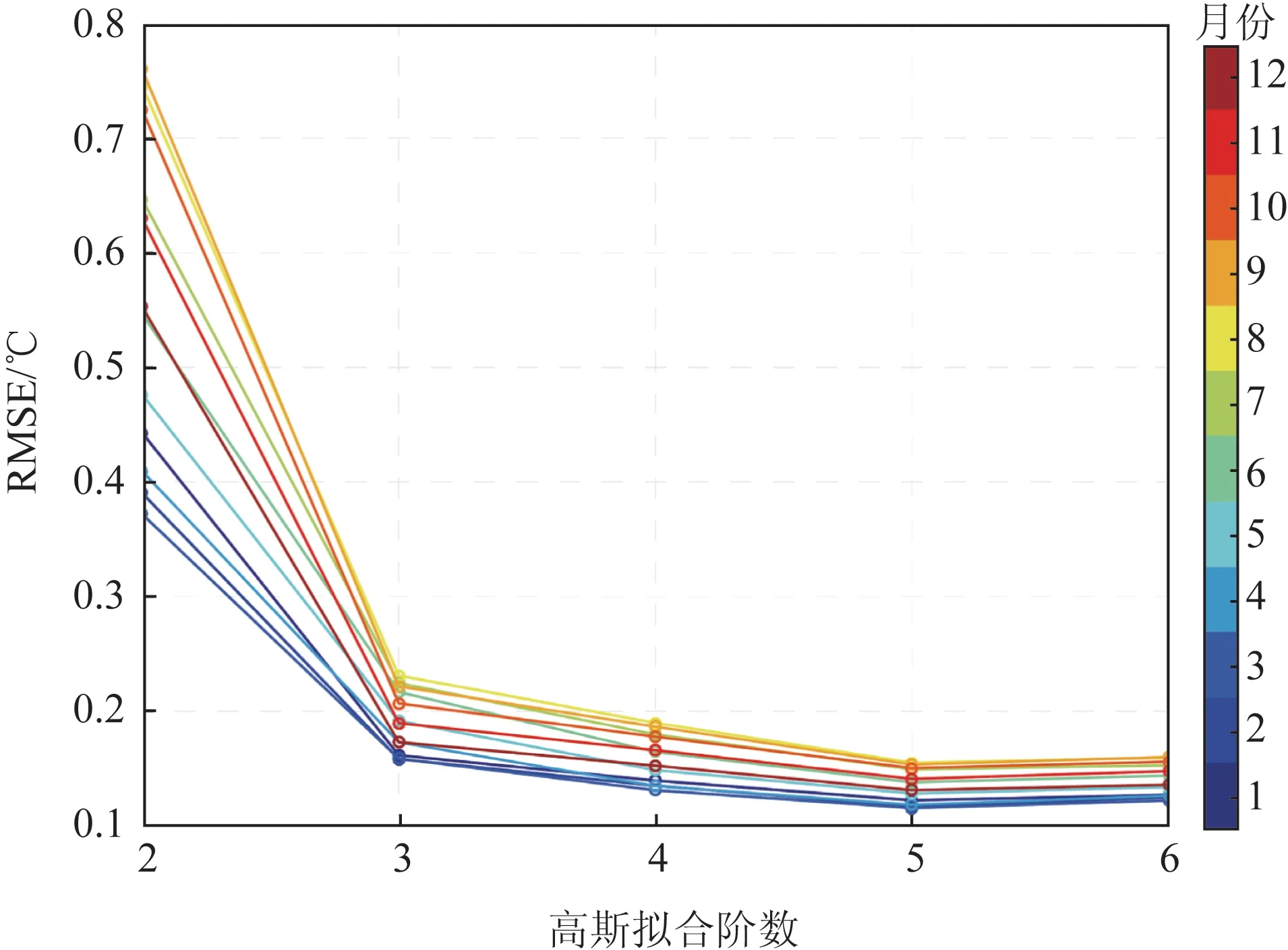
图3 不同阶数下拟合曲线与观测数据的RMSE

通过式（3）和式（4），得到整个剖面所有深度层上的温度梯度T'(xA,yA,h)，利用反向距离加权插值对所有梯度剖面进行网格化，得到网格化的梯度场T'(xg,yg,h)。对网格温度梯度场在深度上进行积分，将5 m 层的温度T0(xg,yg,h0)作为初值代入，得到三维网格温度初始场Ti(xg,yg,hi)，公式如下：

由于Argo浮标第一层的深度不完全相同，本研究将4～6 m 之间的温度当作Argo 浮标5m 层的温度场T(xA,yA,5 )，利用卫星观测的SST 数据与Argo浮标5 m 层的温度进行线性回归分析，发现表层SST 与5 m 层的温度存在较强的相关性（见图4a），a和b分别为线性回归所得出的系数，5 m层的网格温度场T0表示为：

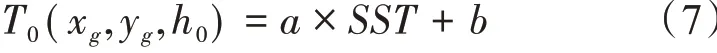
第三步：利用第二步得出的三维网格温度初始场和由温盐剖面资料计算的动力高度，采用回归分析方法，建立海面动力高度与次表层温度之间的映射关系。首先计算两个位置点的相关尺度系数CSFi,j，计算公式如下：

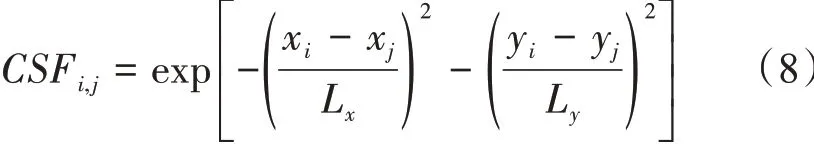
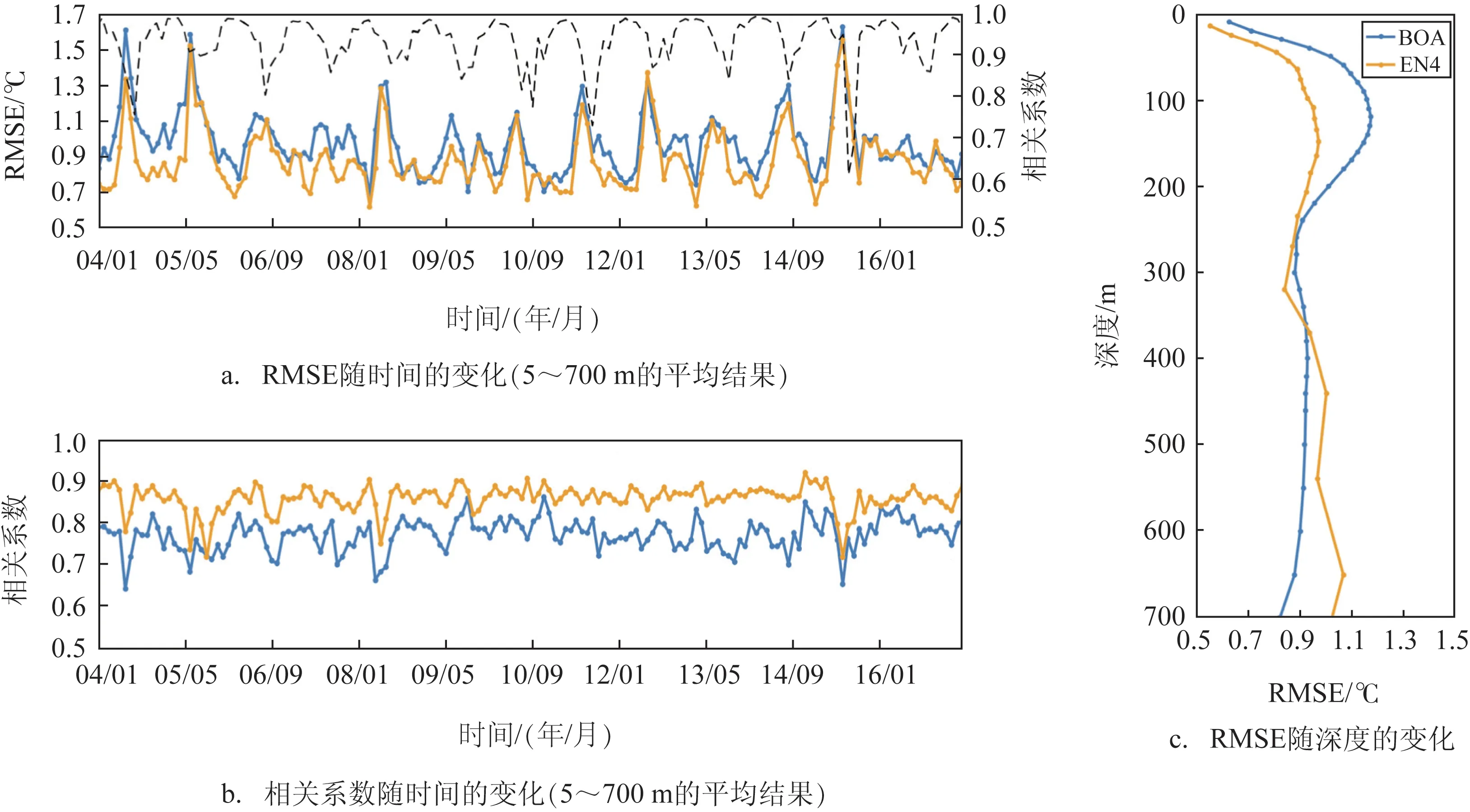
图4 三维网格温度初始场与验证数据RMSE和相关系数的对比图（蓝线：BOA数据集；黄线：EN4数据集；黑色虚线：SST与Argo浮标5 m层的温度相关系数）

式中：Lx和Ly分别表示经度和纬度相关尺度，利用得到的相关尺度系数计算分析温度场的加权平均-T xg,yg,k，再利用温盐剖面资料计算动力高度h，本文由Olber等[20]的定义来计算动力高度：

式中：ν 是海水比容，ν( 0,35,p) 为海水温度为0 ℃、盐度为35 时的海水比容，称为标准比容，h表示参考层深度，本文选取参考深度为700 m。回归系数计算如下：

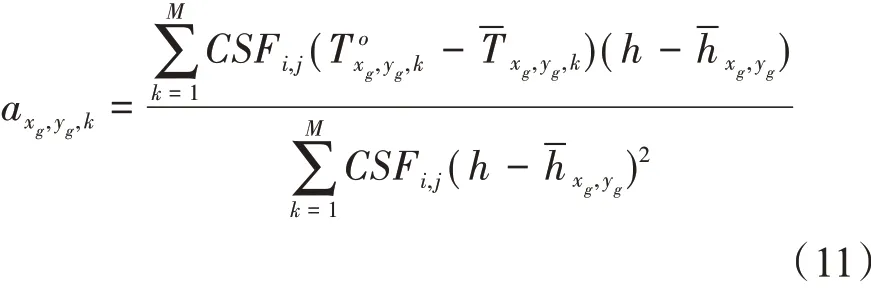
温度剖面与SLA之间的函数关系为：

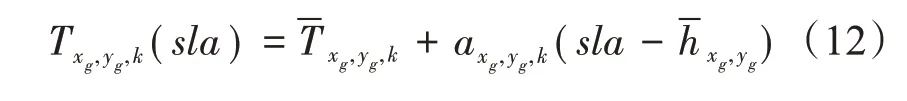
式中：hxg,yg为（xg,yg）比容高度异常的加权平均，类似于式（9）求得，sla为卫星观测SLA 值，最后将AVISO 提供的SLA 数据代入式（12），得到经过SSH信息约束的三维温度分析场，在本文中简称为基于客观分析的温度重建法（Reconstructed Temperature based on Objective Analysis Method，ORT)。

5 结果与分析

通过ORT 法得到三维网格温度初始场，再通过SLA数据对得到的三维温度初始场进行约束，得到更加优化的三维温度分析场。为了证明此方法的可行性，在本研究中使用BOA和EN4数据集进行验证，验证分为两个部分：第一部分对三维网格温度初始场进行验证，第二部分验证最终的三维温度分析场。

5.1 三维网格温度初始场的验证

将三维网格温度初始场与EN4 和BOA 数据分别进行比较分析。分别计算了该三维温度场与EN4 和BOA 的均方根误差，结果表明：前者比后者小，即得到三维网格温度初始场和EN4 数据集更接近（见图4a）。与两种验证数据相比，RMSE 大小存在周期性变化，原因是海表SST 与Argo 浮标5 m 层的温度相关系数出现了周期性变化（见图4a）。从图4b中可以看出，三维网格温度初始场与EN4的结果相关性优于BOA，并且相关系数表现出与RMSE相类似的特征。不同深度的验证结果表明，RMSE随深度逐渐增加，到100 m 达到最大，然后又逐渐减小，然后基本保持稳定（见图4c）。由于0～200 m层一般处于混合层，温度变化不规律，在进行数据分析时采用的是分段线性拟合，导致上层的温度误差较大。200 m 以下一般处于温跃层，温度变化规律，随深度增加而下降，在进行三维温度场的构建时采用多阶高斯拟合，所有剖面拟合得到的结果与观测数据的RMSE 均小于0.20 ℃（见图3），可以很好地反映观测数据的结果，所以200 m 层以下的温度误差要小于上层。总体而言，通过ORT 得出的温度初始场能基本反映各层的温度特征，温度的空间分布与验证数据存在一定的相关性。

5.2 三维温度分析场的验证

为验证ORT 的精度，首先对温度的空间分布进行验证。选取2016 年1 月、4 月、7 月和10 月代表4个不同季节的100 m 层与500 m 层温度场（见图5和图6），分别与BOA 数据集和EN4 数据集进行对比。4 个季节100 m 层温度的空间分布特征与验证数据基本吻合，温度梯度都是从低纬指向高纬，而且ORT 与BOA 数据集都表现出更多小尺度的温度变化信号，这一点在EN4 数据中没有体现。500 m 层的温度分布特征同样基本相同，但是ORT与EN4的结果相关性要高于BOA。由于黑潮的影响，500 m层温度梯度从高纬指向低纬，暖水逐渐向东延伸，这一特征在ORT 中也有明确的体现。通过对ORT数据空间分布的验证，表明客观分析方法重构三维温度场具有可行性。

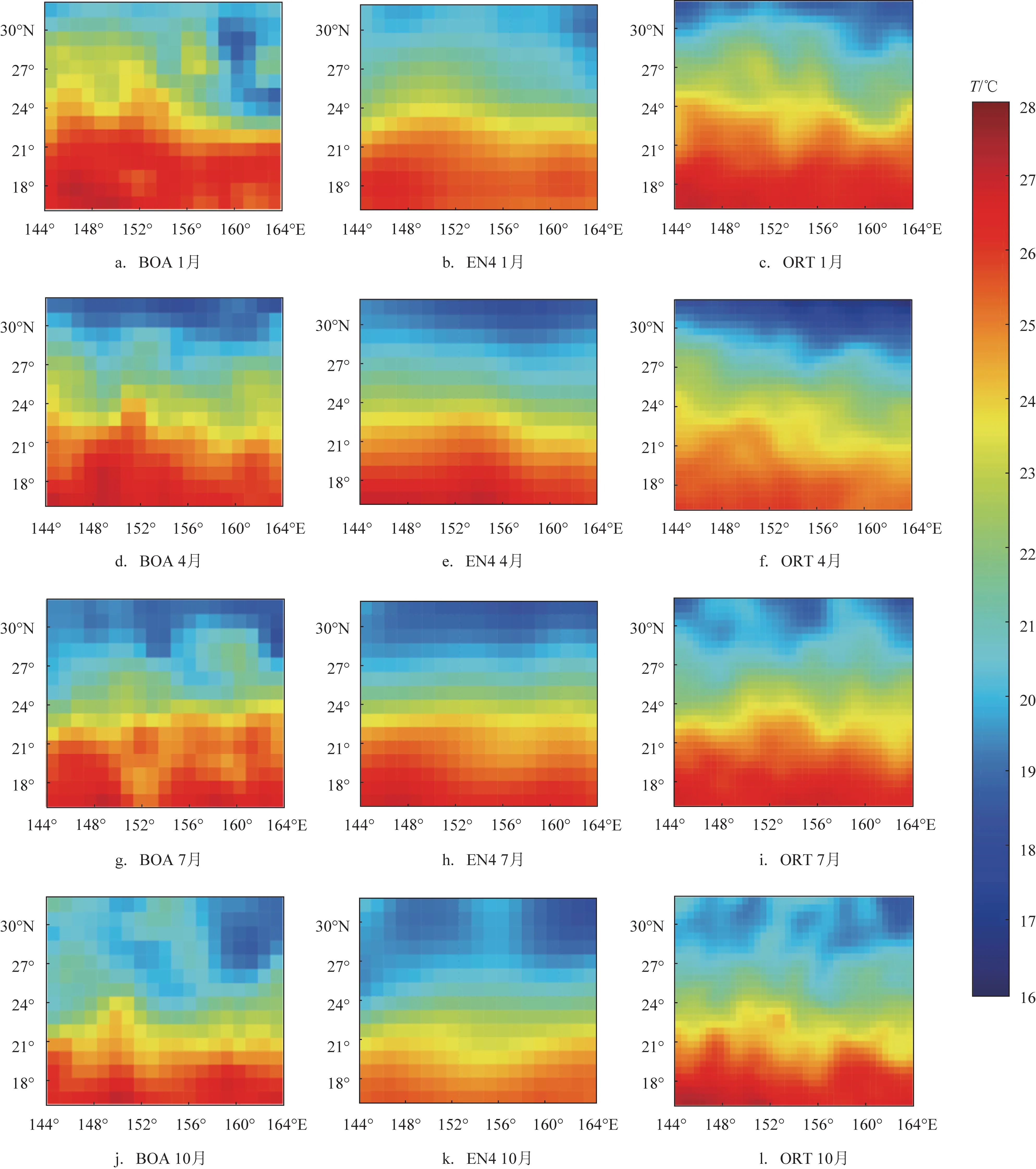
图5 2016年1月、4月、7月和10月100 m层温度空间分布对比图

选取2004 年1 月—2017 年4 月共160 个月份的数据对ORT 进行时间序列的对比分析。如图7 所示，ORT 相对于BOA 数据集RMSE 为0.92 ℃，相关系数为0.99，偏差为-0.30 ℃；ORT 相对于EN4 数据集RMSE 为0.80 ℃，相关系数为0.99，偏差为0.27 ℃。ORT 与验证数据的对比结果证明重构的三维温度分析场与BOA 和EN4 的相关性系数均为0.99，在不同的深度上温度偏差≤0.30 ℃。针对每个月份的结果进行对比分析，结果如图8 所示，在SST与Argo 浮标5m 层的温度相关性系数较低时，RMSE 与初始场误差结果无明显降低，最大误差达到1.6 ℃；逐月结果与两个不同的验证数据的相关性系数相对于三维网格温度初始场结果明显增大。同样在SST 与Argo 浮标5 m 层的温度相关性系数较低时，ORT 与验证数据集的相关系数与初始场相关性结果相同（见图8b）。我们选取ORT 5～700 m层的逐层求RMSE，并与初始场的RMSE对比，两种验证数据的结果都有明显提升，相对于BOA 的RMSE 降 低0.10 ℃，相 对 于EN4 的RMSE 降 低0.12 ℃，随深度变化趋势与初始场结果一致（见图8c）。通过对ORT 结果的时间序列变化以及垂向结构验证，表明ORT 数据和验证数据具有很好的相关性，能较好的反映下层温度的垂向结构变化特征。

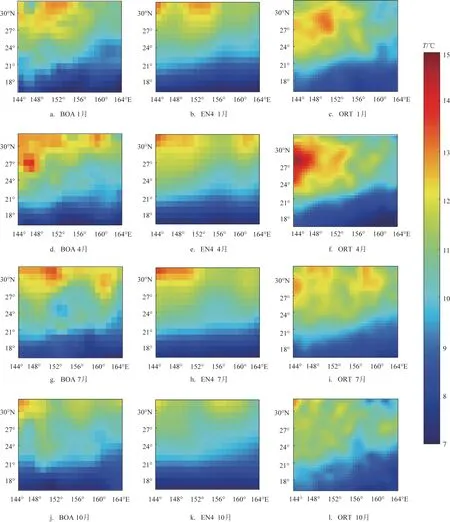
图6 2016年1月、4月、7月和10月500 m层温度空间分布对比图

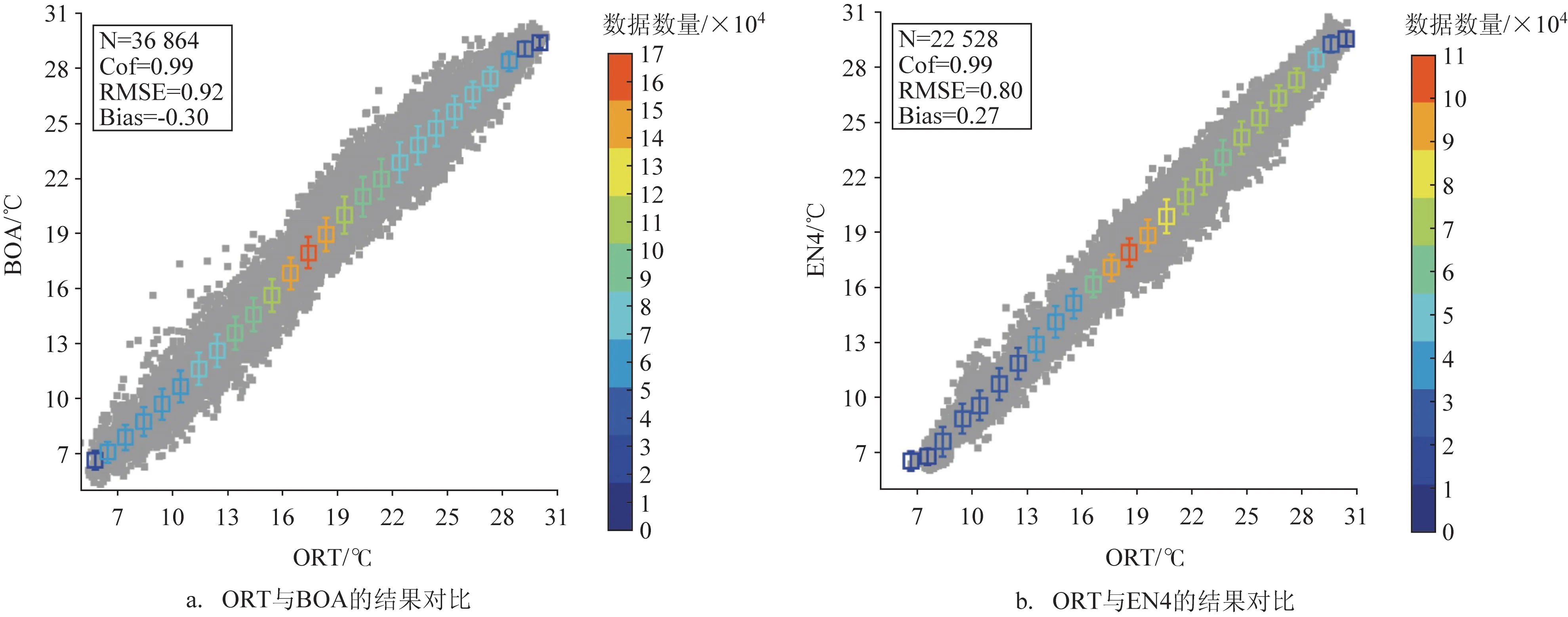
图7 ORT与BOA和EN4验证数据的误差对比（数据来自5～700 m，灰色表示ORT和验证数据的散点，间隔50 m取一个点，误差棒表示1 ℃范围内的平均值和偏差，颜色表示范围内数据的数量）

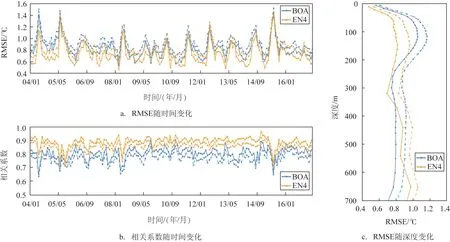
图8 ORT与验证数据的均方根误差对比以及相关性对比（数据为5～700 m平均结果，蓝线表示BOA数据集，黄线表示EN4数据集，实线表示经过SLA数据约束的结果，虚线表示没有经过SLA数据约束的结果）

6 结论

本文利用客观分析方法并加入海表面温度信息和海表面高度信息重构得到的分辨率为0.5°×0.5°的月平均三维温度分析场，垂向深度5～700 m，垂向分辨率1 m（5～300 m）和10 m（300～700 m）。经过空间分布对比验证以及时间序列的对比验证，ORT 在这两个方面相对于温度初始场都出现明显的改进，并且相对于验证数据都存在较高的相关性和较小的误差。由于加入了海表温度和海面高度信息，ORT 能够较为真实地反映海洋温度场的垂向结构变化特征，能将SST 信号的特征反映到混合层，并且能反映下层水团的变化过程和特征。本研究所得出的三维温度分析场可以用于研究下层小尺度温度变化特征，也可以作为模式初始场改进模式对海洋下层温度的模拟结果。