JB 4732—1995中锥壳与圆筒连接加强段设计方法的改进
2020-11-09薛明德吴坚李世玉
薛明德,吴坚,李世玉
(1. 清华大学,北京 100084;2. 中国石化工程建设公司,北京 100101)
1 研究背景
原行业标准JB 4732—1995《钢制压力容器——分析设计标准》(2005 年确认)[1]中无折边锥壳与圆筒连接加强段的设计方法形成于20 世纪八十年代末、九十年代初[2],其中对于锥壳大端的适用范围仅限于α≤30°,对于锥壳小端仅限于α≤45°,超过此范围必须设置圆环壳折边过渡。当大、小端圆筒直径差别较小、连接二者之锥壳变径段较短的结构,没有给出设计方法。设计方法多数情况下仅限于0.002 ≤pc/KSm≤0.1。此外,当锥壳小端与圆柱壳连接时,连接处有较高而分布范围超出“局部”薄膜应力定义的局部薄膜应力,控制加强段设计厚度的是局部薄膜应力PL;原JB 4732—1995 采用设计准则为应力强度SII≤1.1Sm,但在最近的美国ASME 规范[3]中,却将准则SII的许用值修改为1.5Sm。究竟应当采取何种设计准则也必须加以研究。为将锥壳大端和小端与圆筒连接加强段的适用范围统一扩大至α≤60°,0.001 ≤pc/KSm≤0.1 ,对此进行了二十多年的研究工作,发现必须对该方法的力学理论基础进行深入分析。问题主要包括以下两个方面。
1.1 薄壳理论简单边界效应解的局限性
在JB 4732—1995 中,锥壳的应力分析方法是基于薄壳理论的简单边界效应解。轴对称锥壳边缘效应的薄壳理论方程本来是一个复杂的四阶变系数常微分方程[4]:
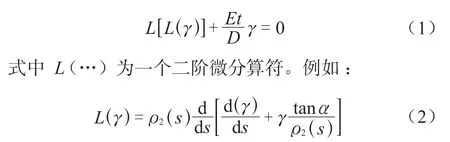
式中s为锥壳的经向坐标,锥壳经线转角γ= dw/ds,锥壳各点不同的第二曲率半径ρ2=r/cosα,r为所分析点处锥壳的平行圆半径。
由于薄壳中边缘效应具有沿经向从边界向壳体内部迅速衰减的特点,在一定条件下可将上述方程简化为一个当量圆柱壳方程,所求得的解称为简单边界效应解。简化的假定是:
(1)只研究锥壳一个边界附近小范围(2ρ δ量级)内的应力状态,假设此时锥壳第二曲率半径的变化可以略去,取该边界处的第二曲率半径ρ2b(常数)为微分算子中的变量ρ2(s)。此基本假定决定了不能考虑锥壳两端边缘效应耦合的情况,加强段中的锥壳必须取得足够长。
(2)微分算子的第2 项与第1 项相比是一个小量,可以略去。由于边缘效应自边界向内迅速衰减的性质,对经向坐标每求一次导数就乘一次壳体常数ks,所以:
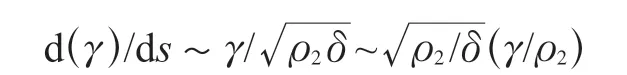

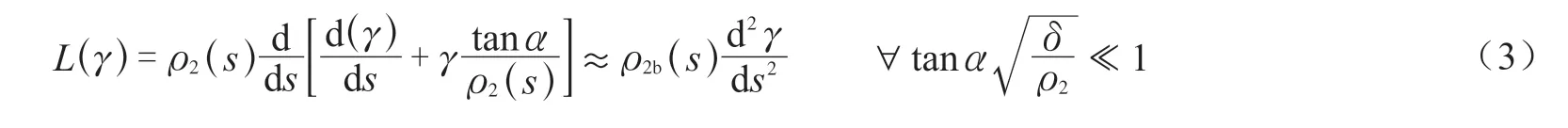
将近似式(3)代入式(1),锥壳方程近似地化为与圆柱壳方程类似的4 阶常系数常微分方程,即所谓当量圆柱壳方程。当量圆柱壳的半径为锥壳边界处的第二曲率半径ρ2b=rb/cosα,在锥壳大端和小端附近,rb分别取R2或R1。其解称为简单边界效应解。

1.2 按照弹性名义应力的应力分类法确定设计准则的局限性
JB 4732—1995 中与圆柱壳连接的锥壳大端处,采用一般的应力分类法设计准则;而在锥壳小端处,由于局部薄膜应力的分布范围通常都超出“局部”的定义范围,故采用设计准则为SII≤1.1Sm。所以,JB 4732 中锥壳与圆柱壳相连接处加强段的补强设计准则为:

其中,关于局部薄膜应力强度的准则(5)源自一维梁-杆模型的塑性分析,作为板壳这种二维承力结构的设计准则往往出现问题,有时安全裕度不够,有时又过于保守。特别是如果锥壳很薄,如pc/KSm在0.001 附近,式(5)的设计准则是否安全是需要研究的;又当锥壳变径段很短时,此准则该如何取?按照清华大学课题组早期关于塑性极限分析理论解的研究结果[5],若取SII≤1.5Sm,则结构的安全裕度不够。要解决此问题,必须在设计准则方面按防止整个结构(包括大、小端的两个圆柱壳和连接它们的锥壳)的塑性垮塌失效来分析,即对整个结构进行塑性极限分析。
2 无折边锥壳变径段设计方法之理论基础
本文所提出的无折边锥壳设计方法的制定依据是清华大学课题组20 多年的研究成果。
2.1 采用薄壳理论中锥壳的精确解,提高了解的精度,扩大了解的适用范围
薄壳理论关于锥壳的精确解[6]从锥壳的薄壳基本方程(1)出发求解,其通解的形式是汤姆逊函数与开尔文函数的组合,我们将表达为矩阵形式的结果给出在JB 4732—1995 的附录A 中,并且同时给出了锥壳两端与圆柱壳相连接的协调方程的表达式;但JB 4732—1995 并未给出便于工程设计的具体方法。在文献[7]中,进一步给出了变径段的应力分析方法。分析的力学模型见图1。图1 显示锥壳变径段的加强部分之基本几何参数为R1、R2、α和δ。采用此力学模型,既可给出短锥壳加强段的设计方法,当R2/R1足够大时,也可分别给出锥壳大端或小端与圆筒连接加强段的设计方法。

2.1.1 锥壳两端广义位移与内压和广义内力素的关系
设锥壳两端所受广义内力素矩阵为F,它由齐次解与压力p引起的薄膜解共同构成。锥壳的齐次通解中有四个待定常数,以矩阵c表示,它们由锥壳两端作用的广义内力素F唯一地确定,形成锥壳中的边缘效应。设锥壳两端边缘广义内力素矩阵F和锥壳边缘效应中的待定常数c矩阵,矩阵元素为 :
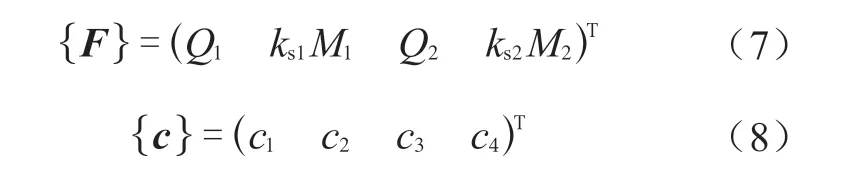
式(7)中ks1和ks2分别为小端和大端圆筒的壳体常数,由R1和R2分别代入文献[1]之A.2.1.1 节中ks的表达式得到。它们之间满足下列关系式:
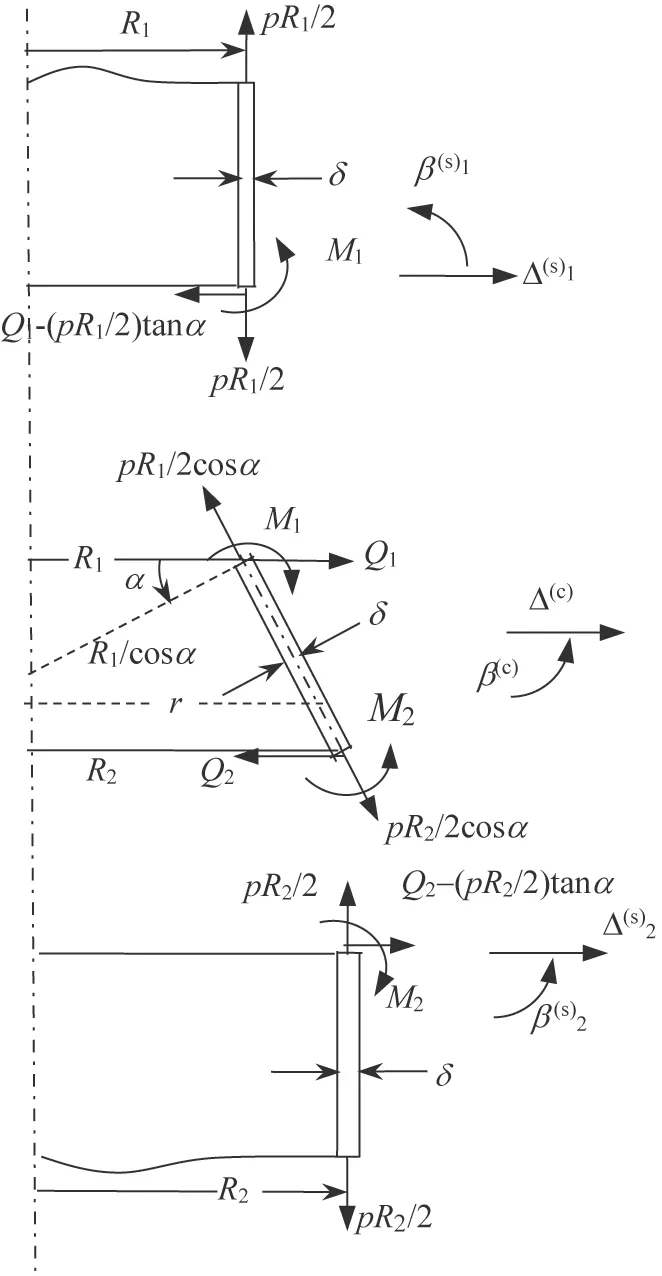
图1 弹性薄壳理论分析的力学模型Fig.1 The mechanical model based on elastic thin shell theory
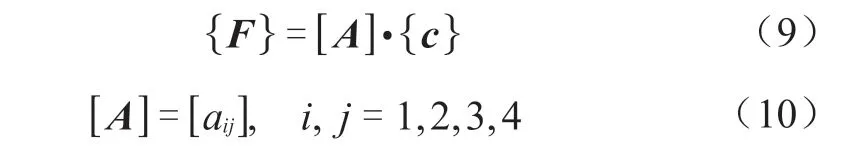
式中,A是4×4 的无量纲系数矩阵,系数aij之表达式见附录A 之式(A.2-20)。设锥壳两端广义位移列阵为u(c),由压力作用下薄膜位移uc*叠加锥壳边缘内力F引起的边缘效应位移(取决于常数c矩阵)构成。
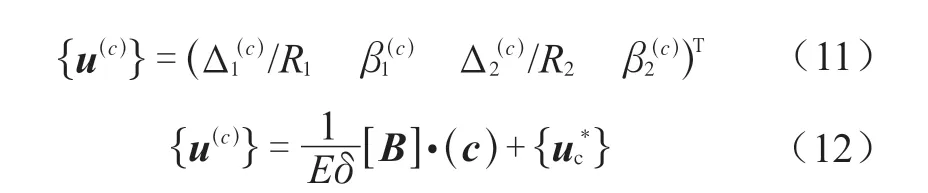

2.1.2 大小圆筒边缘广义位移与内压和广义内力素的关系
由圆柱壳的薄壳理论解,可以求得在内压p与边缘载荷作用下,大、小圆柱壳的广义位移。根据小圆柱壳与锥壳连接处内力素的连续条件(A.3-11)、大圆柱壳与锥壳连接处内力素的连续条件(A.3-14),得到:
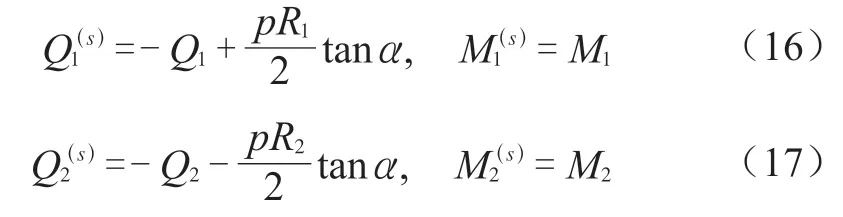
将上述二式分别代入式(A.2-1)、(A.2-4)、(A.2-5),可以分别得到小端、大端圆柱壳在与圆锥壳连接处的位移与转角,将其表示为矩阵形式:
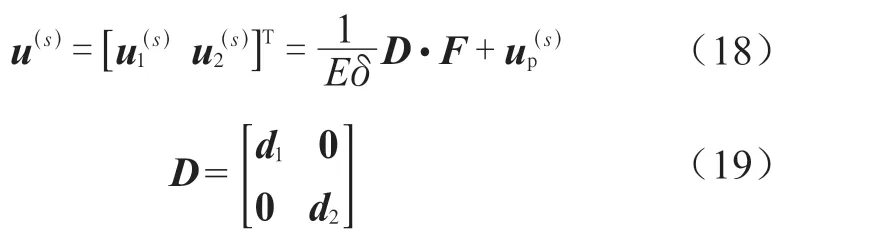
其中:
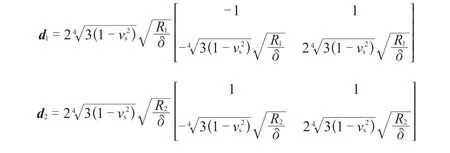
式(18)中第2 项up(s)是由内压p引起的圆柱壳广义位移,包含了(A.2-1)式的薄膜位移和 式(16)、(17)中由压力引起的部分齐次解。
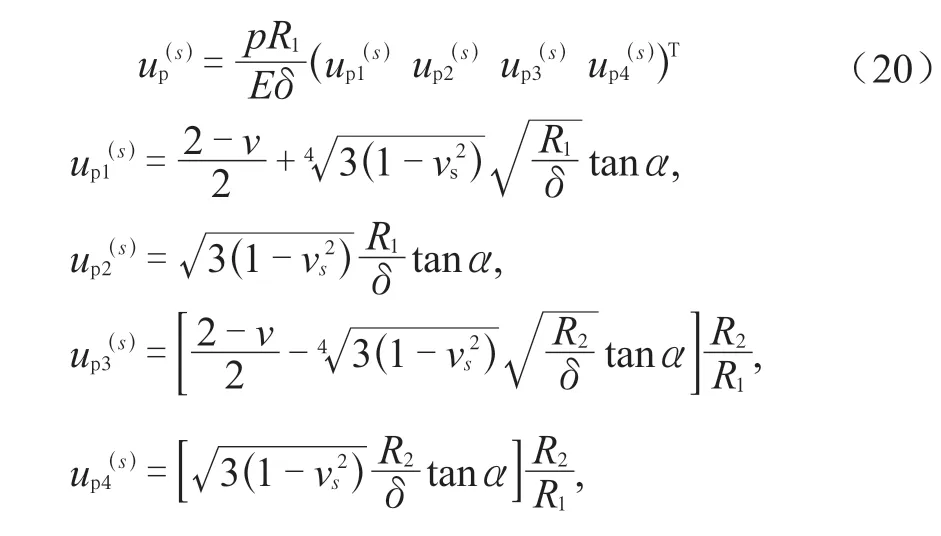
2.1.3 锥壳两端与大小圆筒边缘的变形协调方程
由锥壳两端r=R1,r=R2处分别与小端圆柱壳和大端圆柱壳的变形协调条件:

求解式(22),便可得到连接内力素F。
2.1.4 由连接内力素求壳中应力
由F可经式(9)求逆进一步求得锥壳中与边缘效应解相关的系数列阵c:

2.2 设计准则:基于塑性极限压力提出关于局部薄膜应力的设计准则
假设材料为理想塑性,清华大学课题组依据塑性极限分析的理论解[5]、理想塑性轴对称体的有限元分析[8]保证了结构塑性极限压力与设计压力之比有不小于1.5 倍的安全系数;通过弹塑性大变形非轴对称壳有限元分析保证当p/Sm最小在0.001 时结构不发生内压失稳[8]。即仍保留设计准则式(4)、(6),以下列基于塑性极限压力的准则式(25)取代准则式(5):

式中ps——结构的塑性极限压力;
p——设计压力。
上世纪后期,清华大学徐秉业、薛明德指导其博士生杨波对锥壳大、小端分别连接大、小圆柱壳的结构导出了塑性极限分析的理论解[5],其力学模型见图2。文献[5]对两个圆柱壳采用单矩弱作用的Tresca 屈服条件,对圆锥壳采用双矩弱作用的Tresca屈服条件,得到了极限分析的完全解。文献[5]给出不同几何参数(α、R2/R1、δe/R1)条件下结构可能发生的5 种不同的塑性流动模式(见图3)及其与这些参数的关系,图4 给出其中锥壳两端边缘效应不耦合的算例(R2/R1=1.5)。其中机构A 为锥壳大端与大圆柱壳先破坏,发生在α和R2/R1较大、δe/R1较小时;机构C、D 为锥壳小端与小圆柱壳先破坏,机构E 为小圆柱壳先破坏,这三种机构发生在α和R2/R1较小时;机构B 为锥壳大、小端和大、小圆柱壳同时破坏,发生在几何参数为中间状态时。文献[5]还给出了每组参数(α、R2/R1、δe/R1)对应的无量纲塑性极限压力psR1/ (ReLδe),见图5,其中ps为塑性极限内压,ReL为材料的屈服应力。受当时研究条件所限,该项工作在制定JB 4732—1995 时未能进一步验证和应用。2017 年起,我们通过理想弹塑性小变形有限单元法[8]对文献[5]进行了验证,证明了文献[5]根据塑性理论完全解所给出各种参数下的结构塑性破坏机构与极限压力的可靠性。详见文献[8]。
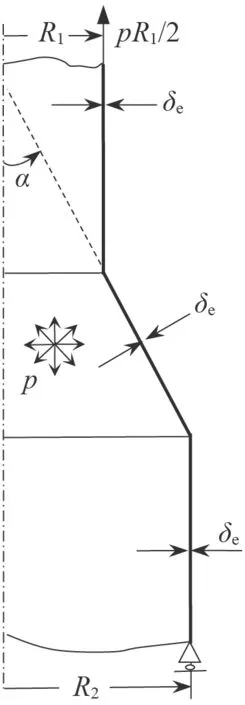
图2 塑性极限分析的力学模型Fig.2 The mechanical model of plastic limit analysis
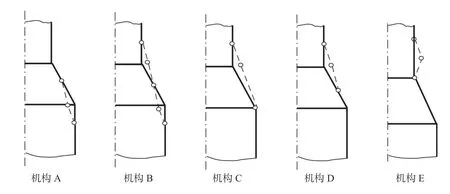
图3 5 种可能的塑性流动机构Fig.3 Five kinds of plastic flow mechanisms
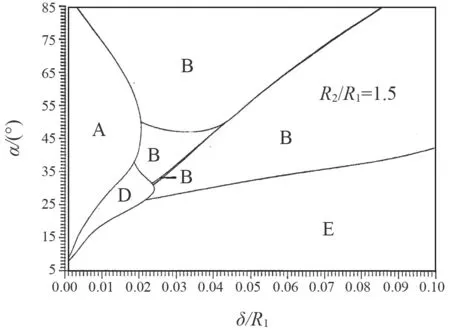
图4 锥壳变径段塑性流动机构与几何参数的关系 (R2/R1=1.5)Fig.4 The relations of plastic flow mechanisms to the geometrical parameters of conical reducers ( R2/R1=1.5)
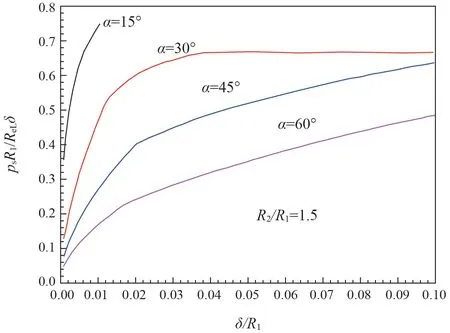
图5 极限压力与参数α, δ/R1 的关系Fig.5 The relations of plastic limit pressure to the geometrical parameters α, δ/R1
从图4 关于各种参数下的塑性流动机构可见,若结构参数α较小,在δe/R1较大的范围内,塑性极限分析理论解[5]指示总会发生图3 中D,E 两类塑性流动机构,即锥壳和小端圆柱壳先破坏,此时若计算弹性名义应力,则控制锥壳变径段设计厚度的准则必定为小端锥壳的SII。若α较大、δe/R1较小而R2/R1较大,塑性极限分析理论解[5]指示会发生图3 中A 类塑性流动机构,即锥壳和大端圆柱壳先破坏;此时若计算弹性名义应力,则控制锥壳变径段设计厚度的准则不仅可能为锥壳大端一次加二次应力强度SIV的准则式(6),也可能为该处的SII;这一点是在加强段大端设计中必须考虑的。
3 设计方法的制定原理
JB 4732—1995 中的设计方法已经为工程界所熟悉,新的应力分析篇仍旧保留该方法的形式,即对于锥壳与大端圆筒、小端圆筒分别连接时,给出加强段的设计厚度计算公式:

需按照本文的计算方法与设计准则给出加强系数Q的设计曲线。式(26)中Di为与锥壳连接的圆筒内直径,注意到若圆筒的计算厚度为δ、中面半径为R,δ/R=p/Sm,式(26)与式(27)完全等同:

由于应用弹性薄壳理论解便于进行大量的、连续参数的计算,容易为工程设计提供简明的公式与曲线图,所以在制定设计方法时应当综合两种计算方法的优点,互相补充。具体方法是:以弹性薄壳理论为基础,分别计算出各种参数下结构中的弹性名义应力强度SI、SII和SIV;应用设计准则式(4)、(6)以及(25)确定加强段设计所需的圆筒计算厚度之加强系数Q值;其中,对于要求满足准则(25)对应的结构厚度δe,计算对应的许多等距离离散点的塑性极限压力ps,通过试算使之符合式(25)要求,再计算该结构对应的弹性名义应力强度SII,根据这一系列对应不同结构参数下的SII值可拟合相应的满足准则(25)的SII许用值经验公式。然后,将式(5)中SII的许用值改为式(28):

弹性薄壳理论分析计算结果表明:当锥壳变径段较长时,锥壳两端的边缘效应将不会互相耦合。锥壳与圆柱壳连接时加强段的加强系数Q可分为三种结构给出:
(1)锥壳大端与圆筒连接;
(2)锥壳小端与圆筒连接;
(3)短锥壳两端分别与大端圆筒、小端圆筒连接。
此外,为扩大无折边锥壳与圆筒连接结构的适用范围,以降低制造成本,对无折边锥壳与圆筒连接接头,增加了关于对接焊缝(或角焊缝)的倒圆过渡的要求。通过基于轴对称实体单元的弹性有限元分析,确保结构的安定性。为使该设计方法扩大至适用于0.001 ≤p/Sm≤0.002 的范围,还对p/Sm= 0.001的结构进行了防止内压失稳的有限元分析。
4 锥壳大端与圆筒连接的加强段
4.1 连接结构几何形状与理论解的验证
为将无折边锥壳与圆筒连接方式的适用范围扩大至α≤60°,需要解决两个问题:一是降低连接处的应力集中,二是检查α= 60°时理论解是否仍旧能够适用。本文建议增加关于对接焊缝(或角焊缝)的倒圆过渡的要求,
图6 为一个典型算例的轴对称三维实体单元有限元计算网格图,在锥壳大端和小端与圆筒连接处,r0=δn(δn为加强段名义厚度)。将有限元计算结果与薄壳理论解进行对比,见图7 所示。若将实体单元计算结果沿截面进行线性化处理,可发现二者能够较好地吻合。经过对各种尺寸圆角的对比计算,确定当圆角尺寸r0不小于加强段名义厚度δn时,可以满足本小节所提的上述要求[7]。采用锥壳与圆筒连接处设置半径为r0=δn之过渡圆角的方法,直至锥壳半顶角α= 60°时都可以采用无折边加强段。
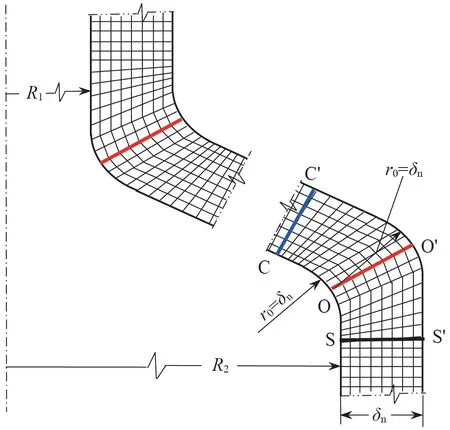
图6 锥壳与圆筒连接结构实例有限元计算网格图Fig.6 The FEM mesh of an example for the cone-to-cylinder junction
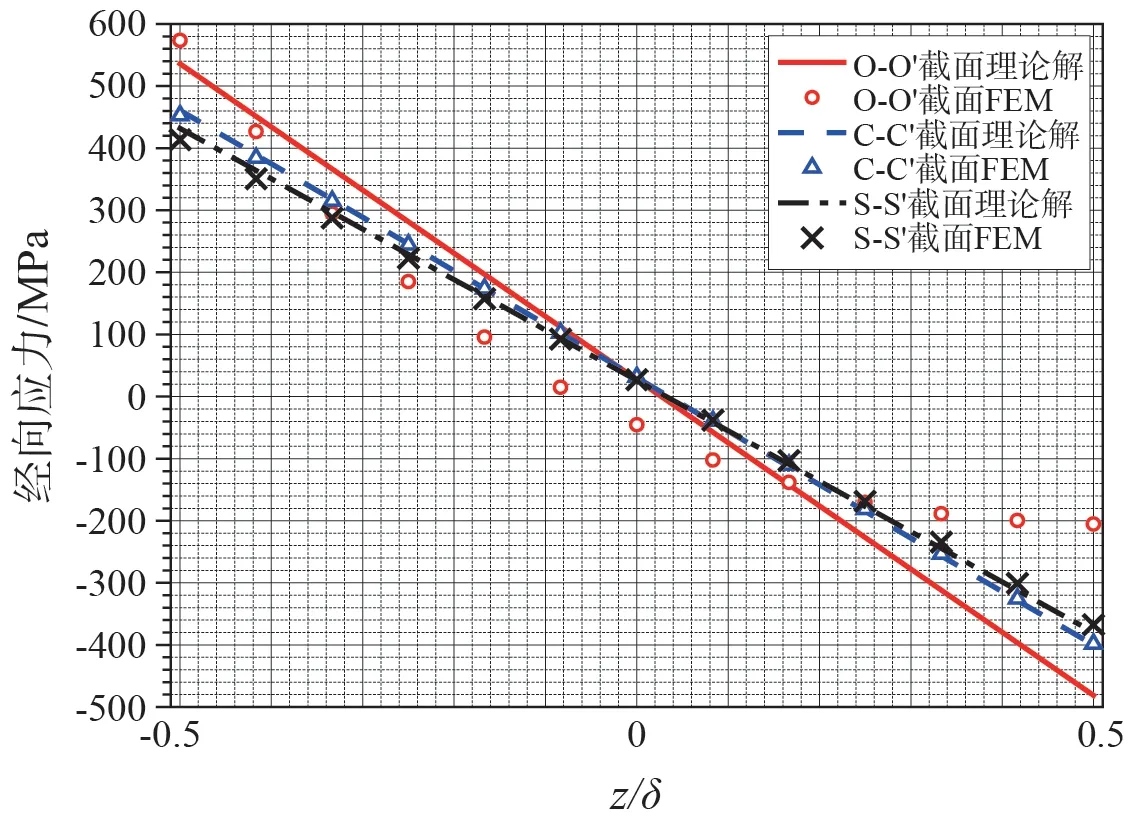
图7 锥壳与圆筒连接结构实例有限元计算结果与理论解比较Fig.7 The theoretical solutions of the example compared with the results calculated by FEM
4.2 当p/Sm= 0.001时结构塑性极限压力和稳定性的验证
薄壳理论分析发现,当锥壳大端与圆筒相连接时,在内压作用下连接处产生环向压缩薄膜应力与径向压缩位移,故当壳体极薄时,该处有发生内压失稳的危险[9-10]。文献[9]给出了三个锥壳大端与圆筒连接的内压失稳的模型实验,其中厚径比最小的一个为δ/R2= 0.001 9。为使所给加强段的补强设计方法扩展至0.001 ≤p/Sm=δ/R2≤0.002 的范围,需保证当p/Sm=δ/R2最小在0.001 时加强段不发生内压失稳。我们用轴对称实体单元,进行理想弹塑性小变形轴对称体有限元法分析结构的极限压力;又按照Schmidt、Krysik[11]提出的“等效几何缺陷建模法”,用非轴对称壳单元,进行理想弹塑性大变形有限元法分析该结构。图8 给出其中一个对于稳定性而言安全裕度最低的算例,其参数为:材料屈服极限ReL= 230 MPa,α= 60°,R2/R1= 1.8,R2= 1 800 mm,p/Sm= 0.001。算例厚度按本文建议方法计算,设计加强段厚度δn= 9.083 mm。由小变形有限元法所得压力-变形历史曲线给出塑性极限压力ps= 0.353 MPa;再由大变形有限元法所得压力-变形历史曲线给出结构产生1%塑性变形时压力为p1= 0.649 MPa,可见结构此时仍未发生失稳,仍有较大的承载能力。

图8 弹塑性有限元分析算例:内压—锥壳大端与圆柱壳连接点径向收缩变形历史曲线Fig.8 An example calculated by elastoplastic FEM: The elastoplastic radius displacements at large end intersection of the cone-to-cylingder versus the pressure
对具有其他锥壳半顶角的算例,按照与上述算例相同方法进行有限元分析,结果见表1。所有算例均保证其塑性极限压力有至少1.5 倍的安全裕量,满足设计准则式(30)。同时,理想塑性大变形分析得到的p1≫1.5p,说明按照该设计方法在所给适用范围内结构都不会发生内压失稳,控制加强段设计厚度的准则仍旧是防止塑性垮塌。
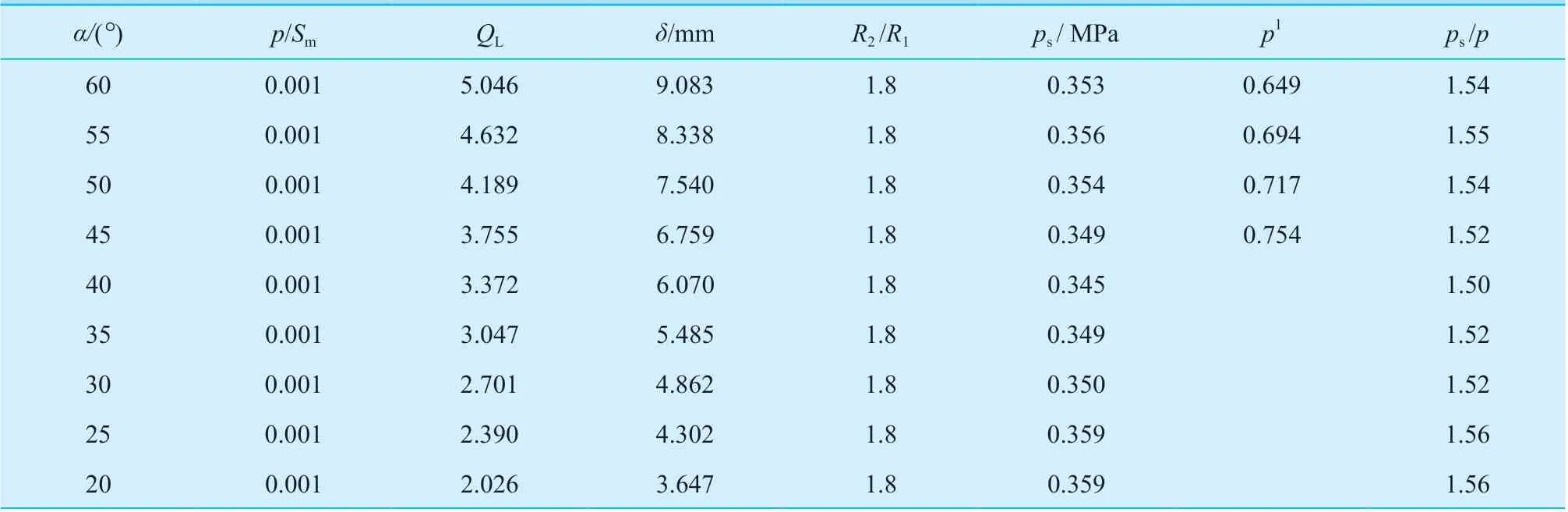
表1 与圆柱壳连接的锥壳大端结构理想塑性有限元分析的承载能力(p/Sm=0.001)Table 1 The limit loads of conical shell connected with cylinder at large end intersection computed by perfectly plastic FEM (p/Sm = 0.001)
按照弹性薄壳理论精确解和准则式(30),本文给出锥壳大端与圆筒连接时加强段的加强系数QL值,如图9 所示。图9 中离散的点为JB 4732—1995 所给的Q值,在p/Sm= 0.001 及其附近值处,JB 4732—1995 所给的Q值都略小于本文所给QL值,这是由于JB 4732—1995 没有考虑对于极薄的大端加强段也必须考虑防止塑性垮塌要求的缘故。
5 锥壳小端加强段
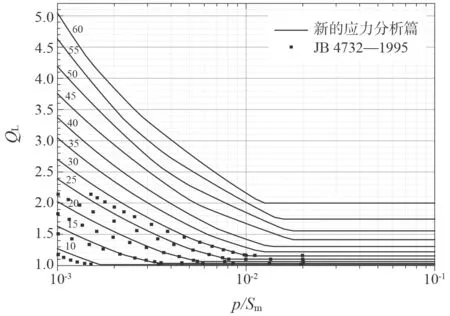
图9 本文锥壳大端加强系数QL 曲线与JB 4732—1995[1]对比Fig.9 The reinforcement coefficient QL for large end intersection of conical shells presented by this paper compared with JB 4732—1995[1]
按照弹性薄壳理论精确解和准则式(30),可得到锥壳小端与圆筒连接时加强段的加强系数Qs值,如图10 所示。塑性极限分析计算结果发现,按照我们所提出的设计准则式(25)和式(28)所确定的kII值,当锥壳变径段足够长,其大、小端边缘效应不互相耦合时,kII值比1.1 略大,但远小于1.5。说明ASME规范[3]所给设计准则安全裕度不够。图10 中离散的点为JB 4732—1995 所给的Q值,所有值都略大于本文所给Qs值。

图10 本文锥壳小端加强系数Qs 曲线 与JB 4732—1995 对比Fig.10 The reinforcement coefficient Qs for small end intersection of conical shells presented by this paper compared with JB 4732—1995[1]
为进一步说明本文所提出设计方法的可靠性,表2 给出了按照本文方法设计的一部分典型结构参数下加强段加强系数Qs值、kL值与ps/p值的比较,显示该标准设计方法有足够的安全裕度。
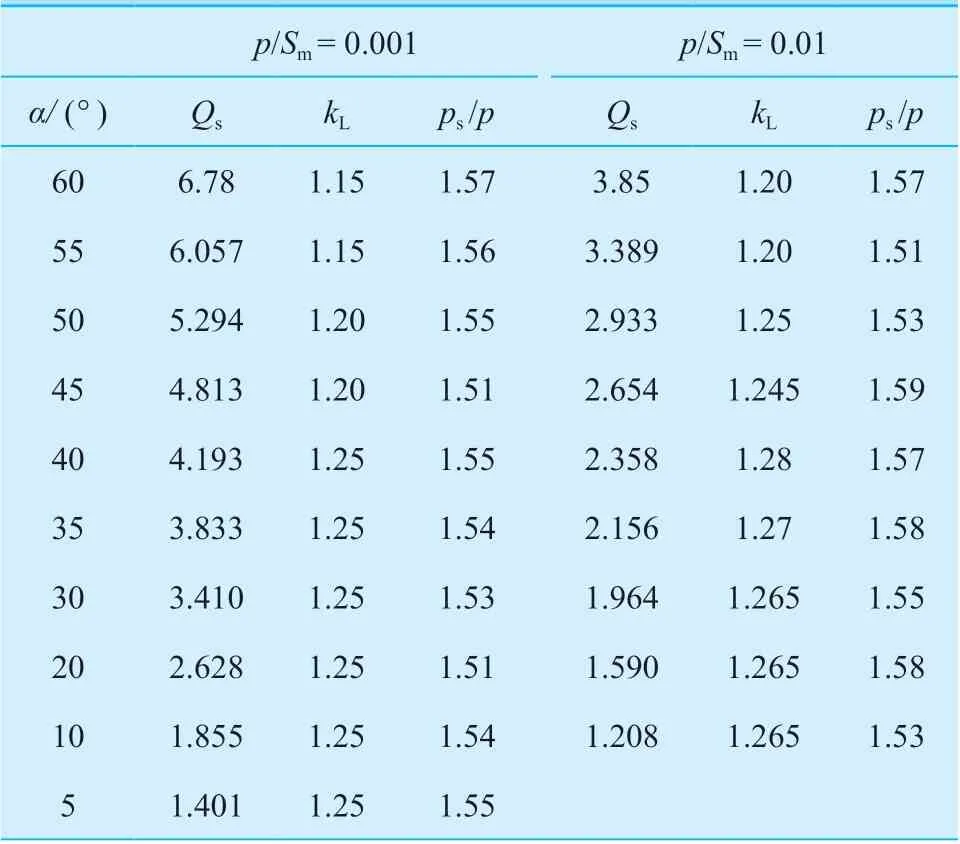
表2 按本规范设计锥壳小端与圆筒连接加强段的塑性极限压力Table 2 The plastic limit pressure of reinforcement for conical shell connected with cylinder at small end intersection presented by this paper
6 短锥壳两端分别与大、小圆筒连接的加强段
文献[8]给出一个短锥壳算例,计算结果验证了锥壳精确理论解的可靠性。分析发现对于短锥壳变径段,控制设计厚度的是小端处的薄膜应力强度式(28)、(29),其主要应力分量是环向薄膜应力。图11 给出该算例的环向薄膜应力薄壳理论精确解、简单边界效应解和有限元解的比较,显示薄壳理论精确解与有限元解可以很好地吻合,但简单边界效应解高估了连接处的环向薄膜应力。
按照弹性薄壳理论的精确解和准则式(25),可得到短锥壳变径段与大、小圆筒连接时加强段的小端加强系数Qs值,图12 给出其中α=60°时之一例,当R2/R1>1.35 时,就完全可以按长锥壳的图10 计算Qs。当锥壳过短、壳体达到一定厚度时属于结构不合理,故图中当p/Sm较大时曲线截止。当α<60°时,需要考虑耦合效应的最大R2/R1值随α值减小而减小。
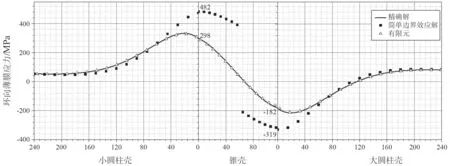
图11 短锥壳变径段环向薄膜弹性名义应力分量(α =60°, R1 =1 000 mm, R2/R1=1.1,δe/R1 = 0.006 25, p = 0.4 MPa)Fig.11 The nominal elastic circumferential membrane stress components in a short conical reducer (α=60°, R1 =1 000 mm, R2/R1 =1.1,δe /R1 =0.006 25, p=0.4 MPa)
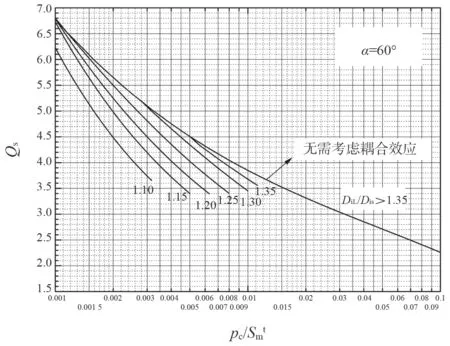
图12 α =60°短锥壳变径段大、小端边缘效应耦合时的Qs 值Fig.12 The reinforcement coefficient, Qs, for short conical reducer in boundary effect conjunction of two end intersections ( α=60°)
表3 给出本文所提出的考虑边缘效应耦合作用的短锥壳变径段设计方法所对应典型算例的极限压力,并同时给出这些算例对应的Qs值和kII=SII/Sm值。表3 还指出对于这些锥壳变径段非常短、从而其两端壳体边缘效应互相耦合的结构,其塑性破坏机构大多属于图3 中的机构B,即锥壳两端与大、小圆柱壳连接处及大、小圆柱壳中出现塑性铰,三个元件同时发生塑性流动的情况,此时对应的kII=SII/Sm可能远小于1.1,按弹性名义应力分类的准则无法适用。
本文给出了是否需要考虑锥壳两端边缘效应耦合的判据,见表4。
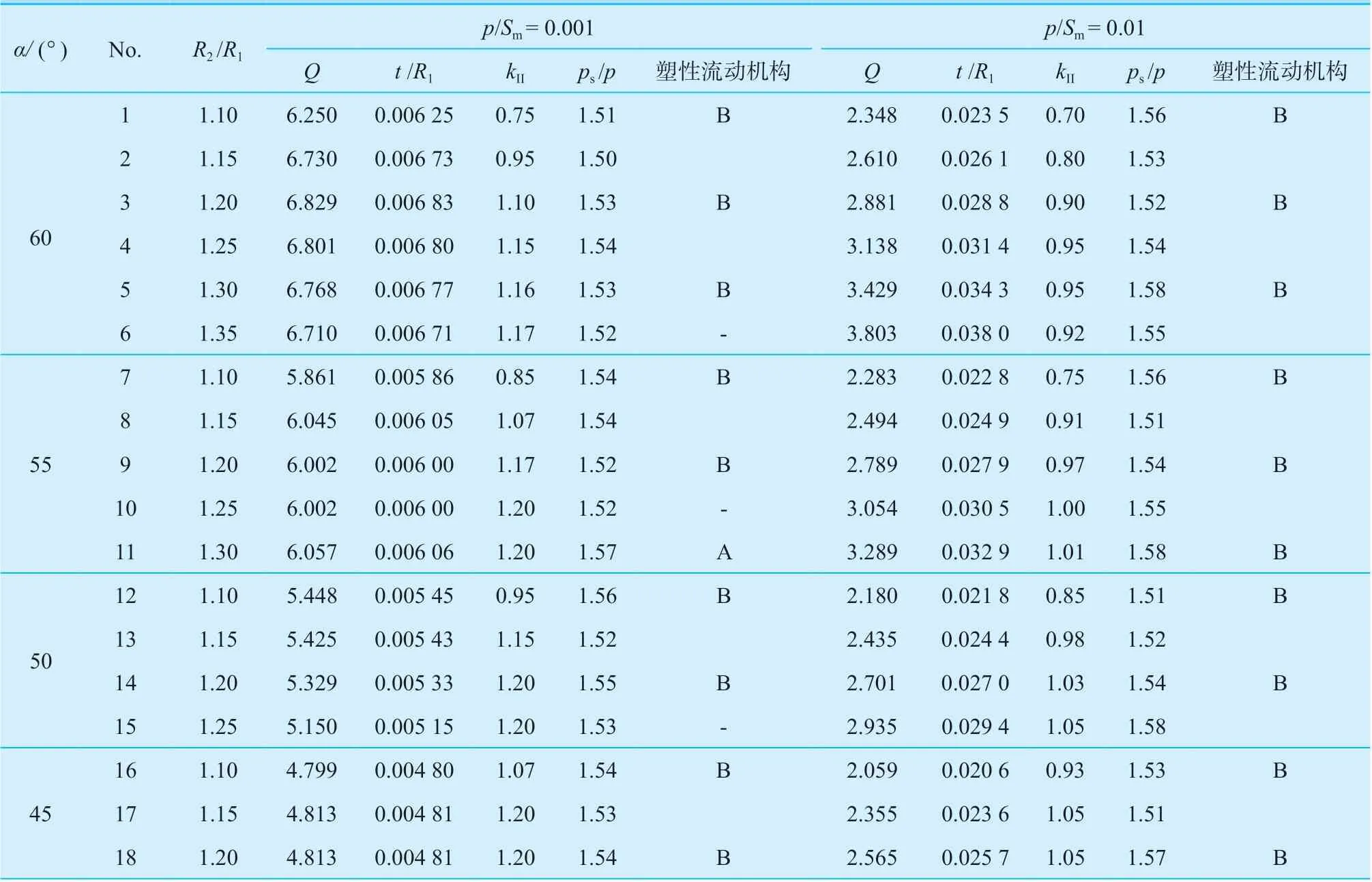
表3 短锥壳变径段两端边缘效应耦合结构的塑性极限载荷Table 3 The plastic limit pressure of short conical reducer in boundary effect conjunction of two end intersections

表4 锥壳两端边缘效应耦合的判定Table 4 Determination for the boundary effect conjunction of the two end intersections of conical reducer
7 结束语
清华大学课题组根据弹性薄壳理论的精确解和塑性极限分析,对锥壳与圆筒连接的无折边加强段提出了更加合理的分析设计方法,将适用范围扩大至α≤60°、p/Sm≥0.001,并提出了考虑锥壳两端边缘效应耦合的短锥壳变径段设计方法。
