均匀带电圆环电势的空间分布
2020-11-08罗志娟何艳喻莉
罗志娟 何艳 喻莉
(空军预警学院基础部 湖北 武汉 430019)
1 引言
均匀带电圆环是电磁学理论及应用中的基本模型,根据电势的叠加非常方便地计算其轴线上任意点的电势,但是对于空间任意点的电势,数学处理上有一定的困难,文献[1]利用MATLAB计算均匀带电圆环在空间任意点的电势分布,文献[2]利用第一类全椭圆积分计算了均匀带电圆环电势的空间分布,文献[3]利用椭圆积分和数学软件对均匀带电圆环电势和电场进行了研究.
本文避开复杂的数学积分计算,利用分离变量法和δ函数性质得出均匀圆环的空间电势分布的函数表达式,将轴线和圆心处对应的参数代入表达式中,得出轴线和圆心处的电势,与电磁学的结论一致,在利用分离变量中主要利用物理的边界条件,从而加深了学生对物理边界问题的理解.
2 均匀带电圆环在空间任意点的电势表达式
有一均匀带电细圆环,半径为a,总电荷量为Q,取球坐标系,坐标原点在环心,而圆环则处在赤道面上,如图1所示,分析得出除了圆环上各点外,电势处处满足拉普拉斯方程,并且空间任意一点(r,θ,φ)的电势u与φ无关.
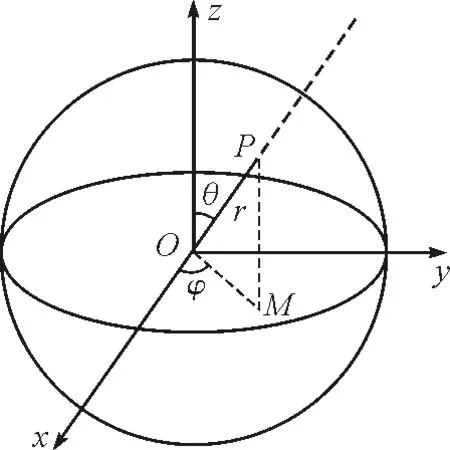
图1 球坐标系下的均匀带电圆环
设电荷密度分布函数为ρ(r,θ),则
常数C由圆环上的总电荷求出
则
可以写出电势u所满足的定解问题
(1)
|u|θ=0有界 |u|θ=π有界
(2)
|u|r=0有界 |u|r→∞→0
(3)
由δ函数的性质可知,当r≠a时,式(1)退化为拉普拉斯方程,这样,再由分离变量法结合式(2)和式(3)的边界条件,可以得到
(4)
考虑到δ函数应该是间断函数的导数,所以电势在球面r=a上一定是连续的
(5)
由式(4)、(5)可得
Alal=Bla-l-1
(6)

(7)
将δ函数也按勒让德多项式展开有
(8)
由式(4)、(7)和(8)得
(9)
因为
P2l+1(0)=0
所以
(10)
从结果中只含有偶次勒让德多项式,反映了静电势在赤道面反射不变性,即
u(r,θ)=u(r,π-θ)
3 带电圆环轴线上的电势
轴线上取式(10)中
θ=0
P2l(cosθ)=P2l(1)=1
代入式(10)得以下结论.
当r 当r>a时 合并上面的结论,则在轴线上的电势为 在圆心处取式(10)中 r=0 则式(10)中求和项只剩下l=0 P2l(0)=P2l(cosθ)=1 该结论与电磁学中讨论的结果是一致的. 本文主要利用分离变量法求出带电圆环在空间任意点的电势,避免了复杂的积分过程,在利用分离变量的过程中主要是利用物理问题的本质边界条件的应用,这样能加深学生对边界条件的理解.4 结束语
