基于Makkonen结冰增长模型的风力机覆冰预报

李仲怡，叶庚姣，卢小凤，李勇，唐百川

(1.广西壮族自治区气象灾害防御技术中心，广西 南宁 530022；2. 广西壮族自治区气象服务中心，广西 南宁 530022；3.南宁海关缉私局，广西 南宁 530022)

随着风力发电技术日趋成熟，风能已成为具有开发潜力和竞争优势的新能源，近十年来得到了前所未有的关注和飞跃式发展。广西风能资源较丰富，但是气象灾害频发[1]。大部分风电场建设在高山丘陵地区，冬季气温较低、湿度大，极易发生覆冰灾害且持续时间较长，风力机覆冰后会影响输出功率，而且冰块脱落可能造成安全事故[2-6]，严重的覆冰过程使风力机大面积停机，影响风电场经济效益；因此，风电场对风力机覆冰起止时间和覆冰厚度的预报有迫切需求，以便于电场调度安排生产和提前采取防灾措施。

由于发生载体不同，风力机覆冰与电线覆冰有本质区别。电线覆冰需超过承载负重才会影响输电安全，而风力机一旦发生覆冰就会有影响，严重时甚至会持续一个月不能发电，因此需要区别对待，开展具有针对性的研究。国内外有大量关于电线覆冰的研究，其中Makkonen结冰增长模型是最典型且运用最为广泛的模型之一[7]。Makkonen等于2000年提出电线覆冰模型，2001年将该模型应用于风力机覆冰模拟，研究了积冰模型对气象变量的敏感性，并将模型预报结果与冰风洞覆冰试验结果进行比较，结果应用于指导风力机叶片防冰加热元件设计[8-11]。国内有大量运用Makkonen结冰增长模型开展电线覆冰的研究[12-14]，而关于风电场风力机覆冰的研究却较少。由于缺乏有效的风电场风力机叶片覆冰厚度观测数据，目前风力机覆冰的研究大多是基于结冰增长模型的仿真结果与冰风洞覆冰试验结果来探讨风力机结冰的影响因子[15-19]。受人工模型试验条件限制，覆冰起止时间和厚度测量值存在误差，较难应用于风电场风力机覆冰预报，因此开展实地风力机覆冰研究并建立本地化风力机覆冰预报模型对风电场有极大的应用价值。

结合实际风力机覆冰资料和欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)模式预报资料，本文基于Makkonen结冰增长模型，首次以桂北风电场为研究对象对模型进行优化，建立了广西风力机覆冰预报模型，运用该模型对典型覆冰过程进行预报，并与实际风力机组覆冰起止时间比较，进行效果检验。

1 资料和方法

1.1 资料来源

数值模拟资料由ECMWF模式格点插值到风电场，ECMWF模式格点分辨率为12.5 km，时间分辨率为3 h，取前一日北京时间20时起报的未来72 h的预报数据驱动模型，预报要素包括降雨、气温、湿度、风速、气压等。气象要素实况资料为风电场附近自动气象观测站数据，桂北2个风电场(风电场A和风电场B)提供风力机的覆冰起止时间、风力机参数等资料。

1.2 数据处理

2018年11月28日至2019年2月28日，桂北风电场A、B气温在0 ℃以下共有67个时次，其中ECMWF模式预报正确的只有47个时次。由于ECMWF模式对山区的气温预报误差相对较大，通过与附近的自动站实况数据对比，采用线性回归分析方法，得出实况气温和预报气温的关系，如式(1)；另外根据经验，风电场A(B)气温预报值分别在1～3.2(3.8)℃、0～1.0 ℃时，实际气温已经分别在-1～0 ℃、-2～-1℃，因此对模式气温作式(2)的订正。

{ti}℃=1.139+0.867 3{Ti}℃.

(1)

(2)

式(1)、(2)中：Ti为逐3 h气温预报值；ti为订正以后的气温；风电场A的m取3.2 ℃，风电场B的m取3.8 ℃。

采用式(1)订正ECMWF模式气温预报数据，气温平均绝对误差降低了2.9%，0 ℃以下气温预报正确时次为30个，0 ℃以下气温平均绝对误差反而增加了63.8%；采用式(2)订正ECMWF模式气温预报数据，气温平均绝对误差增加了9.6%，0 ℃以下气温预报正确时次为65个，0 ℃以下气温平均绝对误差降低了23.9%。2019年1月风电场A的ECMWF模式气温订正结果如图1所示，采用经验公式对0 ℃以下气温订正效果较好的有221—224时次、282—283时次、312—317时次等。

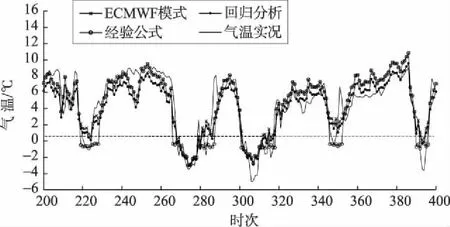
图1 2019年1月风电场A逐3 h气温曲线Fig.1 3 h temperature curves of wind farm A in January, 2019

总体来看，回归分析方法对整体的气温订正效果较好，但是对0 ℃以下气温订正效果较差，而风力机覆冰预报模型对低温预报准确率要求较高，由于经验公式对0 ℃以下气温订正效果较好，因此择优选择式(2)对模式气温进行订正处理。

1.3 结冰模型

由于本文侧重研究积冰起止时间预报，不涉及冰形状模拟，因此采用Makkonen结冰增长模型。覆冰过程主要由过冷却水滴的碰撞、捕获和冻结3个阶段组成，积冰质量增长率表达式为

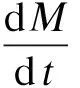
(3)

式中：M为积冰质量；α1为过冷却水滴的碰撞系数；α2为捕获系数；α3为冻结系数；w为粒子群含水量(质量分数)；v为有效粒子速度(即粒子相对于风力机的速度)；A为水滴碰撞物体有效截面积；t为时间。

α1采用较常用的Finstad等[20]的计算方法：

其中，NFsys为电路的整体噪声系数，NF1为第一级放大器的噪声系数，G1为第一级放大器的增益，NF2为第二级放大器的噪声系数。因为在实际的电路设计中，第一级放大器的设计对整体电路的噪声系数影响最大，需要尽可能的降低第一级放大器的噪声系数，同时提高第一级放大电路的增益，从而改善整体电路的噪声特性。

(4)

式中：K=ρWd2v/9μD，φ=Re2/K；Re=ρadv/μ，K、φ量纲为一，Re为雷诺数；ρw为水密度，取1.0×103kg/m3；ρa为空气密度，取1.293 kg/m3；v为相对风速；μ为空气绝对黏度，取1.798 4×10-5kg/(ms)。D为电线直径，Neil Davis等[21]以1 cm为桨叶厚度，模拟时假设直径取0.144 cm圆柱体进行模拟；d为液滴直径，Finstad等[20]认为不用计算每个液滴直径，只要知道中值体积直径(median volume diameter，MVD)即可，周悦等[18]对其值dMV的估算方法为dMV=(3.672+μ1)/γ，其中普型参数μ1=min{15,1 000/Nc+2}，斜率﹝wWC为液态水含量(质量分数)﹞，粒子总数浓度Nc取100 cm-3；Γ为伽马函数。

α2采用Admirat等人提出的经验公式：

(5)

对于冻结系数的计算，一般考虑干增长和湿增长。干增长时，所有被捕获的液滴全部冻结在物体表面，α3=1；对于湿增长，被捕获的液滴有部分没有立即冻结，并且在积冰表面发生的热传递过程中有部分积冰融化成为液态水，此时冰面热平衡公式为

Qf+Qv=Qc+Qe+Ql+Qs.

(6)

式中：Qf为水滴冻结释放的潜热；Qv为气流与冰面摩擦产生的热；Qc为气流带走的热感；Qe为冰面蒸发损失的热；Ql为加热过冷水滴到冰点损失的热；Qs为短波辐射和长波辐射产生的热。Makkonen等[8]通过解此方程，得到

(7)

式中：F=α1α2wv；E为表面未冻结部分(即液态水部分)占比，取0.3；h=Nu·λa/D，其中努塞尔数Nu采用谢真珍等[14]的计算方法，Nu=0.032Re0.85，空气导热系数λa=2.536 2×10-5J/(m·s·K)；σ为斯蒂芬波尔兹曼常数，取5.669 6×10-8W/(m2·K4)；a为辐射常数，取8.1×107K3；ε为水汽的摩尔分子比(即干空气的分子质量与水蒸气的分子质量的比值)，取0.62；p为气压，取实况值；ts、ta、td分别为冰面温度、气温、液滴碰撞温度，对于纯水ts=0，对于云中积冰和冻雨结冰td=ta；水气压pa=p0kh/100，当T>0 ℃时{p0}Pa=611exp[17.27{T}℃/({T}℃+237.3)]，当T≤0 ℃时{p0}Pa=611exp[21.87{T}℃/({T}℃+265.5)]；k为电线表面局部恢复系数，取0.79；ps为饱和水气压，取6.17 Pa；水冻结潜热Lf、蒸发潜热Le分别取3.34×105J/(kg·K)、2.501×106J/(kg·K)；空气比热Cp、水的比热Cw分别取1 004.07 J/(kg·K)、4 218 J/(kg·K)。

相对风速v采用Virk等[18]的计算方法，液态水含量wWC采用文献[12]的计算方法，表达式为：

(8)

(9)

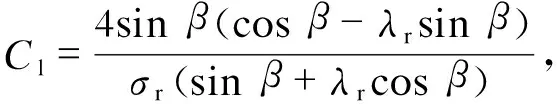
2 模型优化

2.1 相对风速公式优化

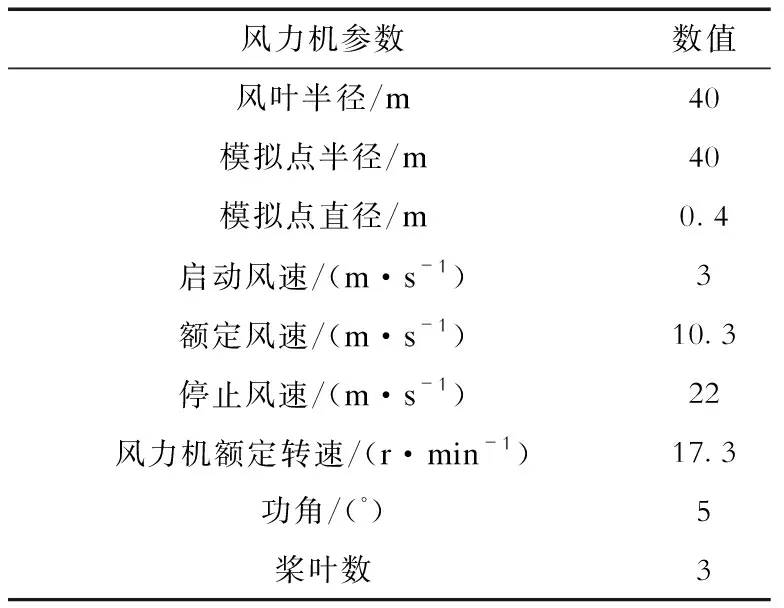
表1 GW82/1500风力机参数Tab.1 Parameters of GW82/1500 wind tubine

(10)

式中vf,i为逐3 h自然风速，i表示采样点。当气温大于0 ℃时，不同自然风速下对应桨叶叶尖水汽粒子的相对风速如图2所示。

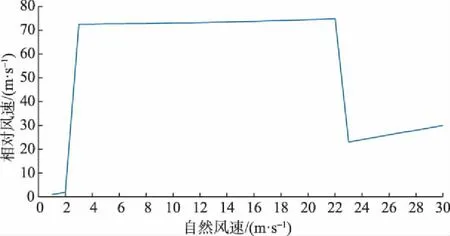
图2 气温大于0 ℃时相对风速与自然风速的关系曲线Fig.2 Relationship curve between relative wind speed and natural wind speed when the temperature is greater than 0 ℃

2.2 建立融冰影响因子

太阳辐射是影响风力机融冰的重要因素，但是ECMWF数值预报没有这个要素，且风电场附近也缺乏太阳辐射的实况数据，而液态水含量能间接影响融冰，因此本文通过控制液态水含量来建立融冰影响因子。

当有降雨时，液态水含量wWC采用文献[12]的计算方法，根据经验当数值预报累计12 h无降水，并且预报气温大于0时，有利于融冰，液态水含量为0；当不能满足较长时间无降水或气温低于0 ℃时，考虑空气仍较湿润，相对不利于融冰，液态水含量取0.1。表达式为：

(11)

式中TPi为降水预报值。

2.3 敏感性分析

影响风力机覆冰的外部因素是风力机的参数(见表1)，而内在影响因素有降水、相对湿度、气温、风速、气压、液态水含量等。为了验证该模型在桂北风电机组的适用性，下面将针对气温、降水、风速进行敏感性分析。敏感性分析方案见表2，为方便分析把最大积冰厚度设置为100 mm。

表2 敏感性分析方案Tab.2 Sensitivity analysis schemes

气温、降水、风速影响覆冰厚度变化的曲线如图3所示。图3(a)所示为方案1，气温越低覆冰增长越快；随着气温降低，相同的降温幅度下，覆冰增长率的变化减小。图3(b)所示为方案2，可见降水量越大，即液态水含量越高，覆冰速率越快。图3(c)所示为方案3，随着风速的增大，覆冰增长反而越慢，因为相对风速的增加会增大碰撞系数，但是翼型表面的热力学平衡过程有2个对立影响：一是风速增大物体表面的对流散热，利于覆冰量增加；二是风速增大，物体表面摩擦生热以及水滴动能增大，利于覆冰量减少[16]。因此当风速在适宜范围内时，覆冰增长速度才较大。

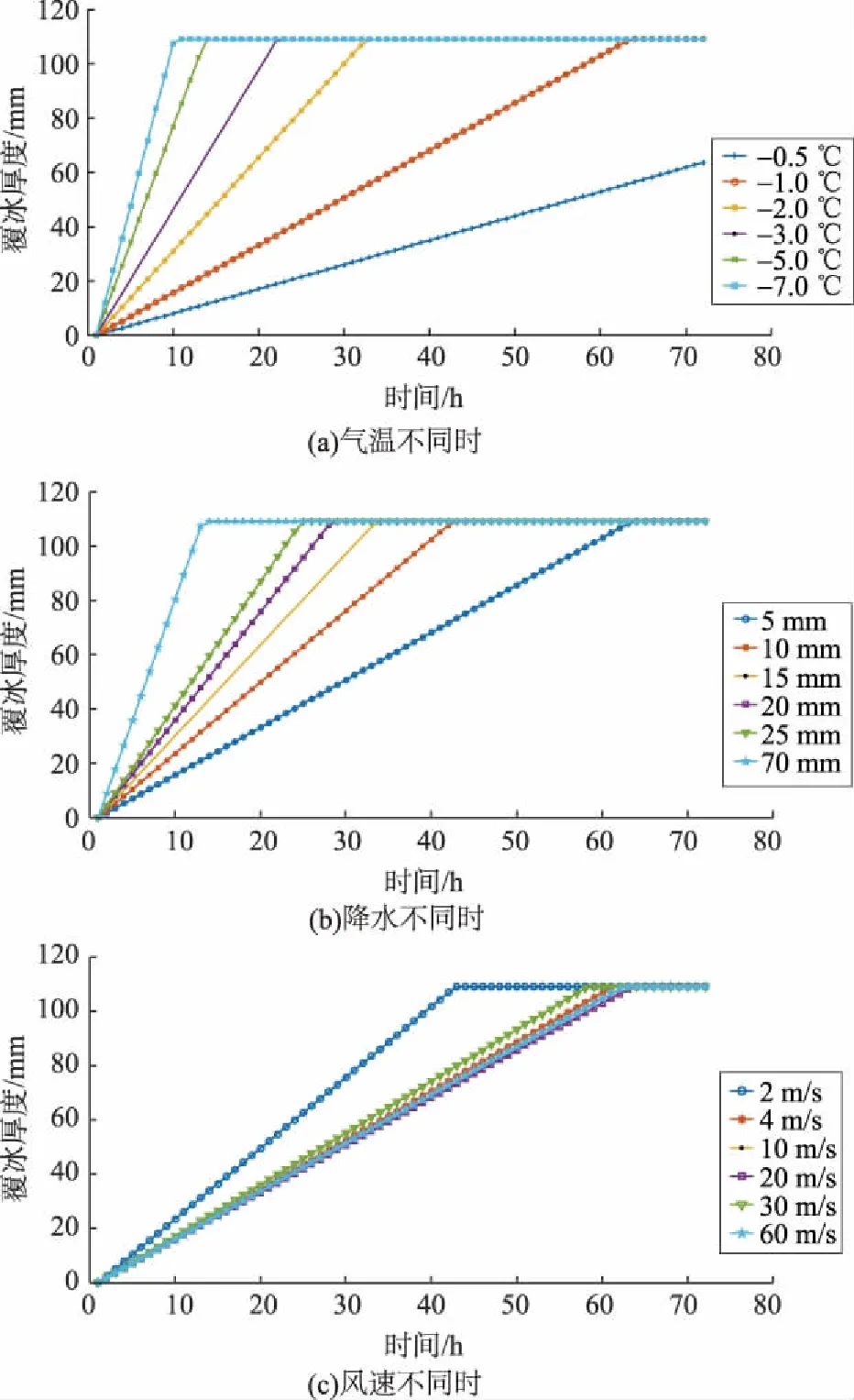
图3 不同条件下覆冰厚度变化曲线Fig.3 Variation curves of icing thickness of wind turbine under different conditions

3 2019年冬季覆冰预报检验

将ECWMF气象预报模式的降水、相对湿度、气温、风速、气压等资料代入建立的风力机覆冰预报模型，对桂北风电场A、B2019年11月1日至2020年3月31日的覆冰过程进行逐日预报，其中风电场A、B分别有66台、340台风力机，预报检验结果见表3、表4。覆冰停机时间指的是由覆冰引起的第1台风力机停机的时间；融冰开机时间指风力机全部融冰并正常运行的时间；覆冰过程报出率是指风电场风力机覆冰起止时间不漏报的概率。

由表3可见，风电场A共8次过程，提前24 h、48 h、72 h覆冰过程报出率分别为100%、100%、75%。提前24 h、48 h、72 h覆冰开始时间预报的平均绝对误差分别是3.8 h、4.1 h、3.7 h，预报误差小于5 h的过程占比分别为75%、75%、83%，预报误差小于2 h的过程占比分别为38%、25%、17%。风电场A融冰开机时间受金中旺线输电线路融冰影响，第5次过程的覆冰结束预报时间误差较大，因此剔除异常偏大过程，提前24 h、48 h、72 h预报的覆冰结束时间平均绝对误差分别是7.8 h、7.8 h、13.2 h，预报误差小于5 h的过程占比分别为29%、43%、14%，预报误差小于2 h的过程占比分别为29%、43%、14%。

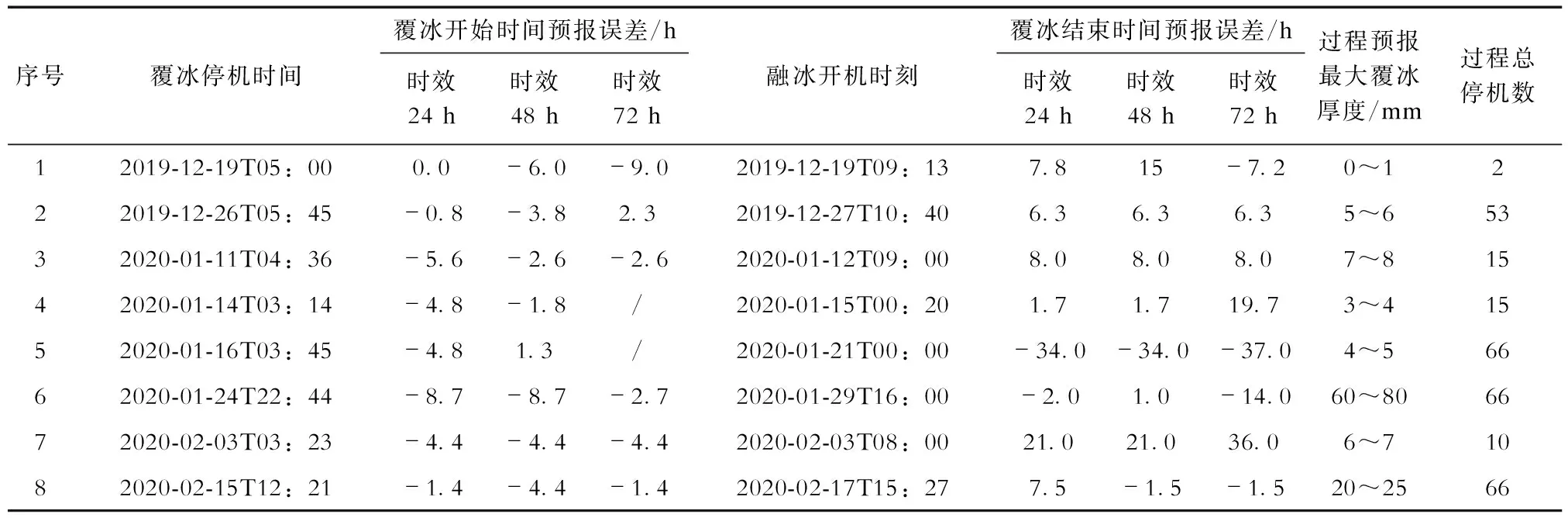
表3 风电场A风力机覆冰预报检验结果Tab.3 Test results of wind turbine icing prediction in wind farm A

由表4可见，风电场B共9次过程，提前24 h、48 h、72 h覆冰过程报出率分别为100%、100%、67%。提前24 h、48 h、72 h预报的覆冰开始时间平均绝对误差分别是4.8 h、4.7 h、5.6 h，预报误差小于5 h的过程占比分别为67%、78%、67%，预报误差小于2 h的过程占比分别为33%、44%、50%。风电场B提前24 h、48 h、72 h预报的覆冰结束时间平均绝对误差分别是6.1 h、11.6 h、11.7 h，预报误差小于5 h的过程占比分别为67%、44%、43%，预报误差小于2 h的过程占比分别为44%、11%、29%。

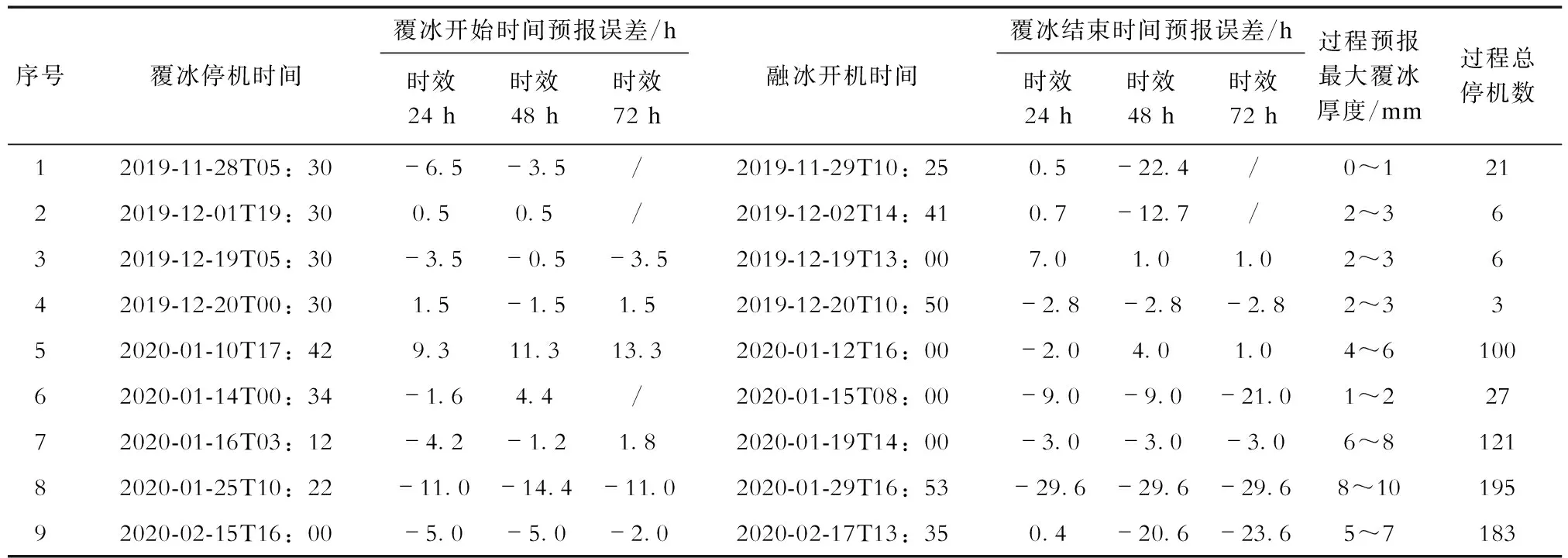
表4 风电场B风力机覆冰预报检验结果Tab.4 Test results of wind turbine icing prediction in wind farm B

总体来看，风电场预报覆冰开始时间早于实际停机时间，融冰开机时间反之，因为风力机可能达到一定覆冰厚度后才会出现输出功率异常或直接停机的情况，据统计覆冰停机时覆冰厚度为0.5～1 mm。预报的覆冰厚度越大，覆冰时间越长，风电机组停机台数越多；因此，可以根据模型预报的覆冰厚度和时长来预判覆冰过程强度，预估停机数量。另外，风力机覆冰厚度较小时，可能恢复正常运转，据统计融冰开机时覆冰厚度为0.5～2 mm。如表3中序号1过程，风力机停机时间仅4.2 h，风力机仅停机2台，这种覆冰时间短、过程强度较小的风力机覆冰过程误差相对较大，原因可能是ECWMF模式对较弱降温过程的气温预报误差较大。

从以上预报结果可以看出提前48～72 h的风力机覆冰过程预报结果与实际覆冰情况相近，预报风力机覆冰起止时间大致相符，能为风电场合理安排生产和采取防灾措施提供有效的参考。

4 结论

本文基于Makkonen结冰增长模型，通过优化模型和气象因子敏感性分析，建立了风力机覆冰预报模型，采用优化的风力机覆冰预报模型对桂北风电场A、B 2019年11月1日至2020年3月31日期间的覆冰过程进行了预报和检验，结论如下：

a)通过订正气象数值预报的气温值、优化相对风速计算方法和建立融冰影响因子，使风力机覆冰预报模型更符合风力机运行和覆冰特点，以提高适用性和预报准确率。

b)敏感性分析结果表明，在适宜的风速下，温度越低，降水越大，覆冰增长越快，符合覆冰物理变化规律。

c)该模型对风电机组覆冰时间预报具备预报时效长、预报准确率高的特点。48 h时效内覆冰过程报出率为100%，覆冰起止时间预报误差分别为3～5 h、6～12 h；72 h时效内风力机覆冰预报效果较稳定，65%以上的覆冰开始时间预报误差可控制在5 h内。风电场可以根据预报的覆冰起止时间、覆冰时长和覆冰厚度等预判覆冰过程强度，提前48～72 h安排生产和提前启动防灾预案。

风力机结冰对风电场经济和安全造成严重影响，本文基于Makkonen结冰增长模型，建立了风力机覆冰预报模型，研究结果可对整个风电场或者分区结冰提供预报参考。由于缺乏风电场风力机覆冰厚度观测数据，目前风力机覆冰模型的厚度预报无法检验。本文模型预报的过程最大覆冰厚度大小与覆冰造成的停机数量有较好的对应关系，在今后的研究中，可以根据覆冰过程停机情况和覆冰厚度建立关系，表征覆冰过程强度，或者在风电场搭建风力机叶片覆冰观测设备。驱动模式ECWMF模式分辨率为12.5 km，针对单台风力机的预报，还需要引进更高分辨率的预报模式，以提高预报精细化程度。