基于TRIZ发明原理的水轮发电机组优化设计

王旭 陈荣盛 卢磊

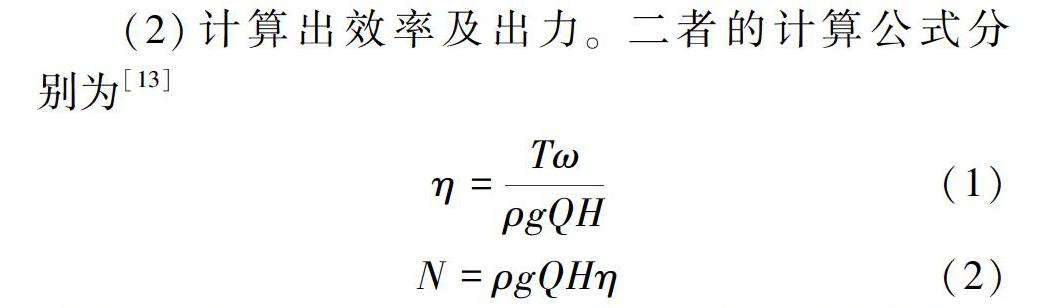
摘 要：为解决水轮发电机组在优化设计中出现的技术矛盾，改善机组的各项性能，在对某混流式水轮发电机组进行优化设计时，为解决机组堵塞严重的问题，同时让机组在优化设计前后流场、效率以及出力等参数基本保持在设计值，提出了减少叶片数量的方案，分析了减少叶片数量会导致恶化的参数类型，以TRIZ发明原理的推荐方案为指导原则构建技术矛盾关系，并提出了降低活动导叶高度和增大叶片表面积等优化措施，对全流道进行CFD数值计算和现场实测两个方面验证改造效果。结果显示，改造后机组的流态良好，堵塞频率显著下降，且效率和出力均达到了预期水平，为后续机组的进一步优化设计提供了参考依据。

关键词：TRIZ发明原理;水轮发电机组;优化设计;技术矛盾;CFD数值计算

中图分类号：TV136 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.10.032

Optimum Design of Francis Turbine Based the Principle in TRIZ

WANG Xu1， CHEN Rongsheng2， LU Lei3

（1.Chengdu College of University of Electronic Science and Technology of China， Chengdu 611731， China;

2.Chengdu Hydroelectric Investigation & Design Institute of SPC， Chengdu 610000， China;

3.Yingxiuwan General Hydropower Plant， Dujiangyan 611830， China）

Abstract：The primary goal of this research was to solve the technical contradiction in the process of Francis turbine optimum design. The paper took the Francis turbine as an example， in order to solve the problem of serious congestion and keep the good performance of turbine. We proposed to reduce the number of blades and analyzed to reduce the number of blade that could lead some parameters deterioration. And then the paper built the conflict matrix based the TRIZ. According to the guiding principles of TRIZ， we used the lower height guide vanes and enlarged blade area. At last， we did the simulation by CFD and site tests for verified the effectiveness and output. In conclusion， the results show that the improved turbine has a good performance. It has provided a reference for the future optimum design.

Key words： principle in TRIZ; francis turbine; optimum design; technical contradiction; CFD analysis

对于一些运行时间较长的中小型水电站，由于水轮发电机组转轮选型不当、零部件设备老化等因素，容易导致流道堵塞、效率下降和出力降低等问题，影响电站的经济效益[1]，因此对水轮发电机组进行合理的优化设计，在改善其性能、提升发电效率以及经济效益等方面有举足轻重的意义。

有关水轮发电机组优化设计的研究结果表明，采用单一措施改善机组某些性能参数时，往往会导致另一些参数的恶化。例如：当叶片包角增大时，机组出力能够得到有效提升，但同时机组却容易偏离最优工况，其效率会有所下降[2];当叶片表面积增大时，转轮的抗汽蚀性能和强度均会得到改善，但比转速会降低[3];当叶片数量减少时，转轮的过流量会显著增大，但机组的汽蝕程度会加剧[4]。由此可见，在机组的优化设计中，改善参数和恶化参数同时存在，即二者构成了技术矛盾。鉴于此，为避免恶化参数影响机组的整体性能，有效解决技术矛盾，笔者在对某电站混流式发电机组进行优化设计时，采用了基于技术矛盾的解决理论——TRIZ发明原理[5]，并根据其指导原则，提出优化设计方案，达到预期目标。

1 工程问题描述

以某水电站混流式水轮发电机组为优化设计对象，该机组投入使用至今已近20 a。由于转轮选型不当，机组自投入运行以来流道经常堵塞，导致停机时间长、运行效率低和稳定性差等问题，因此需要对该机组进行优化改造，解决流道堵塞问题，提升其工作性能，将出力、效率等各项参数恢复至原始设计的状态。原机组的部分参数见表1。

2 基于TRIZ发明原理的水轮机优化设计

TRIZ发明原理是一种基于技术矛盾的解决理论。该原理是在工程问题解决方案统计学基础上，发掘设计对象的技术矛盾，并通过推荐方案减轻或解决该矛盾，最终得到设计的理想解[6]。在对混流式水轮机进行优化设计时，需要减轻或消除某个不利因素，然而，对该因素的改善会导致其余因素恶化，此时就构成了技术矛盾。因此，采用TRIZ发明原理的目的就是解决该技术矛盾，实现合理的优化设计。具体流程如图1所示。

2.1 技术矛盾关系的建立

由上述分析可知，该机组的主要问题在于转轮选型不当造成流道堵塞，从而引起机组的其他性能问题。因此，如何消除流道堵塞，是优化设计的关键因素。通常而言，采用减少叶片来增大转轮开口是最行之有效的措施。然而，叶片的减少会增大水流的出口环量，导致机组效率下降;同时，由于叶片数减少后，其周向力、水力矩均会增大，因此在其余条件不变的前提下，转轮强度会降低[7]。故消除流道堵塞与效率、强度构成了技术矛盾。

由于TRIZ发明原理中定义了39个通用工程参数，因此需要将水轮机的技术矛盾因素转换成对应的通用工程参数[8]。通过减少叶片来消除堵塞的措施，主要是为了使过流量增加，而水流是处于运动状态的，过流量增加则意味着流过转轮的体积增加。因此，该因素转换成的通用工程参数为运动对象的体积。 同理，分别将效率和强度转换为对应的通用工程参数能量损失、强度。

上述构成矛盾的通用工程参数及TRIZ发明原理中推荐的解决方案见表2。

2.2 优化设计方案的确定

根据表2中的解决矛盾推荐方案，进行机组的优化设计方案分析和选择。以能量损失为例，在水轮发电机组优化设计中，具体的矛盾为：叶片数量的减少增大了转轮开口及流量（即改善参数为运动对象的体积），但与此同时机组效率下降（能量损失加大）。因此，为解决该矛盾，表2中列出的TRIZ发明原理推荐方案包括7、15、13和16。发明原理7是将机组的某一个过流部件通过另一个过流部件的空腔来实现，而水轮发电机组的过流部件具有固定的配合关系，故该方案无法实现;发明原理16是通过改善转轮叶片的工艺和翼型等措施降低矛盾程度，即适当减轻效率的下降程度，但由于该机组的改造目标是在不降低效率的前提下减轻流道的堵塞，故该方案也不予考虑。发明原理15的指导原则为调整机组的过流部件，使内部流场状态改善，其性能得到优化，即在保持经济性的前提下，不局限于转轮，可以对任意过流部件进行结构改进;发明原理13，即采取逆转措施来解决由于增大转轮出口而产生的恶化因素。综上所述，优化设计方案推荐的可行发明原理为15和13，具体措施是：减少叶片数量，该措施会有效改善机组堵塞的问题，但水流流过叶片的过流量会增加，致使最优工况向大流量区偏移，故必须调整流场动态性能，防止效率降低。采取利用适当降低活动导叶高度的措施来反向调整过流量（发明原理13），既能解决堵塞的问题，又消除了机组最优工况向大流量区偏移的现象（發明原理15），确保效率不下降。按照上述方法，改善机组结构强度性能的措施见表3。

根据表3中的优化设计方案，具体设计中，转轮直径保持不变，叶片数目按照比转速进行确定，故将叶片数调整为14片，此时叶片平均开口将显著增大，由改造前的21 mm增至30 mm;而导叶高度降低的程度，按照比转速及水头损失最小原则确定[8]，因此导叶相对高度由优化设计前的0.225降低至0.200;转轮设计按照文献[9]的流程进行，新旧转轮轴向流道对比见图2。

3 CFD数值计算及现场测试

机组的优化设计完成后，需要验证其内部流场的特征，以判断水流的流态是否满足要求。笔者采用CFD对机组进行流场模拟，数值计算对象为优化设计后的机组全流道。

3.1 条件设置

在CFD分析前，对模型进行条件设置，主要流程如下。

（1）网格划分。分别对主要过流部件蜗壳、导水机构、转轮及尾水管划分网格，网格类型均采用TGrid，并进行拼接[10]。

（2）定义边界条件。将蜗壳的进口截面设置为压力进口边界，尾水管出口截面设置为压力出口边界[10]。

（3）湍流模型的选择。在定常流动中，湍流是不均匀的，受机组内部过流部件形状的影响，水流呈曲线轨迹，因此RNG k-ε湍流模型的适应性较好[11]，故湍流模型确定为RNG k-ε模型。

3.2 计算结果的后处理

对额定水头下导叶开度为70%、80%、85%、90%和100%的5个工况点进行仿真，以85%开度为例进行计算结果后处理分析。

3.2.1 流场特征分析

导水机构流场状态如图3所示，从进水端至出水端，水流速度呈增大的趋势，且整个流线比较顺畅。无论是固定导叶进水端还是活动导叶出水端，都未发生明显的脱流和旋涡等现象。从压力的分布情况来看，沿进水端至出水端逐渐降低，也表现出均匀变化的规律。整体而言，速度与压力均沿导水机构的周向对称，表明流态情况良好。由此说明，降低相对高度后的活动导叶与转轮配合情况较好。

新转轮叶片的压力分布情况如图4所示，从叶片的进水边到出水边，其正面和背面的压力基本表现为梯度均匀下降的规律。从负压范围来看，叶片正、背面进水边与下环配合处的极小区域存在负压，表明叶片抗汽蚀性能良好。转轮叶片速度分布情况如图5所示，水流比较流畅、整个转轮流场范围均未发生二次流动（回流、脱流和横向流），从进水边至出水边的速度逐渐增大，能量转换效果良好。

整个流道的速度分布如图6所示，水流从蜗壳进口至尾水管出口，整体的流动比较顺畅。蜗壳中的水流呈等速度矩分布的规律，起到了较好的引流效果，为导水机构和转轮的良好流态分布奠定了基础。当水流进入尾水管时，其速度矢量基本能够保持垂直向下，且尾水管的直锥管段内不存在偏心涡带，而普通涡带从尾水管的中段至末端逐渐减弱直至消失，符合尾水管内部的正常流动规律[12]。

综上所述，采用TRIZ发明原理完成优化设计后从机组内部流动特征来看，水流的动态特性良好，达到了预期的效果。

3.2.2 效率、出力预测及现场实测

优化设计后的机组效率和出力是否能够达到原设计参数，需要根据CFD分析结果进行预测。其中，效率预测的步骤为：

（1）根据各工况下的CFD计算结果，获得力矩、流量以及转速等参数值。

（2）计算出效率及出力。二者的计算公式分别为[13]

η=TωρgQH（1）

N=ρgQHη（2）

式中：η为效率;T为转矩;ω为发电机轴的旋转角速度;ρ为流体密度，即103 kg/m3;g为重力加速度，即9.8 m/s2;Q为流量;H为水头;N为出力。

按照上述步骤，在额定水头下，计算导叶开度为70%、80%、85%、90%和100%工况下的效率与出力值，并采用文献[14]的方法进行修正，获得了发电机出力值。同时，由于该优化措施已被电站实施，因此结合电站反馈数据情况，将效率及发电机出力的仿真和实测值进行对比，见图7、图8。

从图7可以看出，CFD仿真结果和现场实测效率的变化规律基本一致，二者均在导叶开度为85%时效率达到最高。但整体而言，各开度下的效率偏差均不是很大。受机械损失、容积损失等因素的影响，各开度下的现场实测值均比仿真值略低，但误差较小，除导叶100%全开外，效率基本上保持在87.5%～88.7%，基本满足要求。

从图8可以看出，现场发电机出力实测值比发电机出力计算值也略低，在各开度下，二者的偏差均在5%以内，属于合理的误差范围。同时，根据现场实测结果可知，当导叶开度为87%时，机组达到额定出力，而CFD分析预测达到额定值的开度为85%，故二者的结论基本一致。最后，以一个汛期为观察周期，统计发生堵塞的次数为3次，远低于优化前平均每天堵塞1次的频率。

综上所述，从机组的效率、出力和堵塞频率来看，采用TRIZ发明原理对机组进行优化设计，通过增大转轮开口解决堵塞问题的前提下，其余参数均保持在预期水平，最终的改造效果是比较良好的。

4 结 论

针对某电站混流式水轮发电机组运行中存在堵塞的问题进行优化设计，分析了机组改造中存在的技术矛盾，采用TRIZ发明原理从导叶高度降低、转轮叶片的设计等方面进行改造。从CFD分析及现场实测结果两个方面均体现出了该优化设计方案的合理性，同时堵塞的频率大幅下降，达到了预期的改造目标。

参考文献：

[1] 苏文良.水轮机转轮选型、制造和投运过程中问题处理[J].水电站机电技术，2004（5）：12-15.

[2] 苏博文.基于CFD三叶片贯流式水轮机转轮改型研究[D].西安：西安理工大学，2018：44-59.

[3] 郑源，陈德新. 水轮机[M].北京：中国水利水电出版社，2011：81-88.

[4] 王鑫. 6MW小型混流式水轮机过流部件匹配设计[D].西安：西安理工大学，2018：21-22.

[5] KAREN Gadd， CLIVE God. Triz for Engineers： Enabling Inventive Problem Solving[M]. New Jersey： Wiley，2011：22-42.

[6] PHILIPP Tursch，CHRISTINE Goldmann，RALF Woll.Integration of Triz Into Quality Function Deployment[J].Management and Production Engineering Review，2015，6（2）：56-62.

[7] 程良俊.水輪机[M].北京：机械工业出版社，1984：201-202.

[8] DMITRIY Bakhturin， NAUM Feygenson. Technical Platform & Basic Design： Challenge of New Engineering Phenomena（Towards Review of Ontological Basis of Classical TRIZ）[J].Procedia Engineering，2015（12）：682-688.

[9] 哈尔滨大机电研究所.水轮机设计手册[M].北京：机械工业出版社，1976：224-227.

[10] NICOLLE J， MORISSETTE J F， GIROUX A M. Transient CFD Simulation of a Francis Turbine Startup[C]//The 26th IAHR Symposium on Hydraulic Machinery and Systems. Beijing： China Academic Journal Electronic Publishing House，2012：1-8.

[11] 于晓丽，王树杰，袁鹏，等. 两种湍流模型在潮流能水轮机数值模拟中的适用性研究[J].中国海洋大学学报（自然科学版），2019，49（2）：114-120.

[12] 朱李，赵玺，赖喜德.基于CFD的混流式水轮机流动特性分析[J].水力发电，2015，41（6）：91-94.

[13] 王旭，张佳芬，卢婧，等.水轮机转轮叶片割边改造的CFD与模型试验分析[J].机械设计与制造，2017（1）：6-8.

[14] 宋文武.水力机械及工程设计[M].重庆：重庆大学出版社，2005：58-65.

【责任编辑 崔潇菡】