高填土软土桩基堤防加固的三维数值分析

2020-11-06王政平湛杰贾东远

人民黄河 2020年10期

王政平湛杰贾东远

摘要：为明确高填土软土桩基堤防变位机理，提出合适的加固方案，以梧州河东堤西江段为背景，对堤防及其基础进行数值分析。考虑超孔隙水压力，运用防洪堤-桩-地基三维流固耦合数值法，对参数进行敏感性分析和反演，发现堤防小变位时其变位由变形模量主导，大变位时由抗剪强度主导;地基参数建议值存在一定的富余;洪水漫顶时，堤防主体结构仍安全，但存在大应变区;各排桩受力存在较大差异;根据大应变区分布，提出充填灌浆加固方案;在设计洪水位时，加固后堤防变位减小显著，结构强度满足规范要求，表明加固方案有效可行。研究表明，数值分析是复杂堤防变位分析的有效手段，分析方法和加固方案可为类似工程提供参考。

关键词：高填土;桩基;堤防;加固;变位;数值分析

中图分类号：TV22;TV87 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.10.012

3D Numerical Analysis of Pile Foundation Embankment Reinforcement in High Fill Soft Soil Foundation

WANG Zhengping， ZHAN Jie， JIA Dongyuan

（China Water Resources Pearl River Planning Surveying & Designing Co.， Ltd.， Guangzhou 510610， China）

Abstract：In order to clarify the mechanism of embankment displacement of high-fill soft soil pile foundation， a suitable reinforcement scheme was proposed， based on the Xijiang section of the east embankment of Wuzhou River， the numerical analysis of the embankment and its foundation was carried out. Taking the pressure of excess pore water into account， the sensitivity analysis and inversion of the parameters were carried out by using the three-dimensional fluid-solid coupling numerical method of “levee-pile-foundation”. It found out that the variation of embankment was dominated by deformation modulus and shear strength when it was large. The suggested value of ground parameter had certain surplus. When the flood overtops， the main structure of the embankment was still safe， but there was a large strain zone. There were great differences in the forces of each pile row. According to the distribution of plastic area， the reinforcement scheme of filling and grouting was proposed. When the flood level was designed， the dike displacement after reinforcement was reduced and the structural strength met the standard requirements， which indicated that the reinforcement scheme was effective and feasible. It is shown that numerical analysis is an effective method to analyze the displacement of complex dyke.

Key words： high filling; pile foundation; embankment; reinforcement; displacement; numerical analysis

混凝土扶壁框架式防洪堤具有質量轻、占地少的优点，在城镇、江河等防洪工程中得到了广泛应用。这种结构遇到深厚淤泥或杂填土时，常采用混凝土桩基来提高地基承载力和控制竖向沉降[1]，而对桩基水平抗力和水平位移量的控制还存在许多困难，特别是堤防后存在高填土时，情况更加复杂。例如，桩基由多排桩组成时，各排桩相互影响，水平抗力存在较大差异;桩基承台侧面也受土压力时，桩基和承台抗力分载关系复杂[2-3];高填土自重对桩基产生侧向压力;地基软土在渗透压力下自身发生复杂的变形。

目前，对桩基的水平抗力计算，我国规范[4-5]推荐采用m法、K法、C法和P-Y曲线法等，但这些方法只适用于简单情况或单一受力模式，对复杂桩基的工作状态却不能正确反映，计算精度十分有限。

梧州市河东防洪堤西江段位于深厚杂填土之上，墙后为高填土。非汛期，外江水位较低，且远低于堤后填土高程，桩基主要抵抗高填土的土压力，形成水平向的静力平衡;汛期洪水上涨并超过堤后填土高程时，堤后土压力持续增大，而桩基水平抗力先减小，然后反向增大，堤后土压力和桩基水平抗力共同抵抗外江水压力。地基、防渗墙还受渗流场作用，受力复杂，在高填土软土桩基堤防中十分具有代表性。为了分析高填土软土桩基堤防的工作机理和变位特性，明确桩基各受力特点，以该工程为研究背景，基于三维流固耦合数学模型，分析堤防的受力和变形特性，并提出合理可靠的加固方案，为其他类似工程提供参考。

1 工程概况

梧州市河东防洪堤位于梧州市河东区桂江东岸和西江北岸，呈半圆状护卫河东城区，规划挡洪标准为50 a一遇，工程级别为2级，是重要城防工程，也是广西重点工程。工程包括桂江段和西江段，长度分别为1.76 km和1.82 km。

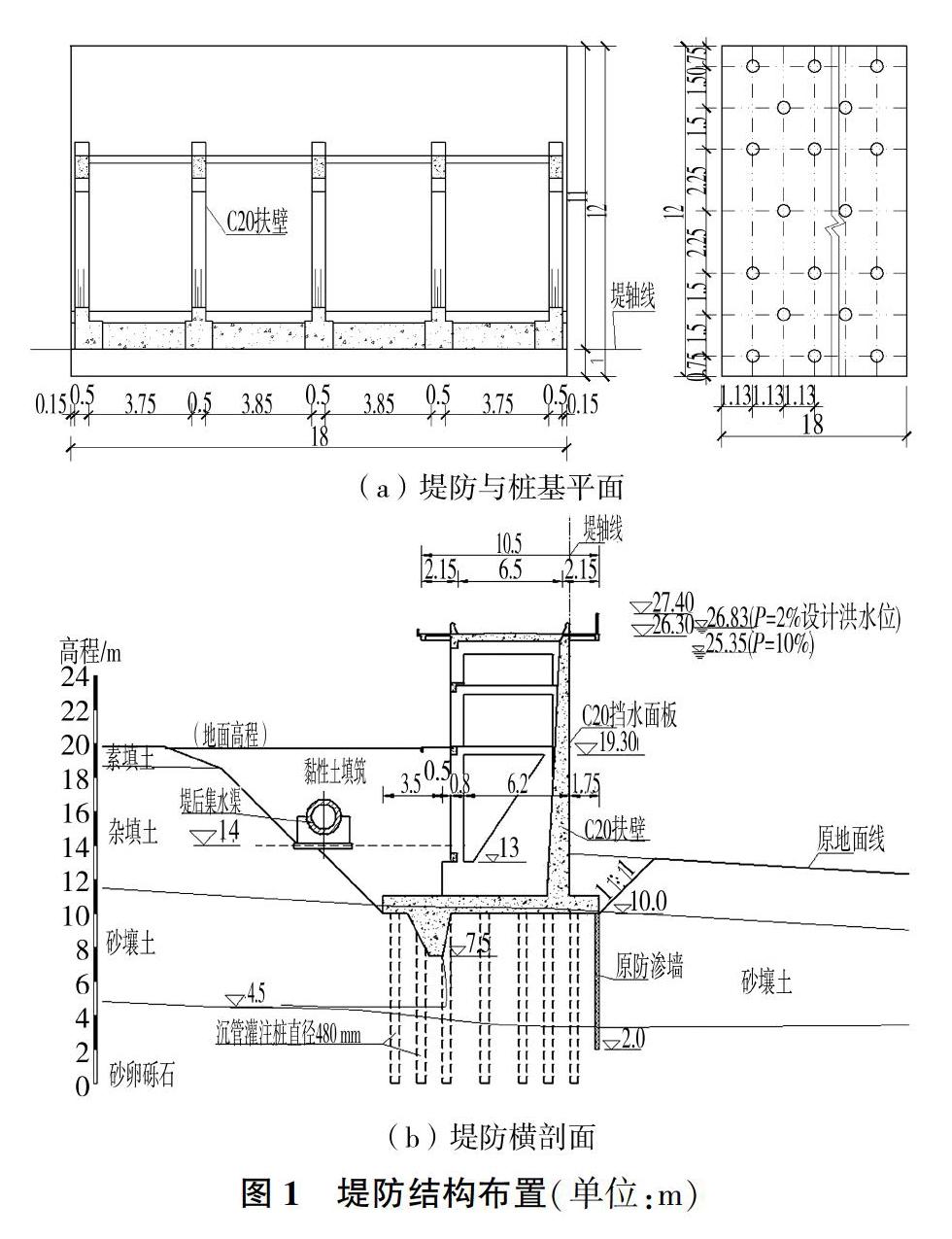
根据设计资料，西江堤堤基上层覆盖厚度8～10 m的杂填土，其下为厚5～7 m的砂壤土，再往下是砂卵砾石。堤身结构在堤内地面以下为扶壁式结构，地面以上为框架式结构。堤内地面高程20.0 m，堤顶高程26.3 m，堤顶宽10.5 m。防洪堤挡水板顶宽0.6 m，底宽1.4 m。承台厚1.0 m，宽12.0 m，长18.0 m。基础采用7排直径为0.48 m的沉管灌注桩，桩长9～25 m。防洪堤踵部设置阻滑齿墙，前趾设悬挂式防渗墙，深度7 m，防渗墙采用多头小直径深层搅拌水泥土墙。堤防结构布置如图1所示。人民黄河 2020年第10期

2005年，西江堤遭遇超标洪水而漫顶，发生大变位，并造成堤后设施起拱、破坏，存在安全隐患，需要进行除险加固方面的研究。

2 分析理论与解法

流固耦合的基本假定：①土完全饱和且各向同性;②固体颗粒和孔隙水可以压缩;③固体骨架的变形遵从Terzaghi有效应力原理;④孔隙水渗流服从Darcy定律;⑤土体在渗流过程中可发生位移;⑥土体孔隙率和渗透系数是动态变化的。

视土体为多孔介质，Terzaghi有效应力公式为

σ′ij=σij-αp（1）

式中：σ′ij为有效应力;σij为总应力;α为Boit系数，是0～1的一个常数;p为孔隙压力。

地基的渗流场和应力场相互影响，渗流场通过渗透压力和渗流体积力影响土体应力分布;应力场通过土体的体积应变及孔隙率影响渗透系数，从而影响渗流场[6]。

流体在孔隙中的流动符合Darcy定律，同时满足Biot方程，土体渗流-应力耦合模型的控制方程[7-10]为

式中：SymbolQC@

为梯度算子，SymbolQC@

2=2x2+2y2+2z2;G为剪切模量，G=E2（1+μ）;ρ为岩体密度;λ为拉梅常数，λ=Eμ（1+μ）（1-2μ）;g为重力加速度;k为土体渗透系数;γw为水的容重;u、v、w分别为土体在x、y、z方向上的位移分量;εv为体应变;βw为水的体积压缩系数;n为多孔介质的孔隙度。

将上述方程组在空间域和时间域离散，其有限元增量表达式为

K-L-LTTΔuiΔpi=-ΔFiΔti{Qi}+ΔtiT{pi-1}（3）

式中：K为通常的刚度矩阵;T为渗流矩阵;L为耦合矩阵;Δui为位移增量;Δpi为孔隙压力增量;ΔFi为节点力增量;Qi为节点汇源项。

控制方程采用显式迭代运算。先采用有限差分法计算渗流场，再把求得的孔隙压力增量加载到应力场，再采用有限元法求解应力場，根据应力场计算得到应变修正渗透率和孔隙率，再反馈给渗流场，循环迭代，直到结束。

3 有限元模型及主要参数取值

根据防洪墙设计方案和地质资料，等比例建立三维有限元模型[11]，如图2所示，共13万个单元，7.4万个节点。水平向外江侧即右侧为x轴正向，堤防轴线水平向纸面为y轴的正向，竖直向上为z轴的正向，反之为负。

挡水变形计算时应充分考虑初始地应力，施工中的开挖、打桩和回填会引起地应力的释放和重分布。经试算发现，对防洪堤的开挖、打桩和回填等施工过程进行逐步演算可较好地实现系统的应力初始化。计算时，根据水位进行渗流场与应力场的耦合[12]，孔隙水压力、承台扬压力、防渗墙前后的水压力和渗透压力均由渗流分析确定[13]。

防洪墙挡洪压力按静水压力计算，土层、桩和墙身界面的接触采用了面-面接触[14]。接触采用罚函数法，界面双向检测，接触刚度采用混凝土的弹性模量控制，综合摩擦系数取0.4。

模型包含钢筋混凝土及各岩土层。墙身及桩基采用C20钢筋混凝土（钢筋体积占比为1%），钢筋混凝土本构采用整体式的弹性模型，σ=Eε，这里E为弹性模量，ε为应变，主要物理参数见表1。各土层采用摩尔库仑模型[15]，其屈服函数为

τn=C-σntan φ（4）

式中：τn为剪应力;σn为正应力;C为类材料的黏聚力;φ为材料的内摩擦角。

各土层主要物理参数见表2。

4 参数和模型的率定

4.1 敏感性分析

为检验计算成果对参数的敏感性，提高模型率定的效率，先分析防洪墙位移对主要地质参数的敏感性。

杂填土位于顶层，覆盖厚度8～10 m，是影响防洪墙位移的最主要因素，对该土层的主要力学参数进行敏感性分析。由于水位不同，地基塑性区的大小存在较大差异，可能会引起敏感性的差异，因此分别对外江低水位23.38 m和高水位27.34 m两种情况进行敏感性分析，敏感性参数为杂填土变形模量E100-200、黏聚力C和内摩擦角φ，变化率分别单独取100%、75%、45%、30%、15%、0%、-15%、-30%和-45%，位移变化率与参数变化率的关系如图3所示。

经计算，对高、低水位两种情况，防洪墙的位移与E100-200、φ和C值负相关;外江低水位23.38 m时，防洪墙位移对杂填土的E100-200最敏感，对φ次之，对C最不敏感;外江高水位27.34 m时，参数改变量在-50%～0%时，位移对3个参数的敏感性十分接近，改变量在0%～50%时，位移对φ值最敏感，对C次之，对E100-200最不敏感。

外江在高、低水位情况下，防洪墙位移对各参数的敏感度不一样;低水位时，防洪墙变位较小，防洪墙位移对E100-200最敏感;高水位时，防洪墙变位较大，防洪墙位移对φ最敏感，地基发生了塑性变形，且挡水越高，塑性区越大，对杂填土的E100-200越不敏感，表明塑性区扩大的过程，也是位移由E100-200主导过渡到由抗剪强度主导的过程。

4.2 参数和模型的率定

地质资料给出了地质参数建议值，为了提高计算精度和可靠度，采用堤防位移观测值对地质参数和计算模型进行反演和率定。

2005年洪峰水位达到27.34 m而发生漫顶，但受当时条件限制，未能获取有效的观测数据，堤防大变位产生了较大塑性区，未能完全复位，此后2006年和2008年的洪峰水位虽高于堤顶地面，但均远低于2005年的洪峰水位，这两次所测防洪墙位移数据均不能反映地基原本的力学特性。2004年洪峰水位为23.38 m，对应防洪墙位移观测值为1.73 cm，可用于反演。

以地质建议参数为初值，根据2004年观测值和参数敏感性分析成果，对地质参数和模型进行大量反演试算，确定杂填土E100-200为9 MPa，φ为10°，C为4.9 kPa。φ比地质报告建议值大2°，C比地质报告建议值大

2.9 kPa，表明建议值偏安全，保留了一定的富余。洪峰水位为23.38 m时，防洪墙水平变位分布如图4所示。

经率定的地基参数和模型具有较高的可信度，可在后续的研究中采用。

5 超标洪水作用下的大变位分析

发生超标洪水后，堤后的人行道、路缘石发生了破坏，这表明堤防在挡洪时发生了较大变位，但堤防的安全性和桩基及桩周土体情况仍难以判断，例如大变位时，桩基是否发生破坏、断裂，桩基破坏的程度和形式，鉴于此，有必要通过对漫顶工况的复核和论证，评估洪水漫顶后堤防的破坏程度和安全性，定性分析维修加固和重建的必要性，同时通过对大变位机理和桩基受力特性的定量分析，为后续维修或加固方案的提出提供依据。

漫顶时外江洪峰水位为27.34 m，堤内水位为21.50 m。经计算，地基总水头分布如图5所示，等值线密集于挡水墙、承台和防渗墙。防洪墙水平变位如图6所示，最大水平位移为5.06 cm，位于堤顶;堤内地面处的堤身水平位移为3.70 cm，承台水平位移为2.30 cm;承台和墙身发生水平位移的同时，墙身悬肩结构也发生了微小的逆时针偏转，并同时带动承台附近的地基土也向堤后变位，越靠近承台，变位越大。

桩和承台应力水平力较小，如图7所示。各桩受压，经单元应力积分，求得左一排桩（x轴负向侧第一排，下同）和右一排桩（x轴正向侧第一排，下同）桩顶内力，见表3，中间桩的值介于这两排桩之间。对桩顶竖向力拉为正，水平力向左为正，弯矩垂直纸面向外为正，反之则相反。

经复核，桩身内力在桩身强度设计范围内，满足结构安全要求，主体结构仍未发生破坏，但要满足工程和堤后设施的使用要求，仍须对堤防进行维修加固。

墙后地面附近、承台和齿墙后附近区域土体存在大应变区，如图8所示。对大应变区进行补强加固是堤防变位控制最直接、最有效的途径。

6 除险加固分析

为了减少防洪堤的变位量，并减少塑性区，需要对地基进行加固;为了增大地基水平刚度，需要对主要压应变区进行加固;主要拉应变区也需要进行加固，以防止发生水力劈裂。

堤后为公路，路旁有密集民居，作业空间有限。根据工程地质条件和主要应变区的分布，拟对主要大应变区采取充填灌浆的方法进行加固，加固范围如图9所示。根据抽样试验，充填后的土体渗透系数取5×10-5cm/s，饱和容重取21 kN/m3，E100-200取20 MPa，C取15 kPa，φ取20°，其他土层参数取值与原土相同，分别验算设计洪水位为26.47 m时防洪墙在加固前后的状态。

经计算，充填灌浆加固后，堤基渗透性降低，地基渗流场重分布，承台的扬压力增加，地基总水力梯度最大值仍在防渗墙顶，但由加固前的6.37降到了加固后的4.78。

与加固前相比，被加固土体的弹性模量和强度增大，应变减小，桩与桩周土体的相对位移减小，防洪堤的变位减小，设计洪水情况下，防洪墙在加固前后的水平位移见表4。与加固前相比，墻顶水平位移减小了43.15%，堤内地平面的墙身水平位移减小了41.28%，承台水平位移减小了39.36%，位移量减小显著，表明充填灌浆效果显著。充填灌浆后防洪墙水平位移分布如图10所示。

充填灌浆前，堤内堤基的主要应变区分布在墙后地面处和承台后侧区;充填灌浆后，被加固的土体的应变减小了，主要应变区分布在墙后地面处和被加固土体后侧区，表明加固体一定程度上传递了堤防的位移，加固前后的地基应变如图11所示。

基础的渗透流场和刚度发生变化，引起桩基结构内力变化，加固前后桩顶内力对比见表5。

加固后，渗透性减小，扬压力增大，承台竖向力减小，左、右排桩竖向压力分别减小20%和4%;左排桩桩顶受承台的水平力向左，减小了7%，右排桩桩顶受承台的水平力向右，增加了116%;左排桩的弯矩减少了11%，右排桩的弯矩方向相反，增加了56%。

左、右排水平力和弯矩方向相反，这似乎与常规经验矛盾。经深入分析，堤防在完建时，外江水位低，桩基挡土，堤防和桩基整体向右变位，右排桩桩顶受承台向右的较大水平力，左排桩在填土压力下，桩顶受承台向左的水平力;挡洪后，地基与挡墙整体向左变位，右排桩桩顶受到承台向右的水平力得到了释放而减小，而左排桩桩顶受到承台向左的水平力得到了加强而增大。各桩的受力状态存在差异，与堤防后方的高填土有关，体现了该工程结构受力的复杂性和特殊性，若仅按常规经验设计或简单套用规范，将产生较大误差，甚至错误。

充填灌浆后，承台水平位移刚度增大，桩基和墙体总体分载的水平抗力减小，扶壁挡墙的应力也有变化，但变幅微小。扶壁挡墙和桩基的应力分布如图12和图13所示。复核控制断面的配筋，结构和桩基强度均能满足规范要求，表明该方案有效且安全可行。

7 结论与建议

建立三维流固耦合数学模型，在对地基参数进行敏感性分析和参数反演的基础上，分析了防洪墙在超标洪水下的响应和加固的必要性，然后提出充填灌浆加固，并验证其有效性和可靠性，主要结论如下。

（1）堤防小变位时，变位由变形模量主导;大变位时，变位由抗剪强度主导。

（2）地基参数建议值存在一定的富余。

（3）防洪堤在洪水漫顶时，堤防主体结构仍未破坏。结合堤后设施的使用要求，通过维修加固可满足工程的使用要求。受高填土及地基变形的相互影响，桩基的各排桩受力存在较大差异。

（4）齿槽后方地基采用充填灌浆加固后，可有效减小防洪堤变位量，也满足结构强度规范要求。

本文仅对一种加固方案进行了分析，下阶段可利用类似方法对地基加固范围、加固体强度和各桩受力的差异等进行进一步研究，通过经济、技术比较对方案进行选优。工程实施后，还可根据观测数据对堤防加固后的变位特性进行进一步研究，为类似工程的设计和除险加固提供参考。

参考文献：

[1] 宋力，宋万增，高玉琴，等.引黄涵闸引水涵洞地基竖向应力分布规律[J].人民黄河，2015，37（1）：126-129.

[2] 蔡超英，藏光文，徐兵.高填土空箱扶壁式翼墙铅直墙背受力测试研究[J].人民黄河，2006，28（3）：67-68.

[3] 黄波，张亮.东平湖石洼分洪闸抗滑稳定加固设计[J].人民黄河，2013，35（12）：106-108.