高压油管的压力控制

郭士康 沈家辉

摘要：高压油管是高压油路的组成部分，油管要能承受一定的油压而有一定的疲劳强度，保证管路的密封要求。车用高压油管主要出现在高压喷射的柴油机和高压喷射的直喷汽油机中，能承受发动机运转过程中所需的油壓。本论述主要结合2019年全国大学生数学建模竞赛A题，在高压燃油系统中，将燃油视作均质流体运用流体力学、阿伏伽德罗定律和伯努利方程，建立数学模型，研究单向阀、高压油泵以及凸轮等部件对燃油进入和喷出的间歇性T作过程、高压油管内压力变化、发动机的工作效率等方面的影响。

关键词：阿伏伽德罗定律;伯努利方程;流体力学;数学模型

中图分类号：TK421+.4

文献标志码：A

1概述

高压油管是高压油路中的重要组成部分，随着我国机械工业的快速发展，高压油管被应用于各个行业之中，其工作效率和优越的性能得到了极大的认可[1]。其用途十分广泛，如用于汽车、柴油机、挖掘机等。这决定了高压油管品种的多样性和复杂性，进而要求高压油管具备高质量和高性能。研究高压油管对提高发动机效率、推进机械工业及其他产业的发展具有重大意义。

2模型建立与求解

2.1问题一模型的建立与求解

问题（1）：高压油泵在入口处提供的压力恒为160MPa，高压油管内的初始压力为100MPa。如果要将高压油管内的压力尽可能稳定在100MPa左右，如何设置单向阀每次开启的时长？如果要将高压油管内的压力从100MPa增加到150MPa，且分别经过约2s、Ss和10s的调整过程后稳定在150MPa，单向阀开启的时长应如何调整？

问题（2）：在实际工作过程中，高压油管的燃油来自高压油泵的柱塞腔出口，喷油由喷油嘴的针阀控制。凸轮驱动柱塞上下运动，柱塞向上运动时压缩柱塞腔内的燃油，当柱塞腔内的压力大于高压油管内的压力时，柱塞腔与高压油管连接的单向阀开启，燃油进入高压油管内。针阀升程为0时，针阀关闭;针阀升程大于0时，针阀开启，燃油向喷孔流动，通过喷孔喷出。在问题1的基础上，确定凸轮的角速度，使得高压油管内的压力尽量稳定在100MPa左右。

问题（3）：在问题2的基础上，再增加一个喷油嘴，每个喷嘴喷油规律相同，喷油和供油策略应如何调整？为了更有效地控制高压油管的压力，现计划在D处安装一个单向减压阀。单向减压阀打开后高压油管内的燃油可以在压力下回流到外部低压油路巾，从而使得高压油管内燃油的压力减小。请给出高压油泵和减压阀的控制方案。

2.2问题一模型的建立与求解

温度、溶解度与黏性条件如下：

分子间热运动加剧，会导致高压油管的温度上升。温度骤然发生变化时，容易导致油管壁的材料、形状等发生变化，从而使得问题无法求解。故在进油与出油过程中，将高压油管内视为恒高温状态，油管的一系列参数都可近似等效为不变。由于在高温条件下，液体对气体的溶解度大大降低。为简化计算过程，将燃油对管内气体A的溶解度视为0。

自然界中的实际流体都具有粘性，所以实际流体又称粘性流体，是指流体质点间可流层间因相对运动而产生摩擦力而反抗相对运动的性质。对于一定的液体，内摩擦力F与两流体层的速度差△u成正比，与两层之间的垂直距离△v成反比，与两层间的接触面积S成正比，即：

F=u△u/△y·s

（1）

根据阿伏伽德罗定律定律p·v=n·R·T，同温，同物质量的情况下，V越大，P越小。

由题意可得，问题一中的隐藏条件为：针阀以100ms为一个工作周期，1s内工作10次。每个工作周期包含实际工作时间2.4ms和虚拟工作时间97.6ms。根据这个隐藏条件，我们可以得出：在一定时间内，进油量等于出油量时，高压油管内的压力才能近似保持为100MPa[2]。

而为了使管内压强在2s、5s、10s内迅速上升到150MPa，就必须在管内积累一定量的燃油，才能使管内压强上升。并在2s、5s、10s之后，再调整进油口的速率，稳定管内压力为150MPa。

根据题中已知条件，可得高压油管最大容量，A口单位时间内的进油速率由以下方程组可得：

QA=C×A×√2△P/ρ

A=pj×（dA/2）^2

△P=160-100

ρ150MPa=ρ100MPa+ρ×△P/E

（2）

B口在一个周期100ms内的出油量，由图1可知：

得到在100 ms内YB为44mm3。

然而单向阀开关控制供油时间的长短，单向阀每打开一次就需要关闭10ms。为了稳定高压油管内的压力为100MPa，假定在以100ms为一个周期的时间内，进油量与出油量需近似相等，即Y进=Y出=44，设N为在单位时间内，单向阀的关闭次数，则可以得到以下平衡式：

Y进=Y出

（t+10）*N=100

Y进=15.34*t*N

Y出=44

（3）

可求得单向阀供油时间。

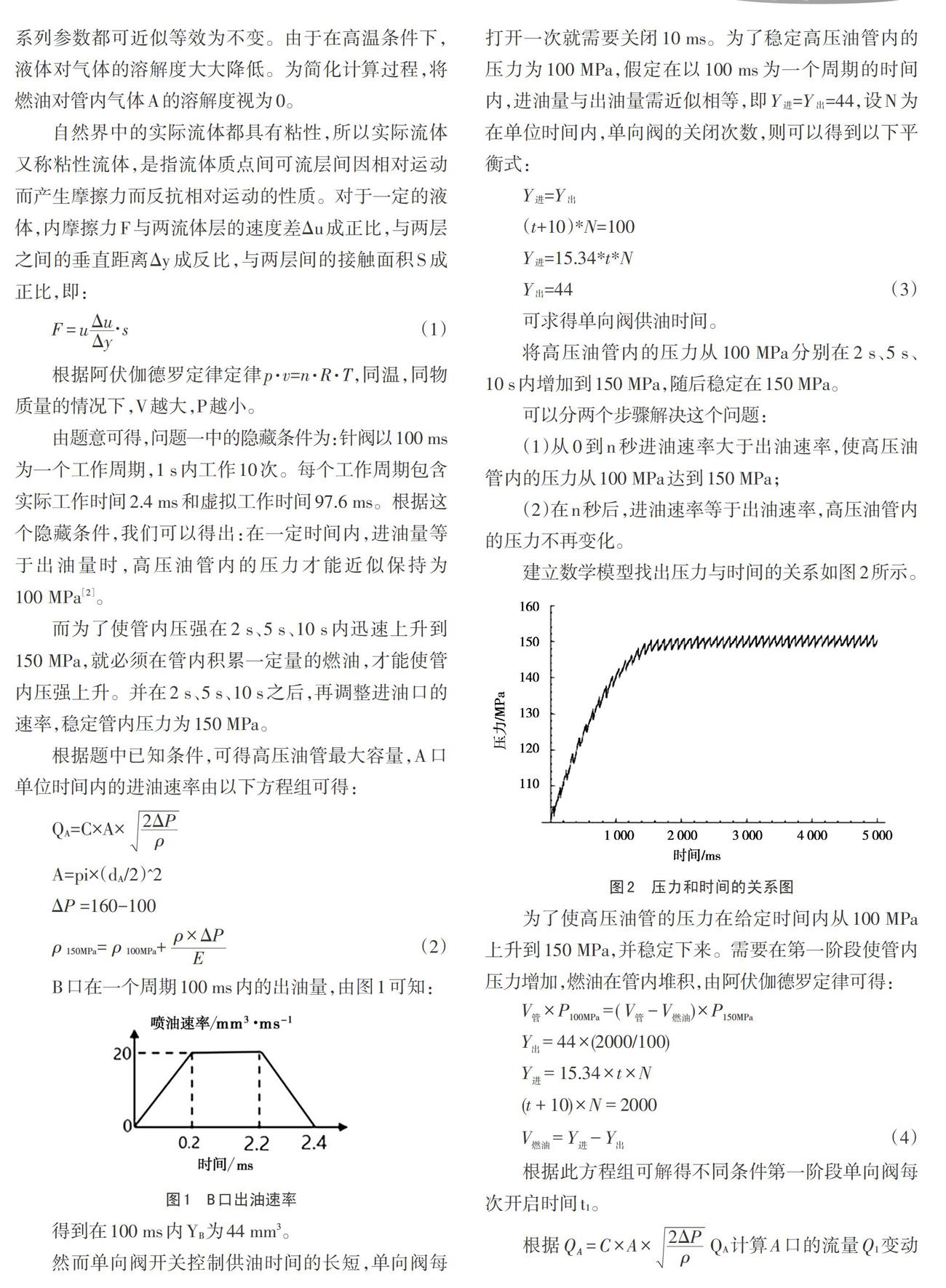
将高压油管内的压力从100 MPa分别在2s、5s、10s内增加到150MPa，随后稳定在150MPa。

可以分两个步骤解决这个问题：

（1）从0到n秒进油速率大于出油速率，使高压油管内的压力从100MPa达到150MPa;

（2）在n秒后，进油速率等于出油速率，高压油管内的压力不再变化。

建立数学模型找出压力与时间的关系如图2所示。

为了使高压油管的压力在给定时间内从100MPa上升到150MPa，并稳定下来。需要在第一阶段使管内压力增加，燃油在管内堆积，由阿伏伽德罗定律可得：

V管×P100MPa=（V管-V燃油）×P150MPa

Y进=44×（2000/100）

Y进=15.34×t×N

（t+10）×N=2000

V燃油=Y进-Y出

（4）

根据此方程组可解得不同条件第一阶段单向阀每次開启时间t1。

根据QA=C×A×√2△P/ρQA计算A口的流量Q1变动之后的值。

第二阶段为了将管内压强稳定在150MPa，在以100ms为一个周期的时间内，需使进油量近似等于出油量，将已知条件代入方程组（3），即可得到不同条件下第二阶段单向阀开启时间t2。

2.3问题二模型的建立与求解

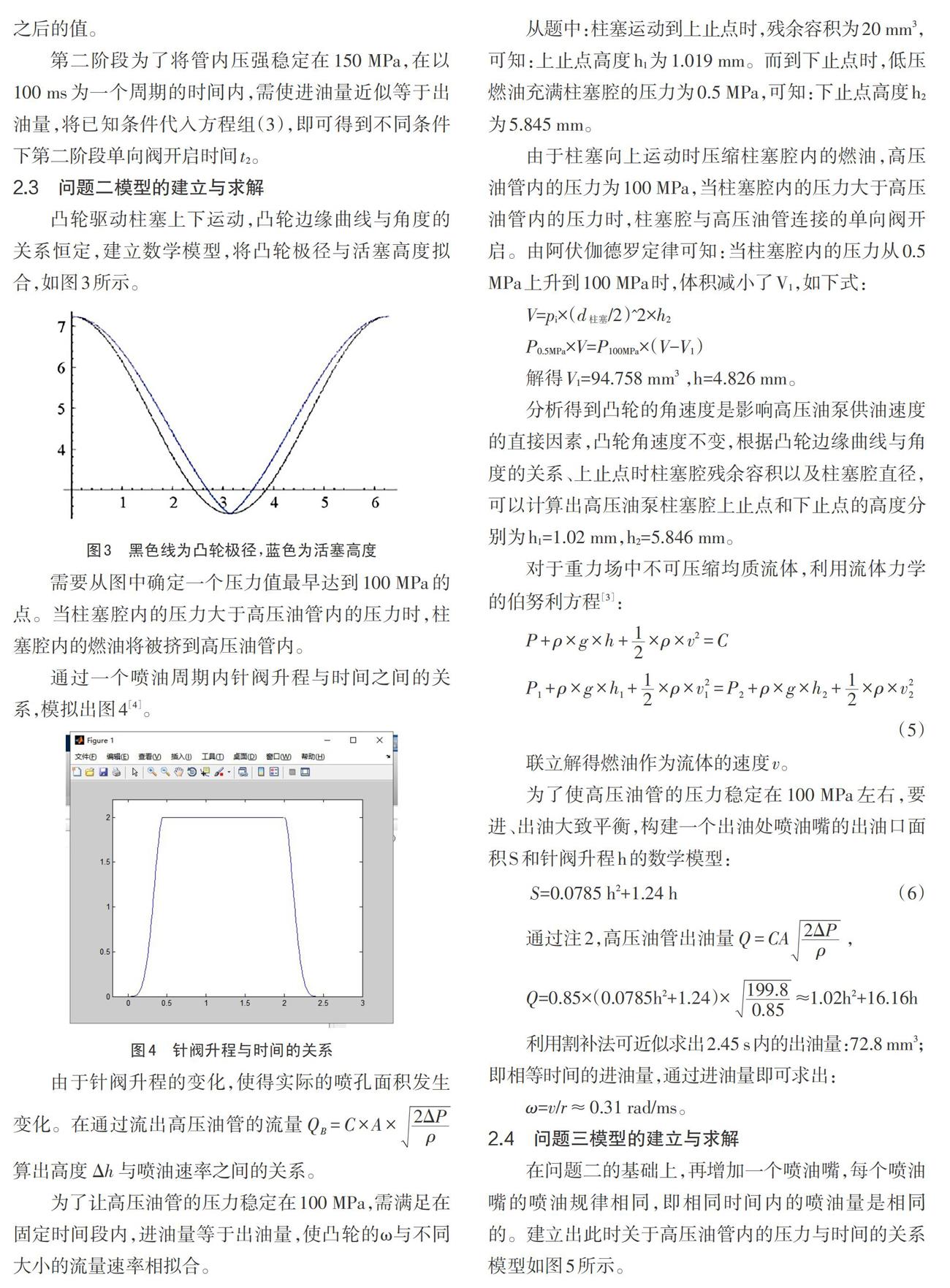
凸轮驱动柱塞上下运动，凸轮边缘曲线与角度的关系恒定，建立数学模型，将凸轮极径与活塞高度拟合，如图3所示。

需要从图中确定一个压力值最早达到100MPa的点。当柱塞腔内的压力大于高压油管内的压力时，柱塞腔内的燃油将被挤到高压油管内。

通过一个喷油周期内针阀升程与时间之间的关系，模拟出图4[4]。

由于针阀升程的变化，使得实际的喷孔面积发生变化。在通过流出高压油管的流量QB=C×A×√2△P/ρ算出高度△h与喷油速率之间的关系。

为了让高压油管的压力稳定在100MPa，需满足在固定时间段内，进油量等于出油量，使凸轮的ω与不同大小的流量速率相拟合。

从题中：柱塞运动到上止点时，残余容积为20mm3，可知：上止点高度h1为1.019mm。而到下止点时，低压燃油充满柱塞腔的压力为0.5MPa，可知：下止点高度h2为5.845mm。

由于柱塞向上运动时压缩柱塞腔内的燃油，高压油管内的压力为100MPa，当柱塞腔内的压力大于高压油管内的压力时，柱塞腔与高压油管连接的单向阀开启。由阿伏伽德罗定律可知：当柱塞腔内的压力从0.5MPa上升到100MPa时，体积减小了V1，如下式：

V=pi×（d柱塞/2）^2xh2

P0.5MPa×V=P100MPa×（V-Vi）

解得V1=94.758mm3，h=4.826mm。

分析得到凸轮的角速度是影响高压油泵供油速度的直接因素，凸轮角速度不变，根据凸轮边缘曲线与角度的关系、上止点时柱塞腔残余容积以及柱塞腔直径，可以计算出高压油泵柱塞腔上止点和下止点的高度分别为h1=1.02mm，h2=5.846mm。

对于重力场中不可压缩均质流体，利用流体力学的伯努利方程[3]：

P+ρ×g×h+1/×ρ×v2=C

P1+ρ×g×h1+1/2×ρ×v2=P2+ρ×g×h2+1/2×ρ×v22

（5）

联立解得燃油作为流体的速度v。

为了使高压油管的压力稳定在100MPa左右，要进、出油大致平衡，构建一个出油处喷油嘴的出油口面积S和针阀升程h的数学模型：

S=0.0785h2+1.24h

（6）

通过注2，高压油管出油量Q=CA√2△P/ρ，

Q=0.85x（0.0785h2+1.24）x√199.8/0.85≈1.02h2+16.16h

利用割补法可近似求出2.45s内的出油量：72.8mm3;即相等时间的进油量，通过进油量即可求出：

ω=v/r≈0.31rad/ms。

2.4问题三模型的建立与求解

在问题二的基础上，再增加一个喷油嘴，每个喷油嘴的喷油规律相同，即相同时间内的喷油量是相同的。建立出此时关于高压油管内的压力与时间的关系模型如图5所示。

在此，通过角速度ω的不同可将进油速率分为三个阶段：

（1）ω≤ω0：根据喷油嘴C距A口比喷油嘴B近，假设从A口的进油量全部由喷油嘴C进行排出，喷油嘴B不工作;

（2）ω1>ω>ω0：此时A口的进油量远大于喷油嘴C所能排出的量，喷油嘴B开始工作。喷油嘴B、C同时工作能够及时排出完来自于A口的进油量;

（3）ω>ω1：这时候，喷油嘴B和C同时工作仍然不能及时排出来自于A口的进油量。每处作一段时间，就会在管内积压一定量的燃油。高压油泵长时间工作会导致管内的积油量逐渐上升，直到燃油充满油管。

在管内安装一个单向减压阀，打开后高压油管内的燃油可以在压力下回流到外部低压油路中，从而使得高压油管内燃油的压力减小。这种方式可以很大程度上减小当ω>ω1，时管内积累燃油的风险。

为了使喷油嘴的使用效率最大化，A口的进油速率应该满足：让喷油嘴B和C都ω作，但最大值不应该超过两个喷油嘴在100ms内的最大排油量。为简化计算，将两个喷油嘴同时工作近似等效为一个喷油嘴工作。高压油管出油量Q0=2×CA√2△P/ρ

Q=2×0.85×（0.0785h2+1.24）×√199.8/0.85≈2.04h2+32.32h

利用割补法可近似求出2.45s内的出油量：145.6mm3;即相等时间的进油量，通过进油量即可求出：

ω1=v/r≈0.62（rad/ms）

即：将进油速率转化为凸轮的角速度ω，应满足：

0.62>ω>0.31（rad/ms）

此后，在D处增加了一个单向减压阀。为保证高压油管长期工作的安全性，对单向减压阀设定了一个参考压力值：

P减压=125MPa

由于进油速率过快，管内积攒燃油后，当管内压力大于125MPa时，单向减压阀开启，管内燃油在压力下回流到外部低压油路中。单向减压阀的出油速率Q低压通过以下模型计算：

Q低压=CA√2△P/ρ

△P/△ρ=E/p

（7）

解得：Q低压≈22.265mm3/ms。

3模型的评价与推广

本论述通过对高压油管中各物理量的处理，找出了许多变量之间的潜在关系。并能与实际紧密联系，结合实际情况对问题进行求解，使得模型具有很好的通用性和推广性。但是查阅文献[5]得知温度对阿伏伽德罗定律是有影响的，而且燃油作为液体，会与高压油管壁产生摩擦力，为了模型的简便，本论述未考虑温度和摩擦力的影响。本数学模型建模方便，计算简单，便于理解，可操作性强，准确性高，不仅能解决题目中的问题，还可以推广到现实生活中去，用于各种管道的设计与控制问题。

参考文献：

[1]解方喜.柴油机燃油射流运动行为特点及对燃烧的影响研究[D].长春：吉林大学，2010.

[2]李玉婷.柴油机高压油管密封性能分析[D].北京：北京理工大学，2015.

[3]严导淦.流体力学中的总流伯努利方程[J].物理与工程，2014，24（4）：47-53.

[4]蔡梨萍.基于MATLAB的柴油机高压喷油过程的模拟计算[D].武汉：华中科技大学，2005.

[5]张艳燕，刘娟，马晓栋.理想气体状态方程推导中的几个问题[J].新疆师范大学学报（自然科学版），2010，29（4）：70-71.

收稿日期：2020-05-25

作者简介：郭士康（1999-），男，汉族，河南商丘人，大学本科在读，主要研究方向：应用数学。