数学课堂解题教学的策略反思

摘 要：课堂教学应注重对典例的分析，重视通性通法，渗透数学思想方法，丰富学生的命题等价系统，并作针对性的适当拓展，拓展学生的数学视野，进而提高其解题能力。

关键词：数学解题;通性通法;思想方法;教学策略

学数学离不开解题，重视数学解题，又不能落入题海，这需要科学进行解题训练，也对教师自身的研题能力和解题教学能力提出更高的要求。将解题经验算法化，显性化，建立系统的解题模块，丰富数学命题的联想系统，能有效地帮助学生找到解题的思路。历年的高考试题资源丰富，同时经过各地模拟试题变式演化，得到了充分地拓展。面对如此众多的题目，教师如何选择取舍，如何以点概面，如何渗透思想方法和丰富学生们的解题经验和系统，激发他们解决数学问题的潜力和热情，对高中教学的主要阵地——课堂的教学就提出了更高的要求。基于此，笔者从以下四个方面对数学课堂解题教学进行反思总结。

一、 注重通性通法以提高解题效率

高考数学试题注重基础知识和基本方法的考查，有些试题时常可以从教材的例题或者习题中找到熟悉的背景，体现了“注重通性通法，淡化解题技巧”，这种模式化的解题思路，是由已知条件出发，逐步分析，自然总结得到，贴近学生的思维认知层次，符合思维习惯，较容易引起共鸣。典型试题承载着丰富的思想和方法，能够揭示一般的规律，植根基础，内涵广泛，是各级考试命题的源泉，可以帮助学生巩固数学基础知识和熟练解题的基本方法。因此，在教学中，教师应整体把握知识脉络，充分重视学生的知识基础，在典例教学中引导和启发通法应用，使学生形成常规的解题意识和能力，从而能独立思考和解决基础问题，帮助学生达到数学思维的自然化，这种教学策略对学生数学学习的承接至关重要。

解题大师罗增儒认为，分析典型例题的过程是学会解题的有效途径，所以在模式化解题的教学过程中，应该重视对教材典例的分析，让学生养成严密的逻辑思考习惯，同时也注意避免因题境熟悉而陷入定势思维。

二、 渗透思想方法以加深数学理解

对于数学概念或数学命题的学习，学生往往只重视记忆与应用，而忽略在概念生成过程或命题的证明过程的学习，而其中往往渗透着常用的数学思想方法（函数与方程思想，数形结合思想，化归与转化思想，分类讨论等思想），教学中能让学生体会和理解，可帮助学生做好知识的梳理，更自然的在解题中得到应用。数学思想方法的渗透能帮助学生在后续解题学习中学会对题目的提炼和升华，对各种方法的类比和转化，是数学解题过程中的重点和难点。

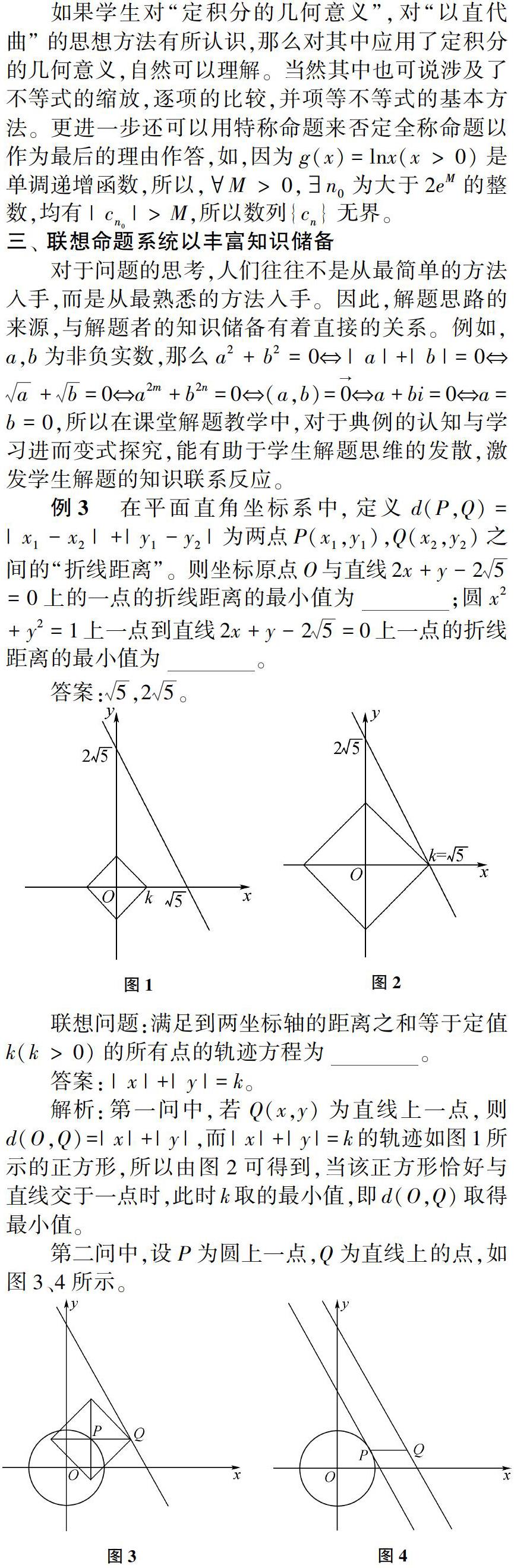
由图3就确定了相对于圆上任一点P，使得d（P，Q）最小的Q的位置所在，而通过图4就进一步确定了P的位置，即将直线平移至相切位置，从而本题迎刃而解。

四、 适当延伸拓展以激发学习潜力

高考数学重视通性通法，而不会一味追求解题的技巧。但是针对试题中的难题，对考生独立分析问题和解决问题的能力，对数学的逻辑推理和数学运算、数据分析等核心素养能力，甚至对考生的意志品质方面都提出了更高的要求。尤其信息题、创新题一类，经常涉及高等数学的一些概念，而又能与中学数学知识与方法相互联系或类比的题型，所以平时教学中，有针对性的引入拓展，能帮助学生在面对陌生题境之时，更加从容淡定，也能为学生将来进一步学习数学，打下良好的基础。例如在函数模型的教学中适当介绍函数的凹凸性;在常用逻辑用语中，灵活应用数学符号“，”进行数学概念或命题的表达（如最值，上下界，上下确界等）;在圆锥曲线学习中众多的经典问题和某些必要的二级结论的推导;在导数学习中，理解二阶导数与原函数的凹凸性关系，了解中值定理或泰勒展开等知识，都能让解题者以更高的视角来看待问题。在各地的试题中，这样的问题屡屡出现（就如例2中的调和级数的发散），这里不再举例赘述。当然，这部分内容的拓展应该行之有度，视具体学情而定，避免让学生感觉吃力、望而生畏，反而降低其对数学的兴趣;同时也对教师的数学素养提出更高的要求。

課堂教学中，解题的教学往往需要师生共同进行有效地思考和探究性的对话，往往充满着质疑与思辨，能够激发学生的学习潜力，使学生有效的综合运用所学知识的同时，提高理性思维能力，培养学生的数学思维的宽度和广度，发展其数学核心素养。

波利亚曾经指出：掌握数学就意味着善于解题。同时，解题能力对于培养学生学习数学的兴趣及能力有着至关重要的作用，因此，教学中，教师应积极探究教学策略，寻找可以帮助提高学生解题能力的教学方法，通过师生之间默契的配合，让学生面对数学问题时，得到解法的自然流露，从而激发其主动思考问题和分析解决问题的潜力，有效提高其学习数学的兴趣。

参考文献：

[1]陈永明数学工作室.数学习题教学研究[M].上海：上海教育出版社，2010.

作者简介：林海川，福建省漳州市，福建省漳州市东山第一中学。