基于灰狼算法的近红外光谱变量选择方法研究

武新燕，卞希慧,*，杨 盛，徐 沛，王海涛

(1.天津工业大学 省部共建分离膜与膜过程国家重点实验室，环境科学与工程学院，天津 300387；2.天津工业 大学 化学与化工学院，天津 300387；3.绍兴市柯桥区污染物总量控制中心，浙江 绍兴 312030)

近红外光谱因其快速、方便、低成本以及无损等优势，已广泛应用于诸多领域[1-7]。然而，近红外光谱同时存在变量维度高，多重共线性，包含冗余信息和高频噪声等问题，直接构建预测模型不但增加建模复杂度，同时也会影响模型的预测性能和泛化能力[8]。因此选择信息最丰富的变量或剔除信息不丰富的变量变得尤为重要。随着人工智能和计算机技术的迅速发展及应用，变量选择的方法研究也取得了较大的进展。主要有基于统计学的变量选择方法[9-11]，基于单一指标的波长选择方法[12-13]和群体智能优化算法[14-18]。其中群体智能优化算法因其强大的全局搜索能力，使得其在特征变量筛选方面具有巨大的潜力。

灰狼优化(Gray wolf optimizer，GWO)算法是由Mirjalili等[19]于2014年开发的一种群体智能优化算法。GWO模拟灰狼群体捕食行为的特性，其主要设计思想是基于狼群按个体的能力划分社会等级，选出狼群的领导者，通过狼群追踪、包围、追捕、狩猎猎物等过程达到优化搜索的目的，狩猎过程即算法寻优过程。与其它群体智能优化算法相比，GWO算法因参数少，结构简单，易于实现，在求解优化问题上具有很好的局部搜索能力和求解精度，受到研究者的广泛关注[20]，并广泛应用于多种领域的理论研究和实际生产中[21-23]。由于GWO算法目前在光谱分析领域应用较少，本文探讨了GWO算法在近红外领域应用的可行性。选用玉米样品的近红外光谱，考察了优化过程中狼群性能的变化，迭代次数及狼群数量对模型性能的影响，将参数优化后的GWO算法用于玉米中蛋白质、脂肪、水分及淀粉组分的变量选择，并建立偏最小二乘(PLS)模型。结果表明，与全光谱的PLS模型相比，GWO-PLS算法不仅采用的变量少，而且可以明显提高模型的预测精度。

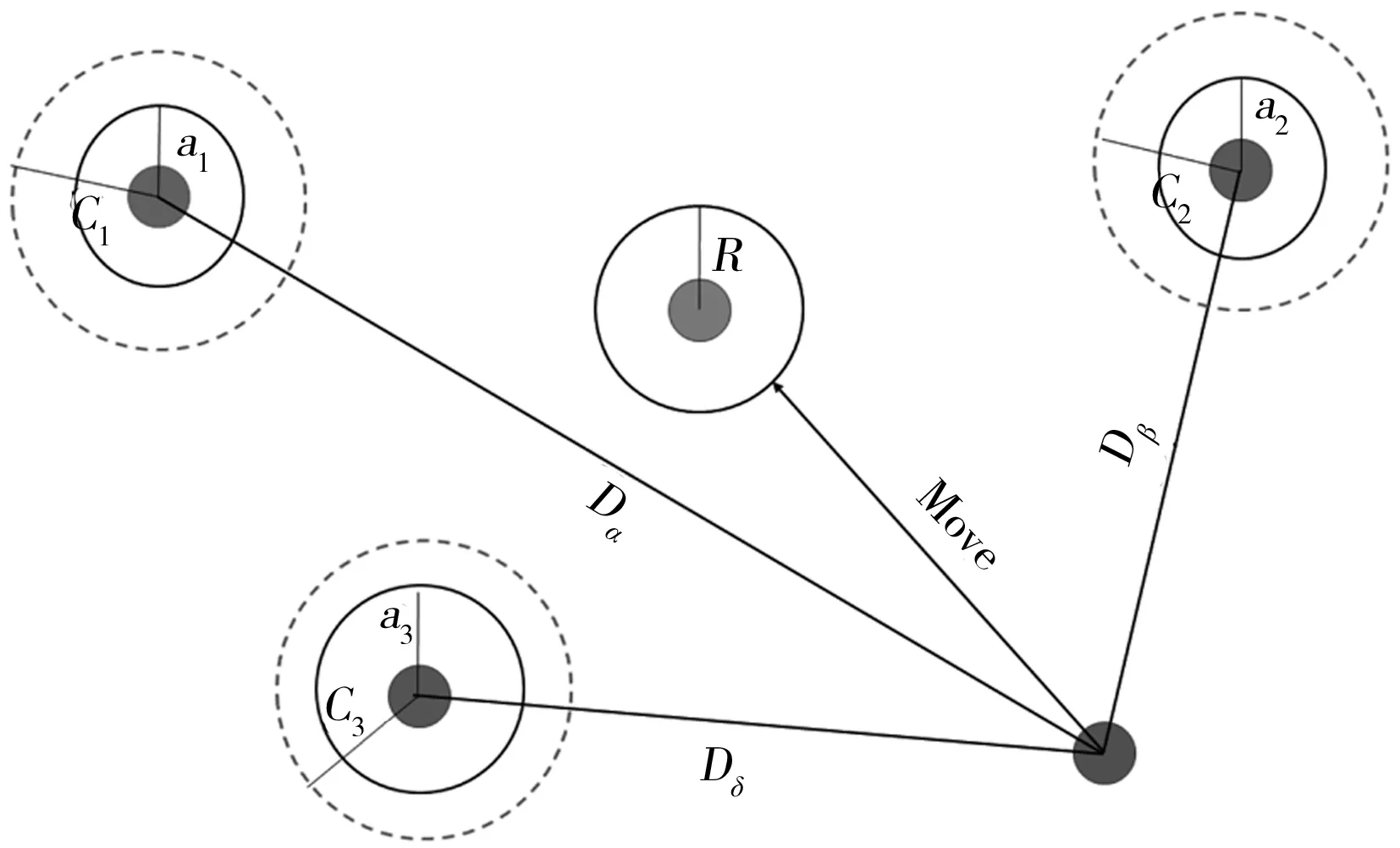
图1 灰狼算法原理图Fig.1 Schematic diagram for GWO algorithm

1 实验部分

1.1 灰狼算法

GWO算法灵感来自于犬科的灰狼。灰狼群居，在捕猎过程中它们分工明确、共同合作进行捕猎。领导能力最强的灰狼被记为α，主要负责捕猎过程中的决策部分及管理狼群。剩下的灰狼个体按社会等级被依次记为β、δ和ω。其中β狼和δ狼是等级依次排在后面的两个个体，捕猎中它们会协助α狼对灰狼群进行管理及辅助参与捕猎过程中的决策问题。剩余的狼群被定义为ω，其主要职责是平衡灰狼种群的内部关系及协助α、β、δ对猎物进行攻击。在整个捕猎过程中，首先由α狼带领狼群搜寻、追踪猎物，当距离猎物足够近时，α指挥β、δ狼对猎物进行围攻，并召唤周围的ω狼对猎物进行攻击，当猎物移动时，狼群包围圈也随之移动，直到捕获猎物。GWO算法的原理图如图1所示。图中Dα、Dβ、Dδ表示猎物到α、β、δ狼的距离，C1、C2、C3表示狼的位置对猎物影响的随机权重，a1、a2、a3表示收敛因子。

算法通过包围、追捕、攻击三个阶段进行捕猎，最终捕获猎物即获得全局最优解。具体算法描述如下：

第1步：狼群寻找猎物，当发现猎物可能出现的位置时，狼群会慢慢地包围猎物。

第2步：对猎物进行包围后，β、δ狼在α狼的带领下对猎物进行追捕，在追捕过程中狼群个体的位置会随猎物的逃跑改变，而后可以根据α、β、δ的更新位置重新确定猎物的位置。

第3步：向猎物攻击。攻击是捕猎过程的最后阶段，狼群对猎物进行攻击并捕获猎物，即得到最优解。

本文将GWO算法运用于近红外光谱数据，并以0和1分别代表是否选取该波长点，将与波长点相等的1、0组成的向量作为灰狼算法的输入，交叉验证均方根误差(RMSECV)作为灰狼算法参数优化的衡量标准获取最优参数。

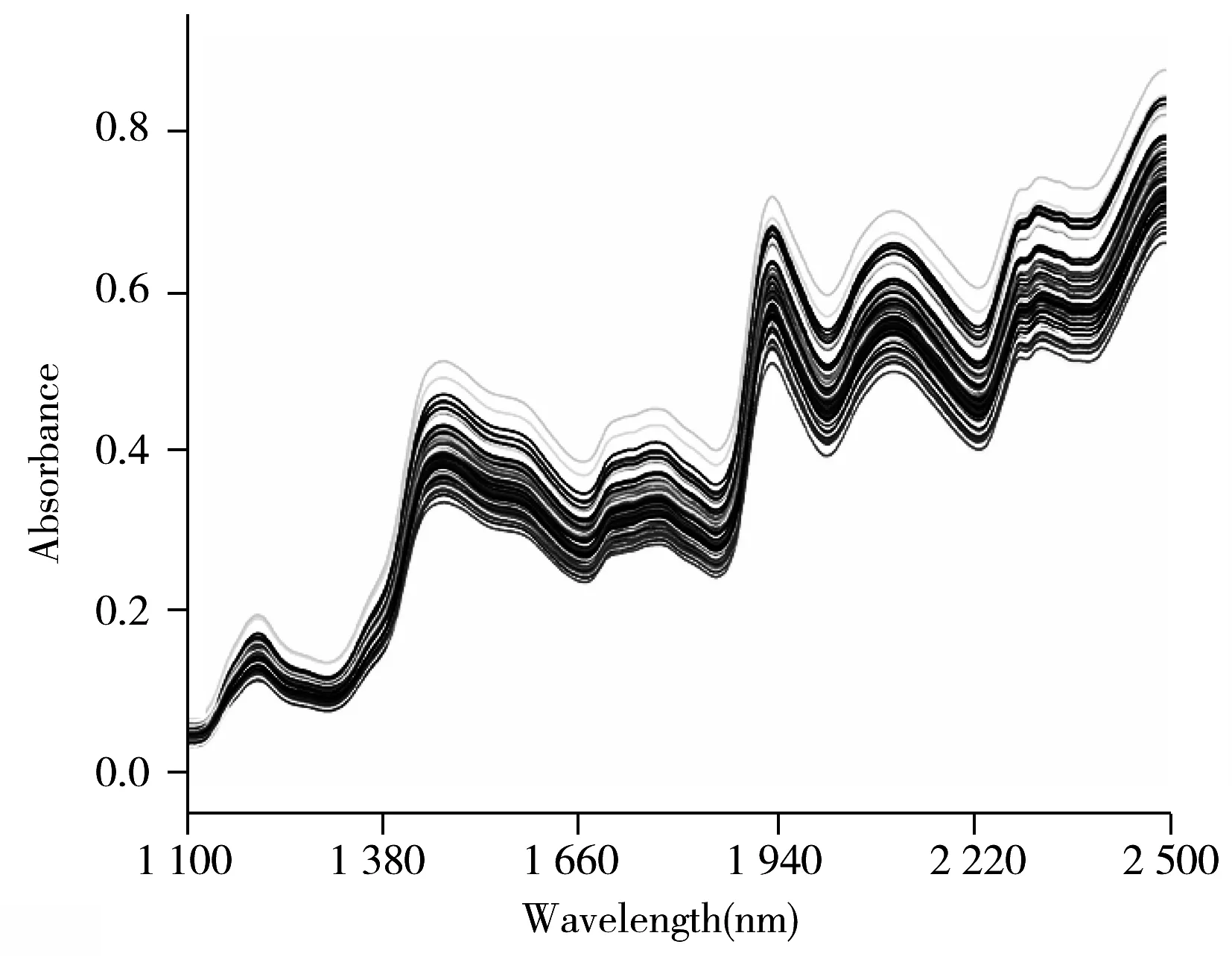
图2 M5仪器采集的玉米样品的近红外光谱图Fig.2 Near infrared spectra of corn samples collected by M5 instrument

1.2 实验数据

为验证GWO算法的有效性，本文对网上公开的玉米数据进行分析。该数据集下载网址为http://software.eigenvector.com/Data/Corn/index.html，由3种光谱仪(M5、MP5、MP6)测定近红外光谱和相应的蛋白质、脂肪、水分及淀粉的含量组成。本文采用M5仪器的光谱，对4种组分进行考察，其中灰狼算法参数讨论以蛋白质组分为主。光谱的波长范围为1 100～2 498 nm，采样间隔为2 nm，共700个波长点(如图2所示)。将80个样品按照Kennard-Stone方法进行分组，选取53个样品用于建立模型，27个样品用于验证模型的性能。

2 结果与讨论

2.1 狼群性能随迭代次数的变化

为了考察狼群性能随迭代次数的变化情况，选取狼群数量为20，迭代次数分别为10、30、60、100、300来表示狼群的寻优趋势，并以RMSECV为预测指标将20匹狼的预测性能显示在图3。从图中可以看出迭代次数为10时(图3a)，20匹狼整体的RMSECV相近;当迭代次数为30时(图3b)，每匹狼的性能差异较大，且整体的RMSECV相比10次迭代时下降;当迭代次数增至60时(图3c)，每匹狼的性能差异明显变小且RMSECV整体下降明显;当迭代次数增至100时(图3d)，20匹狼的RMSECV虽有下降，但与60次迭代时相比下降幅度不大;而当迭代次数达到300时(图3e)，狼群整体的RMSECV相比迭代次数为100时下降明显，且每匹狼的RMSECV几乎相等。说明最优目标值基本寻找到，20匹狼的位置均接近最优解。每个子图中的箭头对应的狼为α狼，可以看出，α狼的位置随着迭代次数的变化而不断变化，在整个寻优过程中α狼不断地更新以靠近目标位置，直至找到最佳位置。

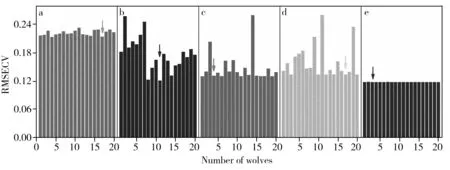
图3 蛋白质组分不同迭代次数中20匹狼的运行结果和α狼的位置Fig.3 The running results of 20 wolves and the position of α wolf in different iterations of the protein a.10 th,b.30 th,c.60 th,d.100 th,e.300 th

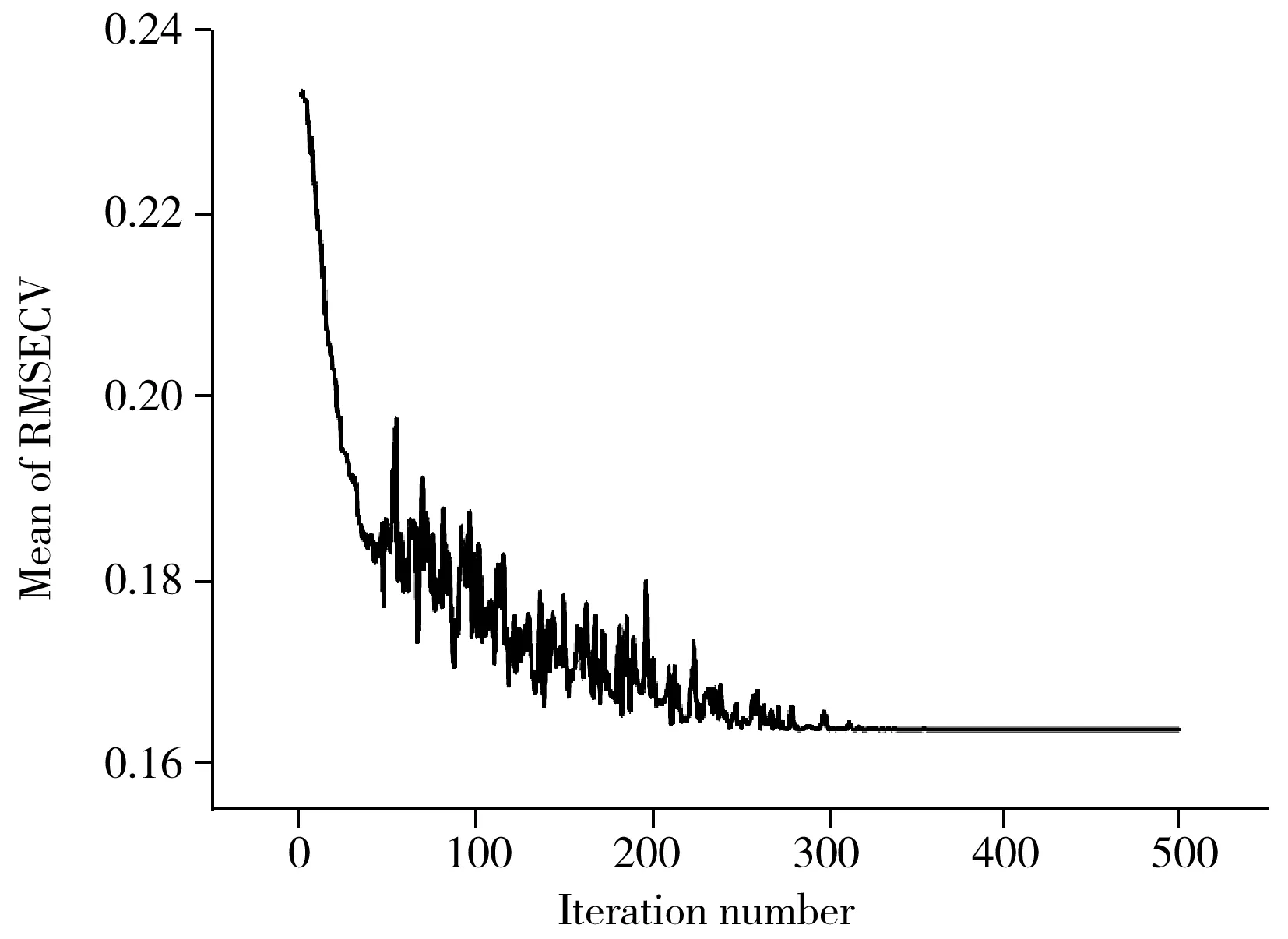
图4 玉米样品蛋白质组分的平均RMSECV随迭代次数的变化Fig.4 Variation of the mean RMSECV with the number of iterations for protein of corn samples

图5 蛋白质组分的RMSECV(a)及运行时间(b) 随狼群数量的变化图Fig.5 Variation plots of RMSECV(a) and runtime(b) with number of wolves for protein

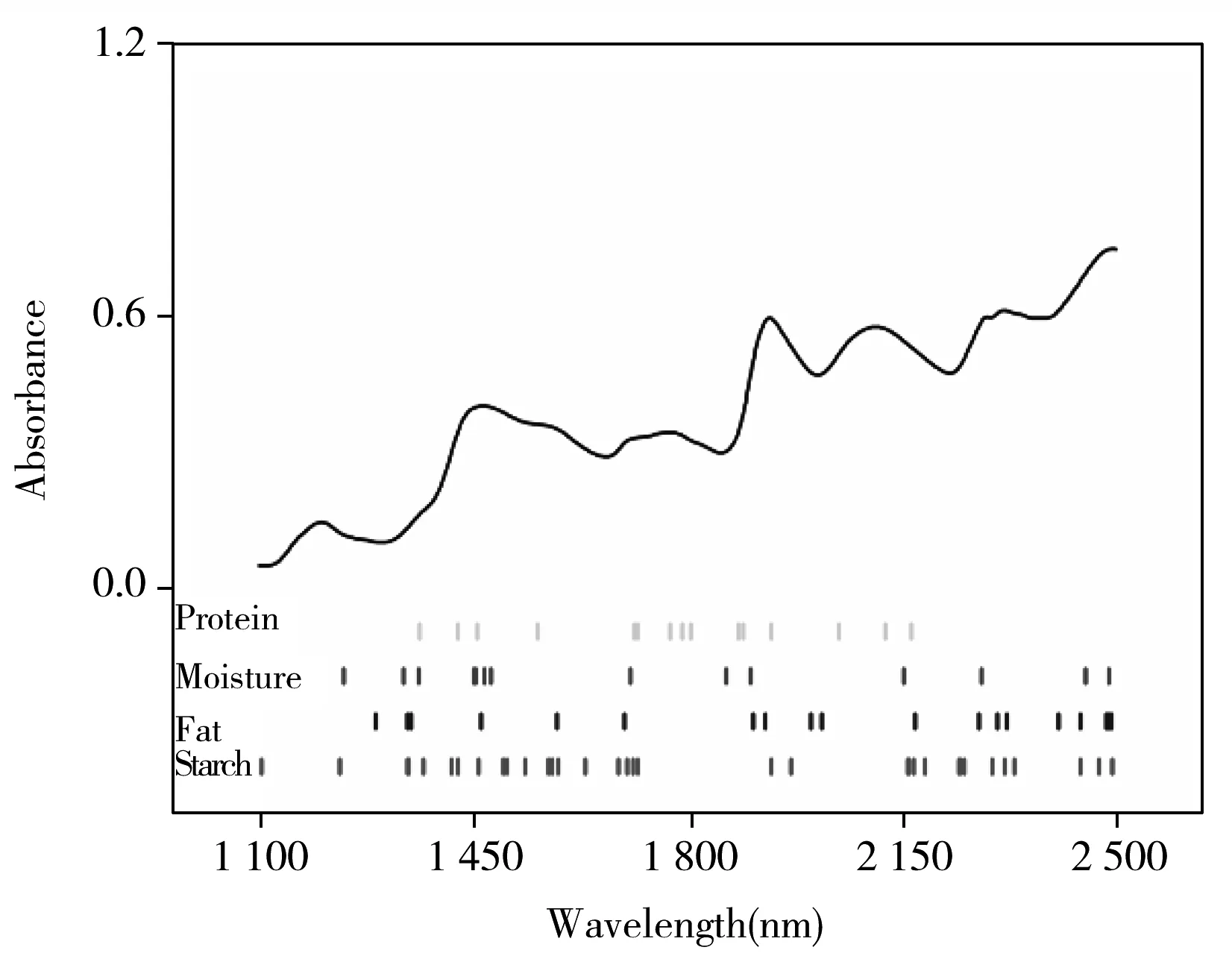
图6 玉米样品波长变量的选择分布Fig.6 Distribution of wavelength variable for corn samples

当灰狼算法的迭代次数达到一定值后，算法整体的结果基本趋于稳定。由于每匹狼的性能有差异，为了进一步考察整体狼群性能，将迭代次数从1变化到500，选取20匹狼的平均RMSECV作为评价标准，得到了玉米样品中蛋白质组分的平均RMSECV随着迭代次数的变化图(如图4)。可以看出，当迭代次数在1～50范围内时，20匹狼的平均RMSECV下降很快。在50～300范围内，20匹狼的平均RMSECV下降趋势较快，并出现较大波动。300次以后，狼群的平均RMSECV不再随着迭代次数变化，说明所有狼匹都聚集在猎物上，即已经寻找到最佳值。因此，迭代次数确定为300。类似可以得到脂肪、水、淀粉的最佳迭代次数分别为350、340、340。

2.2 狼群数量的优化

狼之所以能够战胜体形更大的生物，是因为狼群体协作的结果，因此狼群的数量会影响狼的作战效果。同理，在GWO算法中，狼群数量也会影响GWO算法的性能。为了考察狼群性能与狼群数量的关系，将狼群以间隔为5的数量从5变化到100，以模型预测的RMSECV以及运行时间作为评价模型预测的参数，并得到了RMSECV以及运行时间随着狼群数量的变化图。如图5所示，可以看出RMSECV随灰狼数量的变化波动较大，整体呈下降趋势。当灰狼数量为65时，RMSECV值达到最低，当灰狼数量超过65时，RMSECV值随灰狼数量的增加开始上升。由此可见当灰狼数量为65时可得到满意的结果。同理，可得到玉米样品中其它组分的最佳狼群数量，即脂肪、水、淀粉组分的最佳狼群数分别为100、35、65。另一方面，从运行时间来看，虽然运行时间随着狼群数量的增加基本呈直线上升，但即使灰狼数量高达100时，运行时间也不超过50 s，说明灰狼算法非常高效。因此，在选择狼群数量时，主要参考RMSECV指标，选取65为最佳狼群数量。

2.3 变量选择结果

图6显示了玉米样品不同组分变量选择的分布图，从上到下依次为蛋白质、水、脂肪、淀粉组分。与未经变量选择的波长相比，蛋白质组分经过变量选择后保留的变量数为19，水组分的变量数为14，脂肪组分的变量数为19，淀粉组分的变量数为34。而未经变量选择则有700个变量数。表明使用灰狼算法优化后，每个组分的变量数明显减少。这是由于变量选择将原本存在于全波谱的与建模无关的变量剔除，保留了可用于建立模型的相关变量。经过变量选择后模型的预测精度有所提高，也大大简化了模型计算量，从而验证了算法的可靠性。

2.4 结果比较

采用GWO算法优选波长变量，通过对灰狼算法的参数进行优化可得玉米样品中蛋白质、脂肪、水、淀粉4个组分的最佳迭代次数分别为300、350、340、340，最佳狼群数量分别为65、100、35、65。与直接进行PLS建模的变量数相比，玉米样品的蛋白质、脂肪、水、淀粉这4个组分保留下来的波长数分别为19、19、14、34。将通过GWO算法进行波长选择保留下的变量数建立的PLS校正模型与全光谱建立的PLS校正模型进行比较。模型性能指标主要有预测均方根误差(RMSEP)和相关系数(R)。RMSEP用于衡量预测值与真实值之间的偏差，R则用于反映变量之间相关关系密切程度的统计指标。RMSEP和R值能反映模型的预测能力。RMSEP值越大，R越小，则模型的预测能力越好。计算结果如表1所示。玉米样品的蛋白质、脂肪、水、淀粉组分在进行波长选择前后RMSEP分别从0.245 8、0.122 4、0.339 8、1.105 8下降到0.147 7、0.080 1、0.176 2、0.739 8，RMSEP分别下降了40%、35%、48%、33%。相应的R值在进行波长选择前后分别从0.876 9、0.748 9、0.665 8、0.593 5提高到0.957 0、0.896 1、0.876 9、0.730 7，R值分别提高了8%、16%、24%、19%。数据显示经过波长选择保留的变量数建模后，RMSEP有很大程度的下降，而R值也有一定程度的提升。由此表明经过变量选择后的建模效果更好，模型的预测能力也得到提高。

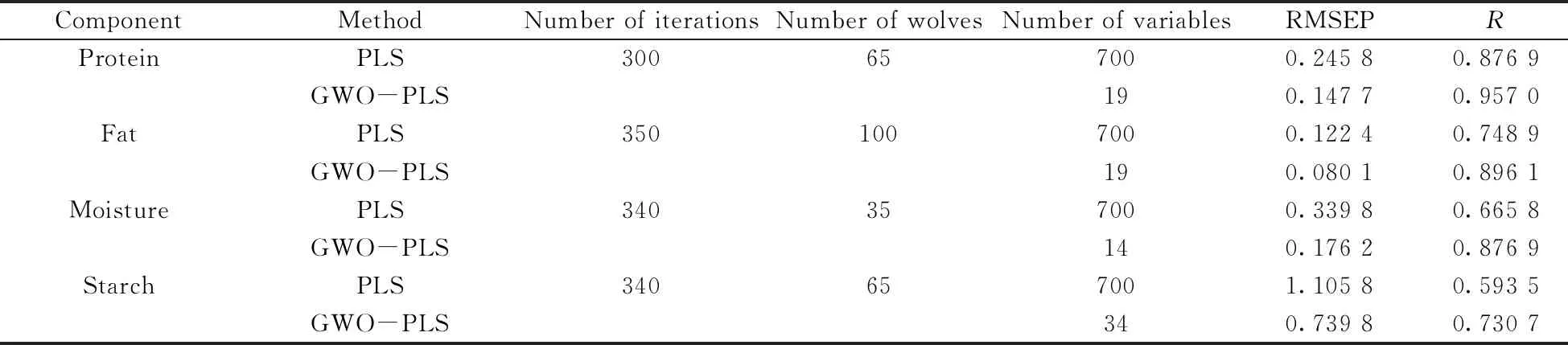
表1 玉米数据不同建模方法结果的比较Table 1 Comparison of the results of different modeling methods for corn dataset

3 结 论

本文提出了基于GWO波长选择的算法结合PLS建立的玉米样品近红外光谱模型，探究了全谱校正模型以及优化组合校正模型对预测结果的影响。该方法以1/0组成的向量表示波长点的选择与否，并作为GWO算法的输入，从而选出需要进行建模的最佳变量数，并同时优化灰狼算法的种群数及迭代次数。在最佳的变量数和优化参数下分别对蛋白质、脂肪、水分和淀粉组分进行定量预测。结果表明，使用GWO波长选择后的少量变量建模比全波长的PLS模型有更低的RMSEP值和更高的R值，运行效率也更高。因此，GWO算法有望广泛应用于近红外光谱的变量选择。