基于DBIRCH算法的Argo剖面数据聚类

邬 满, 张万桢, 孙 苗, 林 森

(1. 广西壮族自治区海洋研究院 信息科, 南宁 530022； 2. 自然资源部 海洋信息技术创新中心, 天津 300171；3. 桂林航天工业学院 实践教学部, 广西 桂林 541004； 4. 桂林电子科技大学 计算机与信息安全学院, 广西 桂林 541004)

0 引 言

我国在2002年初正式对外宣布成为全球Argo计划成员之一, 自2017年12月到2018年11月我国在南海地区投放了132个正常工作的浮标[1], 并已捕获了5 433条温、盐度剖面(此外还包括140条溶解氧、233条叶绿素、233条颗粒物后向散射、156条黄色物质、231条辐射照度以及77条硝酸盐剖面)等海量数据[2]。但因Argo浮标质量把控标准不一致, 使Argo浮标监测数据可信度低, 凸显出如剖面位置异常、毛刺现象、可疑剖面以及盐度漂移等问题[3]。产生大量未经处理原始数据, 故亟需高效快速的数据分析与预处理工具解决Argo浮标监测数据量、数据类型复杂、数据结构不统一且包含大量脏数据等问题, 因此对浮标监测数据有效处理及分析十分必要。

基于聚类分析的数据挖掘算法对改善因Argo浮标常年工作, 受海水、气象和人为等不确定因素的影响导致数据在采集、传输过程中出现的数据偏差, 造成监测数据偏离实际值等问题效果显著[4]。聚类分析作为传统数据挖掘技术, 在数据的分析与提取、数据结构化挖掘及海量数据处理方面应用效果良好, 在社会各领域决策支持活动中扮演着重要的角色。相关专家学者针对海洋数据复杂的数据结构而提出大量基于海洋数据的分析处理方法。但随着全球Argo计划[5]的实行, Argo浮标数量持续性地增长, 数据流量规模越来越庞大, 处理效率要求越来越高。与此同时, 新投放的浮标因地理位置不断变化, 故造成Argo浮标监测数据具有数据量持续增大、时空信息变化频繁、数据结构复杂及时空异构等问题[6], 使传统的数据预处理及聚类分析方法捉襟见肘。因此针对Argo浮标监测数据的聚类分析研究具有极为重要的现实意义。

因此, 为满足海洋Argo浮标剖面观测数据的实时分析需求, 笔者提出一种改进的低复杂度聚类算法DBIRCH(Density-Based Balanced Iterative Reducing and Clustering Using Hierarchies)。改进后的算法降低了对参数的依赖度, 提升了聚类的准确率, 增强了算法整体的稳定性, 从而提高了处理Argo剖面监测数据的时效性。

1 DBIRCH算法原理及实现

1.1 BIRCH算法

利用层次方法的平衡迭代规约和聚类方法, 简称BRICH(Balanced Iterative Reducing and Clustering Using Hierarchies)算法[7]。它是一种使用聚类特征(CF： Clustering Feature)归纳数据集中各元素间所包含的数字特征, 并根据特征建立链状树形结构聚类特征树(简称CF树: Clustering Feature Tree), 最终通过特征树对数据进行聚类分析的方法。BRICH算法[8]是为大量数据集设计的一种层次聚类方法。因其数据存储结构方式是类B-树的平衡树结构, 因而在数据的插入、删除、遍历、合并及数据分簇等操作均有相当高的执行效率, 故广泛应用于各类大规模高响应数据的聚类分析中[9]。

1.2 问题分析与DBIRCH算法的提出

BIRCH算法因其不保存任何数据点, 仅存储树形结构及聚类特征信息实现压缩数据的效果, 节省了数据信息所占内存空间[10]。但算法聚类过程需限制叶节点及非叶节点的元项个数, 易导致聚类结果与真实数据分布情况偏差较大。且因算法聚类需对数据集进行分层建树, 因此无法处理非凸数据集, 既不能发现非球状簇, 其结果易为链状, 同时在处理高纬度数据时CF特征较难统计。鉴于上述BIRCH算法存在的缺点, 笔者通过一种基于DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法的密度相连关系对BIRCH算法进行改进, 在保证算法时间复杂度不增加的情况下同时提升算法处理非凸数据集的准确率。

1.3 DBIRCH算法相关定义

DBIRCH算法借鉴了DBSCAN算法中密度核心点及密度相连关系等相关思想, 在BIRCH算法构建CF树阶段根据不同的核心邻域建立多棵CF树。同时改进了传统算法的聚类特征CF的定义, 使算法自动更新空间阈值T, 算法在保留了BIRCH算法时间复杂度较低的优点同时可发现任意形状簇, 提高了算法的整体效率及准确度, 其中DBIRCH算法的相关定义如下。

定义1 核心邻域。在以任意样本p为圆心, 空间阈值T为半径的领域内, 存在n个样本点, 当样本点个数n与空间阈值T的比值大于最大阈值系数ω, 既n/T>ω时, 则以样本点p为中心的邻域S为核心邻域。

定义2 非核心邻域。在一个以空间阈值T为半径的邻域内包含n个样本点, 当空间阈值与样本点个数比例小于阈值系数ω, 既n/T<ω时, 则称该邻域为非核心邻域。

定义3 密度相关核心邻域。当两个邻域S1与S2间距离小于一个最小阈值(本节规定为核心的直径即2倍空间阈值T), 即dist(S1,S2)<2T时,S1与S2为一对密度相关核心邻域。

定义4 密度阈值聚类特征(DCF: Density Clustering Feature)。在DBIRCH算法中共有两种不同的聚类特征, 其中, 非叶节点的聚类特征与传统的CF相同, 是由一个三元组{N,LS,SS}表示, 叶节点的聚类特征则引入一个基于密度的空间阈值修正因子, 组成一个新的四元组, 表示为DCF={N,LS,SS,dt}, 其中dt表示当前邻域的阈值修正因子。

定义5 空间阈值修正因子。在叶节点的聚类特征中, 阈值修正因子表示当前邻域内的所有样本点个数n与数据样本的比值自加1后的倒数, 即dt=1/(1+n/N), 用于适应各邻域内不同密度下的空间阈值。

1.4 改进算法

DBIRCH算法根据不同样本所属的核心邻域构建多棵CF树, 并试图吸收合并非核心邻域中元素, 最终通过密度相连关系合并核心邻域生成的CF树达到聚类效果, 解决了算法不能处理非凸数据集的问题。同时引入一种全新的叶节点聚类特征DCF, 并根据不同CF树所属邻域及当前邻域的密度阈值修正因子, 动态适应不同密度邻域的空间阈值T, 从而使算法的聚类质量不在依赖空间阈值参数。

DBIRCH算法过程示意图如图1所示。BDRICH算法共分为3个阶段, 在聚类的第1阶段, 将数据集所有元素依据密度关系分别标记为核心邻域及非核心邻域, 若核心邻域间存在密度相邻情况, 则合并核心邻域为密度相关核心邻域。

在第2阶段中算法分别在不同的核心邻域, 非核心邻域及密度相关核心邻域内根据样本的相应聚类特征构建不同的CF树, 每个CF树中的叶节点内包含各自所属邻域的不同密度阈值修正因子, 并通过全局的空间阈值与密度阈值修正因子的成绩确定当前邻域中的子空间阈值。

第3阶段, 扫描所有非核心邻域中CF树的叶子结点寻找在更新子空间阈值后可以与核心邻域CF树合并的元项, 并将其插入核心CF树中。同时寻找是否有不属于核心邻域的元素能插入非核心邻域CF树中。当一个非核心邻域内元素发生改变则判断该非核心邻域是否满足核心邻域条件, 即n/T>ω, 若满足则将该非核心邻域标记为核心邻域, 并尝试与其他核心邻域CF树合并。当合并完成后, 输出该核心邻域CF树中所有叶子结点的元素集合为最终聚类结果, 非核心邻域树的叶子结点的样本则被标记为噪声点。DBIRCH算法的核心便是基于密度相连思想合并CF树及根据密度阈值修正因子动态改变不同邻域中的子空间阈值, 从而在不改变BIRCH算法时间复杂度的同时利用密度思想发现任意形状簇, 从全局上提升了算法的聚类算法的准确性及鲁棒性。

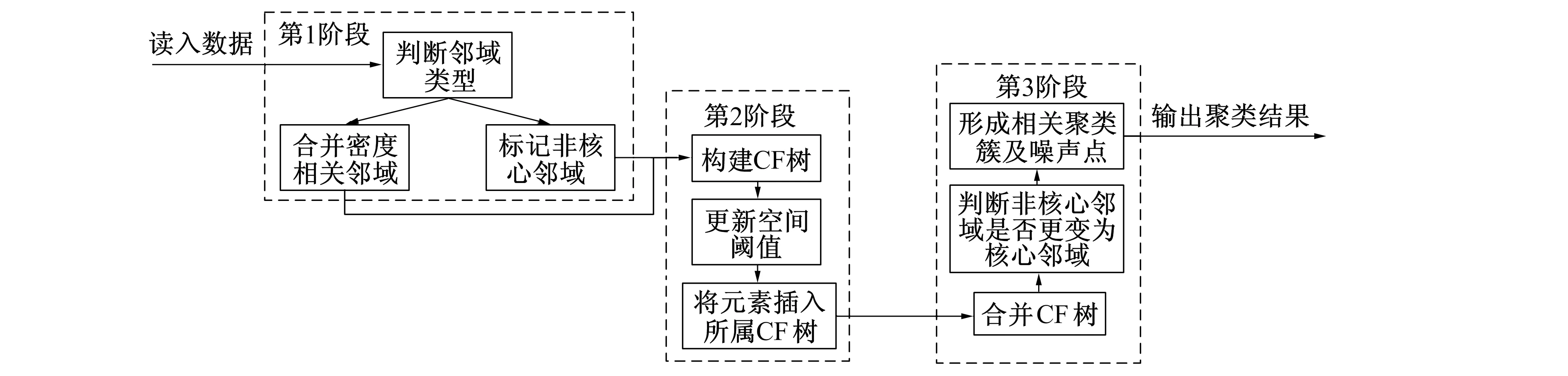
图1 DBIRCH算法过程示意图Fig.1 DBIRCH algorithm process diagram

1.5 DBIRCH算法流程

DBIRCH算法共分为3个阶段, 其算法详细流程如图2所示。

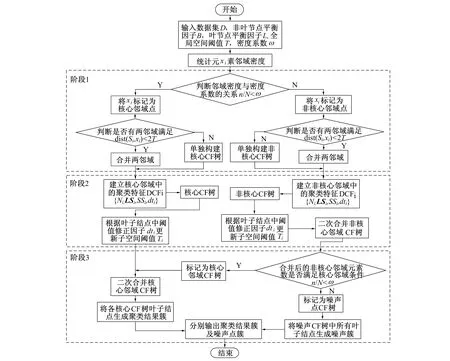
图2 DBIRCH算法流程图Fig.2 DBIRCH algorithm flowchart

输入： 数据集D={x1,x2,x3,…,xn}, 非叶节点平衡因子B, 叶节点平衡因子L, 全局空间阈值T, 密度系数ω。

输出： 核心邻域CF树叶子结点集合S={S1,S2,S3,…,Sk}为聚类结果簇, 非核心邻域CF树叶子结点集合Ω={Ω1,Ω2,Ω3,…,Ωm}为噪声点。

1) 第1阶段。

建立： 核心邻域S={S1,S2,S3,…,Sk}, 其中Si={x1,x2,x3,…,xn}, 非核心邻域Ω={Ω1,Ω2,Ω3,…,Ωm}, 其中Ωi={x1,x2,x3,…,xn}。

Step1 统计数据集D中所有元素的邻域密度, 判断其邻域类型。

If：xi满足邻域密度n大于密度系数ω, 即n/N>ω,xi为核心样本点。

If：S1,S2,S3,…,Sk中存在核心邻域Si与xi满足dist(Si,xi)<2T。

将样本插入Si中,Si=(Si∪xi)。

Else：xi不属于任何核心邻域样本集, 将xi插入一个新的核心邻域样本集中,Si+1={xi}。

Else：xi为非核心样本点。

If：Ω1,Ω2,Ω3,…,Ωm中存在非核心邻域Ωi与xi满足dist(Ωi,xi)<2T。

将样本插入Ωi中,Ωi=(Ωi∪xi)。

Else：xi不属于任何非核心邻域样本集, 将xi插入一个新的非核心邻域样本集中,Ωi+1={xi}。

Step2 若有两核心邻域样本集满足密度相关关系则合并两核心邻域。

If： ∀Si,Si∈S1,S2,S3,…,Sk, 且dist(Si,Sj)<2T。Si,Si为一对密度相关核心邻域,Si={Si∪Sj},Sj=Ø。

2) 第2阶段。

建立： 密度聚类特征四元组DCF={DCF1,DCF2,DCF3,…,DCFn}, 其中DCFi={Ni,LSi,SSi,dti}, 子空间阈值{T1,T2,T3,…,Tn}=0。

Step1 ∀Si∈S1,S2,S3,…,Sk, 统计Si中聚类特征DCFSi={NSi,LSSi,SSSi,dtSi}, 扫描Si={x1,x2,x3,…,xn}, 根据CF树构建方法将元素依次插入CF树各节点中, 生长核心邻域Si内的核心CF树。

Step2 ∀Ωj∈Ω1,Ω2,Ω3,…,Ωm, 统计Ωj中聚类特征DCFΩj={NΩj,LSΩj,SSΩj,dtΩj}, 扫描Ωi={x1,x2,x3,…,xn}, 根据CF树生长方法将元素依次插入CF树各节点中, 构建非核心邻域Si内的核心CF树。

Step3 根据各CF树中叶子结点内存放的密度阈值修正因子dt, 更新各邻域内CF树生长约束条件子空间阈值Ti,Ti=Tdti。

3) 第3阶段。

Step1 扫描S={S1,S2,S3,…,Sk}中所有核心样本集中各CF树的叶子结点内所有元项与Ω={Ω1,Ω2,Ω3,…,Ωm}中所有非核心样本集中各CF树的叶子结点内所有元项, 根据Si邻域核心CF树中更新后的子空间阈值Ti, 判断是否存在∀xi∈Ωi(Ω1,Ω2,Ω3,…,Ωm)属于核心邻域CF树内。

If：xi∈Ωi, 且dist(Si,xi)<2Ti, 则将xi依次从每棵核心CF树的根节点起, 由上至下寻找最近的叶节点, 样本xi插入核心CF树中,Si={Si∪xi}。

Step2 扫描{Ω1,Ω2,Ω3,…,Ωm}中是否存在两非核心样本集的CF树满足更新后的子空间阈值, 若存在, 合并两CF树, 同时更新合并后的非核心CF树内叶子节点元素个数。

Step3 非核心领域元素个数发生变化, 判断其是否满足核心邻域条件。

If： 在Ωi={x1,x2,x3,…,xn}中,n/N>ω则将Ωi标记为核心邻域,Ωi对应CF树标记为核心CF树, 即Sk+1=Ωi,Ωi=Ø。

Else：Ωi被标记为噪声点集,Ωi中所有元素均为噪声点。

2 实验结果与分析

为验证改进后的DBIRCH算法相较其他方法在处理Argo监测数据的具体性能指标包括时间复杂度、聚类准确率及运算速率等, 笔者分别选取测试数据集与真实数据集两类不同的实验数据对传统DBSCAN及传统BIRCH算法在相同的实验环境下进行试验分析, 并根据相同的评价指标判断改进算法与传统算法的整体性能差异。

2.1 实验设计

使用相同的测试集及试验环境对3种不同方法进行测试实验。实验环境为： 处理器IntelR CoreTMi7-8750H, 内存16 GByte, 开发环境为Spyder, Python版本3.6.4, Matlab 2012b。为更直观地反映出DBIRCH算法与传统DBSCAN及BIRCH算法间的性能差异, 该实验首先使用了一组二维的测试集对算法从准确度及运算时间两方面进行实验分析, 从而得出较为客观的实验结果。测试集DATA来自Chameleon公开测试数据集, 由一组含有8 000个样本向量及密度相通的6个非凸形状类簇组成, 同时数据内包含较多的噪声点。因而从数据量和数据复杂度而言均能有效的测试出算法的综合性能。

2.2 算法评价指标

采用两种不同的评价指标对3种不同的算法进行性能评估。首先利用纯度指标对运算结果进行评估, 得出聚类结果簇中正确簇的比重, 而后引入一种新的聚类评价指标兰德系数(RI: Rand Index,RRI), 对结果簇的类间相似度进行评价, 其大致原理如下

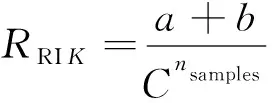
(1)

其中K表示聚类后的结果簇,C表示数据集实际簇,a表示在C与K中均被标记为同一簇的样本对数,b表示C与K中被标记为不同簇的样本对数,Cnsamples表示数据集内所有元素能组成的元素对数。兰德系数RRI的最终结果落在区间[0,1]内, 当RRI无限逼近1时, 说明聚类结果簇间不相似度极高且与实际类簇吻合, 既聚类准确度较高; 反之当RRI无限逼近0时, 则表示聚类结果簇间极为相似, 聚类准确率较低。

2.3 聚类结果分析

使用二维数据集DATA为测试集, 分别对DBIRCH、DBSCAN及BIRCH算法进行多次试验。实验中DBSCAN在聚类前需人工设定参数Minpts及Eps, 同时BIRCH算法及改进的DBIRCH算法也均在聚类初期设定相关初始参数, 因而3种算法在参数选取方面优劣度持平, 但DBIRCH算法对初始参数空间阈值仅做参考, 因此对参数的依赖性没有其他两种算法高。为更加客观地得出有参考价值的实验数据, 实验参数的取值如表1所示。

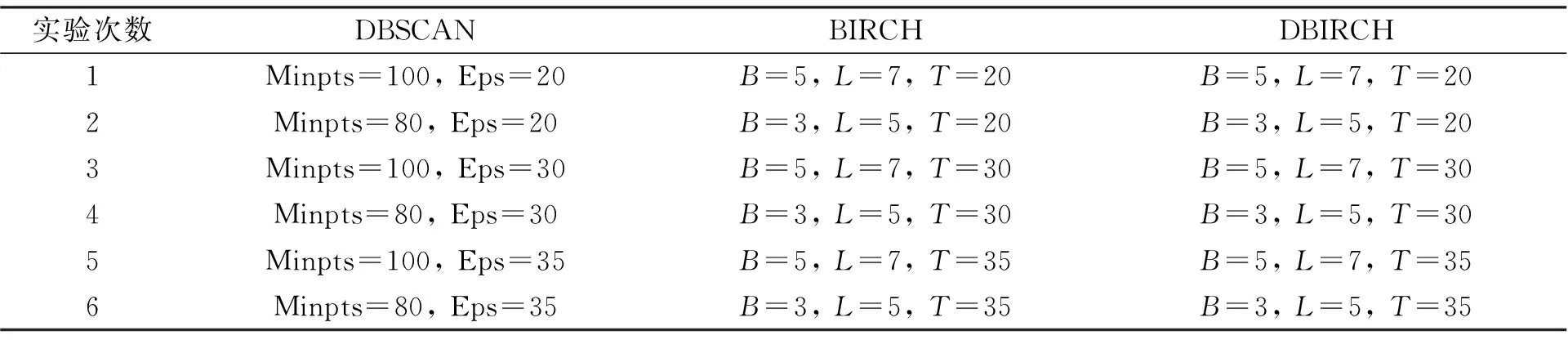
表1 实验参数取值

测试实验选取多组不同参数, 在不同情况下进行了3种算法的对比实验, 并选取了其中最具代表性的结果, 使用Matlab工具绘制出相应的Scatter图, 从而直观地反映出算法的准确率。

DATA测试集由多个形状复杂且密度较高的类簇及大量噪声点组成, 因此算法在处理过程中可能会因数据集的单调性、样本密度差异、噪声点及样本倾斜分布影响聚类效果, 聚类结果如图3～图5所示。

可观测出数据集大体包含6个类簇, 其中黑色“*”表示数据集中的噪声点, 如图3所示, BIRCH算法在处理数据时由于不能较好地发现非凸形簇, 同时对空间阈值T的多度依赖, 导致将6个非凸簇分成多个较小的类簇, 同时各簇间的由噪声点组成的连接线也被标记为结果簇, 故肉眼可见的BIRCH算法在处理该测试集时效果不佳。如图4所示, DBSCAN算法由其原理是根据密度相连关系导出相关簇, 因此发现了数据集中的不同形状簇, 且DBSCAN算法能密度关系标记出噪声点, 但算法对Eps、Minpts等密度相关参数有所依赖, 且数据集内6个类簇间均由密度较高的噪声点相连, 故DBSCAN算法因相连密度点错误地将其中两个不同类簇标记为同一类簇, 此外, 由于类簇边缘存在部分噪声点密度较高的情况, 因此DBSCAN算法生成的结果簇吸收了较多的边缘噪声点。如图5所示, 笔者提出的基于密度思想的改进算法DBIRCH则反映出了较好的聚类效果, 虽然有部分簇间高密度噪声数据被误标记为聚类结果簇, 但算法基本清晰地识别了数据集中6个不同形状簇, 同时对噪声点的标记率也较为良好。因为从全局层面分析, 改进的DBIRCH算法在聚类准确率上优于其他两种传统算法。

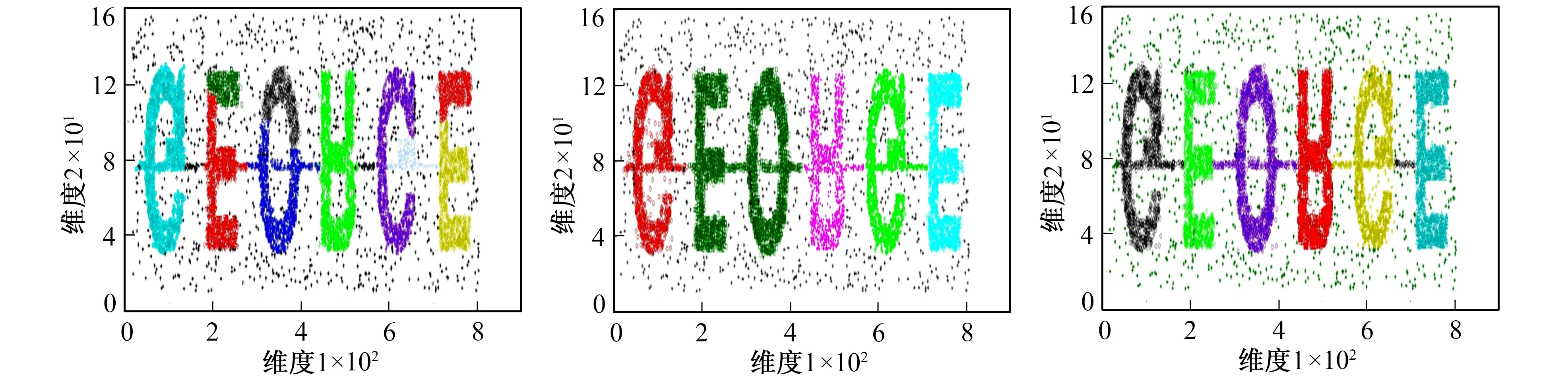
图3 BIRCH算法聚类结果图 图4 DBSCAN算法聚类结果图 图5 DBIRCH算法聚类结果图 Fig.3 Clustering results of birch Fig.4 Clustering result graph Fig.5 Clustering results of algorithm of DBSCAN algorithm dbirch algorithm

3 Argo剖面数据聚类实验与分析

3.1 Argo数据集

为测试改进算法在处理Argo剖面监测数据时真实聚类效果, 实验使用Argo实时资料中心(http:∥www.argo.org.cn/)的Argo浮标实时剖面观测资料, 对算法进行性能评估[11]。数据来自多个Argo浮标不同时间段循环观测所采集的包括温度(TEMP)、盐度(PSAL)及压力(PRES)等多种属性的大量实时样本。同时考虑实验环境运算能力有限, 仅截取2018年2月到2019年2月共计15 000余条剖面监测数据对3种不同算法进行对比实验, 其DBIRCH算法聚类结果如图6所示。

图6 DBIRCH算法聚类结果Fig.6 Clustering results of DBIRCH algorithm

3.2 数据标准化处理

为提升聚类分析处理速率及精度, 根据第2节描述方法对Argo剖面数据中多属性变量进行无量纲标准化处理, 其处理数据取值区间收缩至[0,1]内, 处理结果如表2所示。

表2 数据无量纲化处理结果表

由于Argo浮标实时剖面观测资料数据中包含过多的无用属性导致数据集维度过高[12], 最终致使聚类结果不易比对, 较难分析出3种不同算法间在聚类准确性上的性能差异, 同时过多的冗余数据类型会无故导致处理器运算压力过大、实验整体运算时间过长[13]。不利于从时间复杂度上区分出3种算法间的优劣。因此, 笔者采用一种主成分分析(PCA： Principal Component Analysis)的方法对数据进行降维, 因为PCA方法降维后的数据信息丢失率极低, 且处理后的数据结构最接近原始数据, 故选取PCA方法对Argo浮标剖面监测数据进行降维处理过滤掉无关属性[14], 降低了数据的处理难度。

3.3 实验结果

为在实验环境资源有限的条件下客观有效清晰地反映出DBSCAN、BIRCH及DBIRCH 3种不同算法处理Argo浮标剖面实时监测数据时的具体性能[15]。对3种不同算法分别进行多组仿真实验, 并使用纯度(purity)与兰德指数(RRI)两种不同的评价指标对结果进行分析, 并评估算法的聚类准确率, 同时统计出多次试验的运行时间, 以从算法运行效率上对3种算法做出区分。最终得出3种算法间综合性能的优劣性差异, 具体数据如表3所示。

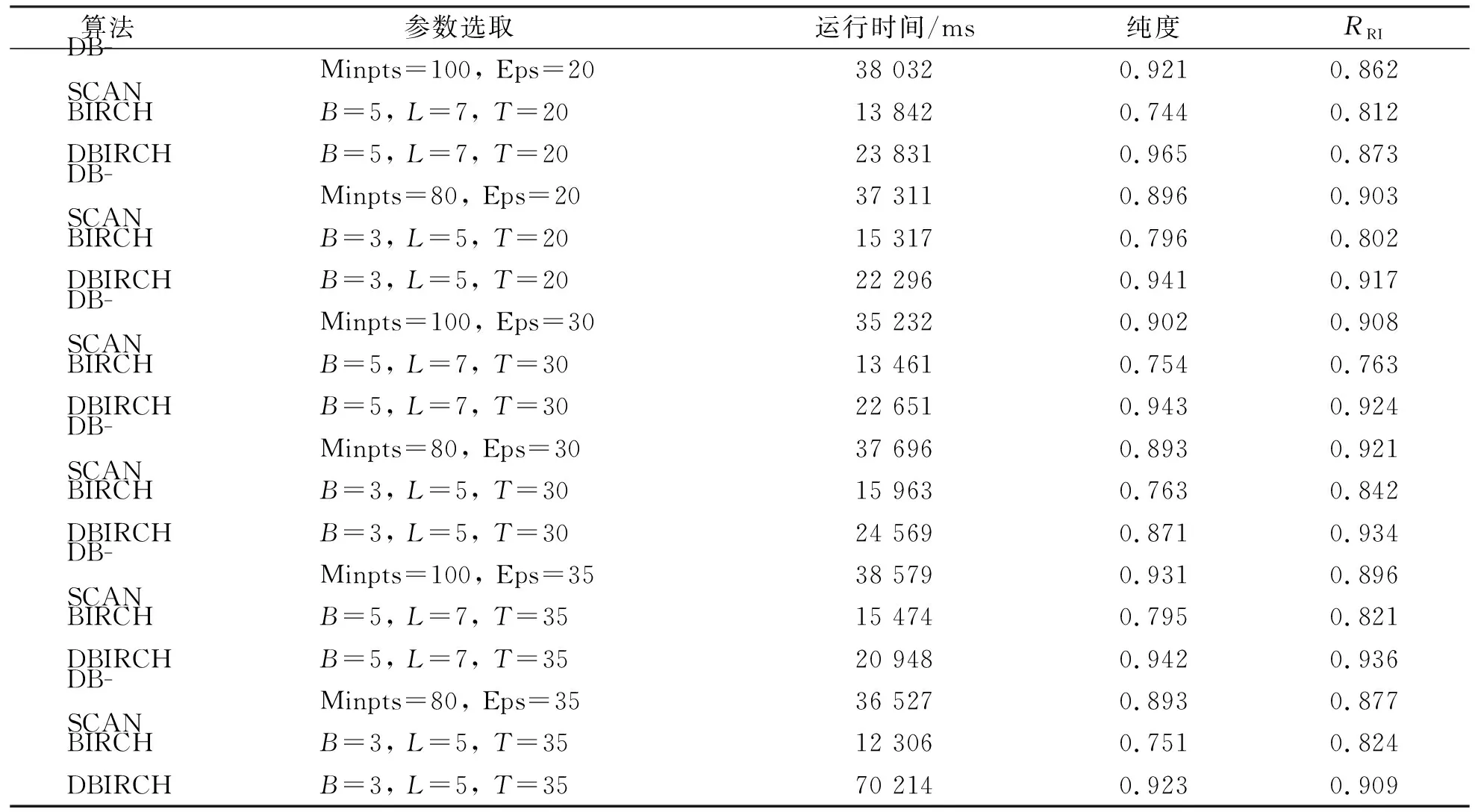
表3 实验结果

依据实验数据分析可知, 在多组不同参数的仿真实验中, 3种算法BIRCH算法预算速率最快, 而从purity与RI指数综合看笔者改进的DBIRCH算法准确率最高。

BIRCH算法因采用构建特征CF树并根据叶子结点输出聚类结果的原理, 导致其不能发现任意形状簇, 从实验数据可以看出, 在3种算法中准确率最低, 但因为BIRCH算法仅需处理数据集的聚类特征, 故运算时间最短。DBSCAN算法则通过密度相连关系导出聚类结果簇, 故能发现任意形状簇, 因此具有较高的聚类性能, 但由于DBSCAN在运算过程需多次计算比较数据集中所有样本间距离, 导致算法需多次遍历数据集, 故而算法的运算时间较长且运算速率较低。笔者改进的DBIRCH算法使用了基于密度聚类的思想构建CF树, 并根据密度相关性输出聚类结果, 虽在运算时间上略慢于BIRCH算法, 但聚类准确率位于3种算法之首。分析可见笔者提出的改进DBIRCH算法在3种不同算法中综合聚类性能最优。

4 结 语

笔者针对Argo浮标剖面实时监测数据的相关特性[16], 引入一种阈值自动修正的DBIRCH算法, 算法基于一种密度阈值的方式标记了核心与非核心邻域, 同时在其中生长一种新的密度聚类特征树DCF-tree, 并依据密度关系将其合并。通过阈值修正因子动态地根据当前邻域样本密度更新BIRCH算法子空间阈值, 并对核心CF树二次合并, 同时输出聚类结果与噪声点。为测试算法的综合性能, 使用测试集与真实Argo浮标剖面实时监测数据集分别根据不同的参数对算法做出多组对比实验, 并使用不同评价指标对算法从运行时间和聚类准确率上进行综合评估, 区分出对比算法间综合性能的优劣性差异。