基于模糊PI有效磁链直接转矩控制系统的研究
2020-11-06
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
0 引言
由于永磁同步电机(permanent magnet synchronous motor,PMSM)有高效率、大功率密度、强过载能力的优点[1],使得其成为轨道交通、数控机床及工业机器人等领域的重要驱动部件。随着电力电子技术和自动控制技术的高速发展,电机应用领域对永磁同步电机的控制性能提出了更高要求,而改进控制方法则是提高永磁同步电机性能的关键任务之一[2]。因此,对永磁同步电机控制方法的研究具有重要意义。
传统的直接转矩控制虽然响应速度快、抗干扰能力和鲁棒性强,但是磁链和转矩脉动较大,在某些低速控制场合下无法精确控制,并且容易产生高频噪声[3-4]。文献[5]介绍了一种采用滑模的磁链观测器,由定子绕组的电压、电流等电机参数观测出α、β坐标系的定子磁链,然后由公式计算出定子磁链和转矩,以此进行直接转矩控制,该方法比较依赖电机参数,在电机运行时不可避免地使定子电阻、d轴电感和q轴电感发生变化,并且传感器检测参数和逆变器开关死区也可能产生误差,这些参数变化在永磁同步电机低速运行时更加明显[6-7]。文献[8]设计了一种基于滑模的直接转矩控制,采用了传统的比例积分控制器(proportional integral controller,PI),但传统PI控制器无法进行参数在线自整定,对时变、非线性等复杂系统控制性能比较差,且存在系统超调量过大、震荡比较严重、转矩脉动抑制不够理想以及系统响应速度慢等缺点。
为减少上述控制中的缺陷,本研究在传统磁链滑模的基础上设计了有效磁链滑模观测器。通过构建有效磁链,使滑模观测器只依赖于定子绕组电阻和交轴电感,省去对直轴电感参数的依赖,消除了PMSM的凸极现象。用模糊PI控制器替代传统PI控制器使系统能够适应不同的环境要求,并通过构建李雅普诺夫函数进行稳定性分析。最后,采用Matlab/Simulink 仿真验证基于模糊PI的PMSM 有效磁链滑模直接转矩控制系统有较强的适应性和鲁棒性。
1 PMSM数学模型
1.1 直接转矩控制数学模型
直接转矩控制通过实时检测PMSM 定子电压和电流,计算出磁链和转矩幅值,然后与给定数值进行比较产生差值,由磁链和转矩调节器产生空间电压矢量进行控制。由于永磁同步电机具有非线性、强耦合、多变量等特点,本研究为了便于对表贴式PMSM 进行数学建模,做出以下假设[9-10]:
1)定子三相绕组对称;2)电机气隙均匀;3)不考虑磁滞、涡流损耗和磁饱和影响。
定子电压在α、β坐标系下的表达式为
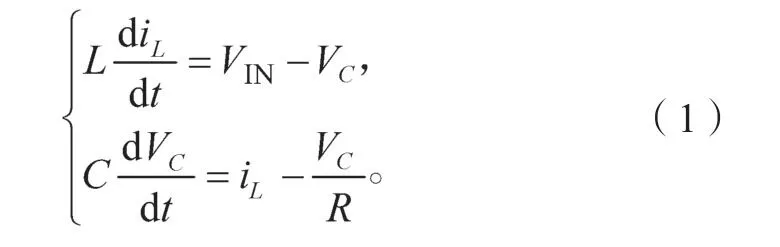
式中:usα、usβ为定子电压在α、β坐标轴的分量;isα、isβ为定子电流在α、β坐标轴的分量;ψsα、ψsβ为定子磁链在α、β坐标轴的分量;Rs为定子电阻。
由式(1)可以推导出定子磁链在α、β坐标轴的表达式为

由磁链在α、β坐标轴的分量可知定子磁链的幅值表达式为

在α、β两相静止坐标系下永磁同步电机的转矩方程表达式为
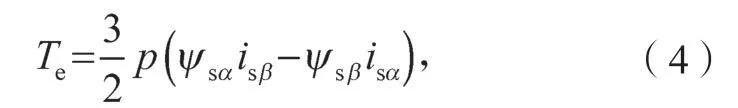
式中:|ψs|为定子磁链的幅值;Te为电磁转矩;p为电机极对数。
1.2 有效磁链滑模观测器设计
有效磁链的表达式为
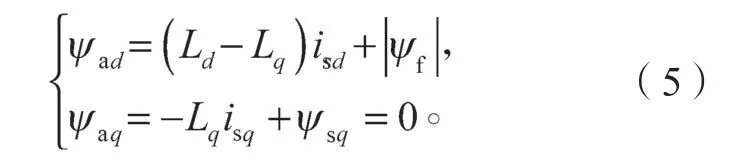
式中:ψad、ψaq分别为d、q轴有效磁链;ψsq为q轴定子磁链;isd、isq分别为d、q轴定子电流;Ld、Lq分别为d、q轴电感;|ψf|为永磁体磁链幅值。
有效磁链ψa在坐标系中与定子磁链ψs和永磁体磁链ψf的关系如图1所示。

图1 磁链关系矢量图Fig.1 Flux linkage relation vector diagram
有效磁链滑模观测器的状态方程需要转子的位置信息,因此可以构建如下定子电流is和有效磁链在α、β坐标系下的状态方程:
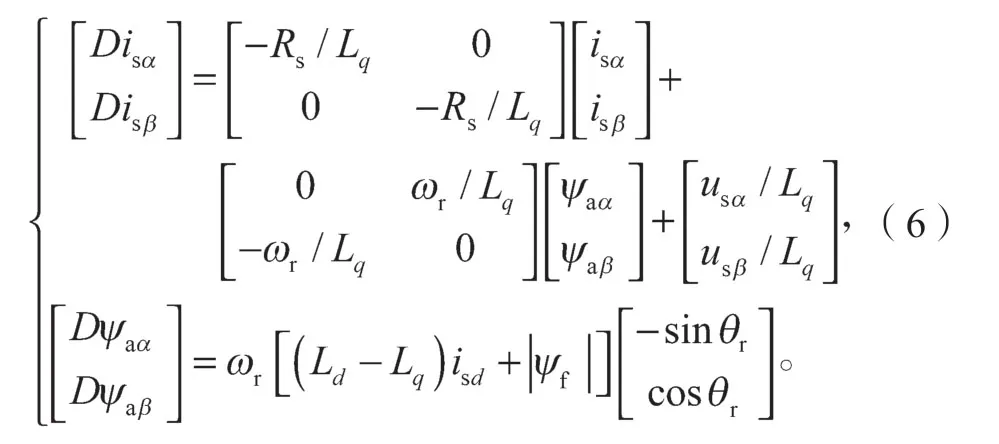
式中:D为微分运算d/dt;ψaα、ψaβ为α、β坐标系下的有效磁链;θr为转子旋转角;ωr为转子机械角速度。
根据式(6),PMSM的定子电流和有效磁链的状态方程可以构建有效磁链滑模观测器,即

1.3 系统稳定性分析
滑模运动要求能够趋近于切换面s=0,通过构造李雅普诺夫函数V对有效磁链滑模观测器进行稳定性分析,若<0,则满足稳定性要求,李雅普诺夫函数V与切换面s的关系由下式构成:
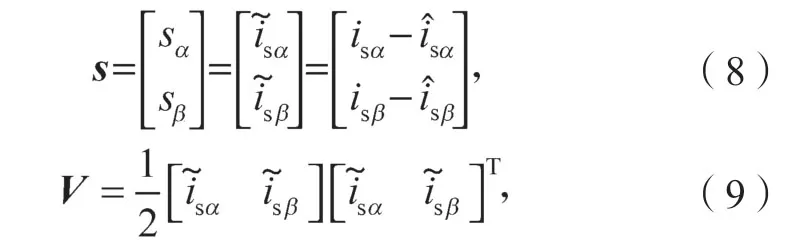
根据公式(6)(7)可以得到电流观测误差为
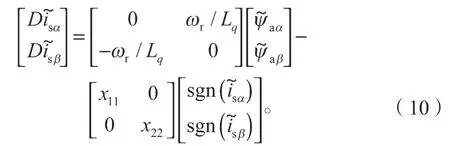
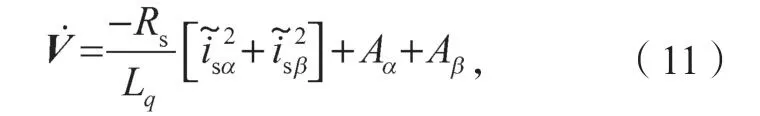
式中:Aα、Aβ分别为

由式(11)可知,如果要满足系统的稳定性要求,只需要Aα+Aβ<0,则<0。根据符号函数的取值范围对电机参数的常数矩阵x分开进行讨论,可以得出:
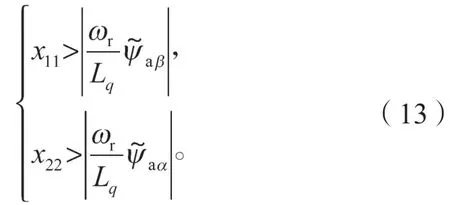
由电流观测误差公式(10)可以得到:
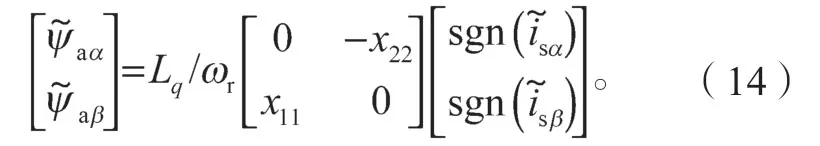
将式(6)(7)求差可得有效磁链的观测误差:
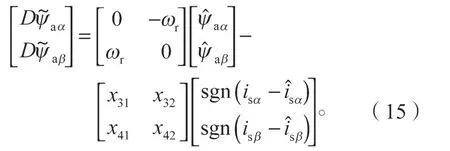
对式(15)的电机参数常数矩阵进行化简,使x31=-x11Lq,x42=-x22Lq,然后结合式(14)(15)求得有效磁链观测误差的动态方程:
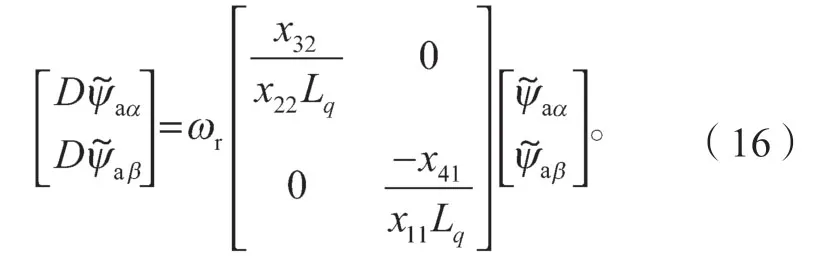
上述证明可推导出滑模观测器的充分条件如下:

2 模糊PI控制器的设计
2.1 模糊PI基本原理
模糊PI控制器采用模糊数学的方法将控制规则和条件用模糊集合表示出来,然后将相关信息存储在计算机知识库中[11]。在系统响应时,根据控制变量的误差和变化率进行模糊化处理,由计算机存储的规则处理后将输出进行解模糊,然后将解模糊的输出结果输送至被控对象[12]。模糊控制规则一般是专家通过大量实验和经验总结得出,在整个系统运行过程中实验者无法对其进行查看,只能根据其变化率和输出结果进行分析[13-14]。模糊控制系统组成如图2所示。

图2 模糊控制器基本组成图Fig.2 Basic composition diagram of fuzzy controller
本研究建立的模糊PI控制结构原理如图3所示。将模糊算法与PI控制器进行结合得到模糊PI控制器,图中in为输入信号,通过将系统误差e和误差变化率ec输入至模糊推理过程中获得ΔKp、ΔKi作为PI参数的修正量,然后对PI参数进行在线调节。
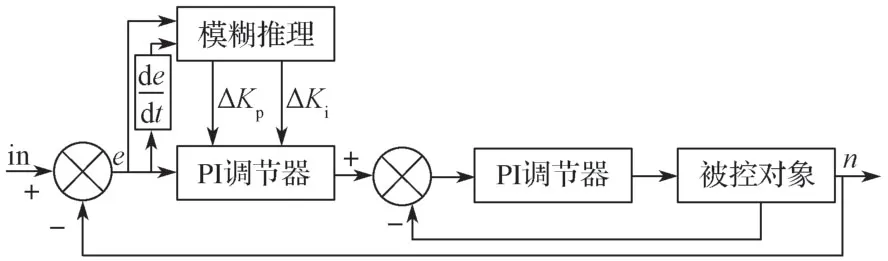
图3 模糊PI控制基本原理图Fig.3 Fuzzy PI basic control schematic diagram
2.2 模糊PI控制规则
本设计的模糊PI控制器隶属函数采用了三角函数和S形函数的组合来描述,使用7个语言模糊集表示系统误差e、误差变化率ec和输出变量ΔKp、ΔKi,分别为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大),输入变量、输出变量的论域均为{-3,-2,-1,0,1,2,3}。采用误差逐级逼近的方式设置ΔKp、ΔKi参数,通过将模糊PI控制器应用于系统的转速环实现PI参数的在线自整定。模糊控制规则见表1~2。
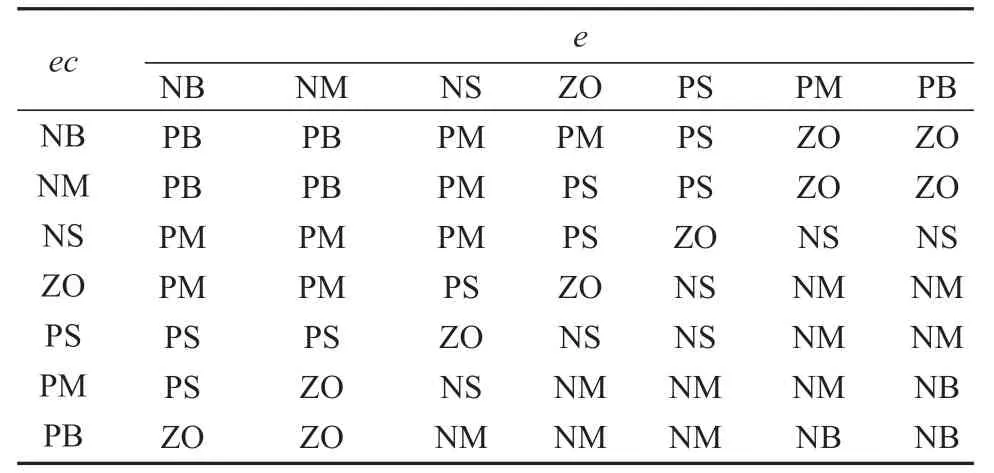
表1 ΔKp的模糊控制规则表Table1 Fuzzy control rule table of ΔKp

表2 ΔKi的模糊控制规则表Table2 Fuzzy control rule table of ΔKi
2.3 模糊控制过程
根据Mamdani 模糊推理机制和centroid 反模糊法得到输出变量ΔKp、ΔKi,然后与初始值叠加可以得到控制器的参数调节公式:

3 系统仿真
3.1 系统仿真模型
图4为基于模糊PI的有效磁链直接转矩控制系统仿真模型。由图4可知,采用速度环作为控制系统的外环,通过模糊PI控制器实时改进变量ΔKp、ΔKi进行PI参数在线修正,然后由模糊PI 输出电磁转矩给定值,电磁转矩误差经过转矩滞环输出到PWM 脉冲发生器;定子磁链通过有效磁链算法进行观测,将观测值与给定值比较产生的偏差经过磁链滞环输出到PWM 脉冲发生器;系统中采用S函数对磁链所在扇区的位置编号进行计算,然后输出系统最优开关矢量对开关管进行控制。

图4 基于模糊PI的有效磁链直接转矩控制仿真模型Fig.4 Simulation model of effective flux direct torque control based on fuzzy PI
式(18)(19)中:Kp(0)、Ki(0)表示PI参数初始值;Kp、Ki表示修正后的PI参数。
电机参数设置如下:额定功率P=1 kW,d轴电感Ld=0.008 5 H,q轴电感Lq=0.008 5 H,定子电阻Rs=1.2 Ω,转动惯量J=0.008 kg·m2,转子磁链ψf=0.175 Wb,极对数p=4。
3.2 仿真结果分析
实验中通过两个调速方案对比的形式进行论证,由于传统磁链滑模观测器在低速状态下观测磁链效果较差,且无法进行精确控制,因此两个方案都在60 r/min的低速状态下空载运行,在0.15 s时突加1.5 N·m的负载,实验仿真时间为0.4 s。
1)传统PI控制器结合传统磁链滑模控制结果
图5所示为低速状态下传统PI控制器的磁链滑模直接转矩控制结果。由图5可以得知,定子磁链波形显示在0.003 6 s 磁链观测器开始跟踪磁链,在0.3 Wb的给定磁链下,其磁链观测值在0.185~0.238 Wb之间波动,且明显无法进行正常的磁链观测;转速波形显示在给定60 r/min的转速度下,超调最大值达30%,在0.025 s系统进入稳定转速,系统突加负载时,在0.017 s内系统恢复稳定;转矩波形显示在0.15 s时突加1.5 N·m 负载能够在0.001 5 s 内达到稳定状态,但转矩波动明显,转矩观测值在0.83~2.10 N·m之间波动。

图5 传统PI控制器结合传统磁链滑模控制结果Fig.5 Results of traditional PI controller combined with traditional flux slip mode control
2)模糊PI控制器结合改进磁链滑模控制结果
图6所示为低速状态下模糊PI控制器的改进磁链滑模直接转矩控制结果。
由图6可知定子磁链波形显示在0.003 2 s 磁链观测器开始跟踪磁链,在给定0.3 Wb 磁链下,其磁链观测值在0.298 0~0.300 5 Wb之间波动;转速波形显示低速状态下超调得到抑制,在给定60 r/min 速度下,超调最大值为5%,在0.018 s系统进入稳定转速,系统突加负载时,在0.16 s 内系统恢复稳定;转矩波形显示在0.15 s时突加1.5 N·m 负载能够在0.000 8 s内达到稳定状态,转矩观测值在1.39~1.70 N·m之间波动。
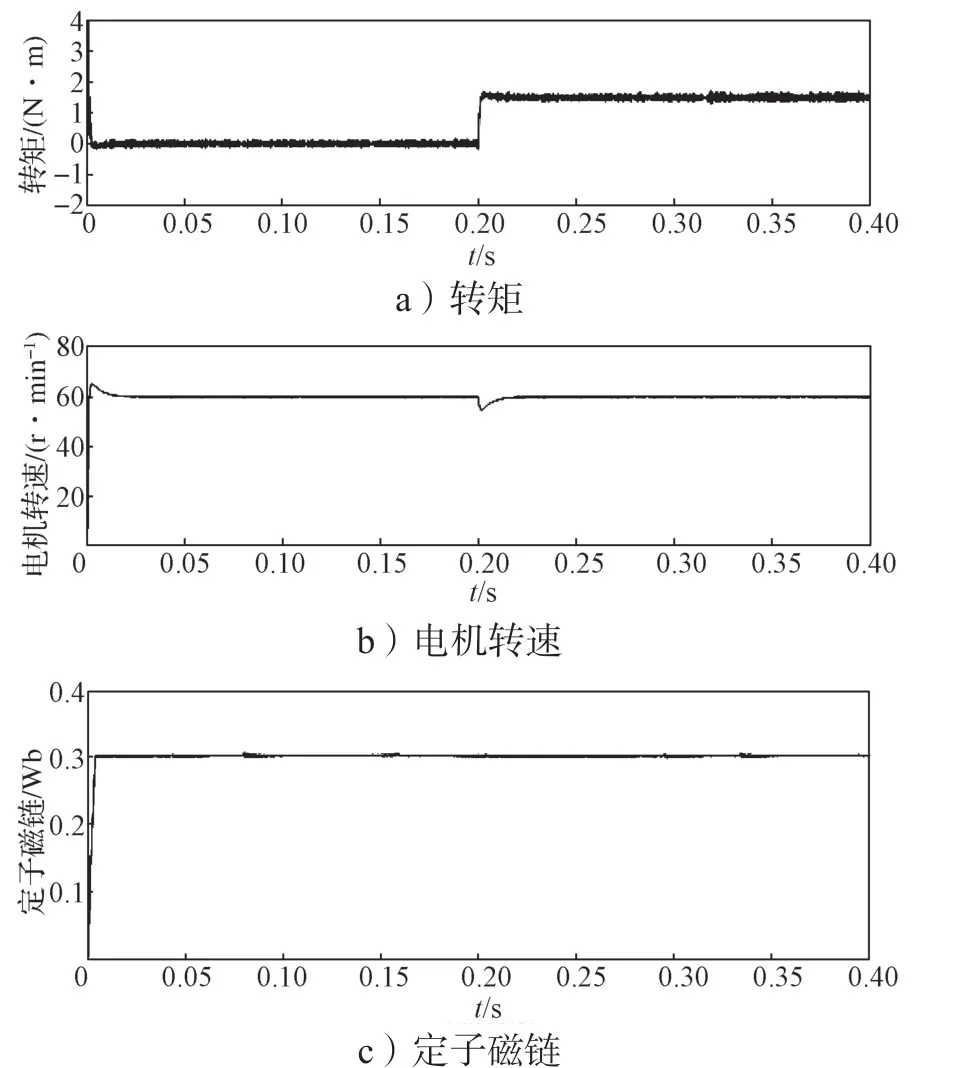
图6 模糊PI控制器结合改进磁链滑模控制结果Fig.6 Fuzzy PI controller combined with improved flux sliding mode control results
3)传统PI控制器结合传统磁链滑模控制的电机参数适应能力仿真结果
图7所示为传统PI控制器结合传统磁链滑模直接转矩控制系统对电机参数抗扰动能力的仿真结果。电机定子电阻初始设定为1.2 Ω,在低速状态下由于电阻发热使电机参数发生变化,因此仿真模型中设定变化后的定子电阻为2.2 Ω,由转速波形显示可知,当电机参数发生变化后,转速波形振荡严重,在0.282~0.328 s时出现无法正常跟踪设定速度的情况,表现出传统控制方法存在对电机参数适应能力不强的结果。


图7 传统控制方法对电机参数的适应能力Fig.7 Adaptability of traditional control methods to motor parameters
4)模糊PI控制器结合改进磁链滑模控制的电机参数适应能力仿真
图8所示为模糊PI控制器结合改进磁链滑模直接转矩控制系统对电机参数抗扰动能力的仿真结果。

图8 改进后的控制方法对电机参数的适应能力Fig.8 Adaptability of the improved control method to the motor parameters
电机定子电阻初始设定为1.2 Ω,参数发生变化后的定子电阻为2.2 Ω,由参数变化前后的转速波形可知,定子电阻变化对转速影响甚微,表示这种控制方法对电机参数变化具有很强的适应能力。
5)两种控制方法仿真结果对比分析
由两种PMSM控制方案仿真结果对比分析可知,永磁同步电机采用传统PI控制器结合传统磁链滑模直接转矩控制方法,存在定子磁链和转矩脉动较大、抖振明显、系统对电机参数变化的适应能力不强的缺陷,低速状态下在0.15 s时突加负载时系统转速能够较快回到预设值,但在启动初期超调量较大,在到达预设值之后存在明显的震荡。而采用模糊PI控制器结合有效磁链直接转矩控制方法,定子磁链得到十分明显的抑制,抖振现象变小,系统对电机参数变化时的适应能力得到加强,相对于传统PI控制器,系统在启动初期超调过大的现象得到改善,表示该系统响应比较快,并且震荡问题也得到了一定的缓解。但转速突加负载表现出的结果表明其抗干扰能力和抖振抑制仍然还有很大的改进空间。
4 结语
本文在传统PI控制器的磁链滑模直接转矩控制系统的基础上,应用模糊理论和有效磁链滑模观测器重新设计了永磁同步电机直接转矩控制系统。由仿真结果可知,采用有效磁链滑模算法作为观测器,可以有效地抑制传统磁链滑模作为观测器存在的转矩脉动大的问题,且减少系统对电机参数的依赖,具有良好的静态和动态特性。采用模糊PI控制解决了传统PI控制对参数扰动适应能力不强的缺陷,增加了系统的响应速度和鲁棒性。本课题为后续对永磁同步电机控制的研究指明了方向。
