基于双随机相位编码的局部混合光学加密系统*

许祥馨 常军† 武楚晗 宋大林

1) (北京理工大学光电学院, 北京 100081)

2) (公安部第一研究所, 北京 100044)

1 引 言

随着信息化社会的发展, 信息安全已经成为了一个热门的研究方向. 由于光学技术对于信息安全的显著优势, 光学加密技术成为了近年来重要研究热点之一. 自从1995年Refregier和Javidi[1]提出基于4f系统的双随机相位编码(DRPE)技术以来, 光学加密技术开始得到越来越多的研究[2−12].

由于基于4f系统的DRPE技术是最先提出的, 所以后续的很多研究都是以DRPE技术为基础展开的[8−12]. 其中, 在 2004 年, 针对 4f系统中两块随机相位板的纵向位置无法作为密钥的问题, 司徒国海等[9]提出了基于菲涅耳衍射的DRPE系统.在该系统中, 衍射距离和照射光的波长都可以作为系统的密钥, 且系统不需要透镜, 既简化了系统又提高了系统的安全性. 受此启发, 越来越多的加密系统在菲涅耳衍射的基础上展开研究[13−17].

上述提到的加密方法都是对整体图像进行无差别的加密, 但是在实际应用中, 有时不仅需要对图像整体信息进行隐蔽, 还需要对图像中的重要信息进行选择性加密, 以此来提高局部重要信息的安全性. 如在 2007 年, Xiang 等[18]提出了一种利用时空混沌系统对灰度图像进行加密的通用选择图像加密算法; 在 2011 年, Taneja 等[19]提出了一种有效的小波域选择性加密算法, 该算法只对混沌流密码的有效子带进行加密; 在2012年, Bhatnagar等[20]提出了一种结合了锯齿空间填充曲线、感兴趣像素点、非线性混沌映射和奇异值分解的选择性加密方法; 在2013年, 孔德照等[21]通过研究分数小波变换多层次分解和DRPE技术, 以分数小波变换为基本理论依据, 提出了一种多密钥的选择性光学图像加密系统; 在2017年, 肖宁等[22]提出一种基于多特征差异检测与联合控制映射的红外图像选择算法, 该算法实现了对红外图像的选择性加密. 然而这些方法多数是基于图像处理的图像加密方法, 大多基于电子方式实现, 难以通过光学结构实现, 其实用性受到了限制. 衍射系统结构简单,易于实现, 但是一旦被攻击者破获了衍射距离和衍射波长, 系统便容易受到攻击[23].

针对上述问题, 本文提出了一种基于双随机相位编码的局部混合光学加密系统, 该系统将4f系统和衍射系统相结合, 两个系统同时进行加密, 将产生的两个密文通过局部替换的方式进行混合, 实现了对原始图像中的局部信息进行选择性加密; 该系统采用共孔径、双光路结构, 该结构在光学设计中已被广泛使用, 技术成熟且易于实现, 提高了选择性光学加密系统的实用性.

2 基于DRPE的局部混合光学加密系统

2.1 加密过程

基于DRPE的局部混合光学加密系统结构如图1所示. 该系统包含两个通道, 4f系统作为被选择信息加密通道, 衍射系统作为未被选择信息加密通道. 当原始图像经过随机相位1(RPM1)的调制后, 由选择性分光镜通过反射和透射将光分为两部分, 选择性分光镜为局部镀有反射膜的薄透明玻璃板, 薄透明玻璃板带来的相位延迟可以忽略不计.经过分光镜反射的光进入4f系统中, 其中, RPM1到透镜1的光程为f. 这部分光在4f系统的频域处受到随机相位2(RPM2)的被选择部分(图1中RPM2的斜线部分)调制, 经过透镜2得到加密图像φ4f,φ4f就是原始图像中被选择的局部信息对应的加密图像. 经过分光镜透射的光进入到衍射系统中, 经过一次衍射距离为2f的衍射后被RPM2调制, 再经过一次衍射距离为2f的衍射后得到加密图像φdif. 将图1中通过衍射系统得到的加密图像φdif中的斜线部分用φ4f替换, 得到最终的加密图像φ. 其中,φ4f和 RPM2中的被选择部分与φdif中被替换的部分尺寸相同.

系统的加密流程图如图2所示, 其中 F T{·}和FT−1{·}分别代表的是傅里叶变换和逆傅里叶变换;FST2f{·}代表的是进行一次衍射距离为2f的菲涅耳变换;O4f(x,y) 和Odif(x,y) 分别代表进入 4f系统的图像和进入衍射系统的图像, 也就是被选择性加密的明文和未被选择性加密的明文;P1(x,y) 和P2(x,y)分别代表RPM1和RPM2, 二者互不相关,相位分布范围均为表示图 2 中RPM2中被选择部分;φ4f(x,y) 和φdif(x,y) 分别代表经过4f系统得到的加密图像和经过衍射系统得到的加密图像;φcut(x,y) 代表衍射系统加密图像中被替换掉的部分;φ(x,y) 代表最终的加密图像.

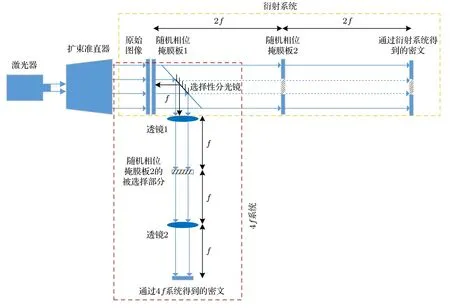
图 1 提出的系统加密部分示意图(f是透镜1和透镜2的焦距)Fig. 1. Schematic diagram of the proposed encryption system (f is the focal length of lens 1 and lens 2).

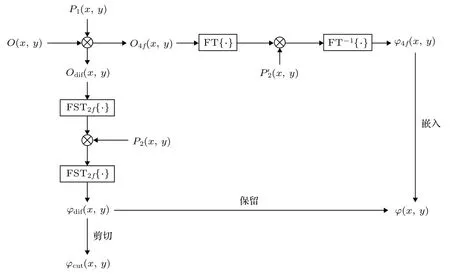
图 2 加密系统的流程图Fig. 2. Flow chart of the encryption system.

4f系统和衍射系统的加密过程分别如(1)式和(2)式所示:

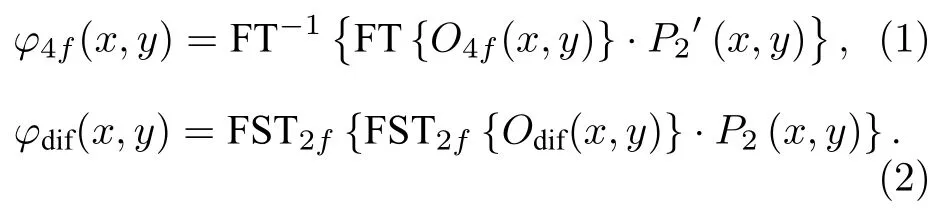
2.2 解密过程

解密过程为加密过程的逆过程. 首先将φ4f(x,y)剪切出来, 通过φ4f(x,y) 得出φcut(x,y) , 就可以 得 出 正 确 的φdif(x,y) .φ4f(x,y) 和φdif(x,y) 分 别经过加密过程的逆过程就可以得到O4f(x,y) 和Odif(x,y), 从而正确地恢复出原始图像, 其流程图如图 3 所示. 其中, F T{·}和 F T−1{·}分别代表傅里叶变换和逆傅里叶变换; F ST−2f{·}代表的是进行一次衍射距离为–2f的菲涅耳变换;K1(x,y) 等于FT{φcut(x,y)}/FT{φ4f(x,y)};K2(x,y) ,分别代表代表P2(x,y) 和的共轭; 通过解密过程得到的是O(x,y)·P1(x,y) , 若O(x,y) 是正实值函数, 则通过CCD等强度探测器件就可以恢复出明文信息O(x,y) ; 若O(x,y) 为复振幅函数, 则还需知道P1(x,y) 的共轭才能正确解密明文信息.

4f系统和衍射系统的解密过程分别如(3)式和(4)式所示:

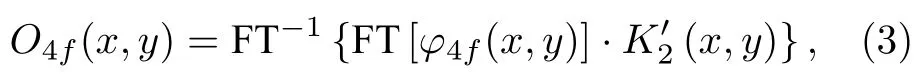
图 3 解密系统的流程图Fig. 3. Flow chart of decryption system.

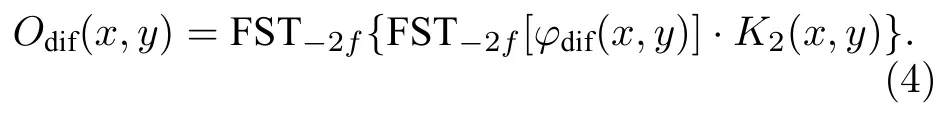
(4)式的实现方式是将衍射加密图像的复共轭函数φ∗dif(x,y)做一次衍射距离为2f的菲涅耳衍射, 经过P2(x,y) 调制后再经过一次衍射距离为2f的菲涅耳衍射, 其过程为

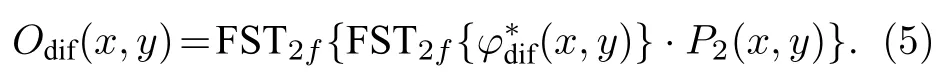
由解密流程图可以看出, 在解密过程中, 不仅需要相位函数K1(x,y) 和K2(x,y) , 以及菲涅耳变换的衍射距离和衍射波长, 还需要知道选择性加密的图像的尺寸大小和位置, 才能完成解密. 选择性加密的图像的尺寸大小和位置增大了密钥空间, 提高了系统的安全性.

3 仿真分析与讨论

3.1 系统的有效性分析

可以通过观察不同加密图像的直方图, 对所提出的加密系统进行统计分析. 通过系统加密的3个图像的原始图像和加密图像的统计特性如图4所示. 从图 4中可以看到, 虽然原图都是不同的, 但是他们加密后加密图像的直方图分布都是瑞利分布. 换句话说, 攻击者不能通过分析加密图像的直方图来获得任何有益的信息, 说明该系统可以有效地隐藏信息.

均方误差(MSE)用来评价图像解密的质量.经过所提出的系统解密后的图像与原图(Lena)的MSE 为 9.2594 × 10–4, 这说明原始图像被很好地还原.

峰值信噪比PSNR被描述为峰值信号与MSE之间的比率. 原始图像和解密图像之间的PSNR值越高, 就说明图像加密方案越有效. 经过所提出的系统解密后的图像与原图(Lena)的PSNR是30.1238 dB, PSNR 大于 30 dB, 说明原始图像被很好地还原.

3.2 系统的密钥敏感性分析

本文提出的系统密钥空间较大, 包括相位函数K1(x,y)和K2(x,y) 、图像剪切的尺寸大小和位置、衍射过程中的衍射距离和波长, 在本节中将依次分析系统对于各个密钥的敏感性. 在分析某个密钥敏感性时, 其他密钥均正确.

图 4 原始图像和加密图像的直方图Fig. 4. Histogram of original and encrypted images.

在仿真过程中, 原始图像的大小是256 × 256,φcut(x,y),φ4f(x,y) 和的大小均为 150 × 150,其 中φ4f(x,y) 就 是 选 择 性 加 密 图 像 ;φcut(x,y) 和的位置均位于所在图像的中心位置,φ4f(x,y)也位于最终加密图像φ(x,y) 的中心位置.

用相关系数(CC)来评价解密图像与原始图像的相关程度, CC越大说明解密效果越好, CC的公式如下所示,O(x,y) 表示原图,OD(x,y) 表示解密后的图像.

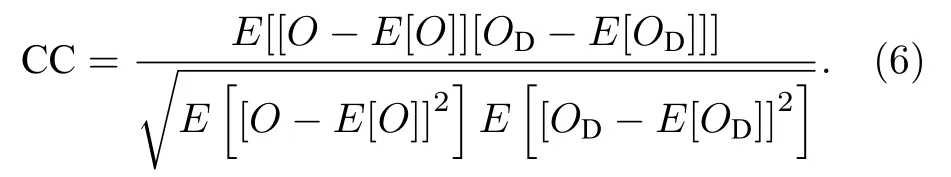
3.2.1 系统对相位函数K1(x,y) 和K2(x,y) 的敏感性分析

相位函数K1(x,y) 的作用是正确还原出φcut(x,y), 得到衍射加密图像φdif(x,y) , 从而恢复出明文信息. 图5显示了当相位函数K1(x,y) 正确和错误时的结果.

由图5可以看出, 无论什么情况下, 被选择性加密的局部区域都可以被还原, 相位函数K1(x,y)只对衍射部分有影响, 因为相位函数K1(x,y) 的作用只有正确还原出φcut(x,y) , 这与上面的分析一致. 而且从图 5的结果中可以看出, 相位函数K1(x,y)的振幅信息对还原图像的质量影响更大,相位函数K1(x,y) 的相位信息对还原图像的质量影响很小. 系统对相位函数K1(x,y) 的相位信息的密钥敏感性的结果如图6所示, 图6中的CC是解密得到的衍射系统图像与Odif(x,y) 之间的相关系数. 当相位函数K1(x,y) 的相位信息错误时, 恢复出来的衍射加密图像中的φcut(x,y) 就会错误,就会导致无法正确的还原出Odif(x,y) , 也就是说φcut(x,y)占φdif(x,y) 的比例越大, 系统就对相位函数K1(x,y) 更敏感, 当φcut(x,y) 的边长大于 160 个像 素 时 , 即φcut(x,y) 占φdif(x,y) 的 比 例 大 于 39%时, 解密得到的衍射系统图像与Odif(x,y) 之间的相关系数小于0.4, 此时认为系统对相位函数K1(x,y)的密钥敏感性较强.

图 5 系统对相位函数 K 1(x,y) 的密钥敏感性Fig. 5. Key sensitivity of the system to the phase function K 1(x,y) .

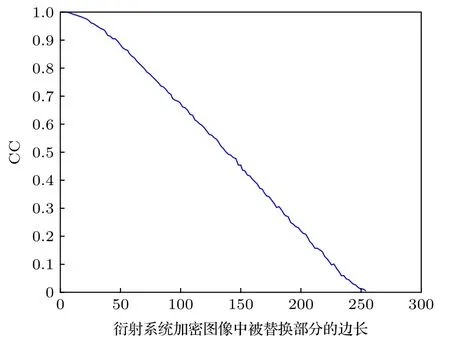
图 6 系统对相位函数 K 1(x,y) 的相位信息的密钥敏感性 与 φ cut(x,y) 大 小 的 关 系Fig. 6. Relationship between the key sensitivity of the system to the phase information of the phase function K1(x,y) and the size of φ cut(x,y) .

另外一个相位函数K2(x,y) 对于衍射系统和4f系统都有影响, 当相位函数K2(x,y) 错误时的解密图像仿真结果如图7所示. 这与之前的研究结果相一致, 4f系统对频域相位函数的密钥敏感性较强. 从图 7 中可以看到, 当K2(x,y) 中正确, 其他相位信息错误时, 可以完美地解密出O4f(x,y), 但是无法解密Odif(x,y) ; 当K2(x,y) 中错误, 其他相位信息正确时,Odif(x,y) 可以被较好的还原, 但是无法解密O4f(x,y) ; 当K2(x,y)完全错误时, 原始图像任何信息都无法被还原.

3.2.2 系统对选择性加密图像的尺寸和位置的敏感性分析

选择性加密图像的尺寸和位置是对局部重要信息加密的重要密钥, 只有知道正确的尺寸和位置才能够正确地剪切出φ4f(x,y) , 并通过φ4f(x,y) 得到正确的φdif(x,y) , 从而正确还原出明文信息. 但是, 在解密时如果图像剪切的尺寸和位置与加密过程不同, 则会对解密图像的质量造成影响. 解密时,若图像剪切的位置正确, 图像剪切的尺寸不同对应的解密图像如图8所示.

由图8可以看出, 在解密过程中, 剪切图像的尺寸错误会对解密图像的质量造成影响, 图9给出了不同剪切图像的尺寸对应的CC.

图 8 图像剪切的尺寸不同对应的解密图像 (剪切图像正确尺寸为 150 × 150) (a) 50 × 50, CC = 0.2272; (b) 150 × 150, CC =0.9934; (c) 250 × 250, CC = 0.0056Fig. 8. Decrypted images for different cropped image sizes (the correct size of the cropped image is 150 × 150): (a) 50 × 50, CC =0.2272; (b) 150 × 150, CC = 0.9934; (c) 250 × 250, CC = 0.0056.

图 9 不同剪切图像尺寸对应的 CC (正确尺寸为 150 ×150)Fig. 9. CC for different cropped image sizes (correct size is 150 × 150).

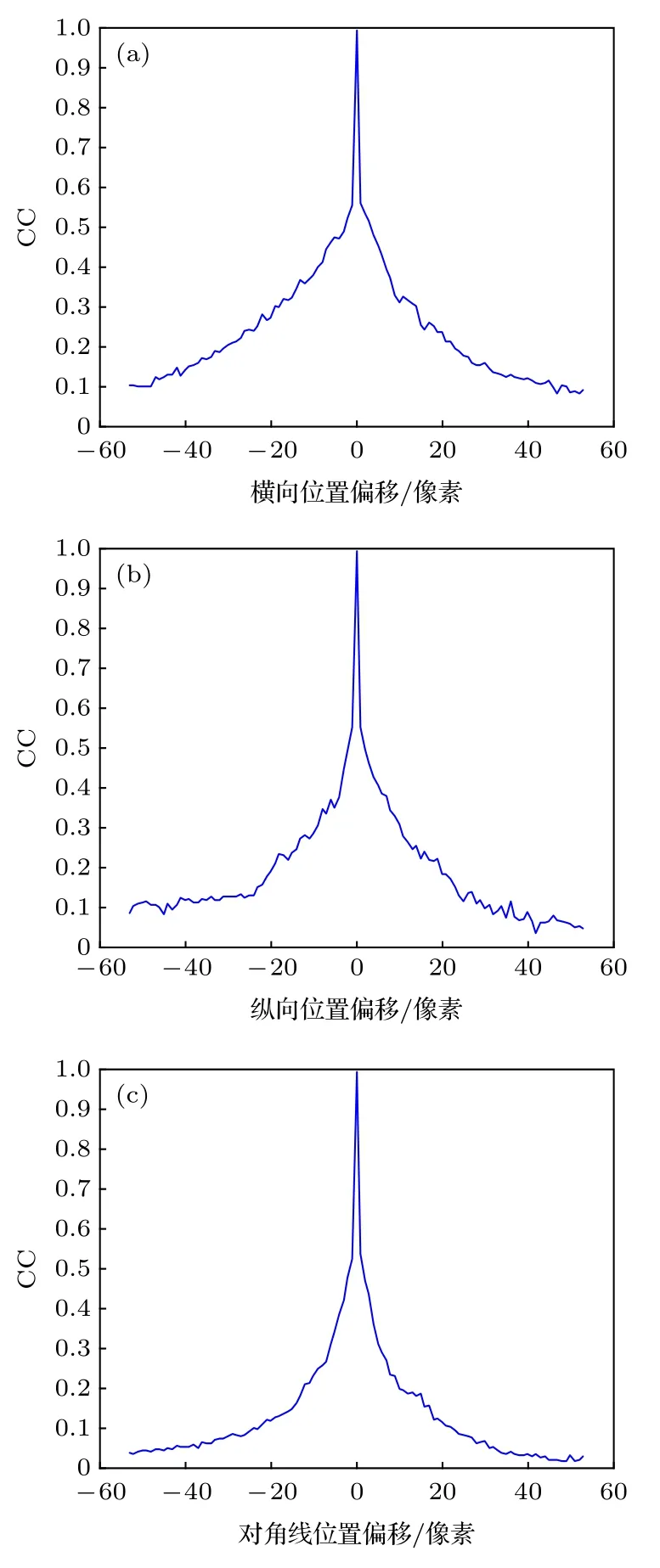
图 10 图像剪切位置的偏差对解密图像的影响Fig. 10. The effect of the deviation of the image cut position on the decrypted image.

从图8和图9中可以看出, 在解密错误时, 如果剪切图像尺寸小于正确尺寸, 解密效果更好一些, 这是因为此时的衍射系统加密图像φdif(x,y) 中,除去中心位置150 × 150部分, 剩下的65.7%的部分是正确的, 而且此时认为K2(x,y) 是正确的, 所以从图8中可以看出, 此时未被选择的信息Odif(x,y)依然可以还原出轮廓. 随着剪切图像的尺寸越来越大, 超过了正确解密尺寸, 衍射系统加密图像中的正确信息越来越少, 所以解密效果越来越差. 在这个过程中, 只要剪切图像尺寸错误, 选择性加密部分O4f(x,y) 始终是无法正确解密的, 因为如果剪切图像尺寸错误, 不仅无法正确剪切出φ4f(x,y) , 而且还无法得到正确的所以无法正确恢复出选择性加密信息O4f(x,y) . 而且, 当剪切图像尺寸为 149 × 149 和 151 × 151 时, 对应的 CC 分别为0.3021和0.2449, 这说明系统对选择性加密图像的尺寸敏感性极高.

如果攻击者已知图像剪切的尺寸, 图像剪切位置正确与否也会对明文的恢复造成影响, 图10展示了图像剪切位置的偏差对解密图像的影响.

从图10中可以看到, 在解密过程中, 当图像剪切的位置在横、纵方向上偏差 ±6个像素以上,CC小于0.4; 当图像剪切的位置在对角线方向上偏差 ±3 个像素以上, CC 小于 0.4; 当 CC 小于0.4时, 解密图像与原始图像低相关, 解密效果很差. 图10说明了系统对选择性加密图像的位置也很敏感.

3.2.3 系统对衍射距离和波长的敏感性分析

对于衍射加密系统来说, 衍射距离和波长是可以作为密钥的, 此前已经有很多针对衍射加密系统的研究[9,24], 这些研究都证明了衍射加密系统对于衍射距离和波长的敏感性. 本节只对系统中的衍射系统部分进行分析, 结果如图11所示. 本文提出的系统中, 两次衍射距离都是透镜的焦距的2倍,在实际的应用中, 两次衍射距离完全可以不同, 可以为任意距离.

3.3 系统的抗衍射攻击能力分析

本文还分析了系统的抗衍射攻击能力, 在本节的分析中, 假定攻击者已经破获正确密钥K2(x,y) 、衍射距离和衍射波长, 对加密图像直接通过两次菲涅耳衍射进行解密, 过程示意图如图12所示, 其中O′(x,y) 表示通过攻击得到的解密图像, 结果如图13所示.

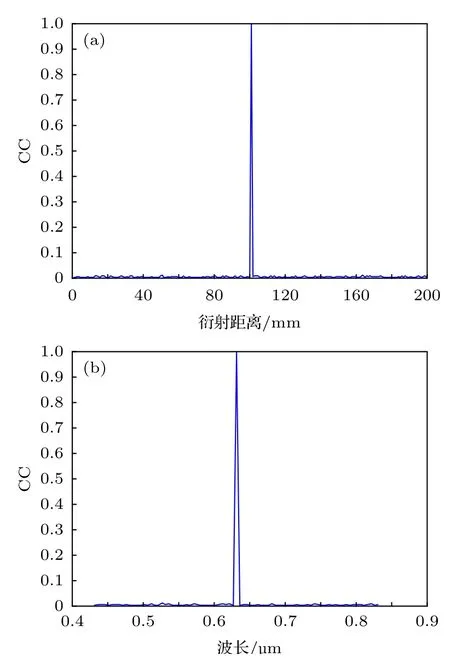
图 11 解密时衍射距离和波长对解密图像的影响, 正确的衍射距离为100 mm(两次衍射距离相同), 正确的波长为0.632 µm (a)衍射距离对解密图像的影响; (b)波长对解密图像的影响Fig. 11. The effect of diffraction distance and wavelength on decrypted image during decryption: (a) The effect of diffraction distance on the decrypted image; (b) the effect of wavelength on decrypted image. The correct diffraction distance is 100 mm (the two diffraction distances are the same), and the correct wavelength is 0.632 µm.

图 12 衍射攻击过程示意图Fig. 12. Schematic diagram of diffraction attack process.

图 13 衍射攻击得到的解密图像, CC = 0.2841Fig. 13. Decrypted image obtained by diffraction attack,CC = 0.2841.

从图13可以看到, 即使攻击者破获了正确的密钥K2(x,y) , 对于本文提出的系统中的选择性加密区域依然无法有效破解, 所以被选择性加密的明文O4f(x,y) 相对于未被选择性加密的明文Odif(x,y)来讲更为安全. 因此在加密过程中, 加密者可以将原始图像中更为重要的信息设置为O4f(x,y) , 以此来提高重要信息的安全性.

3.4 系统的鲁棒性分析

3.4.1 系统对噪声的鲁棒性分析

本节利用不同方差的高斯噪声作为噪声源, 对加密图像进行叠加干扰, 对比了本文提出的系统与基于4f系统的DRPE系统和基于菲涅耳衍射的DRPE系统的抗噪性, 仿真结果如图14所示, 所加的高斯噪声大小为加密图像的均值大小乘以s,其中s为高斯噪声的方差. 由图14可以看到, 虽然本文提出的系统对噪声的鲁棒性不如另外两种系统, 但是当高斯噪声方差小于0.1时, 解密图像和原始图像之间的CC值保持在0.4之上, 可以认为, 本文提出的系统具有良好的抗噪声干扰能力.

图 14 不同的系统对高斯噪声的鲁棒性Fig. 14. Different system robustness to Gaussian noise.

3.4.2 系统对加密图像数据丢失的鲁棒性分析

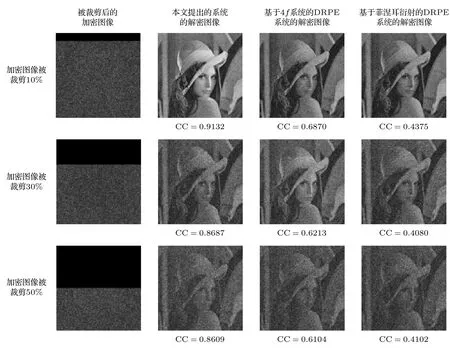
图 15 加密图像被裁剪不同比例时不同系统得到的解密图像Fig. 15. Decrypted images obtained by different systems when the encrypted image is cropped at different ratios.

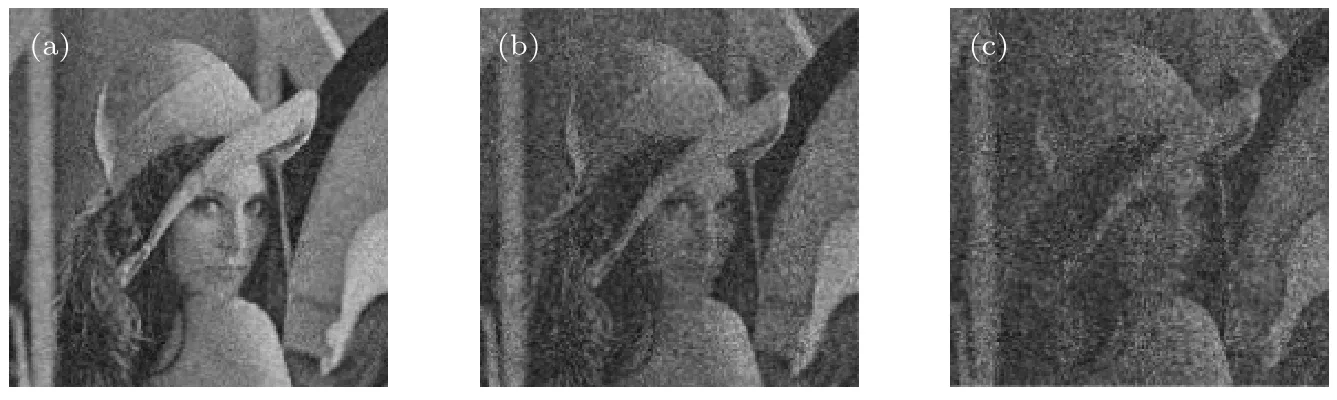
图 16 加密图像数据随机丢失的解密图像 (a)随机丢失 10%; (b)随机丢失 30%; (c)随机丢失 10%Fig. 16. Decrypted images where encrypted image data is randomly lost: (a) Randomly lost by 10%; (b) randomly lost by 30%;(c) randomly lost by 40%.

本节研究了加密图像对数据丢失的鲁棒性, 系统的抗裁剪性仿真实验结果如图15所示. 当加密图像被裁剪10%时, 对原始图像复原影响不大, 因为此时只丢失了小部分衍射加密图像, 从解密图像中也能看出此时只有衍射部分受到了影响; 当加密图像被裁剪30%时, 此时不仅丢失了衍射加密图像, 4f系统的加密图像数据也丢失了一部分, 所以从解密图像上来看, 图像整体都受到了影响, 但依然可以识别出图像的主要信息; 当加密图像被裁剪50%时, 解密图像与原始图像之间的CC值依然保持在0.4以上, 依然可以识别出图像的轮廓信息. 对比本文提出的系统与基于4f系统的DRPE系统和基于菲涅耳衍射的DRPE系统的抗裁剪性,本文提出的系统的抗裁剪性较优于另外两种系统,可以认为, 本文提出的系统具有较好的抗裁剪性.

另外, 本节还研究了当加密图像数据随机丢失时, 解密图像的恢复情况, 结果如图 16所示, 其中(a), (b), (c)分别为加密图像数据随机丢失10%,30%, 50%时的解密图像, 它们与原始图像的CC 值分别为 0.8616, 0.6315, 0.4273, 均大于 0.4,可以认为, 本文提出的系统对于数据丢失具有较好的抗干扰能力.

4 结 论

本文提出了一种基于双随机相位编码的局部混合光学加密系统. 该系统采用共孔径、双光路的光学设计结构, 将4f系统与衍射系统相结合, 实现了对图像中局部信息的选择性加密. 将4f系统作为选择性加密通道, 原始图像中的局部信息通过选择性分光进入4f系统中加密, 将得到的选择性加密图像替换到经过衍射系统得到的加密图像中, 完成最终的局部混合加密. 通过统计特性分析等, 证明了该系统的有效性. 同时, 分析了系统的密钥敏感性, 证明了系统对选择性加密图像的尺寸大小和位置的敏感性极强, 结合系统受到衍射攻击时的结果, 证明了该系统可以有效对重要信息进行更加安全的选择性加密. 与传统光学加密系统相比, 该系统可以在保证非重要信息的安全性的同时, 提高原始图像中重要信息的安全性; 与目前现有的选择性加密方案相比, 该系统易于通过光学方法实现, 具有较高的应用价值.