基于DDPG算法的无人机集群追击任务
2020-11-06张耀中许佳林姚康佳刘洁凌
张耀中,许佳林,姚康佳,刘洁凌
1.西北工业大学 电子信息学院,西安 710072 2.西安北方光电科技防务有限公司,西安 710043
无人机与有人飞机相比,具有体积小、造价低、使用方便、对作战环境要求低、战场生存能力强等优点。在过去的几十年里,伴随着导航、传感器、能量存储与制造等相关技术的发展,无人机在军用和民用领域都得到了广泛的应用。
随着无人机在相关领域应用的不断推进,单架无人机在执行任务时暴露出了灵活性差和任务完成率低的短板,因此使用多架无人机构成集群协同执行相关任务必将成为无人机未来应用的重要发展方向。无人机集群可以看作是一个多Agent 系统(Multi-Agent Systems,MAS),其目标是协调集群内的无人机实现一个共同的任务目标。
当前对无人机集群的众多研究都集中在协同任务决策方面,通过蚁群算法、狼群算法等有关的群体智能算法来实现对多架无人机的指挥控制。但这些方法有着计算时间过长、灵活性不足、智能化程度低的缺点,无法很好地满足无人机集群对于无中心化、自主化、自治化的要求。相比而言,人工智能领域中的深度强化学习方法凭借着其强大的高维度信息感知、理解以及非线性处理能力,有望使无人机集群在面向战场复杂任务时有足够的智能协同完成作战任务。
目前,已经有诸多学者使用深度强化学习方法对无人机集群的相关问题进行了探索性研究。其中,Pham等基于深度强化学习算法对无人机的自主导航过程进行了研究,并应用于自主目标区域覆盖问题,在一定程度上解决了无人机集群联合行动下的协同任务规划问题和高维度状态空间的挑战[1-2];Qi和Zhu使用深度强化学习研究了智能体的环境感知问题,实现了对相邻智能体的意图感知[3];李高垒[4]和魏航[5]使用深度强化学习方法研究了影响无人机自主空战的相关因素,为未来智能空战提供了理论依据。Yamaguchi引入反馈控制律研究多机器人的协调运动问题,采用队形矢量法控制机器人群体队形实现了对目标的追击[6]。目前已有部分学者采用人工智能算法来解决无人机对目标的追击问题,如Gadre采用Q学习算法在栅格化环境下研究了智能体的追击问题,并与动态规划算法进行对比,取得了较好的效果[7]。苏治宝等通过对未知环境中多移动智能体追击单目标问题的研究,采用强化学习中的Q学习算法给出了相应的解决方案[8]。通过对相关文献的分析可以看出,目前在无人机集群应用方面的研究还不够完善,所研究问题的规模都比较小,而且大多采用栅格化的任务环境,导致应用环境过于简单。
与此同时,一些军事强国,如美、英、俄罗斯等都在开展将人工智能技术应用于无人机集群任务的相关实验验证,美国已经开展了多个智能化无人机集群项目,2016年美军在加州进行的无人机集群实验,成功地将人工智能技术应用到无人机集群的行为决策中,实现了无人机集群在空中自主协作,组成无人机集群队形,并完成预定任务,充分体现了无人机集群的无中心化、自主化、自治化,这一实验表明美军在无人机集群自组网以及任务决策方面已经达到了实用化水平[9]。因此,进行无人机集群的应用研究具有一定的理论意义和使用价值。
本文在现有研究的基础上,以无人机集群对敌方来袭目标的追击任务为场景[10],基于深度确定性策略梯度网络(Deep Deterministic Policy Gradient,DDPG)算法建立了人工神经网络模型,设计了一种引导型回报函数有效解决了深度强化学习在长周期任务下的稀疏回报问题,通过引入基于滑动平均值的软更新策略减少了DDPG算法中Eval网络和Target网络在训练过程中的参数震荡,提高了算法的训练效率。仿真实验结果表明,训练完成后的无人机集群能够较好地执行对敌方来袭目标的追击任务,表现了人工智能算法在提升无人机集群指挥决策能力上的应用潜力。
1 任务场景描述
如图1所示,在任务场景中出现敌方目标,目标的初始位置已知,保持高度和速度恒定飞行,我方派出无人机集群进行追击拦截。设定双方都处于同一个水平面内,不考虑高度因素。不同于以往将任务环境网格化的离散处理方案,本文构建了连续的二维战场地图作为无人机集群追击问题的任务环境,集群中的无人机、被追击目标的位置,均采用连续的空间位置坐标表示。

图1 无人机集群执行追击任务示意图Fig.1 Schematic diagram of UAV swarm for pursuit task
本文针对任务场景中只有一个目标出现的情况,且不考虑目标针对无人机集群进行机动规避等行为,目标按照自身预定的运动策略进行飞行。无人机集群的任务是围堵目标,实现对目标的打击或者驱离,当无人机集群与目标之间的距离满足一定的态势要求后,视为无人机集群完成追击任务[11-12]。
2 无人机集群模型
2.1 无人机运动控制模型
为了便于问题分析,将集群中的无人机看作质点运动模型,使用两个方向的加速度来控制无人机的运动过程,如图2所示。

图2 无人机的运动学模型Fig.2 Kinematic model of UAV
无人机的质点运动方程表示为
(1)
(2)
(3)

针对式(1)~式(3)建立的无人机运动控制模型,为了便于强化学习算法的实现,采用2个方向的加速度作为控制量对无人机的运动行为进行控制,如图3所示。
由图3可知,无人机的行为空间包含切向加速度a∥和法向加速度a⊥2个维度,无人机的行为即深度强化学习算法的输出可以是这2个维度中满足范围要求的任意值,限定无人机的行为空间满足:
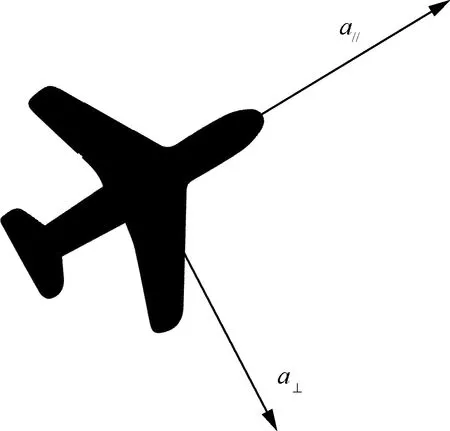
图3 无人机加速度控制模型图Fig.3 Diagram of UAV acceleration control model
(4)
同时,对无人机的速度做出限制,规定无人机的速度v∈[3,7] m/s。
2.2 无人机传感器探测模型
设定集群中的无人机具有对任务场景的全局探测能力,为了模拟传感器的真实探测效果,对无人机的传感器探测结果加入一个服从正态分布ε~N(μ,σ2)的随机误差。误差的参数为
(5)
式中:di_t为无人机到目标的距离。
因此,集群中每架无人机对目标位置的探测结果为
(6)
式中:(xg,yg)为无人机探测到的目标位置;(x′g,y′g) 为目标的真实位置;εx、εy为服从正态分布N(0,σ2)的随机误差。
无人机对目标速度的探测结果计算为
(7)
式中:(xg_old,yg_old)为上一时刻探测到的目标位置;(xg_now,yg_now)为当前时刻探测到的目标位置。
2.3 集群内无人机信息交互模型
集群内的无人机之间需要进行信息交互以便使无人机集群具有更好的协作行为决策,每架无人机都有固定的通信范围,在通信范围内的无人机之间可以进行通信,为了便于仿真分析,设定每架无人机最多可以与通信范围内距离最近的3架无人机进行信息交互,如图4所示。
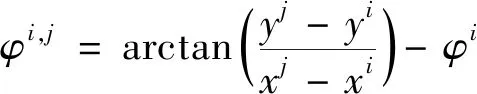
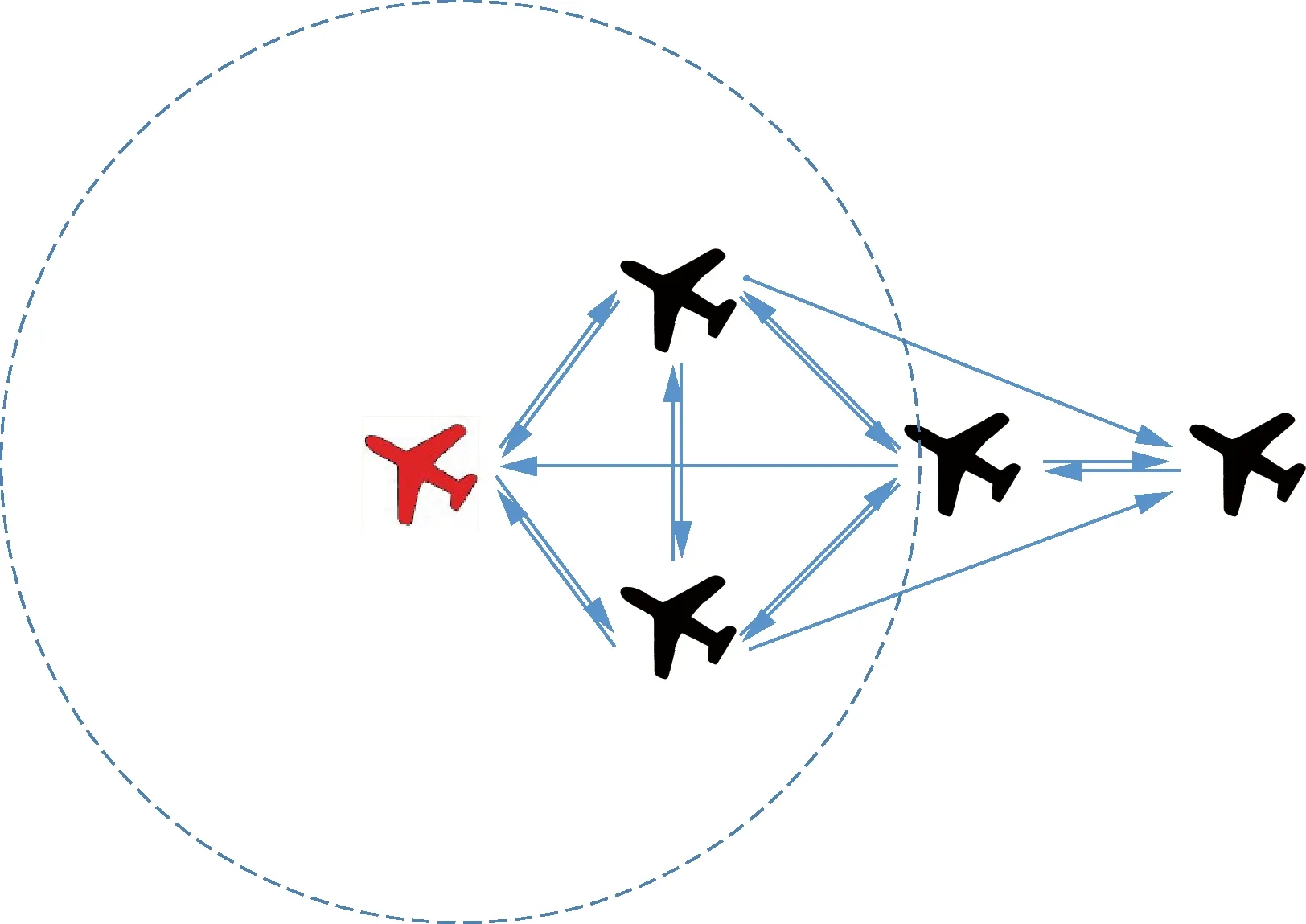
图4 集群内信息交互关系示意图Fig.4 Schematic diagram of interaction within swarm

图5 无人机间态势信息关系图Fig.5 Situational relationship between UAVs
3 深度确定性策略梯度网络算法
DDPG算法是一种结合了基于值迭代和策略迭代的深度强化学习算法[13-14]。该算法的优势在于可以针对无限大小的状态空间和行为空间实现智能体对最优策略的学习,使无人机集群在针对具体任务的学习过程中具有更优良的性能表现。DDPG算法是在传统的“演员-评论家”算法的基础上改进形成的,下面对算法网络的结构进行详细分析。
3.1 “演员-评论家”算法
“演员-评论家”算法主要由2个不同的网络模块组成,分别是演员网络模块和评论家网络模块。
演员网络模块主要通过对输入环境的状态观测,利用人工神经网络得到智能体行为的选择概率,完成智能体与环境的交互过程,并且用交互得到的环境回报对人工神经网络的参数进行更新,用来维护和更新智能体的动作选取策略。
评论家网络模块则通过对输入环境的状态及行为进行观测,来评估每个环境状态与行为的价值,即估计演员网络模块的价值,通过实际网络价值与预测网络价值的误差来更新当前神经网络。评论家网络模块输出的价值可以对演员网络模块的行为选取策略进行指导,这也是“演员-评论家”算法的由来。
由上述可知,对于“演员-评论家”算法2个不同的网络模块:演员网络模块和评论家网络模块分别需要建立各自的人工神经网络。演员网络模块的人工神经网络实现了从观测状态到智能体行为选取概率的映射,其训练过程需要结合评论家网络模块的误差进行。而评论家网络模块的人工神经网络是通过对环境状态和行为选取的观测得到相应的评分,形成环境状态与行为到对应评分的映射。“演员-评论家”算法的模型结构如图6所示。
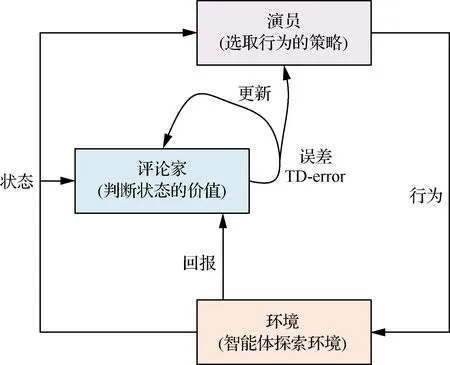
图6 “演员-评论家”算法的模型结构Fig.6 Model structure of “Actor-Critics” algorithm
3.2 DDPG算法的网络架构
DDPG算法融合了“演员-评论家”算法和深度Q网络算法,是一种新型的深度强化学习算法[15-16],算法的网络架构如图7所示。
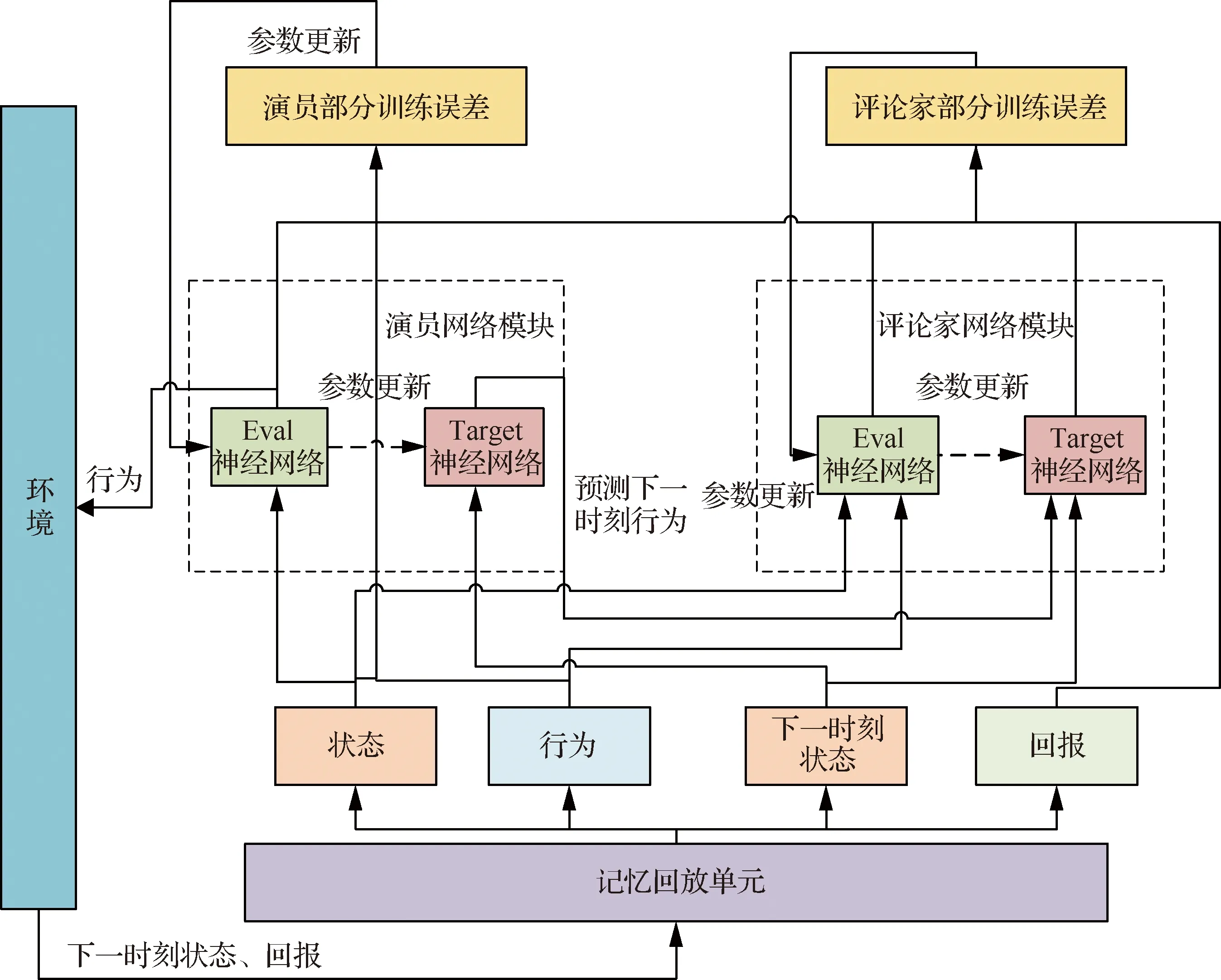
图7 DDPG算法的网络架构图Fig.7 Network architecture of DDPG algorithm
如图7所示,DDPG算法主要由环境、记忆回放单元、演员网络模块和评论家网络模块构成。其中,环境是智能体的交互空间,也是智能体的探索空间,智能体在与环境的交互过程中得到交互样本,并将交互样本存储到记忆回放单元中用于智能体的训练过程。为了优化算法的学习过程,DDPG算法吸取了深度Q网络算法的思想,对于算法中的网络部分分别构建了一对结构完全相同的人工神经网络,分别称为Eval神经网络和Target神经网络。其中Eval神经网络用于训练更新网络参数,Target神经网络则使用周期性软更新策略对Eval神经网络进行跟随,并协助Eval神经网络进行训练。
演员网络模块的神经网络用来完成对智能体行为选取概率的确定,智能体进行行为决策时,将依据演员网络模块提供的行为选择概率来选取行为与环境进行交互。评论家网络模块的神经网络通过接收环境状态和智能体行为,用来生成对“状态-行为”的价值评估。其中Eval神经网络用来判断当前状态与行为的价值,Target神经网络接收下一时刻的状态和演员部分Target神经网络输出的下一时刻行为,并进行价值判断。
DDPG算法中演员和评论家2部分的神经网络有着不同的功能和结构,相应的训练方式也不同,使用不同的损失函数进行训练。对于评论家网络而言,使用TD-error对Eval神经网络的参数进行训练,训练过程使用最小化损失函数Loss进行更新,即
TD-error=reward(st,at)+
(8)
Loss=(TD-error)2
(9)
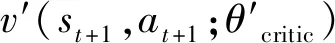
对于演员网络模块中神经网络的训练过程,通过最大化<状态,行为>相对应的价值判断来实现,因此使用对状态和行为的评价均值作为损失函数,即
Loss=-mean(v(s,a;θcritic))
(10)
3.3 DDPG算法中探索与经验的平衡
在DDPG算法中,如果只是依据算法输出的行为选择策略来决定无人机的当前行为,容易导致算法对任务环境探索的不充分,因此需要对DDPG算法策略增加一定的探索性[17]。根据DDPG算法的特点,增强算法探索性的实现方法是在无人机行为选取过程中增加一定的随机噪声[18-19],即
action=action′+Noise
(11)
式中:action为无人机当前时刻选择的行为;action′为DDPG算法中演员网络模块输出的无人机行为;Noise为随机噪声。
由于DDPG算法输出的是无人机在2个方向上加速度的连续控制量,因此采用上述方法增强DDPG算法的探索性具备良好的可行性,设定随机噪声服从正态分布:
Noise~N(μ,σ2)
(12)
噪声的期望值μ=0、方差σ与迭代轮次相关,随着网络训练迭代次数的增加σ将逐渐减小,为了保证无人机集群具备足够的探索能力,确保在无人机探索初期其行为选择能够选取到行为空间中的任意值,对随机噪声方差初始值的设计为
σ0=(actionmax-actionmin)/4
(13)
σ=Kepisodeσ0
(14)
式中:K=0.999 5;episode为算法训练代数。
3.4 DDPG算法的网络结构
由前述分析可知,DDPG算法由一对结构完全相同的神经网络,即“演员”部分人工神经网络(Actor网络)和“评论家”部分人工神经网络(Critic网络)构成[19-20],所构建网络的Tensorboard输出如图8所示。
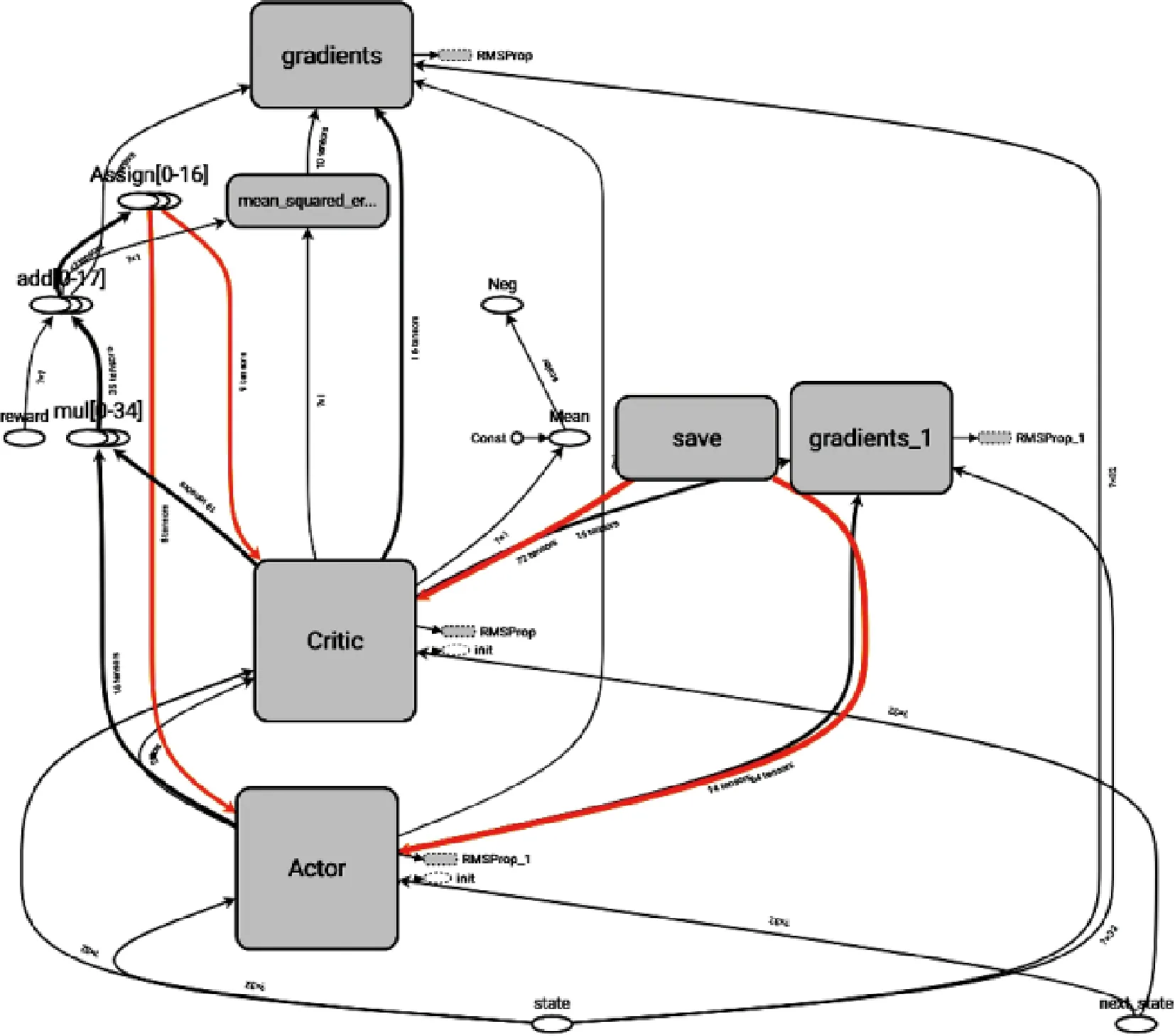
图8 DDPG算法网络结构(Tensorboard)Fig.8 Network structure of DDPG algorithm (Tensorboard)
3.4.1 “演员”网络模块的人工神经网络结构
“演员”网络模块的人工神经网络用来输出无人机的行为,在无人机集群追击任务环境中,无人机集群的状态空间为自身位置(xi,yi)、速度(vx_i,vy_i)、探测得到的目标位置(xg,yg)、速度(vx_g,vy_g)以及通过信息交互得到的其他无人机的相关信息(xij,yij)、(vx_ij,vy_ij)和其他无人机的探测信息(xij_get,yij_get)、(vx_ij_get,vy_ij_get),共32个维度作为无人机的状态空间,如图9所示。
对“演员”网络模块中的Target和Eval人工神经网络,构建了2个结构完全相同的6层全连接人工神经网络,每层网络的人工神经元个数分别为[100,100,300,100,100,2],最后一层神经网络为二维度的输出层,对应无人机的切向加速度a∥与法向加速度a⊥。输出神经元使用tanh(x)作为激活函数,实现网络输出与无人机行为的映射,其他各层的神经元使用relu(x)作为激活函数。并且使用RMSProp(Root Mean Square Prop)算法作为训练的优化器。“演员”网络模块中人工神经网络的结构如图10所示。图中“演员”
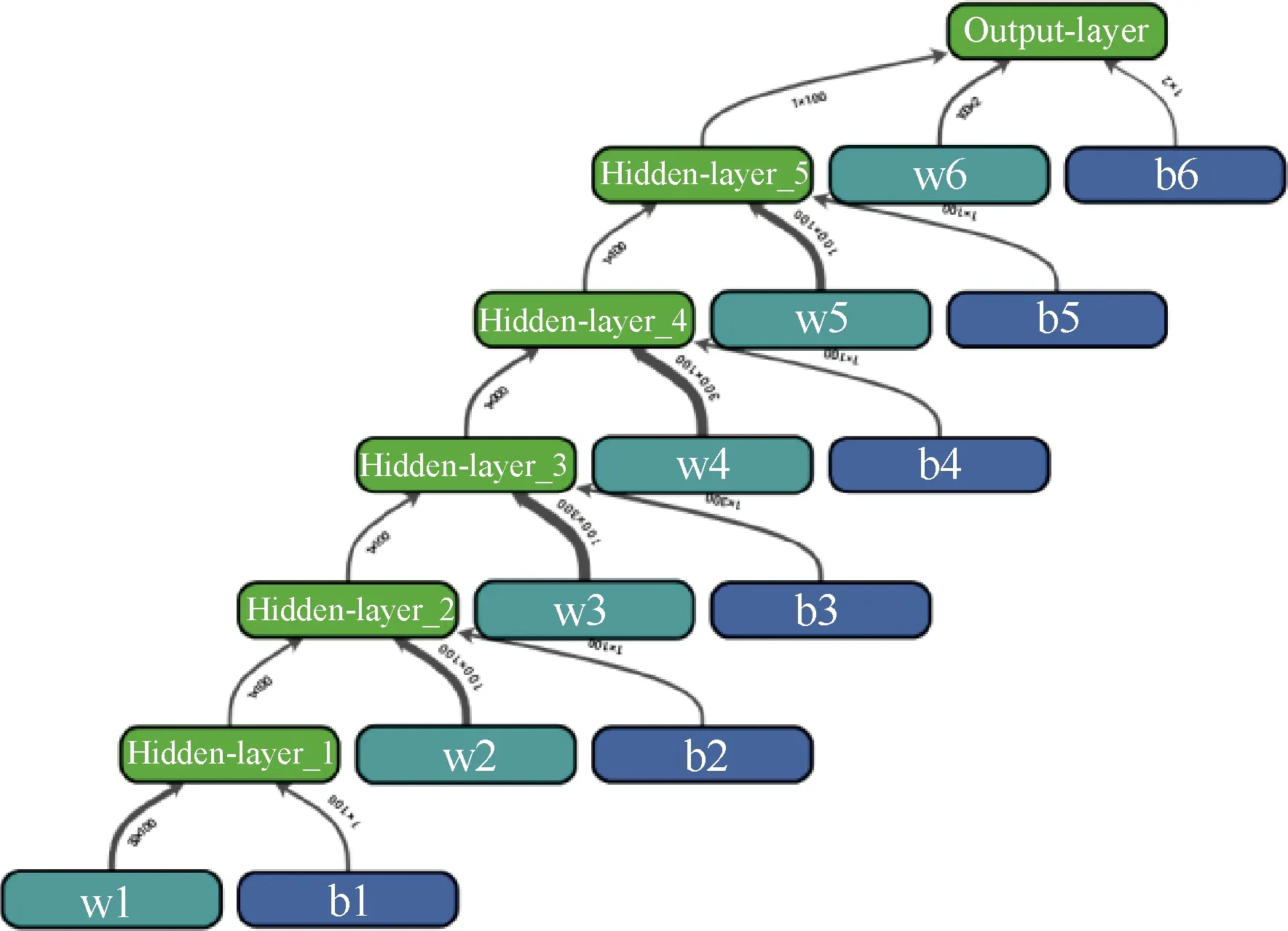
图10 “演员”网络模块中人工神经网络结构Fig.10 Network structure in “Actor” network module
网络模块中,w1,w2,…,w6和b1,b2,…,b6代表了6层网络中的权重值和偏置值。
3.4.2 “评论家”网络模块的人工神经网络结构
“评论家”网络模块的人工神经网络通过对“状态-行为”的价值评估,指导“演员”网络模块中神经网络的训练过程[21-23]。因此,评论家网络模块中神经网络的输入状态为无人机集群的状态信息与行为信息,网络的状态空间构成如图11所示。

图11 “评论家”网络模块的状态空间构成Fig.11 State space of “Critic” network module
对“评论家”网络模块中的Target和Eval人工神经网络,构建了2个结构完全相同的5层全连接人工神经网络,每层网络的人工神经元个数分别为[100,300,100,10,1]。输出层的神经元使用tanh (x)作为激活函数,隐藏层的神经元使用relu(x)作为激活函数,并且使用RMSProp(Root Mean Square Prop)算法作为训练的优化器。神经网络的结构如图12所示。

图12 “评论家”网络模块中的人工神经网络结构Fig.12 Network structure in “Critic” network module
在“演员”网络模块和“评论家”网络模块中同时存在Target和Eval人工神经网络,其中Eval神经网络用于训练过程,而Target神经网络则周期性的跟随训练网络相应参数的变化而更新。对于Target神经网络的参数更新使用基于滑动平均值的软更新策略,即
θTarget=kθTarget+(1-k)θEval
(15)
式中:θTarget为Target神经网络参数;θEval为Eval神经网络参数;k为滑动因子,经验取值为0.2。
3.5 DDPG算法的稀疏回报问题
对于连续的状态空间和行为空间,无人机进行随机初始化之后要经历一段很长时间与环境的交互过程才能达到最终状态。此时,仅在无人机集群到达最终状态之后给予相应回报的方式,有着回报周期过长的缺陷,容易导致强化学习过程无法进行有效学习,即存在着稀疏回报问题。
为了解决稀疏回报问题,对无人机集群的学习目标进行了相应的修改,增加有效回报,从而加快学习速度,构建不同情形下无人机的回报函数来指导深度强化学习的学习方向,即
(16)
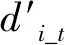

对于式(16)中的无人机集群回报函数,由无人机与目标之间的距离变化情况、无人机的速度方向以及无人机的速度大小共同表示。当无人机与目标之间的距离变小时对应的回报函数为正值;由无人机的速度大小与速度方向相结合构成了回报函数,在相同速度大小的情况下,速度矢量的方向越指向目标,无人机的回报就越高;同理,在无人机速度方向指向目标的情况下,无人机的速度越大回报越高;对于无人机速度方向远离目标的情况下,无人机的速度越大,其负向回报越高。
由于无人机集群从初始状态出发,需要运行较长时间才能到达目标状态,如果在长时间的中间状态下无法得到环境的有效回报,容易导致算法训练过程中的梯度消失,从而导致训练过程无法收敛。无人机集群采用上述引导型回报函数时,训练过程中会根据无人机的任一状态产生一个与当前<状态,行为>相对应的价值回报,从而引导无人机集群逐渐向目标状态转移。因此,式(16) 能较准确地反应无人机的行为收益,算法的训练结果表明,通过采用引导型回报函数能够较好地解决深度强化学习中的稀疏回报问题。
3.6 DDPG算法程序流程
使用DDPG算法对无人机集群的追击任务进行训练,程序实现流程如图13所示。

图13 DDPG算法的程序流程图Fig.13 Algorithm flow chart of DDPG algorithm
4 仿真实验
设定仿真场景中只存在一个匀速前进的目标,当集群中的任意一架无人机追击到目标之后,视为无人机集群完成了对目标的追击任务,即到达了任务的最终状态。
4.1 训练过程
仿真中使用5架完全相同的无人机构成集群进行训练。为了便于观察算法的训练状态,防止训练过程中出现梯度消失等现象,对人工神经网络的收敛性能进行了监测,分别选取“演员”和“评论家”网络模块中的神经网络参数进行统计观察,得到相关统计信息如图14~图17所示。
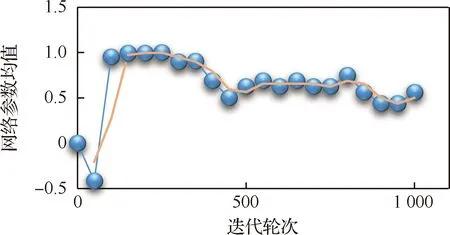
图14 “演员”网络模型Eval网络参数均值变化曲线Fig.14 Curve of average change in Eval network parameters in “Actor” network module

图15 “演员”网络模块Target网络参数方差变化曲线Fig.15 Curve of variance in Target network parameters in “Actor” network module

图16 “评论家”网络模块Eval网络参数均值变化曲线Fig.16 Curve of average change in Eval network parameters in “Critic” network module
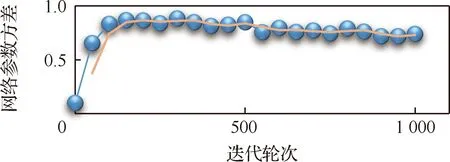
图17 “评论家”网络模块Target网络参数方差变化曲线Fig.17 Curve of variance in Target network parameters in “Critic” network module
图14~图17数据曲线图分别是对“演员”和“评论家”网络模块中的神经网络参数取均值和方差进行统计的结果,图中实线为网络参数统计的真实值,虚线则是对统计数据进行周期为3的滑动平均处理的结果,用来表明参数统计的变化趋势。由上述参数统计曲线图可以看出人工神经网络在训练过程中很好地实现了收敛。
图18截取自TensorBoard的“评论家”网络模块中的神经网络参数分布变化直方图,由远及近(颜色由深变浅)表现了神经网络在不同训练阶段各个神经元参数分布的变化情况,横向表示神经元各个参数取值,从神经网络的参数统计变化曲线图与参数分布变化直方图可以看出,人工神经网络的参数分布情况在训练过程中逐渐收敛到稳定的分布状态。
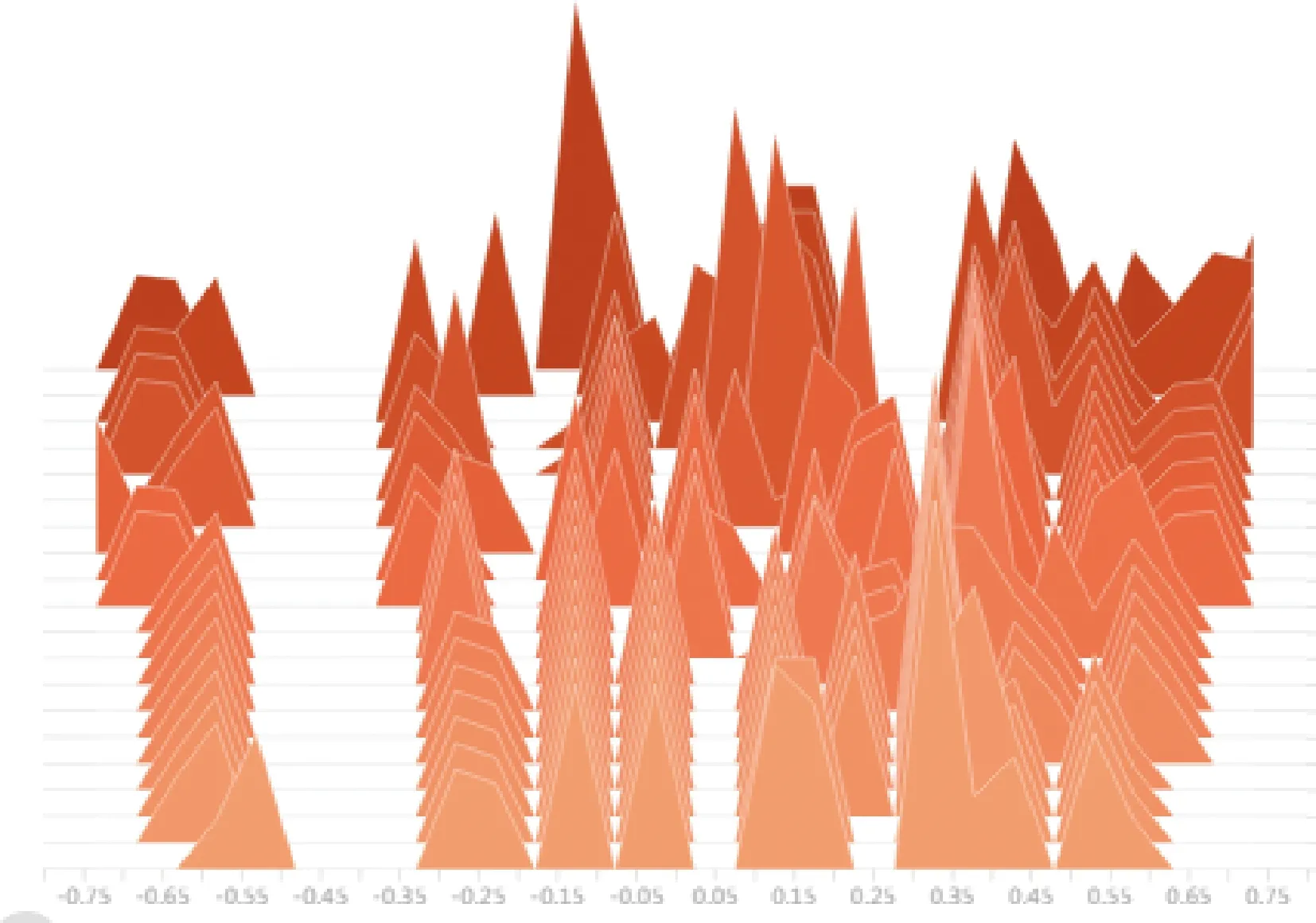
图18 “评论家”网络模块Eval网络参数分布变化曲线Fig.18 Eval network parameter distribution curves in “Critic” network module
无人机集群在不同训练轮次下的平均回报值变化趋势如图19所示。
由图19可见,在算法的训练过程中,无人机集群的行为收益值保持比较平稳的状态缓慢增加,说明无人机集群行为随着训练过程的不断进行有着越来越好的表现。

图19 无人机集群在不同训练轮次下的平均回报值Fig.19 Mean value of rewards under different training epochs for UAV swarm
随着算法训练回合的增加,无人机集群在环境中的回合总回报变化趋势如图20所示。

图20 无人机集群在不同迭代轮次下的回合总回报Fig.20 Total rewards under different training epochs for UAV swarm
无人机集群在不同训练轮次下的任务完成率如图21所示。
从图21可以看出,完成训练后无人机集群执行对敌来袭目标追击任务的成功率可以达到95%左右。

图21 无人机集群在不同迭代轮次下的任务成功率Fig.21 Task completion rate under different training epochs for UAV swarm
4.2 验证过程
使用5架相同无人机构成集群完成所创建神经网络的训练后,对训练完成的模型进行了测试验证。使用训练完成的无人机集群执行对目标的追击任务,生成5架无人机集群及目标的初始状态,得到无人机集群追击任务的轨迹图如图22所示。
如图22所示,使用训练完成的神经网络模型很好地实现了5架无人机构成集群执行对目标的追击任务。为了验证模型对于动态数量无人机集群的适用性,分别使用10架和20架无人机构成集群,对无人机集群的追击任务进行验证,得到无人机集群轨迹图如图23和图24所示。

图23 10架无人机执行追击任务的轨迹Fig.23 Trajectory of 10 UAVs on pursuit mission

图24 20架无人机执行追击任务的轨迹Fig.24 Trajectories of 20 UAVs on pursuit mission
由图22~图24可以看出,基于5架无人机训练得到的模型能很好地应用于10和20架无人机用来执行对敌来袭目标的追击任务中,可以看出,DDPG算法对无人机集群的行为决策有着良好的适应能力和泛化能力。
为了进一步验证本文基于改进DDPG算法无人机集群模型的泛化能力和适应能力,对具有不同程度的逃逸策略的机动目标使用训练完成的集群模型进行了实验验证,得到无人机集群轨迹图如图25所示。由图25仿真结果可以看出,对于具有简单逃逸策略的来袭目标,无人机集群很好地完成了预定的追击任务。

图25 简单逃逸策略下对20架无人机的追击任务轨迹Fig.25 Trajectories of 20 UAVs on pursuit mission with simple escape strategy target
在图26的追击任务场景中,当目标采用大机动逃逸运动策略时,由于来袭目标快速逃逸出了设定的任务边界导致目标逃逸成功,但是训练完成后的无人机集群仍然很好地完成了对预定目标的追击任务。

图26 大机动逃逸策略下对20架无人机的追击任务轨迹Fig.26 Trajectories of 20 UAVs on pursuit mission with big maneuver escape strategy target
仿真实验表明,深度强化学习能够很好地满足了无人机集群对于无中心化、自主化和自治化的要求。将人工智能算法应用在无人机集群的任务决策中具有很好的发展前景。
5 结 论
本文基于深度强化学习中的DDPG算法对无人机集群追击任务进行了研究,为了平衡DDPG算法“探索-经验”的矛盾,在训练过程中对无人机行为加入了自适应的噪声单元,以增强算法的探索能力。为了提升算法性能,引入基于滑动平均值的软更新策略减少了DDPG算法中Eval神经网络和Target神经网络在训练过程中的参数震荡,提高了算法的收敛速度。为解决深度强化学习中的“稀疏回报”问题,设计了指导型回报函数,避免了无人机集群在长周期训练条件下无法有效学习的问题,提升了算法的收敛性。
训练完成后的无人机集群能够很好地执行追击任务。同时验证了在不改变网络模型和状态空间结构的前提下,训练完成的模型能直接应用于更多无人机构成的集群追击任务中和具有不同程度逃逸策略的机动目标追击任务中。仿真结果表明使用DDPG算法针对无人机集群的追击任务可以求解出良好的行为策略,体现了基于人工神经网络的强化学习算法在提升无人机集群指挥决策模型的泛化能力上的巨大应用潜力。
