基于微型涡喷发动机热喷流的无源流体推力矢量喷管的控制规律
2020-11-06龚东升顾蕴松周宇航史楠星
龚东升,顾蕴松,周宇航,史楠星
南京航空航天大学 航空学院 非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016
推力矢量控制(Thrust Vector Control,TVC)指推进系统除了为飞行器提供前飞推力外,还能同时或单独地为飞行器俯仰、偏航、滚转方向提供控制力及力矩,用于全部或部分取代飞行器舵面进行飞行姿态控制[1]。推力矢量技术是未来先进飞行器的关键技术之一[2],它的应用能够显著增强飞行器的隐身性,提高机动性[3]、敏捷性和空中格斗能力,实现短距起降[4]。
推力矢量主要分为机械式和流体式两类。目前机械式推力矢量技术已应用于型号,例如美国的F-22和俄罗斯的Su-35。机械式通过转动尾部喷管直接改变射流方向达到推力矢量效果,控制原理相对简单、控制规律线性、易实用化,但它存在“结构重量重、活动部件多、偏转机构复杂、射流偏转响应慢”等不足。而流体式推力矢量控制(Fluid Thrust Vector Control,FTVC)基于流动控制原理实现射流偏转,克服了机械式诸多不足,具有“喷管型面固定、活动部件少、结构重量轻、射流偏转响应快”等显著优势,成为推力矢量技术的重要研究方向,具有重要的工程实用价值和应用前景[5]。1982年,麦道航空航天公司的Haloulakos[6]首次将该类控制方式定义为“流体推力矢量控制”。流体推力矢量又可分为有源流体式和无源流体式,有源流体推力矢量控制的实现形式主要有激波矢量控制、喉道偏斜控制、双喉道控制、逆向流控制、同向流控制。随后十几年里美国空军技术学院对上述流体推力矢量技术的偏转机制和性能进行了研究,发现其射流偏转双稳态(矢量角二值化)、矢量角脉动不稳定等问题突出[7]。
1972年,美国Rohr公司联合NASA兰利研究中心首次提出基于Coanda壁面吹气的控制方法[8],这是同向流控制的雏形。20世纪90年代初,美国明尼苏达大学Strykowski和Niccum[9]首次提出了“逆向流”概念并论证了技术可行性。NASA兰利研究中心的Chiarelli[10]、北京航空航天大学的王强[11]等对激波矢量控制进行了大量研究;NASA兰利研究中心的Wing[12]、洛克希德·马丁公司的Catt[13]、南京航空航天大学的范志鹏[14]、顾瑞[15]、谭慧俊[16]等对喉道偏斜及双喉道控制进行了大量研究。2004年南京航空航天大学的李念等[17]对自耦合射流控制主射流的矢量偏转进行了实验研究,利用自耦合射流在出口截面附近对主射流强烈的卷吸作用,使主射流产生了显著的矢量偏转。2013年韩国航空大学的Song等[18]利用有源二次射流和Coanda效应实现了超声速主射流的推力矢量控制。2017年,印度理工学院坎普尔分校的Sekar等[19]利用横向射流和主射流相互作用实现了流体推力矢量三元矢量控制。研究表明,利用二次流和主射流相互作用能够实现主射流矢量偏转。
发展至今,人们对有源流体推力矢量技术已经进行了大量的研究,并且在无人验证机如英国的“恶魔”上进行了试飞验证[20-21],如图1所示。

图1 英国 “恶魔”无人机[20-21]Fig.1 “ Demon” unmanned aerial vehicle in the United Kingdom[20-21]
但其依然存在“外接气源、管路和控制规律复杂、能耗大”等不足[22-23]。因此无源流体推力矢量技术研究逐渐得到了各国的重视,该技术无需外接气源,射流矢量偏转响应快,矢量偏角大,能耗小,符合未来先进飞行器的发展需求。
无源流体推力矢量采用的是被动控制手段,不需要任何的二次流能量输入,相比于其他流体推力矢量技术具有自己独特的优势。
南京航空航天大学徐惊雷带领的驭风团队对无源双喉道气动矢量喷管进行了大量的研究,2013年顾瑞[24]在常规双喉道气动矢量喷管的基础上,进一步研究提出了一种新型双喉道气动矢量喷管,在喷管内部增加新的次流流道,使喷管自身的部分气流相互作用,喷管在产生有效推力矢量角的同时,不需要从发动机引气,保证了喷管整体的工作性能,喷管构型如图2所示。林泳辰等[25]在2019年利用无源双喉道气动矢量喷管完成了无舵面飞翼的飞行试验。如图3(a)采用两个旁路式双喉道气动推力矢量喷管各自沿X轴左、右滚转45°安装,组成单发动机倒Ⅴ形布置的喷管,飞行器如图3(b)所示。

图2 新型双喉道气动矢量喷管示意图[24]Fig.2 Schematic diagram of a new type of double throat fluid vector nozzle[24]
2012年南京航空航天大学曹永飞[26]和中国空气动力发展与研究中心肖中云等[27]分别对一种基于Coanda效应的新型矢量喷管开展了实验和计算研究,该方法利用主射流的卷吸引射作用,二次流直接从外界大气中获取,称为“被动二次流”,主要目的是降低二次流能量消耗。该方法实现射流偏角在0°~13°范围内变化,但当偏角大于13°以后,主射流发生附壁现象,导致偏角突然增大,出现明显的射流偏转突跳问题。
2015年曹永飞等[28]采用被动二次流和Coanda壁面相结合的方式对低速主射流进行矢量偏转控制。如图4所示,其采用两段式Coanda壁面,即在喷管出口下游有12°和24°两次扩张,采用改变控制缝入口面积的方法实现了主射流的可控偏转。研究结果表明被动二次流控制方式是一种高效的射流矢量偏转控制手段,主射流两侧的压力差是造成其偏转的直接原因。

图4 二元流体式推力矢量喷管模型示意图[28]Fig.4 Schematic diagram of two-dimensional fluid thrust vector nozzle model[28]
2018年南京航空航天大学韩杰星[29]对控制缝的形式对矢量性能的影响进行了相关研究。采用了如图5(a)所示的流体推力矢量喷管,其中将二次流控制缝改为连续排列的圆孔形式后对喷管进行测力研究,研究结果表明该喷管也存在力矢量角控制不连续现象,如图5(b),其中横坐标为二次流控制阀门闭合度δ,纵坐标为推力矢量角α,本文定义射流上偏矢量角为正,下偏矢量角为负。

图5 无源流体推力喷管控制规律研究[29]Fig.5 Study on control law of passive fluid thrust nozzle[29]
由于国内外对基于Coanda效应的无源流体推力矢量技术的研究起步较晚,部分研究获得的控制规律存在矢量控制不连续、控制非线性等问题,且大量的研究都使用电动涵道风扇作为动力,其射流为常温、低速度射流,得到的控制规律不具有通用性、全面性。本文在文献[29]的基础上改进喷管设计,设计一种新构型的无源流体推力矢量喷管,喷管构型如图6所示。与文献[29]中的喷管相比,本文设计的喷管具有以下特点:

图6 喷管结构参数图Fig.6 Structural parameter diagram of nozzle
1) 都采用基于Coanda效应的无源流体推力矢量控制方式。利用射流引射作用产生低压区,喷管两侧形成的压差使射流方向偏转[27],利用Coanda附壁效应实现射流的稳定附壁,最终实现射流的稳定可控偏转。矢量控制无需额外二次流供气气源,喷管结构重量轻、活动部件少,控制结构简单。
2) 本文将喷管平直后缘改进为带V型夹角的后缘,设计夹角αe=90°,将每一侧的Coanda壁面一分为二,在射流方向Coanda壁面具有一定的后掠角,利用Coanda壁面的展向流动和三维效应,力求消除射流偏转的突跳问题。
3) 本文采用微型涡喷发动机取代以往使用的电动涵道作为动力,涡喷射流具有温度高、速度高的特点,模拟无人机飞行中喷管的实际工况,获得该喷管在涡喷发动机作为动力时推力矢量角控制规律,为后续无源流体推力矢量技术涡喷验证机的飞行提供数据支撑和理论依据。
1 实验模型及测试技术
1.1 实验模型及工作原理
设计的新型无源流体推力矢量喷管如图6所示,喷管由Coanda壁面、二次流流入孔、静压空腔和控制阀门4部分构成。喷管横截面为大宽高比的矩形截面,其中H1/H2=10∶1,出口V型夹角αe=90°,侧板长度L3=4.2H2,Coanda壁面沿流向偏转角αc=18°,壁面沿流向长度L4=2.25H2,在Coanda壁面靠近偏转角位置设置一排圆形二次流流入孔,单侧圆孔总面积S1=0.176S,其中S为涡喷发动机尾排气口面积。二次流控制阀门形式为矩形平板滑动阀门,舵机控制阀门滑动改变二次流入口面积,喷管单侧控制阀门总面积S0=0.5S1=0.088S。喷管上下结构关于XOZ平面完全对称。
该无源流体推力矢量喷管控制原理如图7所示,利用射流卷吸引射和Coanda附壁效应,通过控制阀门的开关闭合来控制射流方向偏转。当两侧控制阀门全开时,主射流的卷吸引射作用在二次流流入孔形成二次流,由外界大气进行补充,平衡腔体内部压力,射流能够保持中立稳定;当一侧阀门关闭后,由于主射流的卷吸引射作用,腔体内部气体被抽走后未能得到补充致使腔体内部压力急剧下降,形成低压区,同时喷管另一侧阀门最大面积开启,喷管两侧的压力差致使射流最大角度偏向一侧,射流附壁后保持稳定的偏转方向流动。

图7 无源流体推力矢量喷管射流偏转原理Fig.7 Jet deflection principle of passive fluid thrust vector nozzle
本文中采用的涡喷发动机尾排气截面为圆形,面积为S=1 385mm2,喷管截面为矩形。为尽可能减小推力损失,因此需要圆转矩形的过渡段进行型面过渡。过渡段结构参数如图8所示,其中D1为过渡段的射流入口直径,其对应的截面为射流入口,其直径等于发动机尾排气口直径,本文中D1=42 mm,D2为过渡段前唇口的直径,D2= 1.26D1。L1为前唇口到射流入口的距离,L1=0.4D1,L2为过渡段射流入口到射流出口的距离,L2=4D1。对于过渡段其射流入口与射流出口面积和发动机尾排气口面积S应保持相同。

图8 过渡段结构参数示意图Fig.8 Structural parameter diagram of transition section
本文中涡喷发动机采用Kingtech K60G 6 kg推力涡轮喷气发动机,涡喷发动机系统由发动机、发动机控制系统(ECU)、油泵供油系统和电源组成,发动机及线路连接如图9所示。本文实验中发动机保持额定工作状态,状态参数如表1所示。
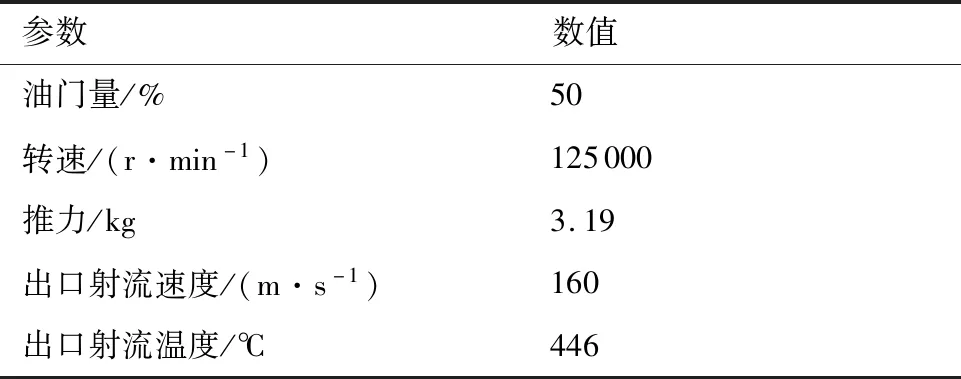
表1 实验中发动机状态Table 1 Experimental engine status

图9 涡喷发动机Fig.9 Turbojet engine
设计构建基于涡喷发动机的无源流体推力矢量实验台,如图10所示,其中喷管和过渡段均采用316L钢进行3D打印加工,满足高温高速射流的使用要求。考虑到原涡喷发动机尾喷管带有温度传感器进行温度测量,故本文实验中保留了涡喷发动机原装尾喷管,发动机尾喷管与过渡段采用同心非接触式的安装方式,中间留有流向距离为0.1D1的调压缝,用于PIV实验中示踪粒子的投放和引射外界气流辅助喷管散热。文中用“U-δU-D-δD”表示实验阀门状态,定义字母U代表上控制阀门,D代表下控制阀门,δ为阀门闭合度,δ=0表示阀门全开,δ=100%表示阀门全闭合。喷管阀门控制方式为:单独控制上阀门或下阀门,分别改变阀门开度δU或δD,令其从0~100%按12.5%步长变化,对应阀门闭合度值为0、12.5%、25%、37.5%、50%、62.5%、75%、87.5%、100%。文中在处理矢量角控制曲线中定义射流上偏矢量角为正,下偏矢量角为负,矢量角控制曲线横坐标阀门闭合度对应实验阀门状态如表2所示。

图10 基于涡喷发动机的无源流体推力矢量实验台Fig.10 Passive fluid thrust vector test bench based on turbojet engine

表2 实验阀门状态与横坐标阀门闭合度的对应关系Table 2 Correspondence between experimental valve status and abscissa
1.2 测试技术
1) 红外热成像
由于涡喷出口是高温射流,且带有未充分燃烧油粒子及燃烧后废弃物颗粒,故可以采用红外热成像仪红外拍摄来进行流动显示。本文中采用的设备是FLUKE公司的Ti400红外热像仪,该设备温度测量范围为-20°~+1 200°,热灵敏度<0.05 ℃,标准视场为24°×17°,空间分辨率为0.075°。实验选取拍摄截面为平行于射流流向的铅垂面(XOY面),红外热成像实验台示意图如图11所示。

图11 红外热成像实验台Fig.11 Infrared thermal imaging test bench
2) 粒子图像测速
使用粒子图像测速(PIV)系统对无源流体推力矢量喷管主射流静态偏转规律进行研究。实验中由于射流温度达到了466 ℃,示踪粒子使用粒径小(粒径约为0.2 μm)、易于分散、化学性质稳定的钛白粉(主要成分TiO2),PIV空间流场测量实验装置整体布局如图12(a)所示。激光片光平面平行于射流流向铅垂面(XOY面),CCD相机光轴与激光平面垂直。如图12(b)所示,PIV实验选取喷管中心对称面A作为拍摄截面。

图12 喷管射流流场PIV测量Fig.12 Nozzle jet flow field measurement with PIV
PIV采用丹麦Dantec公司系统产品,主要由双脉冲激光器、CCD相机、同步器、片光光学组件、粒子发生器和数据处理工作站等组成。双脉冲激光器输出波长为532 nm,每个脉冲输出能量为500 mJ。拍摄区域片光厚度小于1 mm;同步器的时钟分辨率小于0.5 μs;互相关CCD数字相机分辨率为2 048 pixel×2 048 pixel,拍摄频率为10 Hz。相机采集区域大小约为220 mm×220 mm,互相关查问域为16 pixel×16 pixel,每对图像计算得到128×128=16 384个速度矢量,所以每个速度矢量的空间分辨率为1.7 mm;PIV对流场速度的测量精度约为2%。
3) 推力矢量天平测力
将微型涡喷发动机-喷管实验台固定在六分量盒式天平上进行整体测力,如图13所示。盒式天平可以测得6个分量:分力FX、FY、FZ和力矩MX、MY、MZ。考虑到盒式天平FX、FY、FZ最大量程分别为5、15、5 kg,在设计制作涡喷-喷管实验台时做轻量化处理。完成后涡喷实验台整体重量约6 kg(FY≤15 kg),实验工况下发动机推力实测为2.58 kg(FX≤5 kg),满足天平量程使用要求。盒式天平技术指标如表3所示。
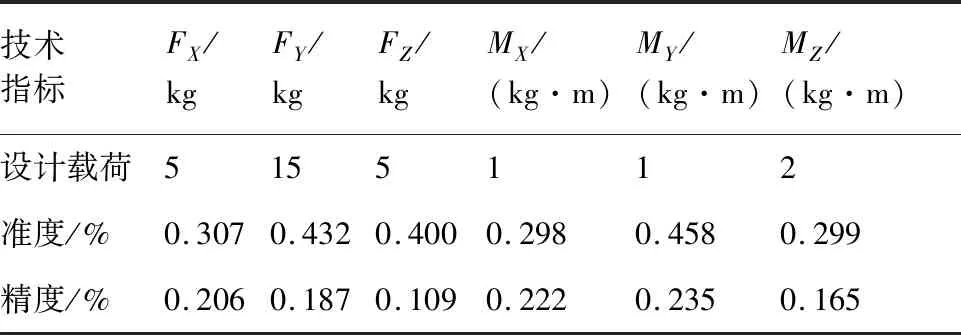
表3 盒式天平技术指标Table 3 Technical indicators of box type balance
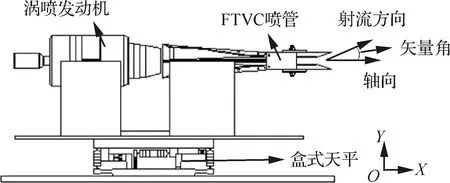
图13 推力矢量测力实验台Fig.13 Experimental platform for thrust vector force measurement
测力实验中应先对天平采集零点,然后再启动发动机,发动机稳定工作后,按照控制阀门闭合度值δ从0~100%以12.5%步长变化,天平进行同步测量采集。在阀门状态初始位置即U-0-D-0时,应当采集测力结果计算零点矢量角α0,考虑到模型装配可能存在误差导致发动机本身推力线和天平X方向不完全重合,故需要每个实验状态测量计算获得的推力矢量角都扣除矢量角基准零点值α0,从而消除模型装配带来的实验误差。
测力结果取天平测得的各个状态下X、Y方向的力FX、FY,由式(1)和式(2)计算可得各个状态的推力矢量角αT,最后绘制获得推力矢量角随二次流控制阀门变化的控制曲线。
α=arctan(FX/FY)
(1)
aT=α-α0
(2)
2 实验结果与分析
2.1 空间流场结果
1) 红外热成像
红外热成像作为一种流动显示的手段,可以清晰、直观显示主射流整体的偏转状态。本文首先通过红外热成像进行流动显示,初步了解主射流偏转特性。利用红外热成像仪显示每个阀门状态下主射流的流动状态,如图14所示。
由图14改变δ得到的主射流流动显示可知:当上下阀门全开时,射流中立稳定;随着控制阀门的闭合,主射流偏转角逐渐增大,当上阀门全关、下阀门全开时,射流最大角度上偏,当上阀门全开、下阀门全关时,射流最大角度下偏。
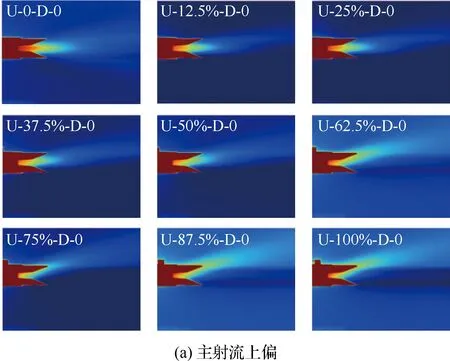
图14 红外热成像显示的射流偏转状态Fig.14 Jet deflection displayed by infrared thermal imaging
2) PIV实验结果
PIV实验中首先调整控制阀门,启动发动机,待到射流稳定后开始拍摄,拍摄时长10 s,获得100张粒子图。每个实验状态取50张粒子图做平均计算,获取A截面每个δ值下主射流偏转空间流场时均结果。对于射流中立(U-0-D-0)、射流最大角度上偏(U-100%-D-0)、射流最大角度下偏(U-0-D-100%)3个典型状态,其空间流场速度云图如图15所示。

图15 PIV实验A截面空间流场速度云图Fig.15 Velocity contours map of section A in PIV experiment
2.2 流动矢量角控制规律
研究者对流动矢量角的确定方法不一,一般有利用总压探针测压的速度型法、根据动量定理的流场法以及壁面压力法等。本文利用PIV实验获得的速度云图,计算射流的流动矢量角,以射流中立状态为例,计算过程为:


图16 流动偏转矢量角选取流线及计算点Fig.16 Selection of streamlines and points for jet deflect angle calculation
(3)
(4)
计算截面每个状态的流动矢量角,获得喷管的流动矢量角αF控制曲线,如图17所示,其中横坐标为控制阀门闭合度值。同时拟合出其线性控制方程和线性相关系数平方值R2,线性相关系数R的计算公式为

图17 流动矢量角随控制阀门变化曲线Fig.17 Variation curve of flow vector angles under valve’s control

(5)

可得流动矢量角线性控制方程及线性相关系数平方值为
αF=11.75δ-0.05
(6)
R2=0.99
(7)
由图17可以看出微型涡喷发动机热喷流条件下喷管最大流动矢量角为-12.3°/12.3°,控制规律曲线线性相关系数平方值为0.99,接近1,控制规律接近线性,不存在明显的主射流偏转突跳问题,可用拟合的线性控制方程αF=11.75δ-0.05近似表示该喷管的流动矢量角控制方程。
2.3 推力矢量角控制规律
通过盒式天平对矢量喷管进行4次重复性测力实验,结果如图18所示。将4次重复性实验得到的推力矢量角平均后获得平均推力矢量角随控制阀门变化的控制曲线,如图19所示。

图18 4次重复实验推力矢量角随控制阀门变化曲线Fig.18 Variation curves of thrust vector angles under valve’s control in four repetitive experiments

图19 平均推力矢量角随控制阀门变化曲线Fig.19 Variation curves of average thrust vector angle under valve’s control
可得推力矢量角线性控制方程及线性相关系数平方值为
αT=12.79δ+0.54
(8)
R2=0.98
(9)
由图18、图19可知,推力矢量控制4次重复性实验结果基本重合,表明该喷管在涡喷发动机的高速热喷流条件下具有多次可重复性的控制规律。最大推力矢量角为-12.9°/12.8°,控制规律曲线线性相关系数平方值为0.98,也接近于1,这表明该构型喷管在涡喷发动机动力下具有接近线性的推力矢量角控制规律,故可用拟合的线性方程αT=12.79δ+0.54作为推力矢量角控制规律的简化方程。
进一步对推力矢量角控制曲线进行多项式拟合,如图20所示,可得推力矢量角的多项式控制方程为

图20 推力矢量角随控制阀门变化曲线的多项式近似Fig.20 Polynomial approximation of variation curves of thrust vector angles under valve’s control
αT=5.76δ6-17.84δ5-12.50δ4+
25.02δ3+6.53δ2+5.53δ+0.11
(10)
R2=0.998 4
(11)
由图20可知,拟合的六次项方程曲线和推力矢量角控制曲线基本重合,其相关系数平方值达到了0.998 4,高于线性方程的0.98,更加接近于1,表明该六次项方程可以更加精确地表示推力矢量角的控制规律。
2.4 发动机总推力变化情况
流体推力矢量喷管在实现推力矢量化的同时,可能会影响发动机的工作状态,对发动机总推力产生一些影响。利用盒式天平4次重复性测力结果计算各个控制阀门状态下发动机的总推力TA,其计算表达式为
(12)
由式(12)计算获得发动机总推力随二次流控制阀门闭合度的变化情况,如图21所示。发动机尾喷流中立稳定不偏转时推力T0=2.58 kg。发动机总推力变化量为
(13)
图21结果表明无源流体推力矢量喷管的矢量控制对发动机工况和总推力影响不大,当发动机尾喷流向上/下偏转时,发动机总推力略有增大,由式(13) 计算得最大推力变化量为1.55%T0。分析其推力变化的原因可能是:射流偏转后推力损失更小;无源流体推力矢量喷管利用主射流的卷吸引射作用和Coanda附壁效应实现推力的矢量化,主射流卷吸引射外界大气形成控制矢量所需的二次流后,必会有一定的能量损失。由图7所示,射流中立,两侧形成稳定的二次流;射流偏转,单侧形成稳定的二次流,射流偏转后,因引射二次流而导致的能量损失更小,所以总推力会略有增大。

图21 发动机总推力随二次流控制阀门变化情况Fig.21 Variation of total thrust of engine with secondary flow valve
3 结 论
本文设计了新型的无源流体推力矢量喷管,构建了基于微型涡喷发动机热喷流条件下的无源流体推力矢量动力系统,通过红外热成像、PIV截面流场测量、推力矢量天平测力的实验手段对基于涡喷发动机的无源流体推力矢量喷管的控制规律展开研究,定量获得了涡喷发动机额定工作状态下该喷管的矢量角的控制规律。结果表明:
1) 在涡喷热喷流下,该无源流体推力矢量喷管可实现最大流动矢量角-12.3°/12.3°,最大推力矢量角-12.9°/12.8°。
2) 获得了推力矢量角控制方程。对推力矢量角控制规律拟合多项式方程,六次项方程曲线和推力矢量角控制曲线基本重合,其控制方程的相关系数平方值为R2=0.998 4,接近于1,表明该六次项方程可以精确表示推力矢量角的控制规律。
3) 获得了接近线性的矢量角控制规律。结果表明流动矢量角和推力矢量角控制规律相似、趋势相同,拟合线性控制方程的线性相关系数平方值都能达到0.98,表明该构型喷管在微型涡喷发动机热喷流下主射流连续可控偏转,并且具有接近线性的控制规律。
4) 获得了射流矢量偏转后发动机总推力的变化情况。发动机尾喷流矢量偏转后总推力最大变化量为1.55%T0,表明该构型喷管矢量控制对发动机工况影响较小。
本文研究结果表明该构型喷管在微型涡喷发动机作为动力时无明显的射流偏转突跳问题,具有接近线性的推力矢量角控制规律,符合飞行器控制的要求,能够为后续无源流体推力矢量技术涡喷验证机的设计试飞提供数据支撑和理论依据。后续仍须对该流体矢量喷管控制性能展开大量研究,其中包括推力损失、矢量动态响应、空间流场三维结构、Coanda壁面流动结构、喷管结构参数对矢量偏转规律的影响等。
