混沌Lur'e 系统的采样控制同步研究

赵韩笑 赵志伟 王嘉伟 葛 超

（1、华北理工大学 人工智能学院，河北 唐山063200 2、唐山学院 计算机科学与技术系，河北 唐山063000 3、华北理工大学 电气工程学院，河北 唐山063200）

CLS 同步问题的研究具有重要价值[1]。文献[2]通过构造适当的分段LKF，应用采样数据技术研究了具有时变时滞和不确定性的CLS 的鲁棒同步问题。文献[3]的作者考虑了CLS 的采样数据控制器的设计，该控制器采用采样时刻表示时间分段和基于自由矩阵的时变不连续LKF。文献[4]提出了一种新的基于采样数据反馈控制的延迟时钟同步的积分不等式方法。虽然已有许多研究成果被提出，但是，我们发现一些实际采样状态的重要的信息被忽略了，这也激发了本文研究的主要目的。

本文针对CLS 的主从同步问题，采用采样控制方法，提出了一种新的LKF，该方法能够充分利用系统的非线性特性，进而得到了低保守性的同步准则。仿真结果表明了该控制方法的有效性。

1 混沌Lur'e 系统的模型构建

2 主要结论

3 数值仿真

K 值如下：

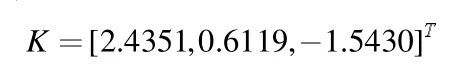
将结果与参考文献[7,8]进行比较，我们得到的h=0.6832 大于所列参考文献。因此，该方法比最近报道的方法更有效。

基于得到的K 值，给定系统初始值x（t）=[0.2 0.3 0.2]T，y（t）=[-0.3 -0.1 0.4]T。误差曲线如图1，从图中可以看出误差逐渐趋向于0。图2 为控制输入u（t）的响应曲线，显示了控制输入的时变离散特性。

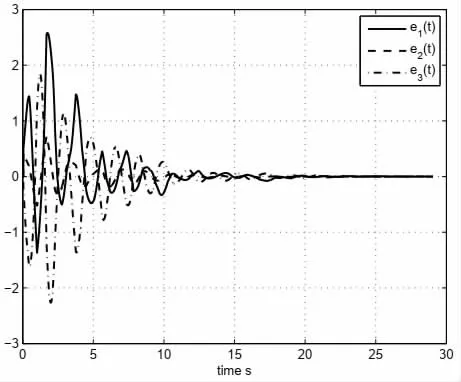
图1 误差系统曲线图

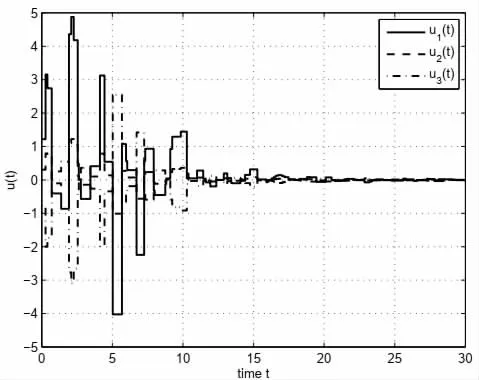
图2 u（t）的响应曲线图

4 结论

针对CLS 的同步，提出了一种新的随机采样数据控制方案。通过构造一个新的LKF 来保存更多关于实际采样模式特性的信息。利用改进的Wirtinger 不等式和互凸性方法，建立了主从系统同步的低保守性相关条件。此外，通过求解LMIs 得到采样控制器增益矩阵。通过算例分析，验证了本文方法的有效性。