基于碰撞预测的改进A*路径规划算法研究

陶 智 梁献霞 路俊维 赵 庆

（1、邢台职业技术学院信息工程系，河北 邢台054000 2、河北机电职业技术学院机电工程系，河北 邢台054000）

移动机器人的路径规划问题是当前移动机器人领域所研究的热点问题，其主要目标是在已知、未知或者部分未知的环境中规划出从起始点到目标点的安全无碰撞路径。

在已知的静态环境，所用的全局路径规划算法通常有栅格法、RRT 算法、A*算法、神经网络算法、遗传算法、蚁群算法等等。文献[1]改进A*算法中使用了正反向搜索的机制，范围仍然局限于静态障碍物环境下。对于动态障碍物环境下的路径规划，文献[2]采用了基本避障策略和启发式动态规划法相结合的思路，但是关于A*算法在动态障碍物下的路径规划研究文献却几乎空白[1-2]。

本文结合前人的研究成果，对动态障碍物环境下的路径规划进行研究探讨，在A*算法的基础上进行改进，通过引入逃逸距离策略解决机器人与动态障碍物相遇的问题，并对新算法进行了仿真验证。实验结果表明，采用逃逸距离策略后的算法，可提高机器人路径规划的安全效率。

1 栅格化网络

为了便于分析研究，将机器人、路径系统和障碍物进行网络栅格化处理，将不规则障碍物按照规则化处理，并设定路径网格的最小单位正方形，单位为1cm，如图1 所示。

图1 环境网格

2 A*算法引入

A*算法的评价函数表示为：f（n）=g（n）+h（n）。其中f（n）是从初始站点经由当前站点到目标站点的估计值，在寻路过程中，总是选择f（n）值最小的下一站点作为最优路径中的站点，g（n）表示从初始站点到当前站点已经付出的代价，h（n）表示从当前站点到目标站点的估计代价。

A*算法中g（n）值由起点开始所经过的距离累加而得，h（n）值则通过距离预估方法求得，通常有曼哈顿距离或者欧几里得距离[3-5]。

3 逃逸范围策略

实际情况下，移动障碍物的尺寸大于机器人尺寸，并且在相互运动过程中有冲突的可能，需要设置有效避障范围。预测机器人和动态障碍物相遇的边界，由此确定此时碰撞的矩形范围，机器人可以安全逃逸到达目标点，可以防止运行中被损坏。

3.1 最小矩形图

在实际环境中，障碍物有规则和不规则形状，为了方便处理，提出了最小矩形图的概念，即能够正好将整个障碍物包括在内的矩形，如图2 所示的障碍物都包含在长10cm 和宽为4cm 的矩形框内。

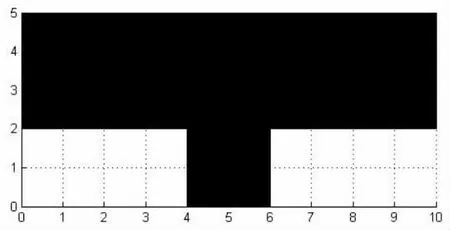
图2 中凸形障碍物

3.2 逃逸范围数学建模

假设机器人车体r，移动速度为vr，机器人坐标为r（rx, ry）。动态障碍物为o，运动速度为vo，障碍物的坐标为o（ox, oy），其横向长度为oh，纵向长度为ow，且在运动过程中不改变方向，机器人与障碍物的运动夹角为θ。

在没有遇到障碍物的情况下，机器人r 搜索路径的方向夹角为θ，因此机器人r 移动到障碍物o 边界的横向距离等同于纵向距离，可以推出此时机器人的坐标为（ox，ry+ox-rx），固逃逸范围是以（ox，ry+ox-rx）为坐标，横向长度为oh，纵向长度为ow的矩形。同理可以根据移动机器人r 和动态障碍物o 的相对位置和运动方向推出机器人r 移动到障碍物o 右边界和上下边界时的逃逸范围[6]。

3.3 逃逸范围计算模型

本文只考虑单动态障碍物的情况，对不规则的动态障碍物做了栅格化处理，统一为最小矩形图。机器人和障碍物在协同运动过程中可能同时占用路径网格资源[7-8]。图3、图4、图5 和图6 展示了在栅格型路径运动过程中可能出现的冲突类型。

当机器人移动到边界逃逸范围，即计算逃逸范围，其确定的方法，不同方向运动的计算各有差异，概括为四种情况，分别讨论如下[9-10]。

（1）机器人r 和障碍物o 右斜向相向运动

图3 右斜向相向运动逃逸

图4 左斜向相向运动逃逸

图5 左斜向反向运动逃逸

图6 右斜向反向运动逃逸

3.4 改进A*算法流程

引入逃逸范围策略，改进后A*算法的整体流程如图7 所示[11-12]。

其算法的流程可以简述为：

（1）加载路径网格坐标信息；

（2）判断有无障碍物，有则判断障碍物的状态，如果是动态，则执行改进A*算法，否则执行固有的A*算法；

（3）如果没有障碍物，则直接计算路径长度；

（4）更新机器人的坐标位置，并判断是否到达目的坐标，如果没有，则循环执行（2）、（3）和（4）步骤，否则，循环终止，流程结束。

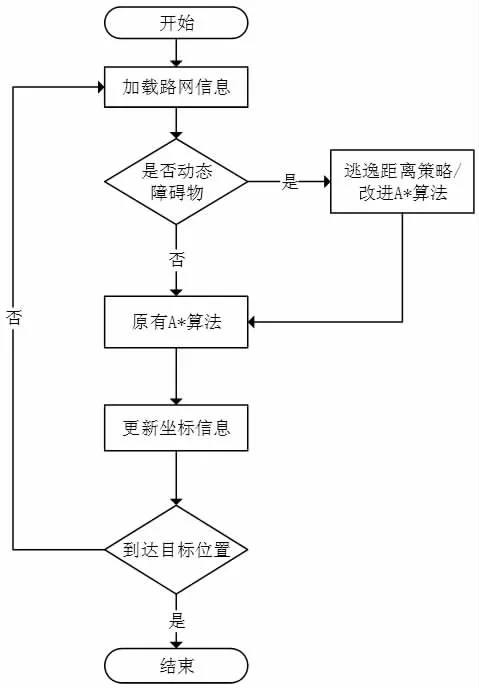
图7 路径规划算法流程

4 实验结果分析

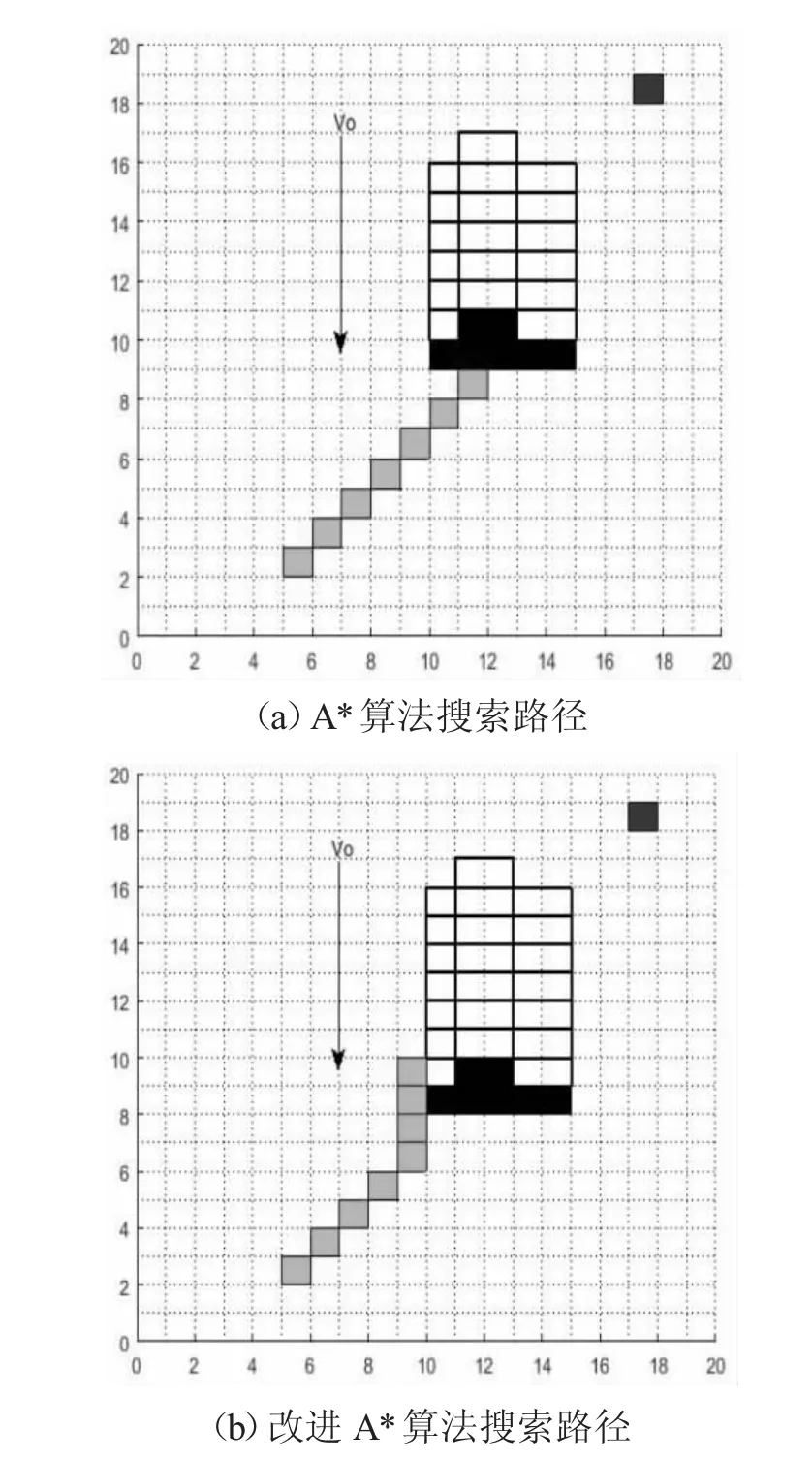
图8 斜向相向运动

不考虑障碍物之间的碰撞，且机器人和障碍物的移动速度均为匀速。网格中红色方框代表目标点，黑色边框代表动态障碍物的移动轨迹，黑色箭头表示障碍物的移动方向，绿色方框表示机器人的移动轨迹[13]。实验模拟对比了斜向相向运动情况下A*算法和改进A*算法后的情况，图8 中的（a）表示机器人r和障碍物o 刚好边界相遇的状态，（b）表示设置边界逃逸范围后的运动情况。

5 结论

通过改进A*算法，引入逃逸范围策略，通过对比仿真实验，证明此策略可以有效防止机器人与动态障碍物发生碰撞，避免了造成机器人的损伤，可以安全到达目标点。

本文探究了单动态障碍物下，机器人的路径规划，改进算法具有优越性，对于复杂环境中的多动态障碍物，以及多动态障碍物和静态障碍物同时存在的情况，将是下一步要研究的方向。